多重反射激光光杠杆测量金属线胀系数
2018-08-09骆泽如余观夏林杨帆
骆 敏,骆泽如,陈 蕾,余观夏,林杨帆
(1.南京林业大学 物理教学实验中心,江苏 南京 210037;2.南京市第一中学,江苏 南京 210001)
光杠杆原理在工程、材料、精密仪器等方面都有很多的应用[1-3],在大学物理实验中,常用光杠杆测量金属线胀系数[4-5]和杨氏模量[6-7]. 传统的光杠杆测量金属线胀系数涉及的仪器较多,光路调节复杂;占用空间较大,一般标尺和光杠杆平面镜之间的距离要1 m以上,测量中存在很大的误差. 针对这些问题,本文设计了多重反射光杠杆测量微位移系统,通过2个平面镜多次反射增大光程,从而进行微小变化量的放大,利用螺旋测微计来确定放大倍数.
1 实验原理
金属线胀系数是描述金属受热膨胀的重要参数,当固体温度升高时,由于分子的热运动,固体微粒间的距离增大,从而使固体膨胀. 因为一般物质的物理性质存在各向异性,为了准确研究物质某个方向的热膨胀性质,通常将固体做成该方向的一维线杆,在受热温度不太大时,固体在该方向长度变化是温度的线性函数,将这种现象叫固体的线膨胀,满足以下方程
Lt=L0(1+αt),
(1)
其中,L0表示物体在0 ℃时的长度,Lt表示物体在温度为t时的长度,α为固体线胀系数.
由于0 ℃时的长度不易获取,通常取2个任意的温度t1和ti,故式(1)中固体的线胀系数α又可表示为
(2)
式中L1表示固体在温度t1时的长度,ΔL为固体温度由t1升到ti时的伸长量.
1.1 传统光杠杆测量原理
如图1所示,传统光杠杆的测量原理为
(3)
其中,光杠杆的放大倍数为N=2D/b,xi和x1分别为温度ti和t1是对应标尺的读数.
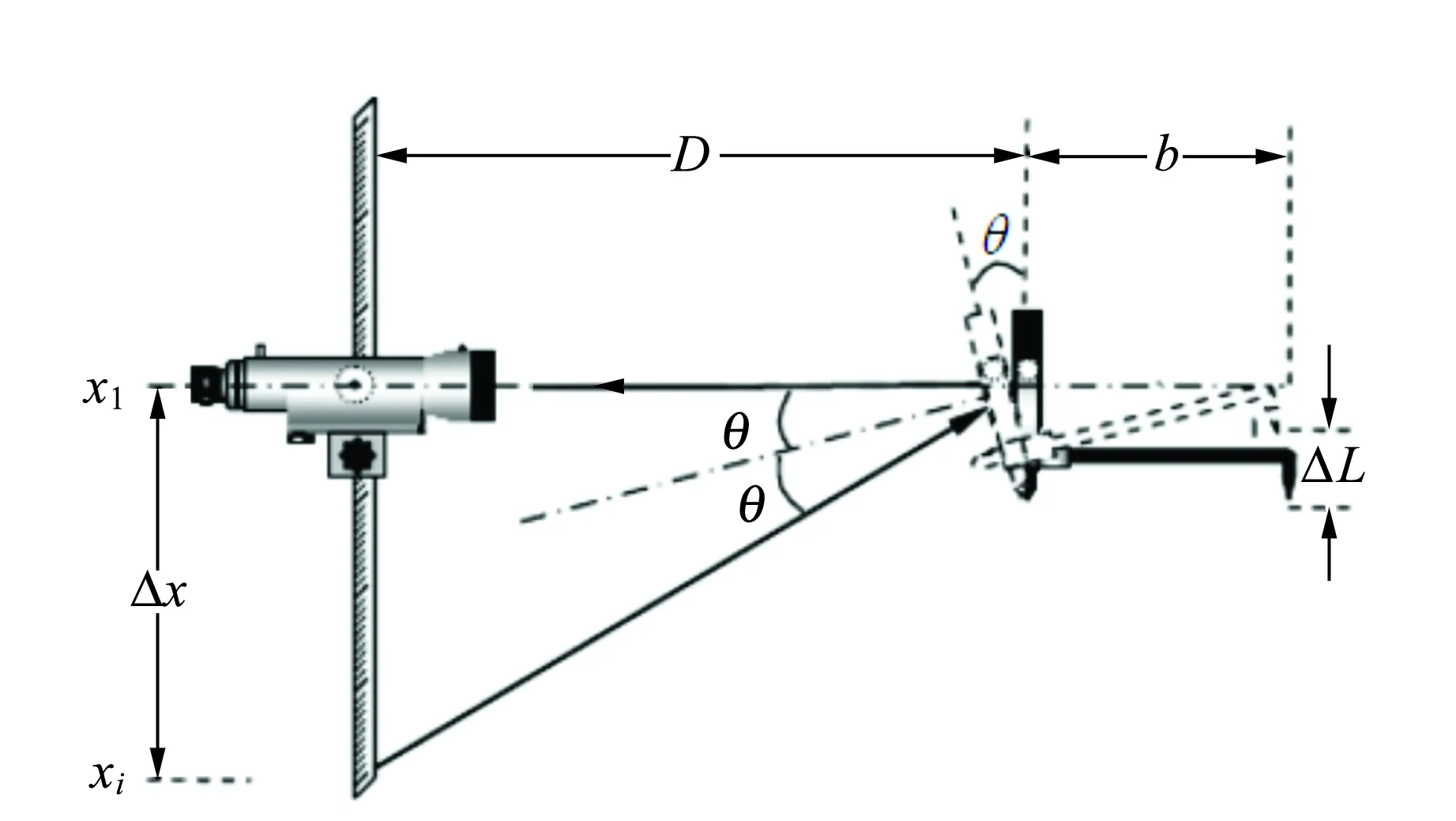
图1 传统光杠杆测量原理图
由式(2)~(3)可得
xi=αNL1ti+x1-αNL1t1=Kti+C,
(4)
其中,斜率K=αNL1,截距C=x1-αNL1. 实验测出多组数据(ti,xi),通过作图求出斜率K,由此得到金属线胀系数为
(5)
1.2 多重反射光杠杆的放大倍数
如图2所示,激光入射角度为θ0(小角度),当光杠杆没有发生微小变化时,1~3次反射后对应的观察点位置分别为x1,x2,x3,当光杠杆微小变化ΔL,偏转小角度为θ时,此时1~3次反射后观察点位置分别变化为x1′,x2′,x3′,则反射1次观察点位置对应的变化量为

图2 多重反射光杠杆放大原理图
x1′-x1=Dtan (2θ+θ0)+Dtanθ0-2Dtanθ0=2D×θ,
(6)
反射2次观察点位置对应的变化量为
x2′-x2=Dtan (4θ+θ0)+
Dtan (2θ+θ0)+Dtan (2θ+θ0)+
Dtanθ0-4Dtanθ0=2D×4θ,
(7)
反射3次观察点位置对应的变化量为
x3′-x3=Dtan (6θ+θ0)+Dtan (4θ+θ0)+
Dtan (4θ+θ0)+Dtan (2θ+θ0)+
Dtan (2θ+θ0)+Dtanθ0-
6Dtanθ0=2D×9θ.
(8)
由式(6)~(8)可推导得,n次反射观察点位置对应的变化量为
xn′-xn=2Dn2θ,
(9)
其中θ=ΔL/b,由式(9)可得
(10)
则放大倍数为
(11)
根据式(10),为了更好地保证多次反射后观察点位置的变化量(xn′-xn)和铜棒伸长量(ΔL)的关系是线性的,测量时保持反射次数n不变,本文测量保持n=3.
1.3 多重反射光杠杆测量原理
光杠杆原理利用光线的反射定律将微小位移放大,通过测量放大量和放大倍数间接测量微小变化量. 多重反射激光光杠杆的方法为:1)用2个相同的平面反射镜A和B代替传统光杠杆中的平面镜增加光在传播过程中反射次数,提高放大倍数;2)通过螺旋测微计确定放大倍数.
实验测量装置如图3所示. 光学放大的核心由2个平面镜A和B组成,平面镜B固定,平面镜A可动,动镜A前足尖放在被测铜杆的顶端,后足尖放在螺旋测微计平移台上面. 激光发射器发出的激光经过2个平面镜之间的多次反射,由平面镜A照射到标尺上面. 当被测铜杆受热变化微小位移时,前足尖带动动镜A偏转微小角度,由平面镜A照射在标尺上的激光相应地会产生较大位移量. 同时可通过调整激光的入射角度或平面镜长度,增加光束在2个平面镜间的反射次数,从而增大光杠杆的放大倍数. 在加热测量前,通过调节螺旋测微计读出使动镜A升高或者降低微小位移d,同时记录激光在标尺上的前后读数差ΔD,从而直接确定放大倍数N=ΔD/d.

图3 实验装置示意图
2 实验数据及处理
2.1 铜杆长度的数据处理
使用50分度的游标卡尺多次测量被测铜杆的长度,见表1.

表1 室温下铜杆长度测量数据 mm
经计算得铜杆长度L为
L=(496.41±0.02) mm.
2.2 放大倍数确定和数据处理
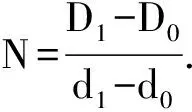
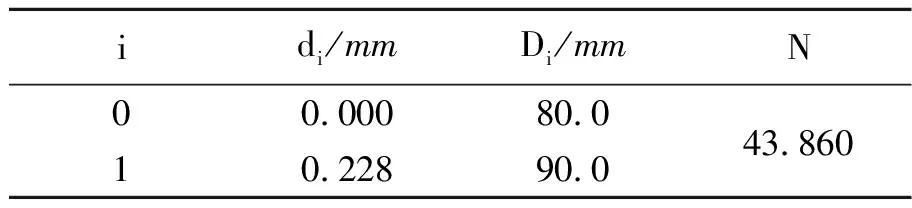
表2 放大倍数测量
采用标尺和螺旋测微计的最小分度分别为0.5 mm和0.01 mm,则标尺的Δ仪=0.25 mm,螺旋测微计的Δ仪=0.005 mm. 由此可得
u(d1-d0)=0.004 mm,
u(D1-D0)=0.204 mm,
则放大倍数间接不确定度为
u(N)=1.2,
放大倍数为N=43.9±1.2.
2.3 标尺读数
采用降温方式测量[8],将被测铜杆加热到105 ℃停止加热,让铜杆自然降温,记录降温过程中温度为85,80,75,70,65,60,55,50,45,40 ℃,激光分别对应标尺上的读数xi,见表3.

表3 降温测量的实验数据
2.4 金属线胀系数计算
根据表3的数据通过Origin作图拟合曲线如图4所示,得出斜率为K=0.383±0.002 mm/℃,则测量结果为
α=(1.76±0.05)×10-5/℃.
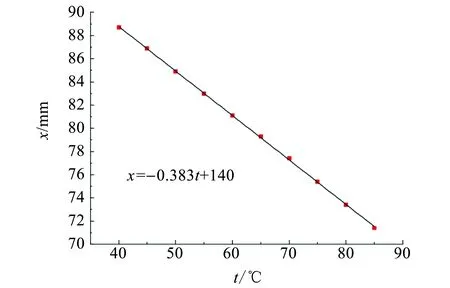
图4 数据线性拟合图
3 结束语
通过测量结果可知,该光杠杆测量系统可以满足实验的测量要求. 在保留光杠杆测量微小量的放大作用的同时,使待测物理量减少和降低产生误差的因素,使实验原理和现象更加直观,操作简单,节省实验时间. 利用平面镜和激光器代替望远镜,降低实验仪器成本,占用空间减小.
