基于网络连接及服务中心选择的高铁路网区域划分方法

张强锋, 王恪铭, 倪少权，吕红霞

(1.西南交通大学 交通运输与物流学院，四川 成都 610031；2.西南交通大学 信息科学与技术学院，四川 峨眉山 614202)

近年来我国高铁线网规模跃居世界第一，全国性的高铁路网日益完善，区域内高铁线路的网络化正在形成。在高铁客运需求大幅增长、部分高铁线路运力紧张趋势加剧的背景下，我国高铁运输产品有了在区域内公交化开行、跨区域范围提升直达旅行比例及换乘便捷程度等更高的设计要求。随着改革纵深的推进，区域铁路公司的市场主体地位进一步确定。为了适应高铁的特点和铁路的发展，亟待进行高铁最佳管辖区域的研究，以编制出符合区域协同优化要求的高铁运行图，增强区域性铁路公司的经营自主性，满足新时代我国高铁运输的发展变化要求，而合理地进行高铁路网的区域划分是解决这一难题的基础。

目前已有不少学者进行了运输区域划分相关问题的研究。袁长伟等[1]的研究中关注了公路运输区域的等级划分问题，而路网区域划分问题需要进一步考虑路网的连接性；刘伟铭 等[2]使用聚类分析方法对高速公路最佳运营区域划分问题进行了研究，且考虑了区域连接性的指标；在铁路区域的划分问题中，PITTMAN[3]研究了中国货运铁路划分的风险规避问题；KOPICKI与THOMPSON等[4]，NILSSON[5]，MIZUTANI与NAKAMURA[6]，PITTMAN[7]从政策与财务的角度，研究了铁路公司的划分与重组问题；莫辉辉与王姣娥[8]基于功能区的网络分析方法研究了中国货物路网区域的划分问题，但缺少定量的划分决策模型；孙有霞[9]使用聚类方法对中国铁路区域进行了划分，由于聚类划分方法只适合于分类问题，无法保证同一划分区域的连接性，需要事后对分类结果进行调整。目前对运输区域划分问题的研究仍较少，且存在未考虑区域中心的选择及路网区域的连接性、忽略最佳服务距离及网络均衡性等缺陷，缺少可以进行定量决策的模型化研究成果。

本文针对以上研究现状，基于高铁区域内的路网连结特性与区域中心点的特征，并体现高铁区域划分依据的约束要求，以区域内路网节点与服务中心的距离及连接紧密度为目标，以服务半径、服务容量约束划分后的子区域规模，建立了高铁区域路网划分决策优化模型。基于多目标转化方法，设计了一种向量编码的遗传算法进行求解。最后，以中国铁路总公司管辖路网区域构建算例进行计算，提出了高铁转运量折算方法，通过对比聚类算法的缺陷，说明了本文模型与算法的适应性与灵活性，并分析目标权重系数、服务半径系数、服务容量系数等参数对划分结果的影响，测试得出了服务半径系数、服务容量系数的设定方法。

1 问题描述

1.1 高铁区域路网划分因素

在高铁区域路网划分问题中，不能将区域的重心直接确定为区域路网内的中心点。为满足区域内与区域间的动车开行需要，区域路网内的中心点除了具有较强的动车储备与检修能力，还应与区域内各个地区(节点)连接距离较短，并与各个节点有较好的连通性，且区域划分范围应考虑高铁最佳管理距离的要求。此外，为了保持各个子区域服务能力的均衡性，应对子区域的最大服务能力进行约束；且为了突出各个子区域内部的网络特性，区域内的各个地区(节点)之间应具有较好的连接度。可见，在考虑以上约束的前提下，需要决策的问题有：哪些最小地区单元同属一个子区域；划分后的子区域中，选择哪个地区的路网中心作为该子区域的服务中心。

1.2 模型假设

建模之前，为清晰描述，做如下假设。

(1) 区域划分的数量由决策者根据相关发展规划给定。在网络图中，最小划分单元用该单元的网络中心点表示。

(2) 划分后的区域路网服务中心应在动车储备与检修能力最强的最小地区单元。采用动车所的检查库线与存车线数量之和代表动车储备与检修能力。

(3) 通过区域服务半径与服务容量约束限制区域划分规模。即区域服务中心与区域内各单元中心点之间的距离应满足最大服务半径的要求，划分后区域的服务容量之和不高于服务容量约束。用区域内的高铁客运总周转量表示其服务容量。

(4) 除区域服务中心与同一区域各个地区路网中心节点之间的距离之和越小这一指标外，另采用区域内各节点之间高铁线路连接的数量之和与区域内的节点总数之比表示该区域的网络连通度，该值越大表示区域内的网络连接程度越好。

2 决策优化模型

2.1 符号说明

1)参数

G=G(V,E)为整个路网的集合，其中V为路网中节点(最小划分单元的网络中心点)的集合，V={v1,v2,…，vn}；E为节点之间的高铁线路，即路网中的边，E={eij|i=1,2,…n;j=1,2,…n}，其中n为节点总数。

rij：节点vi与vj之间的高铁线路连接数量，即边的数量，rij=|∑eij|， ∀i,j∈V。

Dij：vi与vj之间的距离，∀i,j∈V。

xi,yi：vi的横、纵坐标，∀i∈V。

Ui：vi所辖区域的动车储备与检修能力，∀i∈V。

Pi：vi所辖区域的年高铁客运总周转量，∀i∈V。

Dv：铁路平均运距。

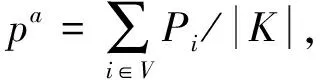
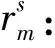
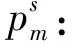
2)中间变量

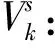
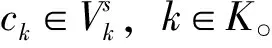
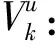
3)决策变量

aik：0-1变量，vi属于子图(区域)k时aik为1，否则为0，∀i∈V,k∈K。

hik：0-1变量，vi为子图(区域)k的中心节点时hik为1，否则为0，∀i∈V,k∈K。

2.2 模型建立

(1)

(2)

s.t.

(3)

(4)

(5)

∀j∈Vdk},∀k∈K

(6)

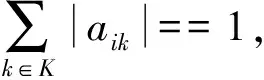
(7)

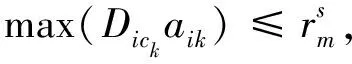
(8)

(9)

Dij=fun(xi,yi,xj,yj),∀i,j∈V

(10)

aik,cik∈{0,1}, ∀i∈V,k∈K

(11)

目标函数中：式(1)是使各个子区域内中心点距离其他点之和最小化，式(2)是使各区域内的网络连通度之和最大化。约束条件中：式(3)是子区域中心点的定义，式(4)为子区域中心点决策变量约束，式(5)为子图各节点的集合，式(6)表示子图中动车储备与检修能力最强的节点，式(7)为1个节点只能属于1个子图的约束，式(8)为子图中心点的服务半径约束，式(9)为子图中心点的服务容量约束，式(10)为两节点之间距离函数的表达式，式(11)为决策变量的值域约束。

3 模型求解

3.1 多目标转化

上述模型是一个多目标优化问题，引进目标值权重系数ω1，ω2，且ω1+ω2=1，将上述模型转化成单目标问题模型，即

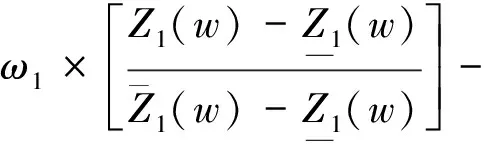
(12)

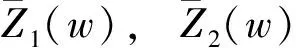
3.2 向量编码遗传优化算法

上述模型是一个混合整数规划模型，属于NP-hard问题。为此，文中设计了一种遗传算法进行求解。针对研究问题的特点，算法编码采用了向量的形式[10]，即直接以编码中的各基因值(Allele值)对应相应的路网节点编号，采用编码中前段|K|个基因代表候选区域中心点，即字串1，剩余编码为字串2，即各个候选节点。此向量方式的编码与解码过程较为简捷，但编码长度增加，交叉、变异时的处理时间相应增长，运算时占用更多的存储空间，但相对于目前大容量的计算机内存及较快的处理速度可忽略不计，不失为解决本文特定问题的一种有效方法。

编码与解码示意图如图1所示。其中，可行解的产生过程如下：通过计算各个候选节点与各个候选中心点的区域松散值，即按式(12)计算两点之间距离与连通度对应的目标函数值，根据计算结果进行排序，分配各个候选节点至与其有最小区域松散值的候选中心点；按区域内各点的Ui值调整得出新的中心点；按最大服务半径约束检查区域内各个节点，通过对超出约束的节点至其他中心点的区域松散值从小到大排序，确定候选接收区域顺序，将超出约束的节点调整至候选接收区域接纳后，仍可满足服务半径与服务容量约束的候选接收区域中；按最大服务容量约束检查各个区域，在不满足容量的区域内，将与其他节点聚合性最差的节点依次标记为超出约束节点，按上述超出距离约束节点的调整方法，将这些节点调整至合适区域中，直到该区域的容量约束得到满足为止。模型求解过程如下。

Step 1：令遗传进化代数g=0，设置最大进化代数gm。根据向量编码规则，按元素编号生成q个初始种群。

Step 2：按解码规则遍历当前种群每条染色体l的基因位，计算得出各个中心点所属的各节点，按距离与容量约束调整各个子区域大小，并重新计算调整得出中心点，形成可行的区域划分方案。

Step 3：计算每条染色体l的适应度函数值F(l)=(1 000/Z(l))2，Z(l)为第l条染色体的目标值，按式(12)计算，l=1,2,…,q。

图1 编码与解码示意图

Step 4：使用轮盘赌策略选择染色体，进行遗传进化操作，生成临时种群。

对各条染色体进行交叉、变异操作：按交叉率Pc进行单点交叉与部分匹配交叉，按变异率Pm进行逆转变异。

Step 5：采用精英保留策略从当前种群中选择部分染色体，结合临时种群生成下一代的种群。

Step 6：若g≤gm，g=g+1，转至Step 2；否则，以进化过程中求得到的具有最大适应度个体所对应的区域划分方案为最优方案。

4 算例分析

4.1 算例构建

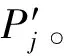
(13)

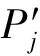
(14)

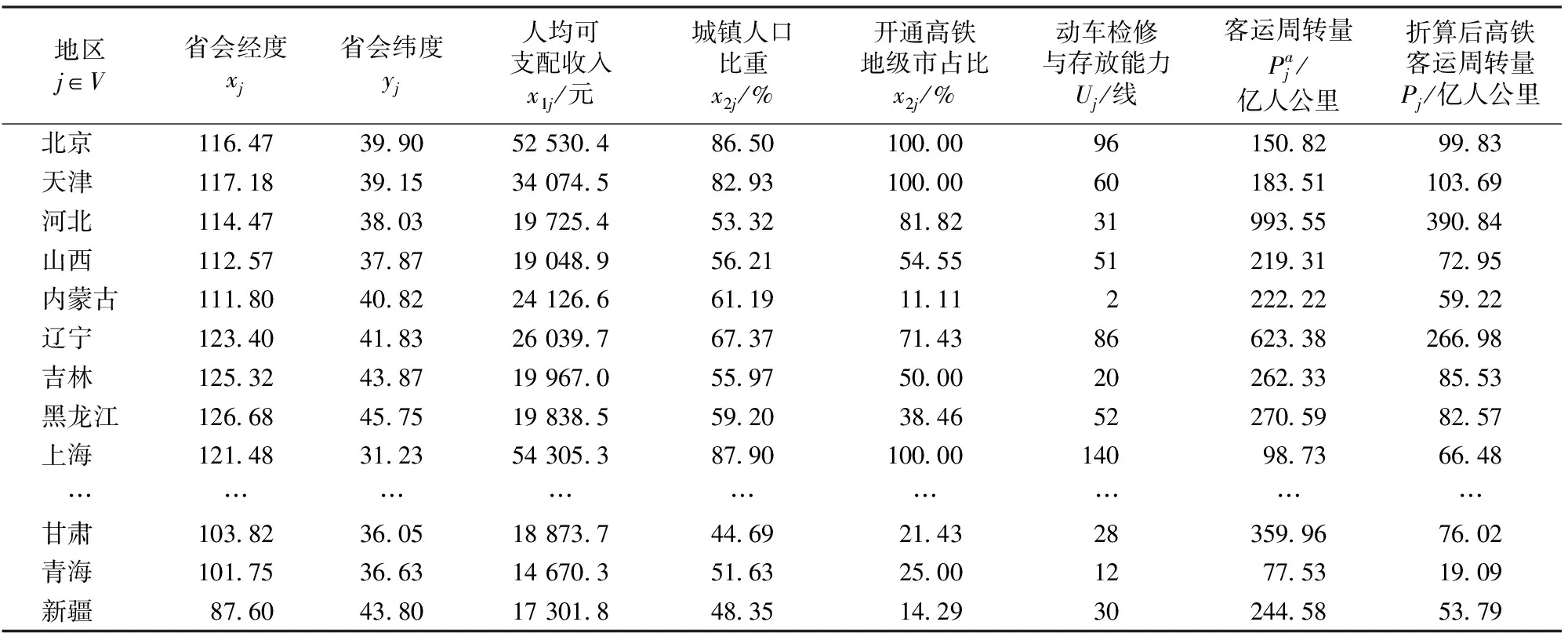
表1 各地区的分析统计数据

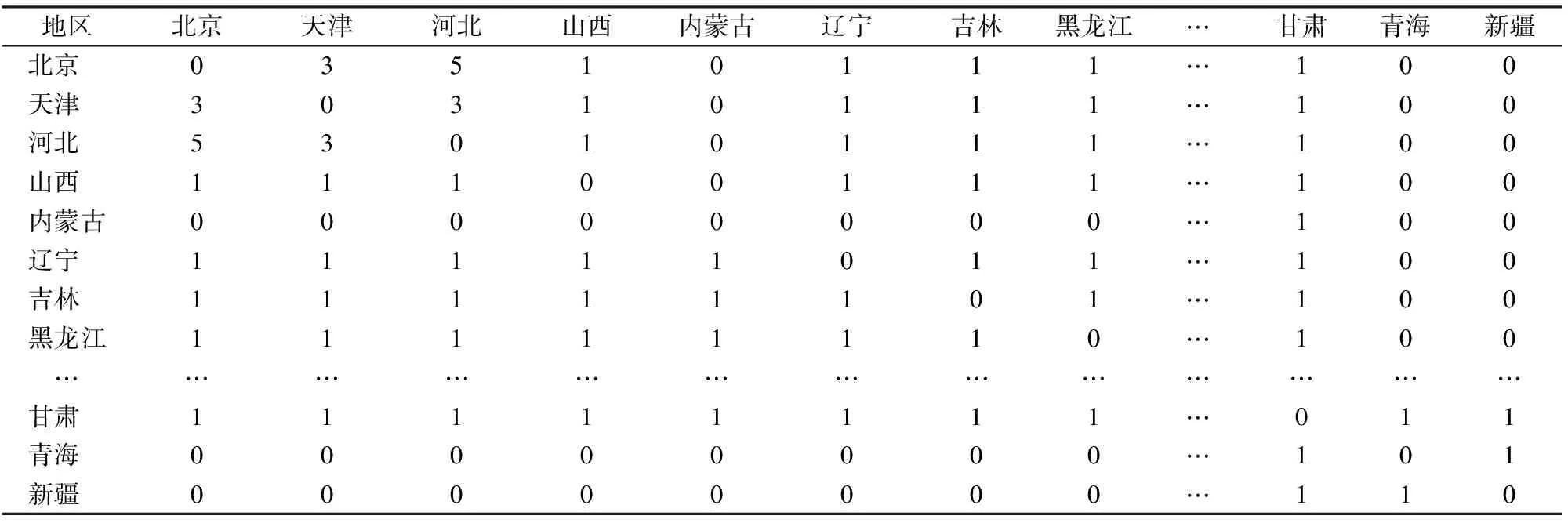
表2 各地区之间的高铁路网连通度

其他参数设置如下：gm=1 000，Pc=0.7，Pm=0.7，q=100。取ω1=0.5，ω2=0.5，|K|=7。其中，2017统计年鉴得出的铁路平均运距Dv为447 km，另外取α=2，β=2。采用Matlab R2017a编程实现上述算法，在inter CORE i7+7700CPU，16G内存的微机上对测试算例进行了求解，计算时间约为160 s，目标函数值的收敛情况如图2所示。

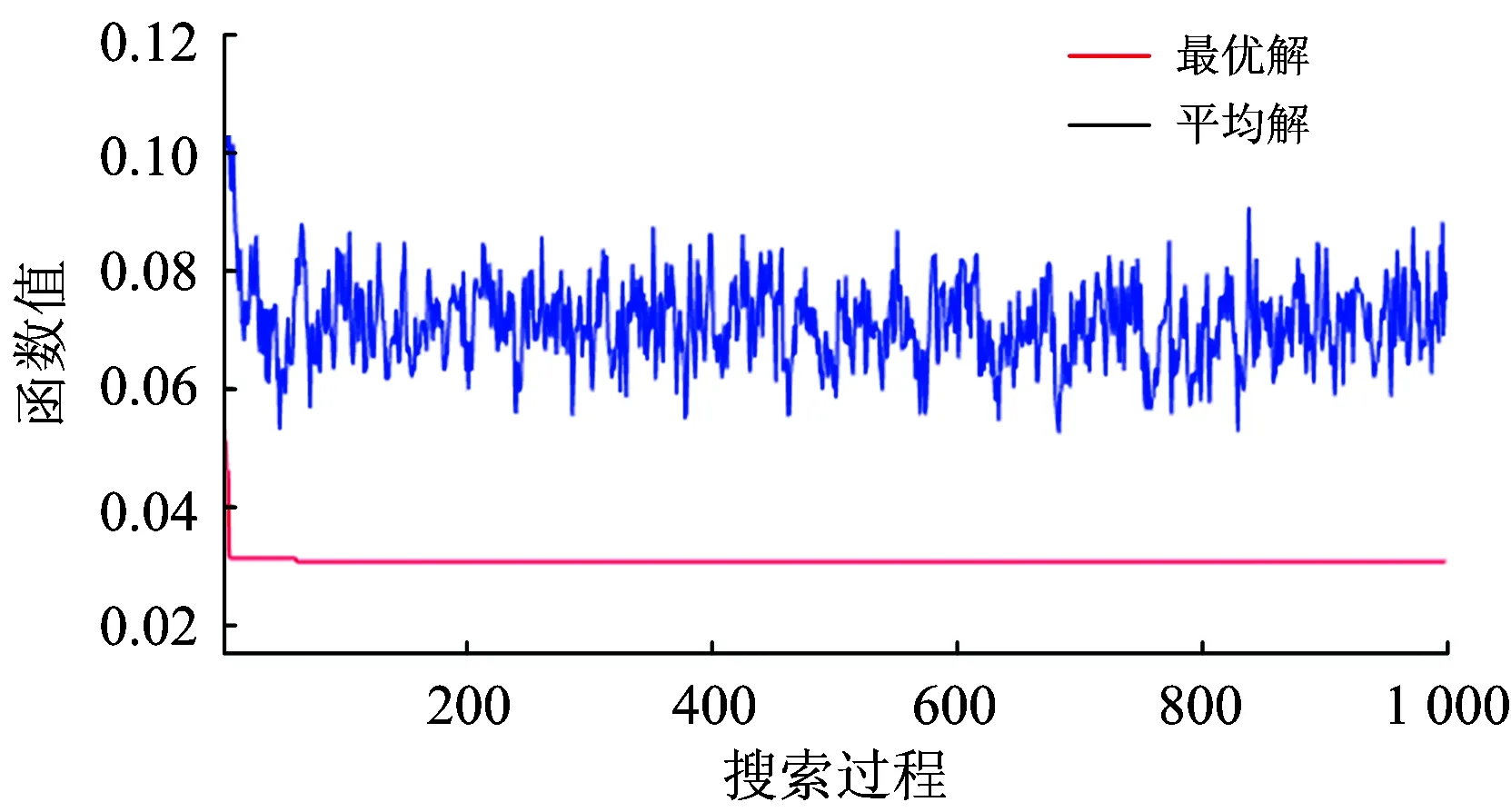
图2 目标函数值的收敛情况

表3为本文模型算法的划分方案，其中“★”为中心点。本文研究中同时使用聚类算法进行的一系列测试计算发现：层次聚类算法的结果依赖于之前层次的划分方案，无法证实当前层次划分结果为最优解；K均值聚类算法的结果对初始中心值的选择非常敏感[12]，导致各次计算结果不一致，得到最优解有一定的随机性，算法的稳定性差。这些聚类算法只能输入相互独立的指标参数，适用于常规的分类问题。该类算法无法处理网络相关问题，输入多个指标进行聚类的结果没有网络连接性，得不出可行解，且该算法缺少调节性参数。本文模型算法解决了一个比分类问题的复杂度更高的网络划分问题，且通过改变参数(如服务半径与容量约束、目标函数权重等)，该模型算法可以得到更多适应性的划分方案，体现了较好的灵活性。

表3 基于路网连接及中心点选择的划分结果

表4为仅输入距离参数的|K|均值聚类算法得出的划分方案，其中各区域的中心为该区域的重心。对比表3分析如下。

(1) 路网邻域连接影响了区域划分结果。在表4仅考虑距离这一个目标的划分方案中，区域中心是该区域的重心，各节点与该中心点团簇构成各个子区域。为了最小化区域内距离，表4中贵州与四川为一个区域，而在表3中综合考虑了路网邻域连接(贵广高铁)，贵州与广东划分在同一区域。同理，因为路网的连接性(郑西高铁)，陕西也与河南划分在同一区域中。

(2) 中心点的选择也对区域划分造成了影响。在表3中，中心点的选择与动车储备与检修能力相关，如因有较强的动车服务能力，在子区域靠外围位置的北京、上海被调整为区域的中心点。

(3) 最大服务半径与服务容量约束影响划分结果。由于服务容量的约束，对比表4发现，表3中北京、上海两节点所在的区域范围减小。在表3中，湖北与中心点陕西的距离最近，其次是上海。若湖北被划入陕西的省会为中心的所在区域，由于湖北的动车储备与检修能力较大，湖北的省会会被调整成为该区域的中心，增大了目标函数值，且造成湖北的省会与青海的省会两点之间不满足服务半径约束；由于容量约束的限制，湖北也不会被划分到上海所在区域中，而是被划入与其连接度较好的中心点为广东省会所在的区域中。

表4仅输入距离参数的划分结果(|K|均值聚类算法)

区域编号区域所辖的地区1黑龙江,吉林,辽宁2内蒙古,山西,河北,河南,山东,天津,北京3湖北,湖南,江苏,安徽,江西,福建,浙江,上海4广西,海南,广东5云南,重庆,贵州,四川6青海,甘肃,陕西7新疆

4.2 参数敏感性分析

通过式(12)对各个目标函数的权重系数进行设置，可以得出更多体现决策偏好的参考划分方案。当设置距离权重系数ω1与区域内连接度权重系数ω2均为0.5时，最优目标函数值约等于0。当ω1=0.59，ω2=0.41时，计算得出的最优划分方案对比表3产生的变化为：贵州被划入距离其较近的中心节点为四川的省会所在的区域中。当ω1=1.0，ω2=0时，该模型将退化成一个带服务半径与服务容量约束的最小化区域内连接距离的单目标模型，青海、甘肃与云南、重庆都被划入了以四川的省会为中心点的区域中，陕西、河南、湖南、江西划入以湖北的省会为中心的区域中，区域内部的连通性均下降。当ω1=0.7，ω2=0.3时得出的计算结果仍与表3相同。而当ω1=0，ω2=1.0时，该模型将退化成一个最大化区域内连接度的单目标模型，计算得出的区域划分方案中，由于路网的疏密程度导致求解方案中的以北京、上海、广东的省会为中心的区域划分过大，各子区域之间的均衡性下降。该测试结果说明：目标函数的权重系数选取需要体现决策偏好，应综合距离与连接度指标，设置适当目标权重，以得出合理划分方案。

模型中通过设置最大服务半径与最大服务容量约束以调节划分方案中各个区域的均衡性，可见这两个约束的设定值会影响划分结果。保持其他参数与表3相同，改变半径系数α、容量系数β的值，测试得出不同约束条件下子区域的最大节点数量及最优目标函数的变化，如表5所示。“/”表示无解或无对比，α=1时，无法计算得出1～7个子区域的划分方案，当取β=1时也无法得出划分方案。以表中α=3，β=4时的值“7，-，↓”为例，表示此时得出的最优方案中，子区域包含的最大节点为7个，目标函数值与左前表格中即α=3，β=3时的值对比没有变化，但与上前方表格即α=2，β=4时的值对比减小。

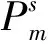
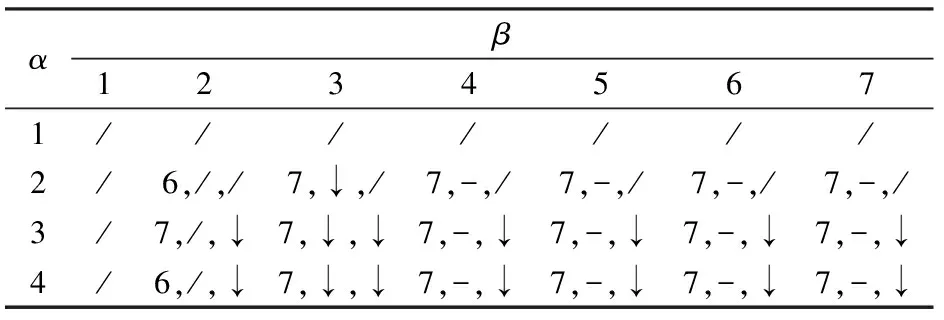
表5 不同约束条件下子区域的最大节点数量及目标函数值的变化

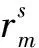
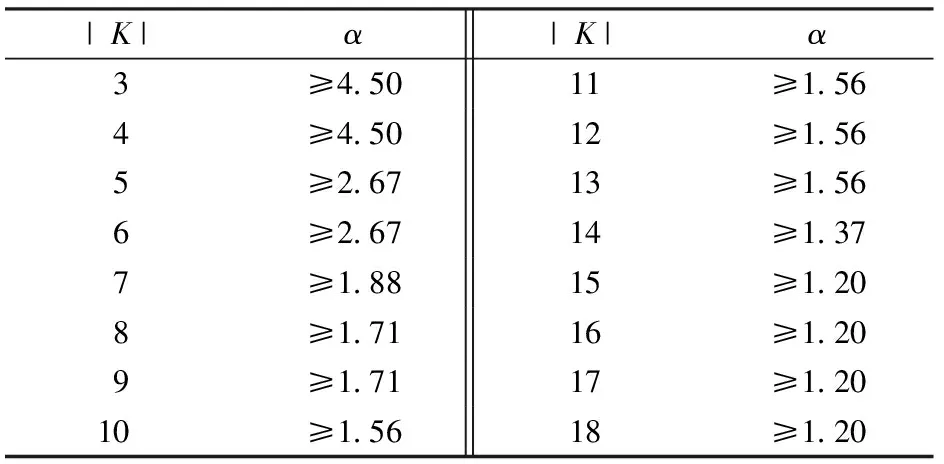
表6 不同划分数量下的半径系数取值

5 结 论

针对目前国内外研究中对铁路区域划分尚无模型化研究成果这一难题，本文提出了一种决策方法：结合路网邻接特性，并考虑动车储备与维修能力进行区域中心的选择，以最小连接距离、最大路网平均连接度为目标，建立了高铁路网区域划分混合整数规划模型，设计了一种向量编码方式的遗传优化算法进行求解，提出了高铁客运周转量折算的方法，并以中国铁路总公司所属路网区域构建算例，对模型与算法进行了验证。结果表明：

(1) 模型和算法可以有效解决高铁路网区域划分问题，划分方案体现了高铁网络连接特性与动车服务水平。基于路网邻域连接及中心点选择的划分方案较强的适应性与灵活性，解决了均值聚类算法无法处理路网参数及稳定性差的问题，提高了最优解的求解能力，避免了仅考虑距离或连接度单一指标的划分缺陷。

(2) 应当综合调整距离目标与连接度目标的权重，计算得出符合决策者偏好的划分方案。且需要设置适当的最大服务半径与服务容量参数，以约束划分方案的均衡性。在给定区域划分数量时，最大服务半径的取值有下限要求；较小的最大服务容量约束也会导致无法得出可行解，且最大服务容量超出平均区域服务容量的一定倍数时，该约束失效。

目前在全国范围内我国高铁线路尚没有形成较强的网络特性，因此未来的研究包括：考虑以未来建成的中长期高铁规划路网为划分对象；研究合理区域划分数量的确定方法等。