基于神经网络的冗余机械臂运动学逆解研究分析

张博

（宝鸡文理学院陕西宝鸡721016）

通常情况下，工业机器人的自由度为6个，实践经验发现自由度的增加可以使工业机器人的性能得到显著改善，比如可以实现避障、灵活度增加以及机械臂性能的改善等，在带来便利性的同时，也增加了运动学逆解[1-3]。关于这项问题的研究也是一项重要的内容，主要是通过求解复杂过程辨别矩阵违逆[4]。如果是采用传统的方法无法满足实时控制冗余机械臂的要求[5-6]。人工神经功能对于非线性系统的逼近能力十分强大，以神经网络为基础的相关方法也已经被成功引入到了冗余机械臂的实际求解过程中[7]。

为了使机械臂的应用方便性以及控制精度等得到强化与提升，本次所采用的王法为RBF神经网络，然后再借助于遗传算法来完成运动学逆解，最终对设计的内容开展相应的仿真实验，验证其应用效果。

1 构建方程

本次研究所采用的建模方法为D-H模型，这种模型对于机器人的关节和连杆建模都十分方便，对于机器人中的两个相邻连杆坐标系的空间位姿关系采用齐次变换矩阵展开相应的描述。本次研究主要是对于冗余机械臂展开研究，所以也可以采用D-H建模方法。根据该模型的建模规则，所建立的机械臂坐标系如图1所示。

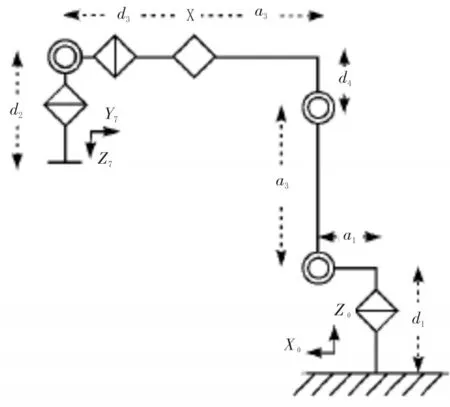
图1 机械臂坐标系示意图

图1为机械臂所建立的坐标系，从坐标系可以得到相关的模型参数表：

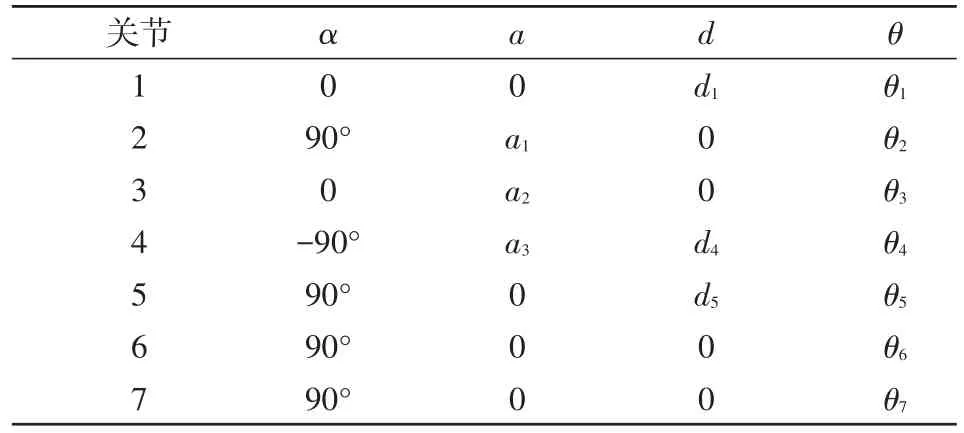
表1 模型具体参数

2 详细设计

2.1 建立适应度函数

正运动学所有的方程当中共包含12个，其中一半的方程属于独立方程[8]。在机械臂采用证运动学方程进行解算的过程中，因为受到冗余自由度的影响，会导致出现无穷多的运动学逆解，想要使这么多的逆解当中获取唯一的一个逆解，就必须要再额外的附加其他的条件，最终得到最优解[9-10]。本次研究当中采用了最佳柔顺性的相关规则，这种规则应用的前提是加权最小二乘法。需要对方程的条件增加约束条件，通过约束条件的添加，可以得到最优的逆解。关于本规则的表达式如下：

在以上公式当中，关节i自身所处位置的关节角与前一个位置关节角之间的差距之间的差值得到明确表示。在选择加权系数的过程中应当按照以下相关原则，即：下臂多运动，上臂少运动。之所以遵循这样的原则，主要是因为基于这样的原则所设计出的内容所具备的优势比较多，因为下臂通常情况下会比上臂更轻一些，这样就能够实现能源的节约，同时也会让整个运动过程变得更加的平稳，使运转的效率得到相应的提升[11]。

2.2 相关遗传算法问题分析

在问题优化的过程中需要设置相应的约束条件，而在本次设计研究过程中在设置了相应的约束条件之后，所得到的经过优化以后的问题可以进行以下表示：

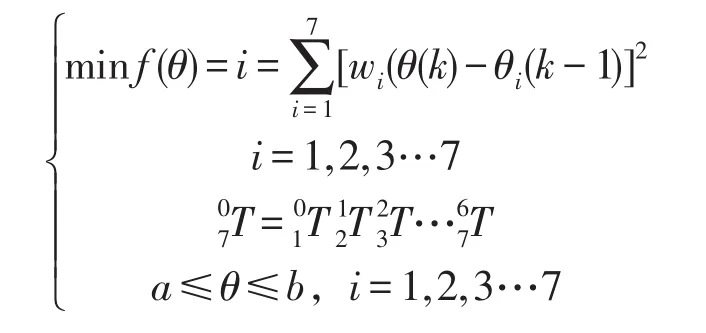
1）编码过程

FGA是直接描述连续关节角的一种算法，而且在具体描述的过程中不需要进行相应的编码和解码过程[12]。与传统的遗传算法相比较而言，FGA的优势明显更多。比如：速度与准确度会更高，可以在大范围之内进行搜索。同时因为不需要解码与编码，所以可以减少这两个环节过程中所发生的困难，与其他相关技术的融合性更高。

2）补偿函数

本次研究所使用的补偿函数，具体表达结果如下所示：

在以上所列出的公式当中，在多数条件下约束条件主要为：a=2，β=2，C=0.5。另外，遗传代数是一个不断增大的过程，因此补偿压力整体上也会呈现出明显的增加趋势[13-14]。最终所得到的函数如下所示：

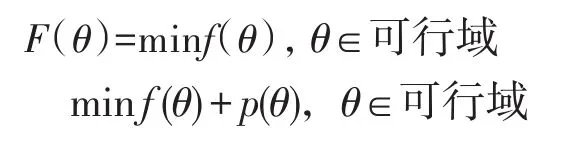
3）具体操作

本次研究过程中竞争性选择算子是实现选择的重要过程。算数交叉算子则是实现交叉的重要环节[15]。本次在方程设置过程中将变异定义为自适应变异，概率值具体设定的数量为0.08，而交叉概率所设置的值则是0.25。

4）仿真图

当所拥有的参数达到了比较完整的预期位姿之后，可以借助遗传算法来进行关节参数的求解，再借助于正运动学方程，这样就可以得到机械臂的具体位姿情况。接着，通过仿真图来观察预期点与机械臂末端可以达到的距离。研究人员也可以通过仿真图来对所得到的运动学正解优良性进行判断[16]。

3 仿真实验及结果分析

神经网络必须要具备好的性能，但是想要确保其性能足够好就必须要接受相应的网络训练。对于冗余机械臂而言，因为逆解的数量是无穷的，因此想要获得可以符合实际需求的逆解还需要进行一定的条件限制，这样才可以将最终得到的逆解作为真正的训练样本。

本次研究过程中在使用遗传算法的过程中同时也结合了比较先进的准则，即最佳柔顺性原则。

本次通过计算得到了相应的训练样本，样本数量共计400组，然后再对RBF神经网络开展专门的训练过程，最终让网络可以达到更加稳定的状态，之后就可以开展仿真与实验的具体验证了。

3.1 仿真实验设计

本次所设计的神经网络为RBF神经网络。该非样本末端位姿点可以使用P1来进行表示。

运动学逆解值的得到还需要借助于遗传算法来开展专门的计算，通过遗传算法的应用，本次所得到的逆解值为：

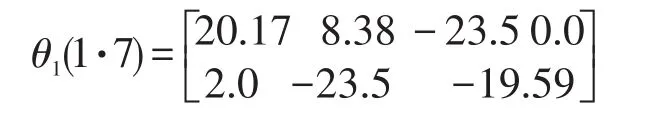
在得到了运动学逆解值之后需要让其与本次研究所设计的RBF神经网络相互结合，这样就可以得到位姿运动逆解值，具体结果如下：

通过对实验所得到的数据比较结果来看，各个数值之间的差异并不是很大，所以误差也都在可控范围之内，而位姿的误差则更小，只有0.1 mm。笔者为了使本次研究所得到的结果及算法有效性得到进一步的验证，专门设计了空间直线轨迹，图2为位姿仿真示意图：

图2 位姿仿真示意图

在研究的过程中选择50个不同的位姿参数，然后再通过本次设计的RBF神经网络得到不同位姿参数的逆解值，再将求得的逆解值直接带入到运动学方程当中。图2当中我们可以发现直线和空间位置点之间的重合程度比较好，这也说明了本次研究设计的神经网络具备一定的效果。

3.2 仿真实验开展

本次所设计的机械臂是在传统6自由度基础上进一步优化升级的7自由度机械臂，为了验证设计出的机械臂实际性能需要开展相应的仿真实验进行验证。

图1当中的机械臂主要构造就是设计成品的简易图。该机械臂的控制系统所采用的控制模式为运动控制卡与IPC控制相结合的方式。

运动控制卡主要是向用户提供和调用DDA指令，DDA制定的工作周期具体为1 ms。如果用户可以将自己已经提前规划好的轴差补点关节角直接输入到缓冲区当中时，控制卡就会自动发出相应的指令。缓冲区的容量足以容纳1 000条指令。7个机械臂旋转关节的轴联动正是借助于这种方式来实现的。

本次所设计的七自由度机械臂主要是在焊接作业当中进行使用。在焊接工作当中，圆弧、直线等都是十分常见的焊接轨迹。所以本次研究所设计的运动轨迹也是圆弧形的。但是圆弧形焊接轨迹在具体的焊接过程中是怎样实现呢？这需要在设计的过程中需要对3个焊接末端位姿点进行示教，首先需要对3个位姿点的数值给出，然后再设计具体的轨迹规划。

本次对规划好的轨迹设计达到的方法主要为：

1）焊枪末端位姿点需要在笛卡尔空间当中给予专门的插补，这样就可以得到中间点位姿。

2）然后再借助于RBF神经网络来得到插补点的逆解值和各轴的关节点数值。

3）通过对DDA指令的调用，然后将插补点所对应的轴关节角数据直接送到DDA缓冲区当中。通过以上流程的完成就可以让圆弧运动轨迹得到实现，最终也可以达到理想的焊接目标。

为了突出本次设计的七自由度机械臂优势，在仿真实验开展的过程中还与传统的六自由度机械臂进行对比。本次设计的基于神经网络的七自由度机械臂精度可以达到93.3%，收敛速度提升15.1%。具体比较结果如表2所示。

表2 七自由度机械臂与六自由度机械臂仿真结果比较

根据表2当中的数据，发现基于神经网络的七自由度机械臂在精度以及收敛速度方面与传统的六自由度机械臂相比均存在显著的优越性，这说明本次所设计与研究的内容也具有较强的实践应用价值。

4 结束语

本次主要是基于神经网络，采用位姿分离的方式来对机械臂的运动学逆解等进行相应的计算与研究。这种方式不仅得到的数值误差小，而且整个计算过程中也十分简单，可以更好的满足机械臂在实际应用过程当中需要进行实时控制的需求。冗余机械臂控制最为关键的环节就是要选择最为合适的关节，而且也需要对冗余关节角度的大小进行明确的确定。本文在传统六自由度机械臂的基础上设计研究七自由度机械臂运动学逆解的内容，整个计算方法简单，优化效果也十分明确，不仅使机械臂的工作效率得到显著提升，而且通过仿真实验也得到了较好的结果。

由于冗余机械臂运动逆解值较多因此需要设置专门的约束条件，在此基础上采取优化策略，达到优化目标，实现对机械臂更加灵活的控制。