基于二自由度转台的双目视觉跟踪技术研究

黄一凡，杨建业，戚国庆

（南京理工大学自动化学院，江苏南京210094）

对室内的运动目标辅助定位，时长期以来人们研究的热点。早在上个世纪70年代末，Jain等人在文献[1]中提出了使用帧间差分的方法来提取运动目标。Birchfield等人[2]提出一种基于颜色及空间的直方图跟踪算法，这种方法不仅利用颜色分布，还利用了像素之间的空间分布关系，提高了跟踪效率。文献[3-5]提出的跟踪算法是基于边缘的直方图特征，这种算法相对于之前的算法可以提取目标更多的信息，获得更加理想的跟踪效果。

目前广泛应用的无人机三维空间定位技术有两种方式：一类是无人机通过携带的装备，如GPS、惯性导航，同步定位与制图（SLAM），获得精确的位置信息，机载设备定位方式是集成在飞行控制系统中，不能独立于无人机，灵活性较差。另一类是借助外设备提供精确的位置信息，如全球卫星定位系统[6]，运动捕捉系统[7-8]，运动捕捉系统拥有高分辨率的摄像头，可以亚毫米级地追踪一个或多个无人机的位姿[9-10]。运动捕捉系统定位精度较高，但其造价较为昂贵，便携性较差，更重要的是，系统需要在目标上安装标记点，更换定位目标时，也需要安装相应的标记点，较为繁琐。因此对于室内目标，设计一种高精度、低成本、便于携带的辅助定位方法，具有重要的需求[11-13]。

针对该问题，本文将目标跟踪与室内定位技术相结合，设计了一套基于二自由度转台的双目视觉跟踪随动系统。通过双摄像头交会定位提高了定位的精度，单片机控制云台转动提高了可跟踪的范围，摆脱了以往单个摄像头在视频跟踪系统中的局限性。

1 摄像机标定

1.1 坐标转换

要将相机坐标系转换成为世界坐标系[14]，需要引入两个矩阵，一个是旋转矩阵R另一个是平移矩阵T。首先假设存在一个点P，它在两个坐标系下的坐标分别标示为那么可以得到以下关系：

上式中，R为正交阵，t为平移向量，是四阶矩阵。

1.2 双摄像机标定原理

图1 双摄像机标定原理图

如图1，假设空间存在一点P，分别从左右相机对P点进行拍摄，再分别用单相机的标定方法对P点进行单独标定，得到左相机的外参和右相机的外参，那么C1（左）相机坐标系的位置用R1和t1表示，C2（右）相机坐标系的位置用R2和t2表示。那么假设任意一点P在C1相机坐标系的坐标是XC1，在C2相机坐标系下的坐标是XC2，在世界坐标系下的坐标是Xw，得到以下关系：

解（2）方程，消去两边共同的Xw，得：

左右相机的外参数如下表示：

最后得到两个摄像机下的坐标关系：

式（6）得到了以左相机为原点的坐标系。

2 目标跟踪

2.1 KCF算法原理

KCF跟踪算法的基本思想是不断对岭回归分类器学习，它的跟踪原理如图2所示。

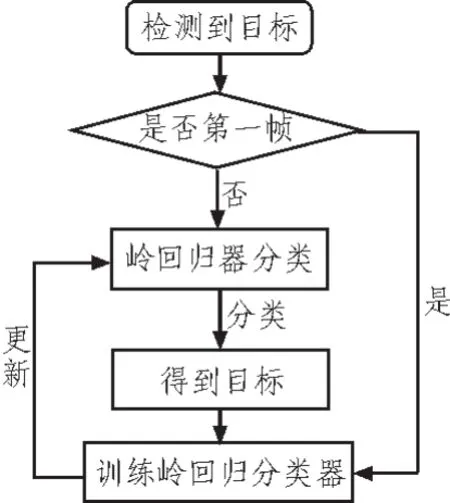
图2 KCF原理图

在训练期间，KCF算法会运用循环矩阵理论对框取的目标区域进行采样，得到正负样本，从而提取出方向梯度直方图特征，将采样得到的所有样本对岭回归分类器进行训练。

2.2 岭回归分类器

首先，对线性岭回归分类器进行训练的目标就是一定要找到一个函数f(x)=wTx，使得损失函数最小，即:

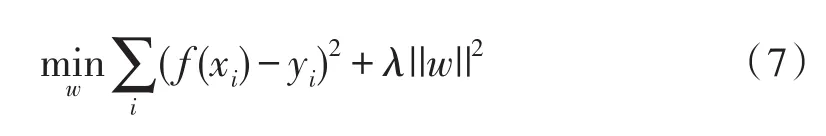
式（7）中x=（x1，x2，…，xn），表示为样本，其中λ为正项，目的是为了防止过拟合，w是所求的参数。通过上面的式（7）可以求出一个封闭解的模式：

式（8）中，矩阵X是基本组合的循环矩阵，y是每个样本的标签值的集合。引入一个核函数理论来对样本进行分类，其思想是把低维空间里面线性不可分的模式通过核函数映射到高维空间实现线性可分，核函数的格式如下：

式（9）中k(x,z)为核函数，φ(x)和φ(z)为映射函数。当使用核函数将样本x映射为φ(x)时，所求的分类器f（x）=wTx中的系数w转化为对偶空间中的a。由表示定理可知，系数ω是样本x的线性组合，即：

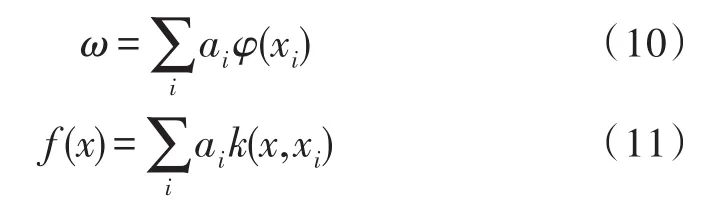
由式（7）和式（11）可以得到：

式（12）中，K为映射之后的核矩阵，Ki，j=k（xi，xj）。在检测阶段，输入的视频经过岭回归分类器的分类来确定最终的目标位置信息，将得到的目标位置信息继续训练岭回归分类器。通过这种反复训练的方法对目标完成跟踪。

3 交会定位

如图3所示，O1、O2表示左右相机坐标系，P表示被跟踪目标，f表示相机焦距，T表示左右相机间距，d是物体分别在两个相机所成的像之间的距离，所以需要求得d的大小，再根据相似三角形的原理求出Z[15]。

即

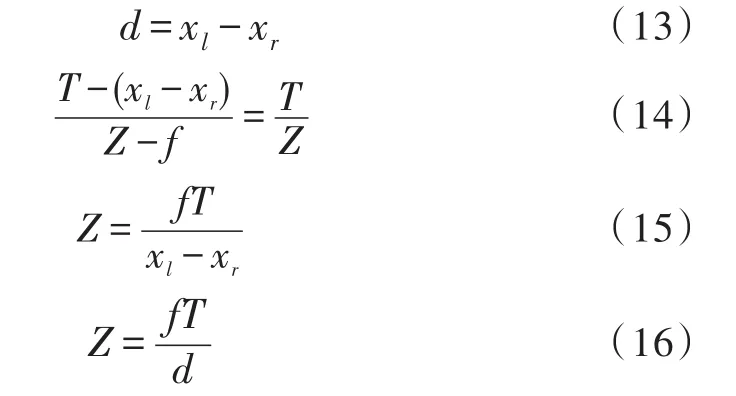
图3 交会定位原理图

4 云台控制

4.1 云台简介

本实验采用的云台是飞宇mini云台，搭载的相机是Gopro4以及Gopro3+。飞宇mini云台是可以通过外部PWM信号进行控制的，PWM波的有效信号范围为：1 020～2 020 μs（1 520 μs是中间值）其中1 000～1 200 μs为锁定模式，1 200～1 800 μs为航向和俯仰跟随模式，1 800 μs以上为航向跟随模式。

信号电平要求3.3 V（如果5 V需加100 Ω的限流电阻），在平衡状态（镜头朝向正前方）时PWM信号脉宽要求 1 520 μs，最大值为 2 020 μs，最小值为1 020 μs。在位置模式下，最大值 2 020 μs对应的位置是电机能转动到的最大位置（镜头朝正下方或正上方）。

4.2 ARDUINO单片机对云台控制

ARDUINO单片机可以生成指定脉宽的PWM波，而在位置模式下，可以控制云台转动指定角度。当生成的PWM波为1020 μs时，对应的角度为0度，当PWM波为2020 μs时，对应的角度为180度。

当跟踪的目标距离相机的上、下、左、右边界200万像素时，通过单片机控制云台，使云台向着相应的方向转动5度，达到对目标的有效跟踪。

5 实验结果展示

图4为实验硬件示意图，双摄像机分别置于二自由度云台上，单片机通过对像素的判断控制云台转动，实现跟踪与定位。

图4 实验设备图

使用Matlab的Stereo Camera Calibrator工具箱对相机标定，得到结果如表1所示。

跟踪和定位程序使用VS2013与OPENCV3.0编写。两个相机处于同一平面且相距15厘米放置，通过上述的标定方法使之处于以左相机为原点的坐标系下。实验设备如图5所示。

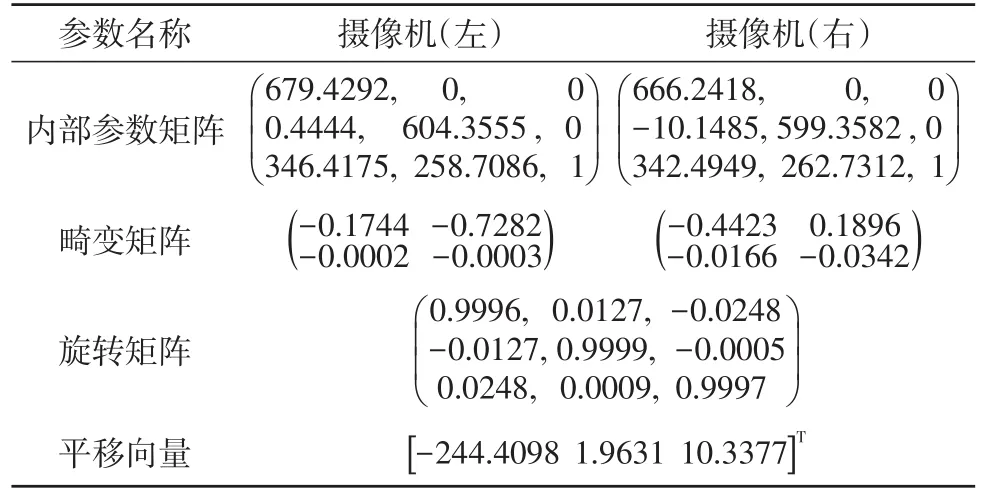
表1 双摄像机标定结果

图5 硬件示意图

选取跟踪的目标后，左右相机的画面分别呈现如图6，当跟踪目标向上运动时，左右相机的画面分别呈现如图7所示。

图6 飞行前跟踪目标

图7 飞行中跟踪目标

可以看出当目标以一定速度向上运动时，KCF算法完全可以跟上框取的运动物体。

将目标的位置数据导出，绘制成目标的位置轨迹图，如图8所示。

通过程序得到其中某一时刻物体的三维坐标分别为x坐标-68.1063 mm，y坐标537.593 mm，z坐标2735.84 mm。

图8 位置轨迹图

由x、y、z3个坐标计算出物体距离坐标原点（即左相机）2.7 m，而用卷尺实际测量出来物体的距离为2.58 m，误差为4.65%。由于相机的标定本身存在不可避免的误差，如果要减小误差，可以增加标定图片的数量或者提高标定板的精度。

6 结束语

本文针对室内定位设计了一套基于二自由度转台的跟踪随动系统。通过KCF算法完成对无人机的跟踪，用交会定位原理得到无人机的位置，通过单片机对二自由度转台进行控制，提高了跟踪范围，实现了双目交会定位，并且通过实验验证了该系统的有效性。