一种低轨卫星通信锥台共形阵列天线设计
2018-08-08赵璐璐余金培
李 凯 ,赵璐璐 ,梁 广 ,吴 迪 ,余金培 1,
(1.中国科学院上海微系统与信息技术研究所,上海200050;2.上海微小卫星工程中心上海201210;3.中国科学院大学北京100049)
现代低轨小卫星具有设备复杂度低(易小型化)、通信时间延迟小、功能与抗毁性强、安全性高、应急能力与灵活性强、实用性与可靠性高、系统建设周期短、投资和发射与运营成本相对较小等特点[1],在科学探测、数据通信和消息传输等领域有着广泛的应用。因此,对具有高增益、轻量化、低仰角等特点的低轨卫星通信终端天线的需求日益迫切[2]。
目前,为了使星载终端天线达到全空域波束覆盖的目的,阵列天线主要采用多面阵列天线、抛物面天线以及共形(曲面)阵列天线3种[3]。文献[4-7]将传统平面阵进行倾斜,使其与水平面形成一定的倾角,这样的阵列利用自有的倾角可以实现主瓣指向更大的俯仰角度,但这种设计会导致旁瓣相对较大。文献[8,9]对天线罩做出了一些改进,利用天线罩的折射效应将全空域覆盖的波束集中到一个小的空域范围内,使得折射后的方向转向低仰角,从而实现低仰角的波束覆盖,但天线罩本身会带来较大的插损。文献[10-12]提出了基于球面共形阵列的发射天线,但由于球面阵列的阴影效应较大,在阵元数较少的情况下,形成波束时会造成增益的损失。
本文提出一种锥台共形阵列天线的设计,分析了锥台侧棱面阵元的坐标与阵列整体坐标的转换关系,并研究了锥台共形阵列天线在全空域内的方向图和增益性能,实现了全空域波束覆盖的目的。
1 锥台共形阵列天线模型
1.1 阵列结构分析
由于所设计的锥台共形阵列可看作由两部分组成,即顶面的平面阵列和侧棱面阵列,而平面阵列阵元与阵列整体坐标系相同,故主要研究侧面棱上各个阵元情况,将锥台共形阵列的几何模型简化成如图1所示的圆锥台形状。
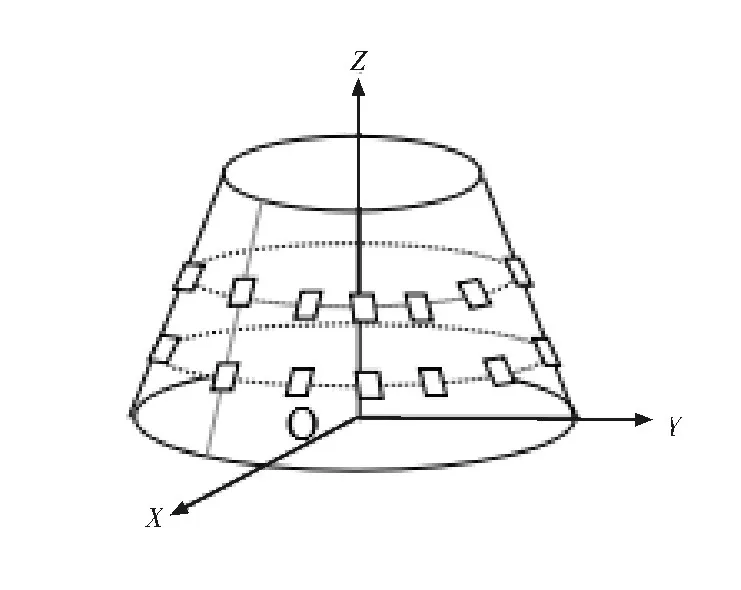
图1 锥台共形阵的几何模型
其中坐标原点位于底面圆的中心位置,设侧棱面上有M个圆环阵列均匀排布,每个圆环共有N个阵元,且阵元沿着锥台的母线等间隔排列,圆环间隔为d,m=1为最底面圆环编号,m延Z轴正方向递增,n=1为第m圆环上与x轴正方向夹角为0°的阵元,沿Z轴负方向看,n延逆时针方向递增。
设第m个圆环上的第n个阵元在整体坐标系下的坐标为(xmn,ymn,zmn),则坐标原点到阵元的距离为:

其俯仰角和方位角分别为

上式中,Δϕ为相邻两阵元方位角的差值。则在极坐标系下,阵元的坐标位置矢量可表示为:

若目标方向的单位矢量为:
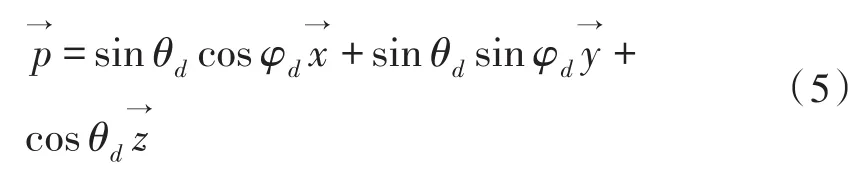
则可得相对于参考点的波程差为:
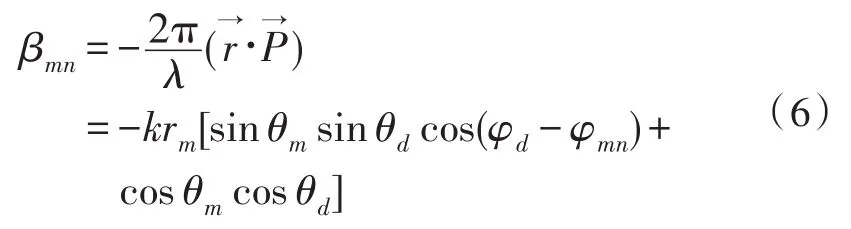
设f(θ,φ)为第(m,n)个阵元在全局坐标系下的方向图,则其导向矢量为:

期望信号的导向矢量为:
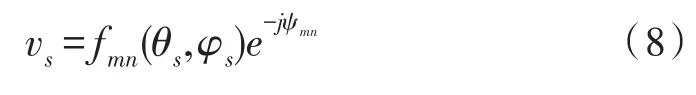
其中,
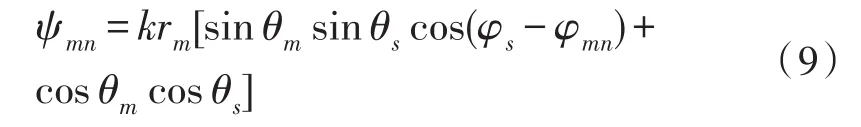
为相对于期望信号的波程差。则阵列天线在远场 (θ,φ)方向上辐射的合成场[13]为:
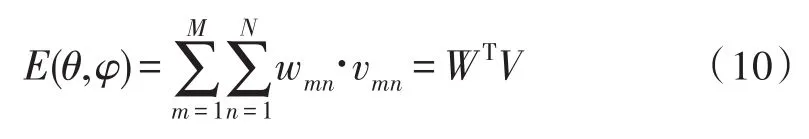
wmn为阵列的复加权矢量。
1.2 空间点坐标在不同坐标系间的转换
坐标转换主要是为了补偿空间不同坐标之间的位置差异,对于平面阵,由于阵列中所有M×N个阵元的方向性系数、增益以及辐射场等是完全一致的,因而阵列天线总的方向图函数表示为:

式中,Δφmn为第(m,n)个阵元与参考阵元间的空间相位差。由此可见,对于平面阵而言,其阵列总的方向图函数可以写成阵元方向图函数与阵因子的乘加形式。
但对于共形阵来说,由于其侧面棱上阵元的局部坐标系与阵列整体坐标系不同,不能直接利用侧棱上的阵元方向图计算阵列的方向图,因此需要将阵元在局部坐标系下的方向图f(θ′,φ′)转换成在全局坐标系下俯仰角为θ及方位角为φ的方向图f(θ,φ),经过坐标转换后的阵元方向图才能进行叠加运算。侧面棱上阵元的全局坐标系O-XYZ和阵列局部坐标系O-X′Y′Z′如图2所示。

图2 锥台全局坐标系与局部坐标系示意图
根据欧拉坐标变换原理[14],空间中任意两个直角坐标系都可以通过对其中一个坐标系进行一系列坐标平移和旋转与另一个坐标系相互重合,这些旋转角被称为欧拉角[15]。对于空间中的任意观察点P,设其在全局坐标系O-XYZ和局部坐标系O-X′Y′Z′中的位置分别为 (x,y,z)和 (x′,y′,z′)。根据坐标变换原理进行转换:将全局坐标系O-XYZ首先绕Z轴逆时针旋转α角度,根据位置关系可得α=φmn,然后再绕Y轴逆时针旋转β角度,β的大小等于锥台的底角大小,若阵元局部坐标系的X′轴与锥台的母线不重合,而是有γ大小的夹角,则需沿Z轴旋转γ角度[16]。整个旋转过程中3次变换矩阵相乘即可得到直角坐标系的变换矩阵:

则点P在两个坐标系下的坐标关系可表示为:
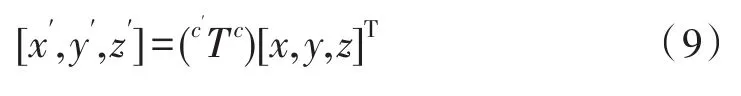
2 锥台共形阵列天线设计
为满足阵列形成波束的俯仰角覆盖到0°~70°的范围,设计了如图3所示的锥台共形阵列天线三维模型。其中锥台顶面共有12个阵元,按照内层4个,外层8个的结构形成两层排布,侧面为12个棱面,每个棱面上放置2个阵元,每个棱面的阵元沿锥台母线均匀排列,且阵元与棱面保持贴合。整个锥台共形阵列共有36个阵元组成,根据不同的波束指向需求,进行相应的波束形成。
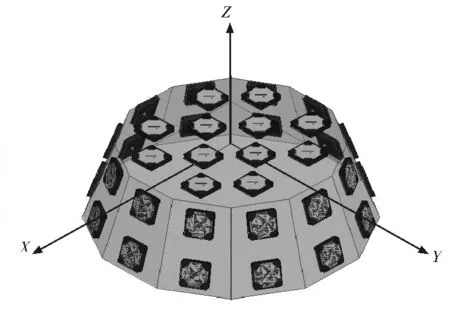
图3 阵列模型图
在实际使用时,可对阵列天线所有的阵元进行编号,使不同的天线单元对每一部分空域负责,阵元编号如图4所示。
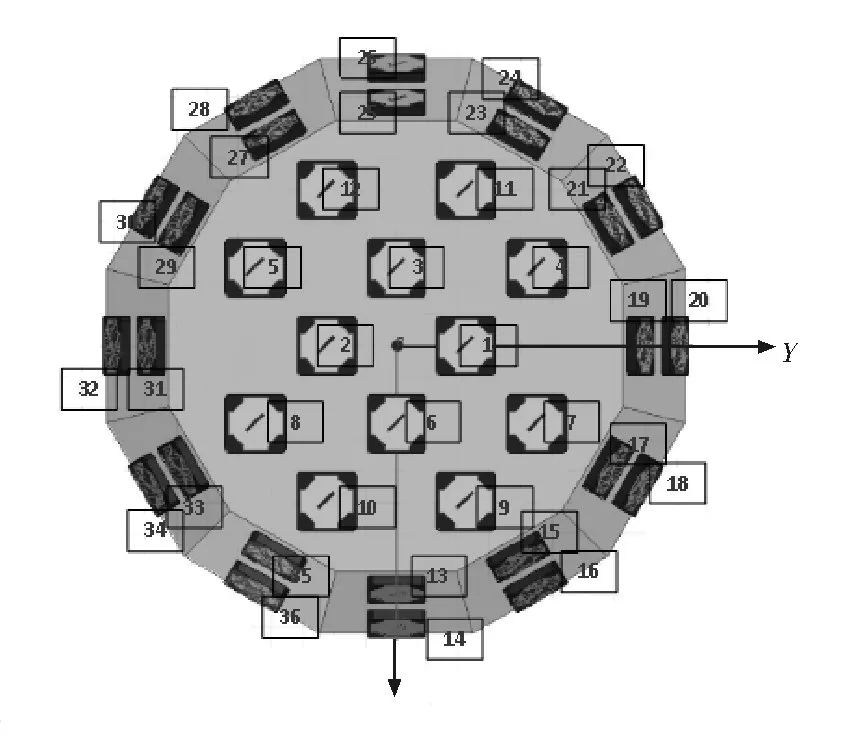
图4 阵元编号
该锥台共形阵列天线顶面和侧面分别负责相应空域内的波束覆盖,可根据不同的需求,将波束指向的加权系数计算后形成查找表,并预存在系统的ROM中,实际使用时直接取出对应的加权系数,选择不同的阵元进行波束形成,从而提高了波束形成的效率。
将整个需要覆盖的空域分为A、B、C 3个不同的区域,同时在B、C大区域中划分多个子区域。其中锥台顶面12个阵元负责覆盖A区域(俯仰角为0~±20°,方位角为 0~360°)和 B区域(俯仰角为±20°~±45°,方位角 0~360°),同时,根据不同方位角选择侧棱面上的阵元对C区域(俯仰角为±45°~±70°,方位角 0~360°)进行覆盖。整个空域共用19个波束即可完全覆盖,波束覆盖情况如图5所示。
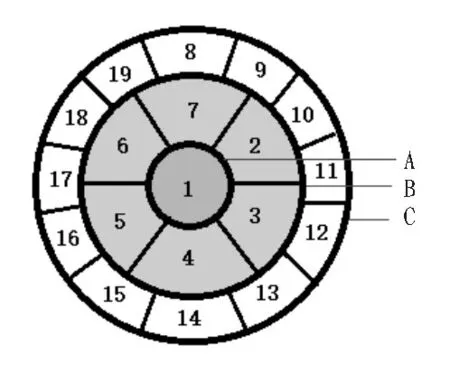
图5 阵列波束覆盖
3 仿真测试及结果
当目标位于某一个子区域空域范围内时,波束指向该子区域的中心位置,若目标进入另一个子区域内,则将波束进行切换。
在所设计的36元锥台共形阵列基础上,分别利用MATLAB和HFSS软件,对指向期望角度的方向图进行仿真测试。下面的仿真图像中,(a)图为俯仰角θ及方位角ϕ联合的三维方向图,(b)图为相应方位角剖面的增益特性。
首先使用顶面的12个阵元分别对A区域的空域进行波束覆盖,假设期望信号方向为锥台的法线方向,即 (θ,ϕ)=(0°,0°),得到方向图如图6所示。
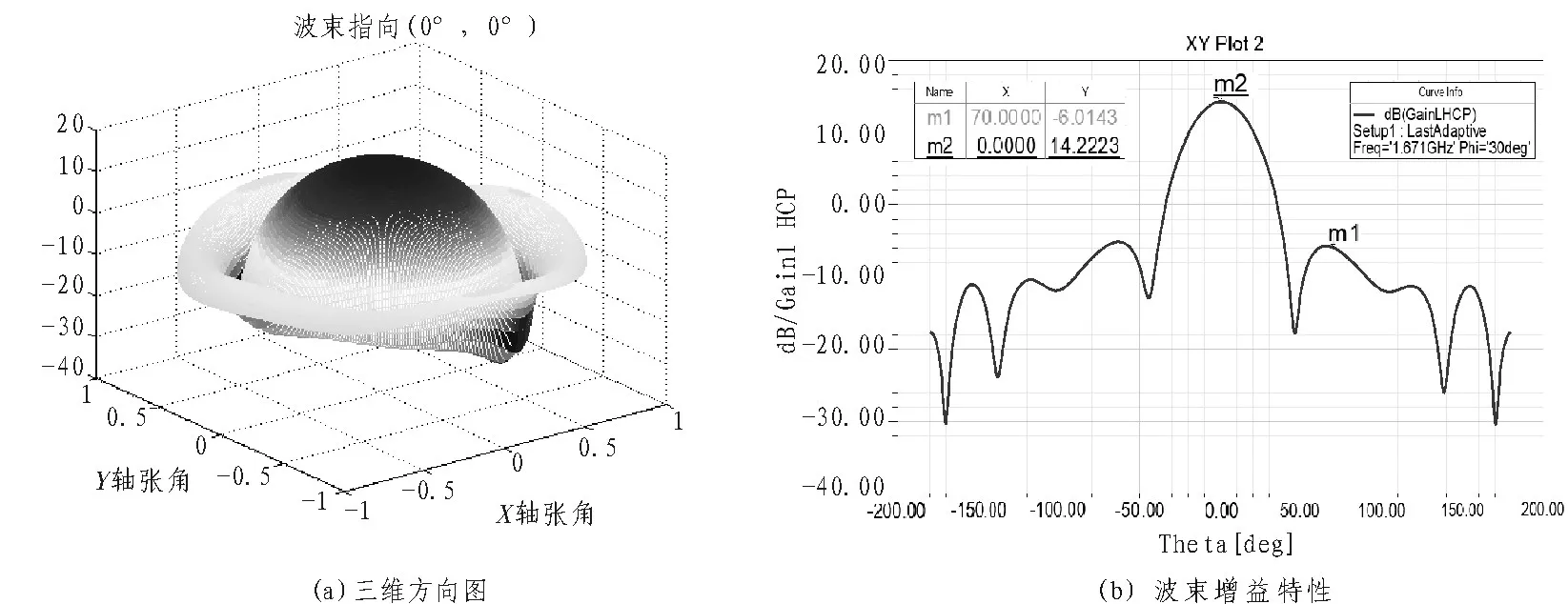
图6 主瓣波束指向(0°,0°)
从图6可以看出顶面阵元形成的波束可以准确指向期望方向,且主瓣最大增益为14.22 dB左右。
为满足对B区域的覆盖,令主瓣波束指向(30°,30°)进行仿真测试,同样使用顶面的12个阵元形成波束,调整阵列权系数使波束指向期望方向,得到仿真验证结果如图7所示。
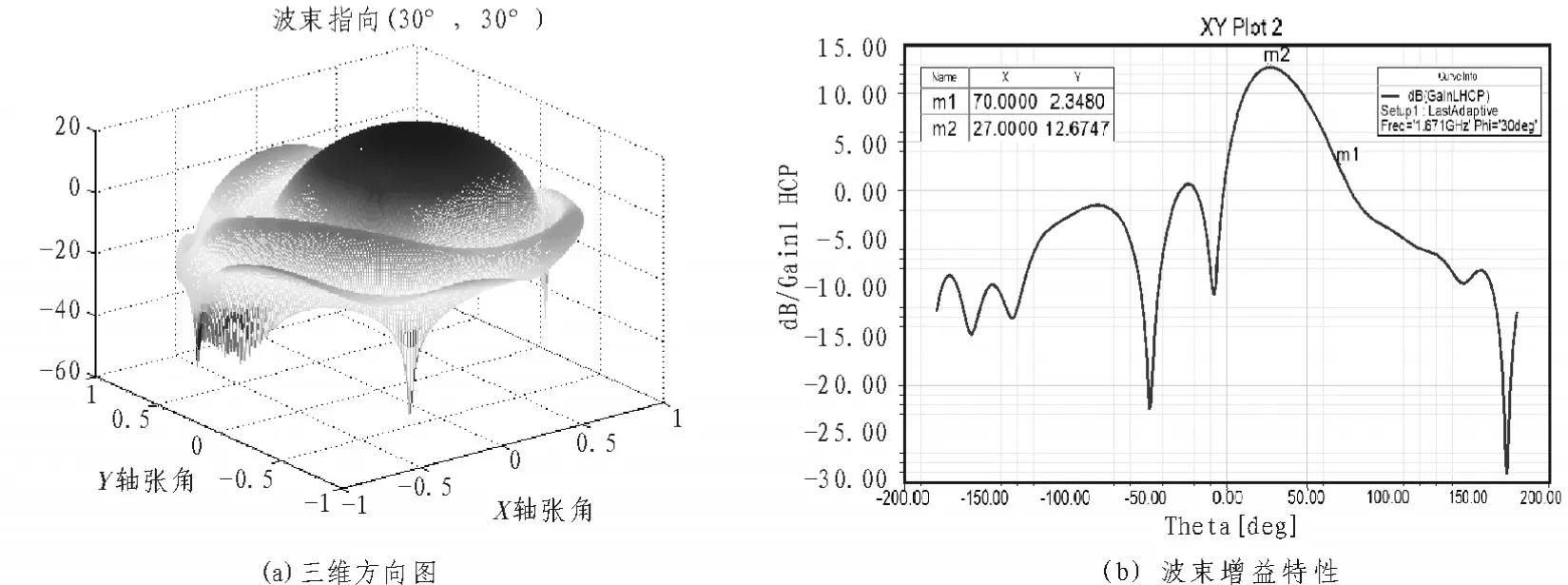
图7 主瓣波束指向(30°,30°)
从图7中可以看出当主瓣波束指向中心为(30°,30°)时,增益最大值约为12.7 dB,且通过权系数的调整可以实现对B区域内的空域覆盖。
图8给出了锥台共形阵列覆盖C区域时三维方向图和增益特性的仿真结果,设定主瓣波束中心在(70°,45°),根据图4中的阵元编号规则,使用侧棱面上的13~20号阵元形成方向图。
由图8可以看出方向图满足波束指向的要求,中心指向能够到达70°,且增益最大值为9.6 dB。
由以上仿真结果可知,阵列主瓣能够准确指向各个期望方向,且主瓣波束增益能够达到设计要求。相比于传统的平面阵列,所设计的锥台共形阵列可以指向更大的俯仰角度,并在大仰角时具有较好的增益特性,能够实现全空域内的波束覆盖。

图8 主瓣波束指向(70°,45°)
4 结束语
本文研究了一种基于锥台形的共形阵列天线,首先建立了锥台共形阵列天线的结构模型,然后分析了锥台共形阵列中局部坐标系到整体坐标系的转换过程,根据坐标变换和方向图叠加原理对共形阵列在不同俯仰角和方位角情况下的方向图进行仿真,结果表明,所设计的锥台共形阵列实现了全空域范围下的波束覆盖,具有较好的应用前景。
