数学教学中对学生解题能力的培养分析

王晓民

（浙江省义乌市第六中学，浙江 义乌）

一、高中数学错题原因剖析

1.概念理解不清

数学概念是人脑对现实对象的数量关系和空间形式的本质特征的一种反映形式，即一种数学的思维形式。正确地理解和形成一个数学概念，必须明确这个数学概念的内涵——对象的“质”的特征，及其外延——对象的“量”的范围。但是，在最初的概念学习的过程中，许多学生就对数学抽象的概念产生了理解困难的现象。由于理解不清，许多学生往往规避此类问题，选择对基本概念不闻不问，仅仅依靠题海战术进行类型题目的解题训练。

2.审题不清

数学语言通常比较简单而精练。因此，在做题目的时候，往往许多学生因为一字之差产生了歧义甚至于偏离了题目原本的思路。因此，审题不清就成了大多数学生的口头禅。值得注意的是，审题不清的现象多出现在采用题海战术的学生身上。由于做题量巨大，进而在考试中看到类似问题时，没有对出题人的意图进行揣摩而直接套用之前的解题模板。

3.强调题海战术

数学问题往往一题多解，因此喜欢题海战术的学生通过大量的练习积累了大量的解题方法。但是，在具体的解题过程中，只知道生搬硬套，把抽象的数学学习变成了文科的死记硬背。数学的复习当然离不开题目的练习，但是这并不意味着就需要题海战术。不会解题，方法不当，无法理解问题的含义往往与学生自己的做题数量有较大关系。无法及时抓住解题的关键点，既浪费了解题时间，同时降低了正确率。

二、高中数学错题应对策略

1.重视概念的理解

概念的理解必须放在第一位。作为数学学科的基本框架，概念的学习与理解对理解相关知识整体有着非常重要的作用。在学习中，我们要静心对相关数学概念进行理解。理清概念阐述的内涵，在此基础上，结合少量的习题，可以帮助我们有效提高解题速度，降低细节错误发生率。

案例1：指数概念的引入

引例1：细胞分裂时，第一次由1个分裂成2个，第2次由2个分裂成4个，第3次由4个分裂成8个，如此下去，如果第x次分裂得到y个细胞，那么细胞个数y与次数x的关系式是什么？y=2x

引例 2：《庄子·天下篇》：“一尺之棰，日取其半，万世不竭.”

设木棍原长为1，第x次剩下的木棍长y与x的关系式是什么？

这两个表达式都是函数，共同特征是自变量出现在指数位置上，如果将它们自变量的范围推广到实数R，就是我们今天要学习的一类新函数——指数函数。

定义辨析

在下列的关系式中，哪些是指数函数，为什么？（学生讨论）

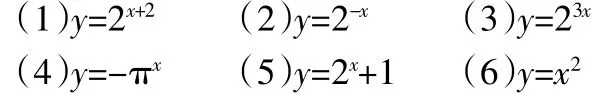
在上面指数概念的学习中，我们发现通过生活的实例以及对比可以帮助同学们很好地掌握指数函数的概念。

2.总结解题技巧，灵活运用

数学的解题能力的确需要我们进行大量的做题训练。但解题能力不代表做得多，不代表就是题海战术。我们需要在做题的时候，及时对自己的错题和经典题型进行总结，从而在提高阅读能力的基础上，完善自己的解题技巧。我们知道高考数学只有两个小时，考场上寸秒寸金，解题能力的提高必将成为我们高考中取得较好成绩的一个重要手段。总结在解题过程中的问题所在，理解出题人的出题意图，使高考中的“陷阱”在我们面前显露无疑。

案例2：

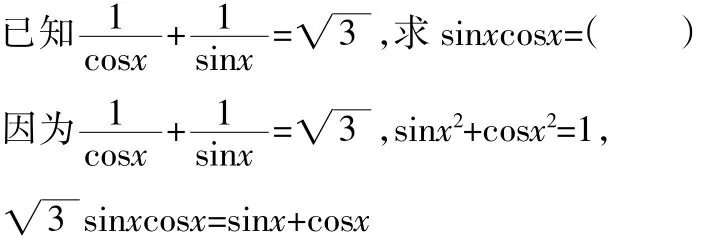
两边平方展开，我们发现可以将sinxcosx看成t，然后可得到3t2-2t-1=0

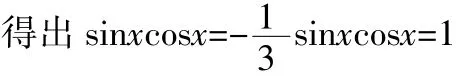
这个题目在解题的时候很多同学往往会得到两个解，实际上此题在两边平方的时候就已经出了问题。但是不用平方做似乎又没有办法解，那么问题就在如何检查了。我们需要从问题这个角度去解决这个问题。我们知道利用二倍角公式可得sinxcosx=，所以此题的范围必然为所以断不能取1。

这个案例也告诉我们检查答案可以从问题入手，通过问题的范围来解决多解问题。高中数学在高考中占有非常重要的位置。因此，提高数学的解题能力对于提高高考成绩有着重要的实际意义。因此，要使学生的解题能力达到较高水平，并上升为一种创造才能，就要在整个教学的过程中，始终都要注意培养和发展学生解题能力的各种因素，注意提高学生的整体素质。只有这样，解题能力的提高才有根底和源泉，解题的功底才扎实。