激光切割视觉系统单目摄像机快速标定方法
2018-08-08杨煜俊陈洵凛许征波
杨煜俊,陈洵凛,许征波
(广东工业大学机电工程学院,广东 广州 510006)
1 引 言
相机标定是计算机视觉领域中的一项重要研究课题,是实现 3D 重建、视觉测量的基础。在对视觉系统的精度有较高要求的场合,往往要借助几何尺寸已知的靶标完成相机的标定过程[1-4]。同时摄像机标定是计算机视觉领域里从二维图像获取三维信息的基本要求[5-6],是完成许多视觉工作必不可少的步骤。其目的是确定摄像机内部的几何和光学特性(内部参数)以及摄像机在三维世界中的坐标关系(外部系数)[7]。随着机器视觉的不断发展与摄像机的普及,用一种简易、灵活的标定方法去完成与视觉有关的工作对许多非视觉专业人士来说是非常需要的。
针对这一情况,文献[8]提出了一种新的基于最小凸包理论的棋盘格特征点自动提取算法,利用张正友标定模型进行参数的自动计算,并以文本形式输出。该方法的优点是操作简单高效,但标定精度没有得到改善。文献[9]提出了基于Poncelet定理的相机参数简易标定法,该方法的优点是精度较高,优于目前典型的简易标定法。但方法在求取相机外参时只适用于双目视觉系统。文献[10]提出了基于张正友标定法的一种改进的两步标定法,该方法把作为解析解求解出来的初始参数用非线性最小二乘法进一步完善,得到了内外参数。因此该方法提高初始数值的鲁棒性,但有标定过程复杂、计算繁琐等问题。
综合上述的情况,本文提出一种九圆点的单目摄像机快速标定法,即先求出图像九点和定义在世界坐标系X-Y平面上的九点模板之间的单应性矩阵且线性求解出摄像机内参与畸变系数,通过摄像机内参数矩阵和像机畸变系数矩阵校正映射求解出图像的X、Y坐标重映射参数。然后使用双线性插值法重映射来校正有畸变的图像。最后在矫正后的图像中求出内外共八个仿射投影矩阵,并取其均值作为最终投影矩阵来求解出世界坐标。
2 摄像机模型
2.1 线性模型分析
本文中选取的摄像机模型中常用的针孔模型,分别建立图像平面坐标系(O1xy),摄像机坐标系(OcXcYc)以及三维世界坐标系(OwXwYw)如图1所示。
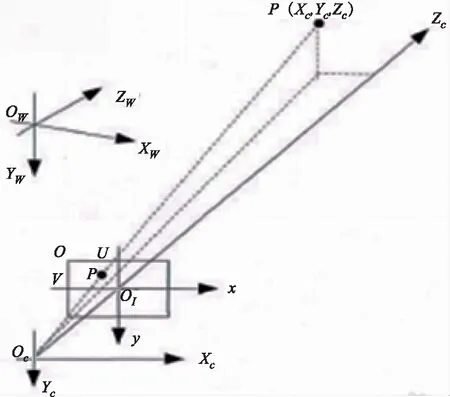
图1 针孔摄像机模型
在图像上定义直角坐标系(Ouv),(u、v)表示以像素为单位的图像坐标系的坐标,(x、y)表示以mm为单位的图像坐标系的坐标,在X、Y坐标系中,原点O1定义在摄像机光轴与图像平面的交点,该点一般位于图像中心,但是由于制造原因,很多情况下会有偏移,若O1在u、v坐标系中坐标为(u0,v0),每一个像素在X轴与Y轴方向上的物理尺寸为dx、dy,则图像任意一个像素在两个坐标系下的坐标有如下关系:
(1)
摄像机坐标系与世界坐标系之间的关系可以用旋转矩阵R与平移向量t来描述:
(2)
则由式(1)和式(2)可以得到像素坐标与世界坐标的转换关系如下:
(3)
其中,fx=f/dx,fy=f/dy;f为相机的焦距;R为旋转矩阵;t为平移量;M1为像机内参数矩阵,M1M2即为图像坐标系与世界坐标系之间的单应性矩阵。
2.2 畸变模型分析
径向畸变是由光学系统缺陷造成的成像的径向畸变,特点是成像以主点为中心向径向方向发生变化。分为枕型失真和桶型失真。径向畸变的数学表示模型为[11]:
(4)
其中,xu,yu是针孔模型下的理想坐标;x,y是实际情况下的图像物理坐标;k1与k2是径向畸变参数。
偏心畸变是指光心在成像平面的偏移,是由于相机的工艺水平,光轴与成像平面不能完全垂直造成的。偏心畸变的数学表达式模型为[11]:
(5)
其中,xu,yu是针孔模型下的理想坐标;x,y是实际情况下的图像物理坐标;p1与p2是偏心畸变参数。
3 新算法
3.1 基本思路
首先在世界坐标系OWXWYW平面上打出3×3阵列形九点,如图2所示。记录每点在世界坐标系下的坐标。基于开放计算机视觉函数库(Open CV)中的findCirclesGrid函数提取出图像中九个角点的图像坐标。该位置与角点的真实位置最大有几个像素的误差,为了获得高精度的相机标定结果,需要提取亚像素精度的角点位置[12-14]。以最大迭代次数和设定精度的组合来亚像素精确化角点图像坐标。本文算法设置最大迭代次数为30,设定精度为0.1。然后以九点的世界坐标系坐标和图像坐标系坐标求解出其单应性矩阵且线性求解出摄像机内参与畸变系数。通过摄像机内参数矩阵和像机畸变系数矩阵校正映射求解出图像的X、Y坐标重映射参数。再使用双线性插值法重映射来校正有畸变的图像。最后在矫正后的图像中求出内外共八个仿射投影矩阵(外四个仿射投影矩阵分别是ΔACG,ΔCAI,ΔICG,ΔGAI四个三角形各自的三个顶点的图像坐标与世界坐标之间的仿射投影矩阵,内四个仿射投影矩阵分别是ΔEBD,ΔEBF,ΔEFH,ΔEDH四个三角形各自的三个顶点的图像坐标与世界坐标之间的仿射投影矩阵),并取其八个矩阵的均值作为最终投影矩阵(单应性矩阵)来把图像中的目标坐标转成世界坐标系下的坐标。
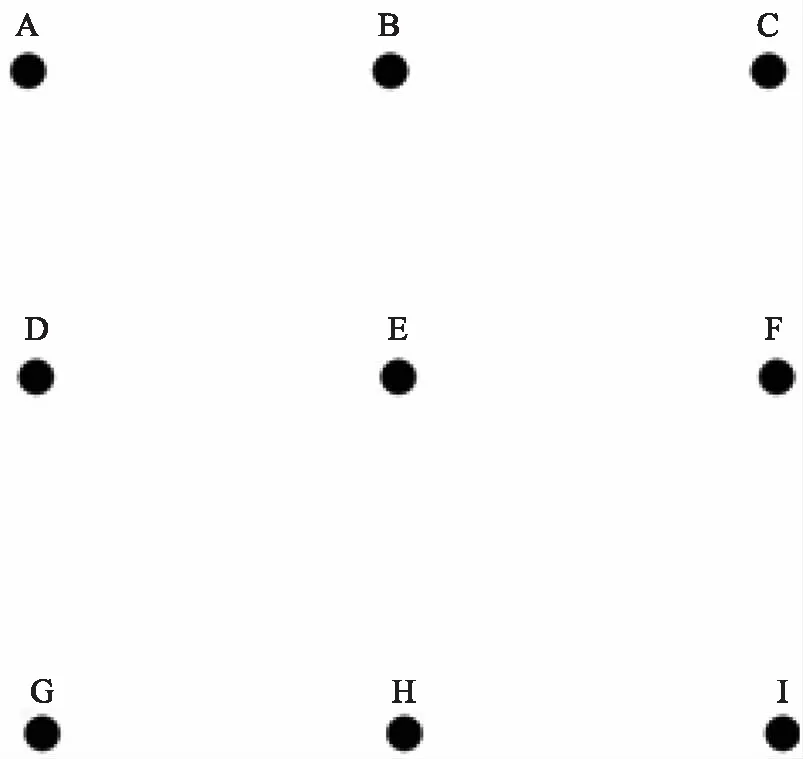
图2 3×3阵列形九点
3.2 算法流程图
图3为算法的流程图。
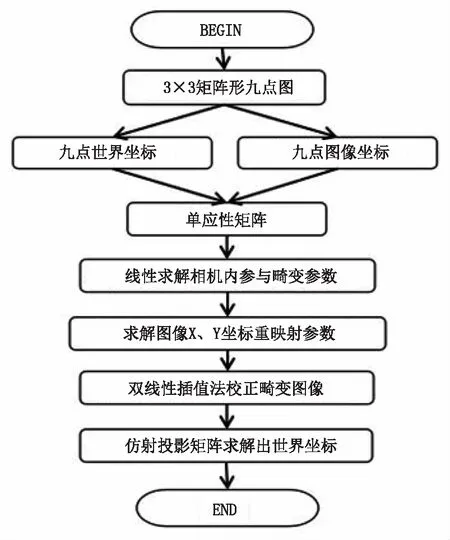
图3 算法的流程图
3.3 算法的优点
相对于张正友的一般圆点标定算法,九圆点的单目摄像机快速标定方法具有以下的优点:
①用少数的特征点来求解单应性矩阵,其结果更加稳定。
②求解相机内参与畸变参数均基于亚像素精确化模型进行优化,确保了结果的高精度。
③像差模型不仅考虑了径向畸变,而且考虑了偏心畸变。
④求解内外八个仿射投影矩阵的均值,而非透视投影矩阵来求解世界坐标,既保证了速度,又保证了精度。
4 算法的实验验证
为了检验算法的性能,本文以激光切割机和佳能单反数码相机搭建实验平台进行真实图像实验。如图4所示,下面为激光切割机,在激光切割机的正上方装的是单反数码相机,相机的型号是佳能1300 d 。
实验在同等条件下进行,以九圆点快速标定法和张正友的一般圆点标定法分别进行实验并对其结果做比较。图5为实际用来标定相机的圆点图以及亚像素精确化提取出点的结果。

图4 激光切割机和佳能单反数码相机实验平台

图5 实际用来标定相机的圆点图
相机在九圆点标定法和一般圆点标定法这两种方法标定完成后分别保存输出其各自图像像素坐标转成世界坐标的转换矩阵。在激光切割机上随机打出5个点并分别记录其每点的机床坐标,经过图像处理精确找出图像中5个点的像素坐标,并与以上两种标定方法输出的转换矩阵相乘转成世界坐标(机床坐标)。记录以上的数据和实验结果如表1所示。
从表1中可以看出:在同等条件下九圆点快速标定法的标定精度相对于张正友一般圆点标定法的标定精度高,偏离误差小,标定速度也提高了很多。因此,九圆点快速标定法在标定过程中既保证了标定速度,又保证了标定精度。
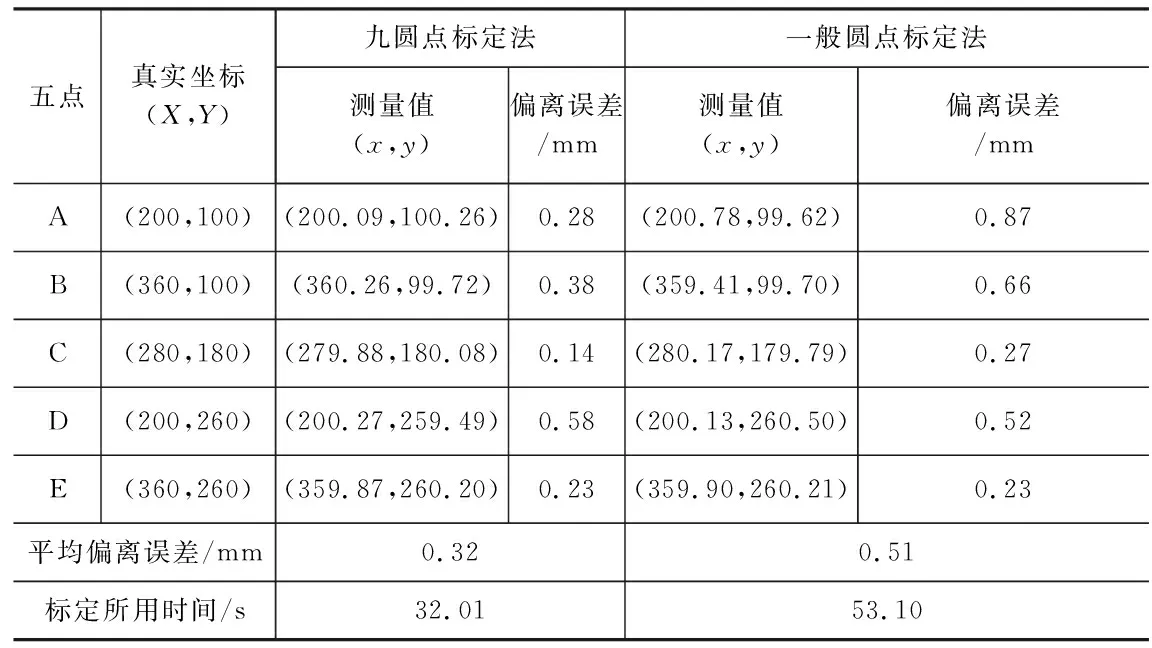
表1 九圆点标定和一般圆点标定的实验结果
5 结 论
对目前激光切割机结合视觉切割行业来说,现有标定算法中存在计算量大,导致标定时间过长,求解透视投影模型的特征点多,从而算出的透视投影矩阵精度不是很高,结果不稳定。而本文中采用的九圆点快速标定法可以有效地克服这些问题。由于特征点少,简化了标定过程的计算量,从而使标定时间更快,结果更稳定。又是基于特征点的亚像素精确化求解仿射投影矩阵(而非求解透视投影矩阵)和内外八个仿射投影矩阵的均值作为转换矩阵,从而使标定的精度更高。实验结果证明,本文所述的标定算法的性能优于张正友一般圆点标定算法。
