二元结构平原地区水库浸没预测方法研究

王 碧，杜兴武，胡 成，罗 垚

(1.中国地质大学(武汉)环境学院，湖北 武汉 430074;2.湖南省水利水电勘测设计研究总院，湖南 长沙 410001)

水库浸没是指水库蓄水后，库区周围地下水受库水顶托作用，排泄受阻，导致地下水水位壅高，使其可能接近或者高于地表而导致该地区土壤次生盐碱化、沼泽化以及建筑物地基条件恶化等危害[1]。一般来说，在平原地区修建水库，正常蓄水位一般限制在一级阶地附近，也有不少水库利用两岸堤防抬高水头。由于平原地区库岸地形平坦开阔，地面高程与正常蓄水位相差不大，地下水埋深较浅，易形成浸没问题，且浸没面积一般较大，因此对平原地区水库浸没范围进行预测很有必要[2]。浸没问题是平原地区水库勘察设计和建设中最重要的水文地质问题，对于常见的冲积成因二元沉积结构的平原地区，我国现行的《水利水电工程地质勘察规范》(GB 50287—99)[3](以下简称《规范》)中采用的卡明斯基法在实际工程应用中存在诸多问题。为此，本文分析了利用卡明斯基法对二元结构平原地区水库浸没进行预测所存在的不足，并从黏性土的渗透性规律入手，在“启动水力梯度”的基础上，提出了适用于承压含水层模型的折减系数法的计算公式，最后通过实例应用，对比分析了卡明斯基法、折减系数法和数值法3种预测方法对二元结构平原地区水库浸没范围预测结果的适用性和准确性，以为类似工程水库浸没问题研究提供参考依据。

1 水库浸没的预测方法

1.1 卡明斯基法

对于双层结构地层，《规范》中采用卡明斯基法进行水库浸没范围预测。

其计算公式如下：

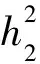
(1)

根据上式计算得出的地下水水头壅高值H，结合水动力学法可推导出地下水壅高水头线方程[4]为

(2)

上式中：M为下部含水层(砂砾石)的厚度(m)；K1为下部含水层(砂砾石)的渗透系数(m/d)；K2为上部含水层(黏性土)的渗透系数(m/d)；h1、H为起始断面蓄水前、后地下水水位至含水层顶板的厚度(m)；h2、y为计算断面壅水前、后地下水水位至含水层顶板的厚度(m)；Yx为壅水后任意断面的地下水水位值(m)。

卡明斯基法以上层黏性土底板为计算基准面，水库浸没区计算示意图见图1。

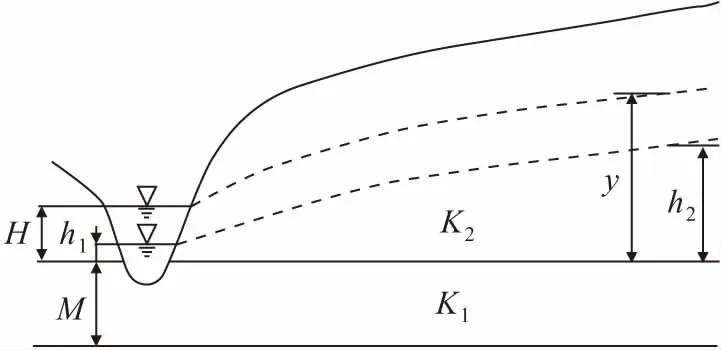
图1 水库浸没区计算示意图Fig.1 Calculation diagram of the reservoir immersion zone

利用该方法对二元结构平原地区水库浸没进行预测存在以下不足：①卡明斯基法计算模式是地下水补给库水，水库蓄水后导致地下水水位整体抬高，但地下水水位仍大于水库水位，整体的补给关系不变。而平原地区地形平坦、地面高程较小，平原地区修建的水库水位一般在河流一级阶地附近，甚至利用两岸的堤坝抬高水头，导致库水位高于两岸一级阶地。水库蓄水后库水位往往高于地下水水位，补给关系发生了改变，由库水补给地下水，导致地下水水位壅高；②分析卡明斯基法计算公式得出的地下水壅高水头线(见图1)可知，离水库越远地下水水位越高，其浸没程度越大，在堤脚处浸没程度最小。而工程实际情况是，在地形相差不大的情况下堤脚处浸没程度最大，远离水库其浸没程度逐渐减小；③平原地区二元结构地层中上层为渗透系数较小的黏土层，其厚度较大，而下层为渗透系数较大的砂砾层，两者级差大于102，黏土层可视为弱透水层或相对隔水层，其阻水作用不能忽略，采用承压含水层模型计算会更加符合实际。而基于潜水含水层模型的卡明斯基法计算公式显然已不适用于这种情况，其忽略了上层黏性土的阻水性[5]。

以上三点原因是造成该规范提供的方法不适用于平原地区二元结构地层的主要原因，将会导致预测结果出现偏移，由于上层黏性土的特殊性，应当采取新的方法来预测水库蓄水后的地下水水位壅高值，使得计算结果更加接近实际值。

1.2 折减系数法

1.2.1 考虑起始水力梯度(I0)

张忠胤[6]研究指出黏土中存在大量的结合水，其对水的流动起到阻碍作用，并提出了“起始水力梯度“的概念，即黏性土中当水力梯度很小时，不存在显著的渗流，只有当水力梯度达到一定值后才会出现流动的水，这个值就是“起始水力梯度”(I0)。水在黏性土中的渗流运移具有较复杂的形态，其渗透性规律可用下式表示：

v=K(I-I0)

(3)

式中：v为渗透流速；K为黏性土的渗透系数；I为水力比降，即水力梯度；I0为起始水力梯度，即为v-I直线段延长在I轴线的截距，见图2。

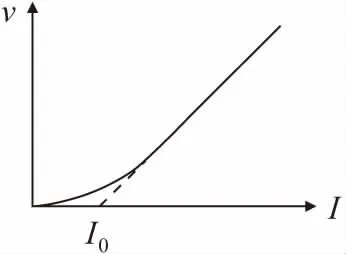
图2 水在黏性土中的渗透规律曲线Fig.2 Curve of the water permeability in the cohesive soil

由公式(3)可知，当水力梯度I小于I0时，水在黏土中不产生显著渗流现象；而当水力梯度I大于I0时，v-I曲线呈线性关系，因此I0是表征黏性土渗流特性的重要指标之一。

由于起始水力梯度的存在，承压含水层中的地下水在顶托作用下逐渐向上覆的弱透水层渗透,在竖直方向上，弱透水层中的水头损失与穿透厚度成正比例关系，该渗透规律已在部分工程实践中得到了验证[7]。如图3所示，当钻孔达到a点时，刚好能观测到稳定的地下水水位，随着钻孔加深至b、c点，地下水水位分别上升了ΔH1和ΔH2，当钻孔揭穿黏土层到达下部含水层时，地下水水位上升至距黏土层底板以上处H0，显然：

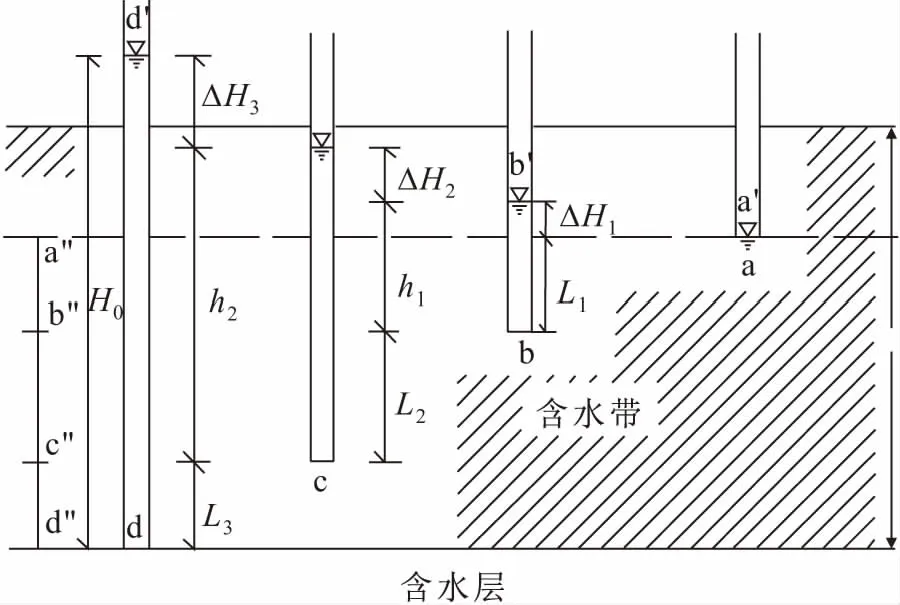
图3 弱透水层中的含水带示意图Fig.3 Diagram of the water-bearing zone in the aquitard

ΔH1/L1=ΔH2/L2=ΔH3/L3

=(ΔH1+ΔH2+ΔH3)/(L1+L2+L3)

=(H0-T)/T=I

(4)

由于各点地下水水位是稳定、静止的，故v=0，由此得出I=I0。故可推导出任意断面的黏土层中含水带厚度T的表达式为

T=H0/(I0+1)

(5)

式中：H0为下层含水层的测压水位高度；I0为黏土中的起始水力梯度；T为弱透水层中的含水带厚度，其上界面即为水库蓄水后地下水水位壅高位置。

1.2.2 承压含水层模型

平原地区的二元结构地层中由于上层黏性土渗透系数很小且厚度较大，黏性土可视为弱透水层，下层可视为承压含水层。因此，采用承压含水层模型计算地下水水位壅高值更加符合实际情况[8]。

由于下层承压的水头不是一个定值，随着距堤坝距离的增加，承压的水头呈线性降低，见图4。由公式(5)可知，黏土层中的含水带厚度与下层承压水头成正比例关系，因此该含水带厚度也是一个变化值。为了计算出黏土层中含水带厚度，只需求出下层承压水头的变化规律即可。

图4 二元结构承压含水层模型示意图Fig.4 Diagram of the confined aquifer model with dual-formation structure

水库蓄水前，在堤脚处通过钻孔钻穿上层黏土层，获得砂砾层的承压水头H1；然后在计算剖面的最远端距堤坝Lm处，同样通过钻孔获得H2；利用水动力学中承压水一维稳定运动模型，可得出单宽流量的计算公式为

(6)

(7)

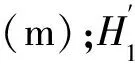
以上层黏性土底板为计算基准面。将公式(7)代入公式(5)中，可得到黏土层中含水带厚度的计算公式为

(8)

通过上式即可计算出平原地区二元结构地层中水库蓄水后上层黏性土中地下水水位的壅高值，从而得出水库浸没范围。该黏土层中含水带厚度T是个变化值，随着距堤坝距离x的增加，T减小，相应的水库浸没程度降低，符合实际情况。

1.3 数值法

在预测二元结构平原地区水库浸没范围时，因研究区域内地下水水文地质条件较复杂，地下水往往呈空间三维运动状态，渗流场的时空分布难以用解析方法计算。为了预测在库水位抬升的影响下库周地下水水位雍高及其所造成的水库浸没范围，需要在分析研究区水文地质条件的基础上，建立水文地质概念模型，并采用数值法求解。

利用数值法求解主要有以下4个步骤：一是通过对研究区的水文地质条件进行合理概化后，建立符合研究区实际情况的水文地质概念模型；二是将该水文地质概念模型进行转换，建立与之对应的地下水渗流数学模型；三是将该数学模型在数值模拟软件中转为可视化的地下水渗流数值模型。经过上述转换过程建立的地下水渗流数值模型是否能全面、客观地表征研究区实际的水文地质条件和特征，还需要对该模型进行识别与验证，也称之为“反演”，即数学运算中的解逆问题，就是利用水头函数求解地下水均衡方程。由于水头函数受地下水均衡场内多个水文地质条件控制，因而它是一个多元函数，模型验证时需对研究区内各种水文地质参数进行调整，具体做法是根据观测孔的资料，反求水文地质参数；四是将“反演”算出的最优参数值代入地下水渗流数值模型中，计算得到预测结果。

2 实例应用与分析

2.1 研究区概况

湘江长沙综合枢纽工程位于湘江干流下游的长沙市望城县境内，坝址选定在望城县境内的湘江蔡家洲，位于长沙市城区下游约20 km。坝址至上游长沙市区浏阳河库段均属于垸内型的库区，堤坝内的平原区地势低缓，地形平坦开阔，是水库浸没易发地带，见图5。

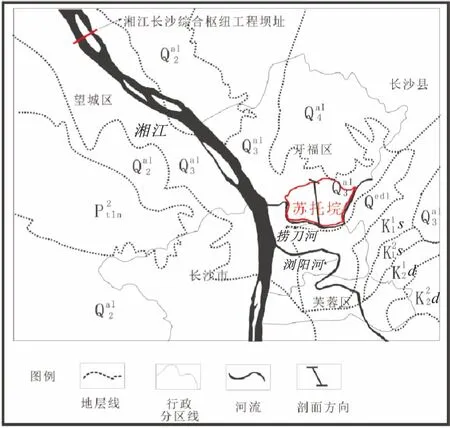
图5 苏托垸地区平面简图Fig.5 Plane diagram of the Sutuoyuan area

本文选择水库东岸苏托垸地区为研究区，区内为典型的平原地区二元结构地层，上层为黏土层，下层为砂砾层，主要为第四系地层，其特点如下：

(4) 残坡积地层(Qedl)：岩性为黄褐色、红褐色黏土、黏土夹碎石，可硬塑状，主要分布在低山、丘陵等坡麓地带。

由钻孔资料得出黏土层底板高程为25 m，天然情况下，研究区段捞刀河天然水位为25.45 m，达到正常蓄水位29.7 m高度时，按照捞刀河河面的水力坡降值得出河水位为29.76 m。当捞刀河河水位为27.5 m时，堤坝处承压水位为27.6 m，与河水位基本一致，在远离堤坝L=2 000 m处的观测孔内承压水位为27 m。由于承压含水层与河水之间水力联系非常紧密，且相距很近，故两者水位近似相等。据现场压水试验结果，上层弱透水层的渗透系数K2为2.0×10-5cm/s，厚度为5 m，下层强透水层的渗透系数K1为1.5×10-3cm/s，厚度为7 m。

在研究区水库浸没评价时，本文根据苏托垸地区的地形特点，并结合观测孔布置情况，在远离堤坝L=2 000 m处选取具有代表性的剖面(见图5)，利用卡明斯基法、折减系数法和数值法3种方法对水库浸没范围进行了预测。

2.2 卡明斯基法预测

本文利用卡明斯基法计算公式(1)，可计算得出距离河流L=2 000 m处的地下水壅高水头值H，通过计算得出Lm处的地下水水位值为31.29 m。

将该参数代入公式(2)，化简得到水库蓄水后地下水壅高水头线方程为

(9)

将利用卡明斯基法计算得出的地下水水位线绘制在研究区地形剖面上，并结合前述的水库浸没评价标准，绘制临界地下水水位线，见图6。

由图6可见，利用卡明斯基法计算公式预测得到的水库蓄水后苏托垸地区地下水水位线接近地表，甚至在平坦及低洼地段溢出地表，而临界地下水水位几乎都高于地表，也就是说，水库蓄水后整个苏托垸地区均为浸没区。

图6 利用卡明斯基法预测得到的苏托垸地区地下水水位剖面图Fig.6 Cross section of groundwater level using Kamenski method in Sutuoyuan area

2.3 考虑起始水力梯度后的折减系数法预测

本文通过现场钻孔试验及长观孔数据，得出起始水力梯度I0=0.36，将所有参数代入折减系数法计算公式(8)，可计算得到任意断面的黏土层中含水带厚度，从而推导出水库蓄水后上层黏土层中地下水壅高水位线方程：

(10)

因此水库蓄水后地下水壅高水头

Yx=T+25=28.5-2.2×10-4x

(11)

将利用折减系数法计算得出的地下水水位线绘制在研究区地形剖面上，并结合前述的水库浸没评价标准，绘制临界地下水水位线，见图7。

图7 利用折减系数法预测得到的苏托垸地区地下水水位剖面图Fig.7 Cross section of groundwater level using the reduction factor method in Sutuoyuan area

由图7可见，距离捞刀河越近，地下水水位壅高值越大，远离堤坝，地下水水位降低，符合实际情况。此外，距离堤坝越近，水库浸没程度也越大，符合常理。

2.4 数值法预测

本文采用有限元数值模拟软件FEFLOW对苏托垸地区水库浸没区进行数值模拟预测。根据苏托垸研究区实际条件，可将该地区地下水流概化为非均质各向同性3D水流模型，边界条件设置如下：东南西三个方向均以捞刀河为界，设为一类边界类型，边界上各位置的河水位依据水位站的实测数据以及河水位的平均水力坡降进行估算；北部边界设为二类流量边界；上边界取为自由潜水浸润面；底边界取为隔水边界。大气降雨和潜水蒸发作为源汇项处理。模拟区在平面上共划分为44 328个单元、29 175个节点(见图8)。水文地质参数按照岩性分层赋值。模型运行期为10 a。为了节省篇幅，详细模拟过程在此省略，将另文阐述。

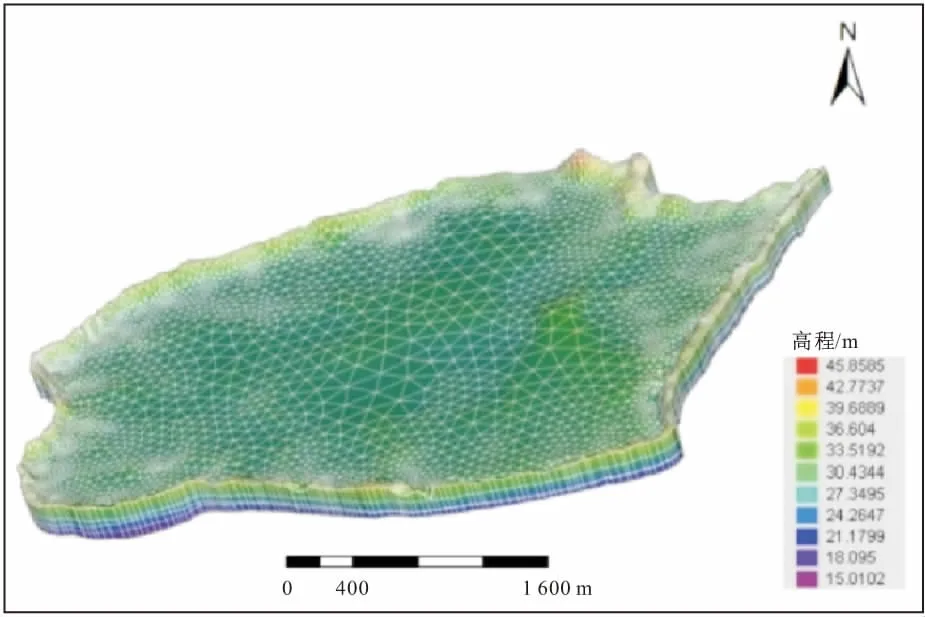
图8 苏托垸地区水库浸没区3D空间离散化示意图Fig.8 3D space discretization diagram of the simulated reservior immersion zone in Sutuoyuan area

本文利用数值法通过数值模拟得到苏托垸地区水库蓄水1 a后、5 a后、10 a后的浸没分区图(见图9至图11)以及水库蓄水10 a后地下水水位剖面图(见图12)。

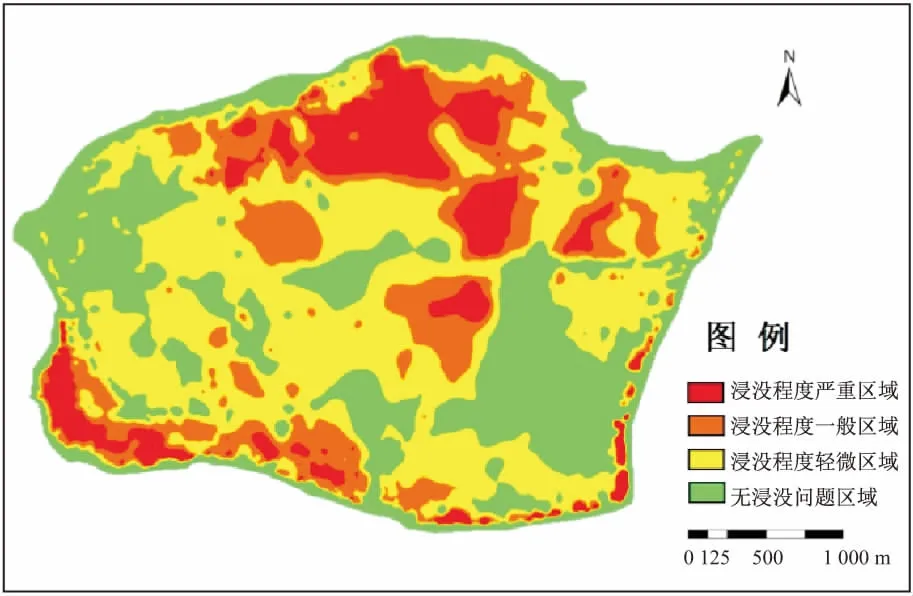
图9 苏托垸地区水库蓄水1 a后的浸没分区Fig.9 Distribution of the immersed zone in Sutuoyuan area 1 a after the impoundment of the reservoir

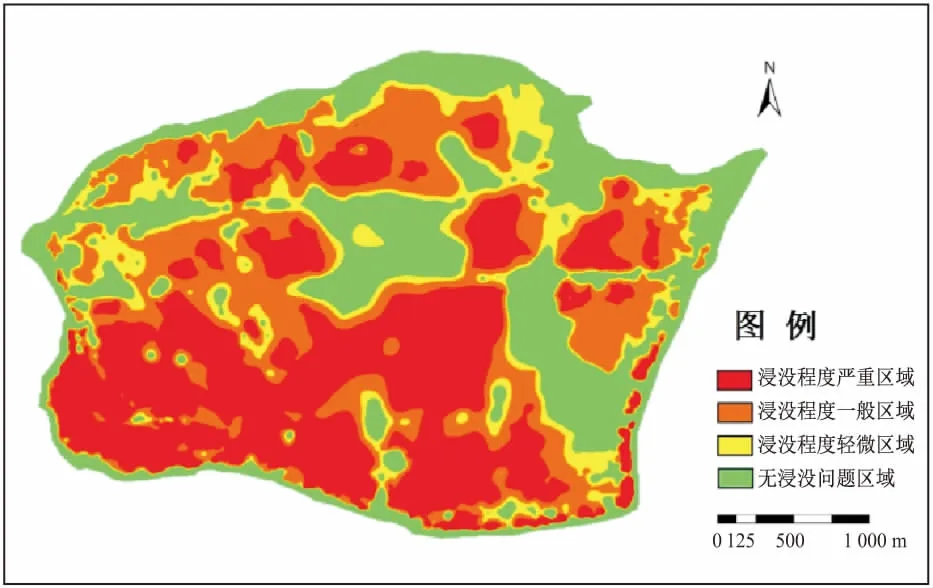
图10 苏托垸地区水库蓄水5 a后的浸没分区Fig.10 Distribution of the immersed zone in Sutuoyuan area 5 a after the impoundment of the reservoir

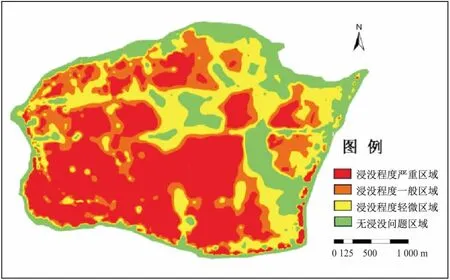
图11 苏托垸地区水库蓄水10 a后的浸没分区Fig.11 Distribution of the immersed area in Sutuoyuan area 10 a after the impoundment of the reservoir

由图9至图12可见，水库蓄水后，研究区内地下水水位明显雍高，并且部分区域地下水水位略高于捞刀河水位,具体表现如下：水库蓄水初期，由于河水位的抬升，地表水补给模拟区地下水，致使区域地下水水位整体抬升，逐渐接近地表，产生浸没灾害；在水库正常蓄水条件下，短期内研究区内出现大范围的轻微浸没灾害，在近岸段浸没程度小，而在远岸段浸没程度反而更大，主要原因可能是水库蓄水前期远岸段地下水水位本身就高，加之区内地下水排泄受阻，因而更早出现浸没现象；水库蓄水5 a时，浸没范围大大增加，浸没面积达70%，其中在研究区内西南部的近岸段浸没程度非常严重，东北部浸没程度最弱;水库蓄水10a后浸没范围基本稳定，浸没面积约占75%，与水库蓄水5 a时浸没情况相比，浸没面积增加不显著，主要集中在浸没程度轻微区。因此，湘江长沙枢纽工程蓄水后，研究区内近岸段浸没程度最严重，远岸段浸没程度最轻；西南部基本都处于浸没状态，而东北部浸没程度最轻。

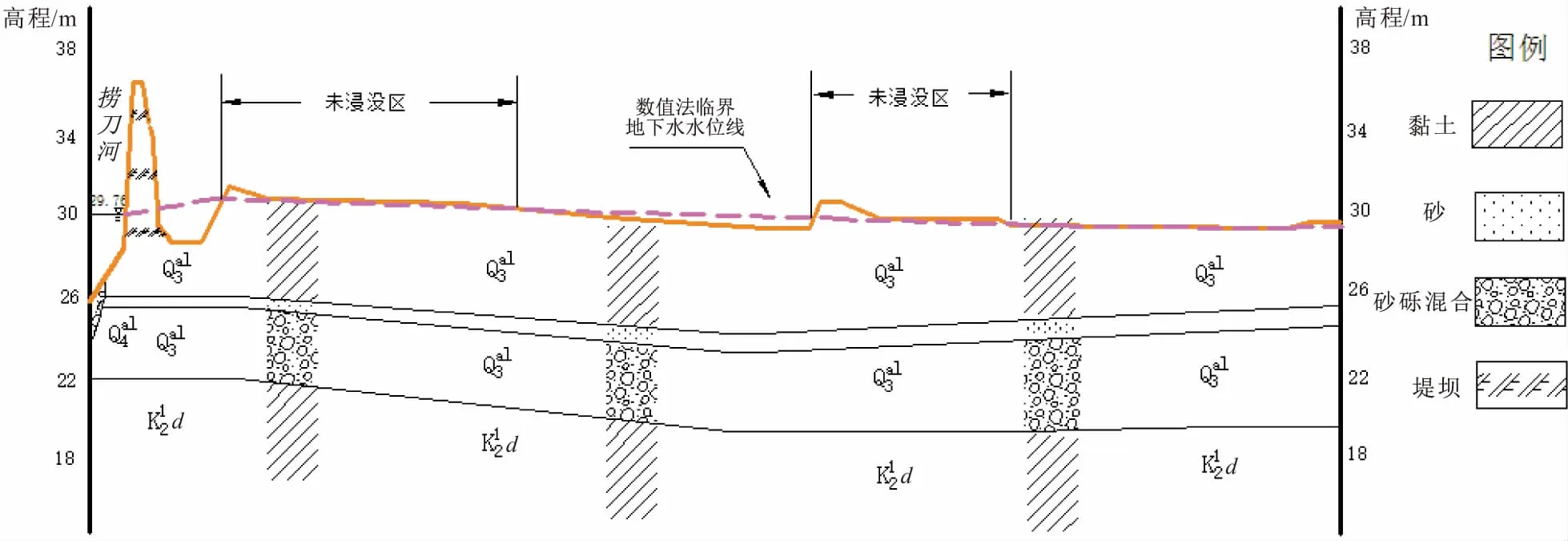
图12 利用数值法预测得到的苏托垸地区地下水水位剖面图Fig.12 Cross section of groundwater level using the numerical method in Shutuoyuan area

3 结论与建议

通过对比3种方法预测得到的苏托垸地区的地下水水位剖面图，可以看出：卡明斯基法预测得到的地下水水位线几乎全部高于地表面，其预测结果是水库蓄水后苏托垸地区均为浸没区；而折减系数法与数值法预测得到的地下水水位线相近，距离捞刀河越近，地下水水位壅高值越大，浸没程度也越大，远离堤坝，地下水水位降低，浸没程度减小，这两种方法预测得到的结果是苏托垸部分地区为浸没区。由此得出以下结论：

(1) 通过上述3种预测方法在具体工程实例中的应用，结果显示卡明斯基法的预测结果偏大，计算得到的地下水水位值偏高超过约1 m。

(2) 在二元结构平原地区进行水库浸没预测时，需要考虑起始水力梯度I0的影响，而考虑起始水力梯度后的折减系数法预测得到的地下水水位线明显低于卡明斯基法的预测结果，且浸没水位变化明显，其预测结果更加合理。

(3)I0的原始定义是“起始水力梯度”，对于这一概念目前尚存争议，但它是折减系数法的理论基础。为了验证I0的存在，应当通过对已建成的水库工程所引发的浸没灾害情况进行重访调查，将实际浸没情况与预测值进行对比，才能得到更加有说服力的证据，并得出更加准确的计算公式或结论。

(4) 解析法(即折减系数法)主要适用于剖面状地下水水位的计算，而数值法适用于浸没灾害的时空变化预测分析。由于二元结构平原地区地下水渗流规律较为复杂，因此采用数值法对该类地区水库浸没进行预测更加准确。

通讯作者：胡 成(1976—)，男，博士，副教授，主要从事工程地质、水文地质和环境水文地质方面的研究。E-mail:hu_cheng@cug.edu.cn