基于改进层次分析法的英山县地质灾害易发性评价
2018-08-08胡致远罗文强晏鄂川谭延嗣
胡致远,罗文强,晏鄂川,谭延嗣
(1.中国地质大学(武汉)工程学院,湖北 武汉 430074;2.中国地质大学(武汉)数学与物理学院,湖北 武汉 430074)
县域地质灾害易发性区划是根据地质灾害发育背景,并参考地质灾害发育现状,以定性分析结合定量评价的方法对县域地质灾害易发性予以确定,它是降低地质灾害损失非常重要的一种非工程措施,其评价结果可科学、经济、有效地为防灾减灾、地质灾害预测预报等工作服务。目前对区域地质灾害易发性进行评价的方法较多[1-3],主要是运用GIS技术[4-5],通过建立相应的灾害数学模型来对地质灾害进行分析与评价。其中,层次分析法因具有高度的逻辑性、系统性、简洁性和实用性而被广泛应用于地质灾害的易发性评价[6]。但传统的层次分析法存在主观性强、计算过程复杂等缺陷,因此本文拟采用改进的层次分析法,在对英山县地质灾害进行详查与综合分析的基础上,通过建立多因素层次结构模型,对该地区地质灾害的易发性进行评价与区划,这对县域的防灾减灾工作具有深远的意义[7]。
1 研究区概况
英山县位于湖北省东部大别山区,地形北东高、南西低,地理坐标在区间115°31′E~116°04′E、30°00′N~31°08′N范围内,其北部大别山主峰向西延伸构成三列山脊,夹东、西两条大河,形成“三山夹两河”的基本轮廓。
英山县属典型亚热带温润季风性气候,年平均降雨量为1 462.0 mm,降雨量逐月分布呈“单峰型”,主要集中于5~8月份,见图1。
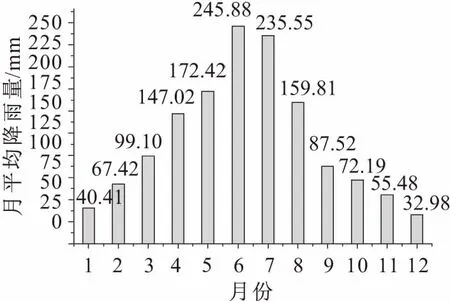
图1 英山县多年月平均降雨量柱状图Fig.1 Histogram of monthly average rainfall in Yingshan County
研究区位于秦岭褶皱系桐柏-大别隆起东段的大别造山带核部,岩浆活动频繁,发生多期变形变质作用,地质构造复杂。英山县域属大别山变质岩区,岩土体类型主要由片岩、片麻岩及侵入花岗岩等组成,表层风化严重,第四系洪-冲积物、残-坡积物等零星分布于河谷和沟谷等地势低洼处。
英山县这种复杂的地形地貌条件、强烈的构造活动、四季分明的气候和水文条件,导致县域内地质灾害十分发育,且地质灾害类型主要表现为滑坡、不稳定斜坡、崩塌。经现场地质灾害详查,研究区共查明地质灾害及隐患点303处,按灾害体体积划分,其以小型地质灾害及隐患点为主。其中,滑坡180处(占59.40%),不稳定斜坡99处(占32.67%),崩塌24处(占7.93%),见表1。滑坡和崩塌作为斜坡失稳的两种形式,其影响因素既有联系又有所差异,对滑坡起控制作用的影响因素同样制约着崩塌的发生,只是各影响因素所起的作用或对不同地质灾害类型的贡献率略有差异。因此,本文在对英山县地质灾害易发性进行评价时,将不稳定斜坡、滑坡和崩塌3种地质灾害类型合并统计。
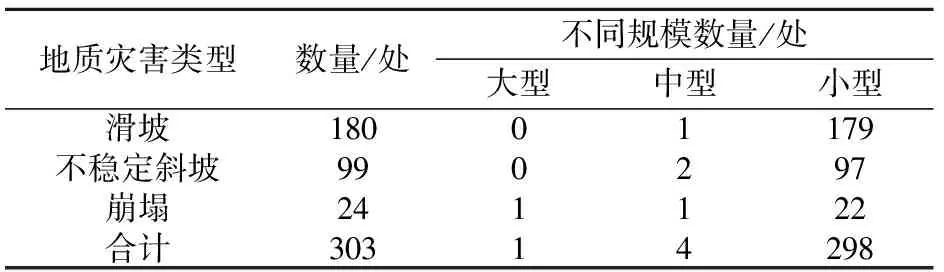
表1 研究区地质灾害及隐患点类型统计结果Table 1 Statistics of the types of potential geological hazard points
2 改进的层次分析法及其应用
2.1 改进层次分析法的基本原理
层次分析法(Analytic Hierarchy Process,AHP)是运筹学家萨蒂于20世纪70年代提出的一种多层次权重的决策分析方法[8]。该方法将实际问题按逻辑性分解为多层次,并比较不同层次各因素之间的关联性,最终求得最底层(指标层)相对于最高层(目标层)的权重关系或优劣次序。
AHP法首先需按层次性对复杂问题进行分解,确定多因素的层次结构模型,并通过传统的九标度法构建一致性或近似一致性的判断矩阵;然后根据相关理论[9],求解判断矩阵的最大特征根及其对应的特征向量,即为下一层因素对于上一层某因素的权重向量。AHP法的具体计算流程见图2。

图2 AHP法的计算流程图Fig.2 Flow chart of AHP
由于AHP法中九标度法的主观性较强,同时在实际应用中往往因反复多次的一致性检验而使计算过程较为繁琐,因此本文拟对AHP法进行改进。改进的层次分析法(Improved Analytic Hierarchy Process,IAHP)具有如下特点:
(1) 降九标度为三标度,以减小人为主观判断模糊性对评价结果的影响。
(2) 通过最优传递矩阵构建判断矩阵,可省略一致性检验的过程,避免了重复性的计算工作。
2.2 改进层次分析法的计算步骤
(1) 基于IAHP法建立地质灾害易发性评价模型。依据AHP法的基本原理,建立多因素层次结构模型,从高至低依次为目标层、准则层、指标层。
(2) 构造比较矩阵A。判断每层因素对上一层某因素的贡献率,采用三标度法对因素进行两两比较,建立对应的比较矩阵A:
该比较矩阵元素Aij表示因素Ai与因素Aj相比的重要性程度,其取值大小见表2。

表2 比较矩阵各元素的取值(三标度法)[10]Table 2 Scales of comparison matrix and their connotations(three-demarcation method)[10]
(3) 计算重要性排序指数ri。由比较矩阵A中各元素相加计算重要性排序指数ri:
(1)
式中:ri表示因素Ai与所有因素的重要性比较结果,其中rmax=max{ri},rmin=min{ri}。
(4) 构造判断矩阵B。根据比较矩阵A构造判断矩阵B,其元素bij遵循下式:
(2)
(5) 构造传递矩阵C。求所构造的判断矩阵B的传递矩阵C,其元素cij遵循下式:
cij=lgbij(i,j=1,2,…,n)
(3)
(6) 构造最优传递矩阵D。求传递矩阵C的最优传递矩阵D,其元素dij遵循下式:
(4)

(5)

(9) 计算指标权重并排序。根据叠乘法,利用上述各层次间计算结果来计算指标权重并排序。例如某一级指标层相对权重为a,对该指标有影响的因素的权重系数分别为(w1,w2,…,wn)T,则这些因素对总目标的影响为awi(i=1,2,…,n),由此可逐步求得指标层各因素对于目标层的影响程度,即指标权重并排序。
2.3 改进层次分析法的应用
2.3.1 地质灾害易发性评价模型的建立
根据野外实地调查的地质灾害情况,将已发生和可能发生地质灾害的地区按不同级别和程度进行划分,即为地质灾害易发性评价与区划。在运用改进的层次分析法进行地质灾害易发性评价时,首先需对实际问题进行层次分析,以构建多因素层次结构模型,这些层次可以分为以下几类:
(1) 目标层:该层为最高层,为所分析的目的或需要解决的问题。本文在地质灾害易发性评价中,以区域地质灾害易发性综合指数A作为目标层。
(2) 准则层:该层为决策时所需考虑的准则。本文根据地质灾害发育现状并结合地质灾害发育背景,综合选取了袭扰指数B1(基于地质灾害发育现状的指标)、致灾基础要素B2、诱发因素B3共三大类因子作为准则层。
(3) 指标层:该层包含了各种致灾的具体影响因素,为决策时需要考虑的指标。本文结合地质灾害发育现状和致灾因素,共选取了灾害点密度、地面平均坡度、地质构造、岩土体类型等13个主要因子作为指标层。
本文基于IAHP法建立的地质灾害易发性评价模型,见图3。

图3 基于IAHP法建立的地质灾害易发性评价模型Fig.3 Evaluation model of susceptibility of geological hazards based on IAHP
2.3.2 构造判断矩阵并求指标权重
判断矩阵体现本层各要素对上一层某因素的贡献率。从准则层开始,分别构建A-B、B-C判断矩阵,如构造B2-C的判断矩阵并求指标权重,其具体步骤如下:
(1) 构造比较矩阵A。将因素C4,C5,…,C11进行两两综合比较,根据地质灾害调查结果,参考实际地区工程实例,并结合专家意见,得出比较矩阵A,并将A中各元素相加求得重要性排序指数ri,其计算结果见表3。
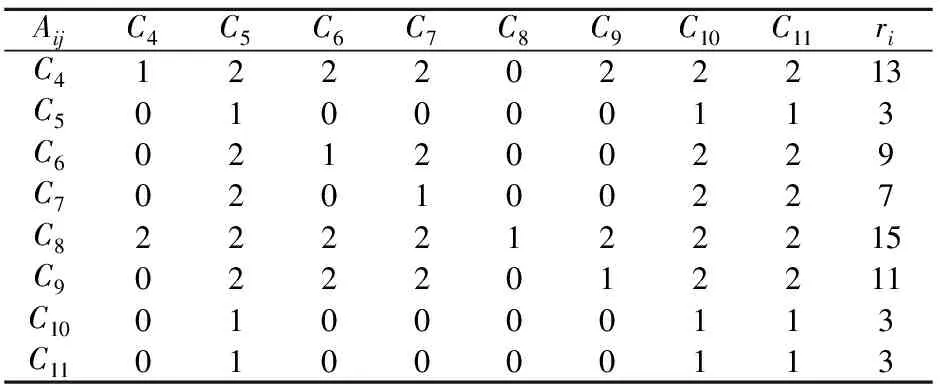
表3 比较矩阵A及重要性排序指数riTable 3 Comparison matrix A and importance sort index ri
由计算结果可知:rmax=max{ri}=15,rmin=min{ri}=3,则km=rmax/rmin=5。
(2) 构造判断矩阵B。利用公式(2),由比较矩阵A求得判断矩阵B为

(3) 构造传递矩阵C。利用公式(3),由判断矩阵B求得传递矩阵C。
(4) 构造最优传递矩阵D。利用公式(4),求得传递矩阵C的最优传递矩阵D。
(5) 构造拟优一致矩阵B′。利用公式(5),求得判断矩阵B的拟优一致矩阵B′。
(6) 采用和积法计算拟优一致矩阵B′的特征向量,即指标层中各基础要素的权重向量WB2为
[(0.217,0.045,0.116,0.084,0.287,0.161,0.045,0.045]T
同理,可分别求出A-B、B1-C、B3-C的拟优一致矩阵的特征向量:
WA=[0.334,0.333,0.333]T
WB1=[0.334,0.333,0.333]T
WB3=[0.750,0.250]T
(7) 利用上述结果,可计算得到指标层各因素对于目标层的权重系数WC为
[0.112,0.111,0.111,0.072,0.015,0.039,0.028,0.096,0.054,0.015,0.015,0.249,0.083]T
由于英山县县域区域范围内地质灾害数量较大,工程地质条件较复杂,因此本文选取了表征地质灾害发育现状的袭扰指数和表征致灾作用的致灾基础要素、诱发因素作为评价因子,对该地区地质灾害易发性进行综合评价。
基于改进的IAHP法通过上述计算已求出各因子的权重,同时将各因子按照不同状态划分为不同的级别,并赋予相应的分级值(见表4),便可建立某个评价单元地质灾害易发性评价的数学模型,即
(6)
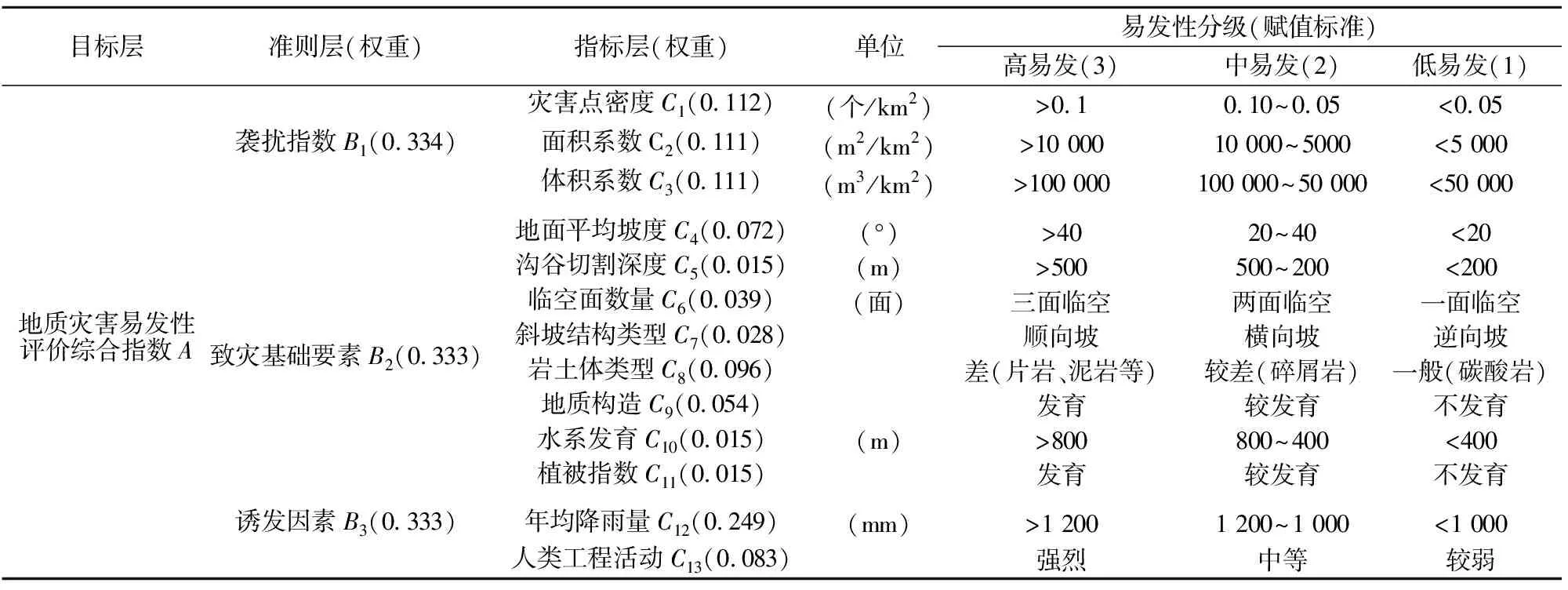
表4 地质灾害易发性判别标准及因子权重Table 4 Discriminant criteria and factor weight of susceptibility of geological hazards
式中:A为某个单元地质灾害易发性评价综合指数;ai为评价因子的权重;ci为致灾因子强度指数。
3 英山县地质灾害易发性综合评价
3.1 地质灾害易发性评价综合指数的计算和分级标准
在建立的地质灾害易发性评价数学模型的基础上,本文运用GIS空间分析工具对英山县域进行单元网格剖分,计算研究区各单元地质灾害易发性评价综合指数A,得到其最高值为2.85,最小值为1.0,该值越高,表示该单元地质灾害易发性越高。
3.2 研究区地质灾害易发性评价与分区
根据计算得到的研究区每个单元地质灾害易发性评价综合指数,本着同类归并的原则,利用自然断点法将研究区内的地质灾害易发性划分为三级:A>2为地质灾害高易发区;A=1.45~2为地质灾害中等易发区;A<1.45为地质灾害低易发区,最后得到研究区地质灾害易发性的综合评价结果,详见图4。

图4 英山县地质灾害易发性分区图Fig.4 Zoning of geological hazard susceptibility in Yingshan County
由图4可见,英山县地质灾害易发性分区将研究区划分为11个区域,地质灾害高易发区主要分布于北部地形较陡区、大别山旅游路线两侧的石头咀镇隘口河村—吴家山森林公园(A1)、草盘地镇西洪村—居民委员会(A2),以及人口居住集中、人类工程活动强烈的红山镇乌云山村—温泉镇蔬菜村(A3)、温泉镇小米畈村—龙潭畈村(A4)4个区域,总面积为269.63 km2,占县域总面积的18.61%;地质灾害中易发区主要分布于西河两岸金家铺镇—石头咀镇(B1)、东河两岸杨家湾镇—陶家河乡(B2)以及县域南部方家咀乡—南河镇(B3),总面积为465.56 km2,占县域总面积的32.13%;地质灾害低易发区主要分布于县域西北(C1)、中部—北东(C2)、西南(C3)、东南(C4)等区域,其总体特征表现为地势平缓、人口密度较小,总面积为713.81 km2,占县域总面积的42.26%。
通过对英山县地质灾害各易发区的分析可知,上述综合评价结果与野外地质灾害调查和定性分析结果基本一致,表明该评价结果具有可靠性。
4 结 论
(1) 英山县地质灾害易发性评价结果表明:地质灾害高易发区面积约为269.63 km2,占县域总面积的18.61%,主要分布在地形较陡区、大别山旅游路线两侧;地质灾害中易发区面积约为465.56 km2,占县域总面积的32.13%,主要分布在东西河两岸;地质灾害低易发区面积约为713.81km2,占县域总面积的42.26%,主要分布在地势平缓地区。
(2) 通过建立地质灾害易发性评价数学模型,采用改进的层次分析法,并运用GIS软件的空间分析功能对英山县地质灾害易发性进行评价与分区,结果表明:该综合评价结果与野外地质灾害调查和定性分析结果基本一致,表明该评价方法在地质灾害易发性评价中具有可靠性,可为该地区防灾减灾、地灾预测预报工作提供参考依据。
通讯作者:罗文强(1963—),男,教授,博士生导师,主要从事数据处理与工程数值计算方面的研究。E-mail:wqluo@cug.edu.cn
