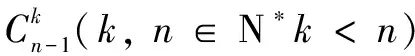基因连锁和交换中性母细胞的类型之规律性
2018-08-07邢德智
邢德智
(陕西省西安市临潼区代王初级中学 710611)
1 基因连锁和交换中性母细胞的类型数组成的杨辉三角

2 连锁和交换中性母细胞类型数组成的杨辉三角的遗传学意义
表1中性母细胞的类型数组成了一个“直角式”的杨辉三角,当“金字塔形”杨辉三角的水平行不变,左斜行变成竖行时,“金字塔形”杨辉三角演变成了“直角式”杨辉三角。在表1中,纵“坐标”表示等位基因的数量,也可看作研究连锁基因的个数;横“坐标”表示随着连锁基因数量的增加,性母细胞可发生的交换次数(不发生交换叫做零交换、发生1次交换叫做单交换、发生2次交换叫做双交换、发生k次交换叫做k交换……)。纵横“坐标”的交点表示该条件下发生交换的性母细胞的类型数。其遗传学意义为:

表1 连锁和交换中性母细胞的类型数
2.1 连锁基因个数与交换次数及最高次交换的关系 随着连锁基因个数n依次递增,性母细胞可交换次数的类型也依次递增。例如,n=2时,只有单交换;n=3时,增加了双交换;n=4时,增加了三交换。当n一定时,该条件下发生的最高次交换为(n-1)交换,且最高次交换类型数只有1种。杨辉三角斜边上的性母细胞类型数1所对应的纵“坐标”为发生该交换的条件,如单交换发生的条件是n≥2,双交换发生的条件是n≥3。所以,n=2时只能研究单交换,即研究1次交换(基因距离测定中,两点试验测不出双交换即为实际验证);n=3时最多研究双交换;以此类推。
2.2 “式算” 当n一定时,n对应的零交换、单交换、双交换、三交换等类型的性母细胞的种类数,可用(a+b)n-1(a=b=1n∈N)计算,即等于这个二项式的各项系数。例如,n=4时,(1+1)4-1=1+3+3+1表示可发生1种零交换、3种单交换、3种双交换、1种三交换,这称为“式算”。“式算”不但能计算出等位基因数n对应的性母细胞类型和数量,而且还揭示了各种不同性母细胞类型数之和等于(1+1)n-1(即2n-1)。由于包括零交换在内的所有类型的性母细胞每种只形成2种配子(零交换形成2种亲本型配子)。所以,不完全连锁遗传中,n对等位基因最多可形成2×2n-1(即2n)种配子。
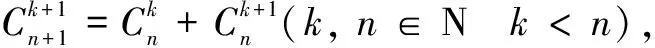
2.4 竖式“图算” 在基因连锁和交换中的性母细胞类型数不仅可以横式“图算”,还可以竖式“图算”。竖式“图算”同样反映出单交换是多交换的基础,但竖式“图算”很直接。例如,由单交换数1,2,3,4可算出双交换数1,3,6,10,……即1(0+1),3(1+2),6(1+2+3),10(1+2+3+4);由双交换数1,3,6,10可算出三交换数1,4,10,20……即1(0+1),4(1+3),10(1+3+6),20(1+3+6+10);由三交换数1,4,10,20可算出四交换数1(0+1),5(1+4),15(1+4+10),35(1+4+10+20)……这便是杨辉三角中斜行与水平行之间的规律性。规律表明:随着等位基因数n依次递增,可交换次数亦即性母细胞类型也依次递增;依次增加的较高次交换的性母细胞类型数也按一定规律递增,其中单交换类型数组成一阶自然数列,双交换类型数组成二阶自然数列,三交换类型数组成三阶自然数列……
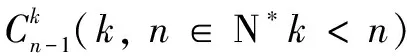
竖式“图算”表现出以下规律性:①零交换(实质是基因完全连锁)是单交换的基础,单交换是双交换的基础,双交换是三交换的基础……即低次交换是相邻高次交换的基础。由于零交换实际上没有交换,所以单交换才是双交换、多交换的最根本的基础。②高次交换的过程重演了所有低次交换的过程。双交换通过两次单交换实现,多交换最终通过多次单交换实现。
3 小结