用于变压器DGA故障诊断的改进PSO优化SVM算法研究

闵亚琪 马鑫 翟振刚 莫家庆 吕小毅

摘 要： 为了提高电力变压器故障诊断的准确率，提出一种基于改进粒子群算法（PSO）优化SVM的变压器故障诊断方法。在对变压器故障进行诊断时采用支持向量机（SVM）与油中溶解气体分析（DGA）相结合的方法，利用PSO对SVM故障诊断模型进行参数寻优，并通过模拟退火算法（SA）改进PSO以提高PSO算法的全局搜索能力。对电力变压器故障诊断的实例分析结果表明，该方法不仅能够有效地进行变压器故障诊断，而且准确率高于传统的变压器故障诊断方法，更适合在变压器故障诊断中应用。

关键词： 变压器； 故障诊断； DGA； 模拟退火算法； 粒子群优化算法； SVM

中图分类号： TN99?34； TP183 文献标识码： A 文章编号： 1004?373X（2018）15?0124?05

Study on SVM algorithm optimized by improved PSO used

for transformer DGA fault diagnosis

MIN Yaqi1， MA Xin2， ZHAI Zhengang3， MO Jiaqing1， 4， L? Xiaoyi1

（1. College of Information Science and Engineering， Xinjiang University， Urumqi 830046， China；

2. Xinjiang Transformer Company， TBEA Co.， Ltd.， Changji 831100， China；

3. Economy and Development Reform Commission， Urumqi High?tech Industrial Development Zone， Urumqi 830011， China；

4. School of Electronic and Information Engineering， Xian Jiaotong University， Xian 710049， China）

Abstract： A transformer fault diagnosis method based on support vector machine （SVM） optimized by improved particle swarm optimization （PSO） algorithm is proposed to improve the fault diagnosis accuracy of electric transformer. The method combining SVM and oil dissolved gas analysis （DGA） is used in the fault diagnosis of transformer. The PSO is adopted to optimize the parameter of SVM fault diagnosis model. The simulated annealing （SA） algorithm is used to improve PSO algorithm and its global search ability. The example analysis results of power transformer fault diagnosis show that the method can diagnose the transformer fault effectively， and its accuracy is higher than that of the traditional transformer fault diagnosis method， which is more suitable for application of transformer fault diagnosis.

Keywords： transformer； fault diagnosis； dissolved gas analysis； simulated annealing algorithm； particle swarm optimization algorithm； support vector machine

0 引 言

电力变压器是输变电系统的核心设备，其在运行过程中性能的好坏直接决定供电系统能否安全稳定运行，一旦变压器在运行过程中发生故障，将造成不可估量的损失，因此及时、准确地诊断出变压器的潛在故障具有重要意义。变压器故障类型有很多，如绝缘导线过热，高湿度、高含气量引起油中低能量密度的局部放电等。随着变压器运行年限的增加，设备自身存在的各种故障隐患如渗漏油、绝缘材料老化、油质不佳、油量过少等会使变压器发生故障的可能性不断增加。电力变压器在长期运行过程中，在放电、过热的情况下绝缘油会发生裂解产生气体，油中溶解气体的体积分数与比值从不同方面较准确地反映出变压器的运行状态。所以国际电工委员会建议检测和诊断油浸电力变压器时，使用油中溶解气体分析（Dissolved Gas Analysis，DGA）的化学检测方法[1]。

近些年，随着智能分类方法的不断发展，在变压器故障诊断方面有越来越多的方法可用来与DGA相结合，如人工神经网络[2?5]、混沌算法[6]、聚类分析[7]及支持向量机 [8?9]（Support Vector Machine，SVM）等。其中，SVM由于可以在小样本的情况下依然保持较好的分类推广能力，且具有适应性强的优点而被广泛研究。但SVM又存在各种各样的缺点，如对缺失数据敏感，现在通用的选择方法在对核函数参数和惩罚因子进行选择时需要花费较长的时间且精度不高等。

为了尽可能地克服以上缺点，本文提出一种基于模拟退火算法（Simulated Annealing，SA）改进粒子群算法（Particle Swarm Optimization，PSO）优化SVM的变压器故障诊断方法。该方法通过PSO算法对SVM故障诊断模型参数进行寻优，而针对PSO算法搜索时容易陷入局部最优的问题，利用SA算法概率突跳的特性加以解决。通过对变压器故障诊断实例进行验证可知，本文采用的变压器故障诊断方法在准确率方面明显优于传统SVM算法、PSO优化的SVM算法。

1 算法基础

1.1 多分类SVM

SVM的标准输出为：

式中：[y∈-1，1]表示负类和正类两类类别；[fx=][ω?x+b]为分类超平面。

由式（1）可知，標准的SVM是一个二类分类器，而多分类SVM即由二分类的SVM推广而来。一般多类分类问题有两种解决方法：一种是直接法，该方法可实现分类目的，但涉及变量过多，计算速度慢，不能广泛应用；另一种是分解?重组法，即将多类别分类问题分解成若干个二分类器的重组，该方法主要有“一对多”分类算法和“一对一”分类算法[10]两种。“一对一”分类算法相较“一对多”分类算法虽然在应用到类别数较高的分类时，判断速度会降低，但在训练阶段所用的总时间少得多，且分类准确度也较高。本文涉及的变压器故障状态为7类，所以选用在类别数较低时耗时少、精度高的“一对一”分类算法SVM。该方法对有[k]个类别的样本进行分类时，会构造出[k（k-1）2]个标准的二类分类器，从而实现对任意不同的两类样本间的分类。当对一个未知样本进行分类时，各二类分类器对其判断出的类别进行投票，得票最高者即为该未知样本最终被判断出的类别[11]。

1.2 基于改进PSO算法优化SVM的变压器故障诊断

1.2.1 SA算法

SA算法最早的思想是由N.Metropolis等人提出[12]，后来S.Kirkpatrick等成功地将退火思想引入到组合优化领域，提出了SA算法。对于SA算法，当前最优的状态依然存在被其他非最优状态取代的可能性，因此可以跳出局部最优。

本文采用温度线形下降的方法处理控制参数[T]：

式中：[λ]为退火常数，[0<λ<1]。因此[Ti+1

标准SA算法的具体流程如图1所示[13]，[f]为目标函数。

1.2.2 改进的PSO算法

PSO算法[13]具有复杂度较低，计算形式简单，同时能够保证算法模型的最终收敛精度较高的优点[14]。

在标准PSO算法公式中规定[vi（k）]为第[k]步迭代的速度，[xi（k）]为第[k]步迭代的位置，则第[k+1]步的[vi（k+1）]和[xi（k+1）]为：

式中：[i=1，2，…，m]；[ω]为惯性权重；[r1]与[r2]能够在[0，1]内任意取值；[pi=pi1，pi2，…，piN]与[pg=pg1，pg2，…，pgN]分别为每个粒子和整个种群迄今能搜到的最优位置；[c1]与[c2]为学习因子[15]。

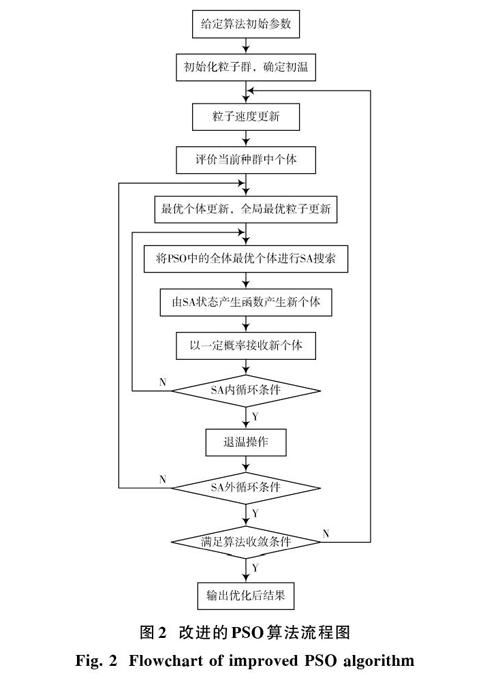
为克服PSO算法容易陷入局部极值的缺陷，将PSO算法与SA算法结合，通过SA算法以一定概率接受劣解的特点使PSO算法跳出局部极值点。改进的PSO算法流程[16]如图2所示。

1.2.3 基于改进PSO和SVM的故障诊断模型

SVM的惩罚因子C和核函数参数g会很大程度的影响其分类精度和泛化能力，并且现在通用的参数选择方法存在耗时长且精度不高的缺陷，因此为了能够为SVM提供最优的参数，亟需找到一种更加高效的方法。本文根据PSO算法运算速度快及搜索能力强的特点，提出将改进后的PSO与SVM相结合的故障诊断方法来寻找SVM故障诊断模型的最优参数以提高变压器故障诊断的准确度。电力变压器故障诊断模型分为DGA数据搜集，数据预处理，利用改进的SAPSO算法构造SVM的变压器故障诊断模型，对故障类型进行分析并显示结果四步。

2 实例分析

2.1 特征向量的提取

本文所用DGA数据为文献[9]中的变压器故障特征气体样本值，共有177组样本数据。其中故障诊断的特征量为变压器油中溶解的气体含量，选取主要的五类气体，即C2H6（乙烷）、C2H4（乙烯）、CH4（甲烷）、C2H2（乙炔）、H2（氢气）。为了降低量值差异对分类可能造成的影响，对数据做归一化处理。变压器故障诊断的训练样本有126组样本数据，测试样本有51组样本数据，表1为变压器故障诊断样本统计表，其中正常情况也算在内共有7种状态。

2.2 故障诊断结果分析

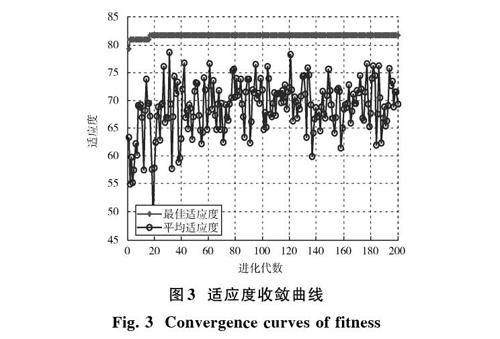
1） SAPSO优化算法对SVM故障诊断模型进行参数优化后的适应度收敛曲线如图3所示，横轴表示进化代数，纵轴表示适应度，模型的最优参数为：[C=]86.618 9，g=12.140 8。两曲线分别表示种群中全部粒子在每代中的平均适应度值和最大适应度值的变化规律[17]。由图3能够分析出，在最初的12代中曲线收敛的速度相对较快，之后随着进化代数的增加，曲线收敛速度明显变慢，曲线逐渐平稳并接近一致，所以该方法达到了SVM参数选优的目的。

2） 用本文提出的SAPSO优化的SVM算法诊断变压器故障。学习因子[c1]初始值为1.5，[c2]初始值为1.7，最大进化数量初始值为200，种群最大数量初始为20个粒子，SVM 参数C的变化范围为[0.01，100]，SVM 参数g的变化范围为[0.001，1 000]，初始温度为100 ℃，退火常数[λ]为0.7。测试集的实际分类和预测分类如图4所示，横轴表示测试集样本，纵轴表示类别标签，51组样本中仅有5组（1组正常状态、1组低温过热、1组中温过热、1组局部放电及1组高能放电）诊断出错，测试的故障诊断准确率为90.196 1%，所以采用该方法进行电力变压器故障诊断是有效的。

3） 分别用传统SVM算法、PSO优化的SVM算法与SAPSO优化的SVM算法诊断变压器故障。用SVM对故障进行诊断时，令C=2，g=1。为公平起见，后两种算法除了C和g外的参数设置均相同。变壓器故障诊断分类结果如表2所示。从表2中能看出，SVM算法的准确率最低，为43.137 3%；PSO优化的SVM算法准确率为84.313 7%；SAPSO优化的SVM算法精确度最高，为90.196 1%。

3 结 论

根据上述实例分析，可得出如下结论：

1） 本文所用的SAPSO算法利用SA算法以一定概率接受劣值的特点，实现PSO算法中粒子位置的变异，使种群多样性得以保持，避免了PSO算法陷入局部最优的危险，从而提高了PSO算法的优化效率及全局寻优能力。

2） 针对SVM参数选取困难、需要试凑的问题，给出改进后的PSO算法与SVM结合的方法，即利用SAPSO算法对SVM的参数进行寻优。

3） 变压器故障诊断试验证明，本文提出的SAPSO?SVM法可以有效地对变压器故障进行诊断，且比PSO?SVM法、SVM法具有更高的故障诊断准确率。

注：本文通讯作者为吕小毅。

参考文献

[1] DUVAL M， DE PABLO A. Interpretation of gas in oil analysis using new IEC publication 60599 and IEC TC 10 databases [J]. IEEE electrical insulation magazine， 2001， 17（2）： 31?41.

[2] TRIPATHY M， MAHESHWARI R P， VERMA H K. Power transformer differential protection base on optimal probabilistic neural network [J]. IEEE transactions on power delivery， 2010， 25（1）： 102?112.

[3] ZHANG Y， DING X， LIU Y， et al. An artificial neural network approach to transformer fault diagnosis [J]. IEEE transactions on power delivery， 1996， 11（4）： 1836?1841.

[4] 陈伟根，潘翀，云玉新，等.基于小波网络及油中溶解气体分析的电力变压器故障诊断方法[J].中国电机工程学报，2008（7）：121?126.

CHEN Weigen， PAN Chong， YUN Yuxin， et al. Power transformer fault diagnosis method based on wavelet network and dissolved gas analysis in oil [J]. Proceedings of the CSEE， 2008（7）： 121?126.

[5] MENG K， DONG Z Y， WANG D H， et al. A self?adaptive RBF neural network classifier for transformer fault analysis [J]. IEEE transactions on power systems， 2010， 25（3）： 1350?1360.

[6] 公茂法，柳岩妮，王来河，等.基于混沌优化粒子群BP神经网络的电力变压器故障诊断[J].电测与仪表，2016，53（15）：13?16.

GONG Maofa， LIU Yanni， WANG Laihe， et al. Power transformer fault diagnosis based on chaotic optimized particle swarm BP neural network [J]. Electrical measurement & instrumentation， 2016， 53（15）： 13?16.

[7] 李赢，舒乃秋.基于模糊聚类和完全二叉树支持向量机的变压器故障诊断[J].电工技术学报，2016，31（4）：64?70.

LI Ying， SHU Naiqiu. Transformer fault diagnosis based on fuzzy clustering and complete binary tree SVM [J]. Transactions of China electrotechnical society， 2016， 31（4）： 64?70.

[8] VAPNIK V N. The nature of statistical learning theory [M]. New York： Springer Verlag， 1995.

[9] 刘义艳，陈晨，亢旭红，等.基于支持向量机的变压器故障诊断[J].现代电子技术，2011，34（24）：118?120.

LIU Yiyan， CHEN Chen， KANG Xuhong， et al. Transformer fault diagnosis based on SVM [J]. Modern electronics technique， 2011， 34（24）： 118?120.

[10] 张明慧.基于DGA的变压器故障诊断算法研究[D].淮南：安徽理工大学，2013.

ZHANG Minghui. Research on transformer fault diagnosis algorithm based on DGA [D]. Huainan： Anhui University of Science & Technology， 2013.

[11] 仲元昌，万能飞，夏艳，等.基于油气参数分析的电力变压器故障分步式诊断算法[J].高电压技术，2014，40（8）：2279?2284.

ZHONG Yuanchang， WAN Nengfei， XIA Yan， et al. Stepwise diagnosis algorithm of power transformer fault based on analysis of oil and gas parameters [J]. High voltage enginee?ring， 2014， 40（8）： 2279?2284.

[12] STEINBRUNN M， MOERKOTTE G， KEMPER A. Heuristic and randomized optimization for the join ordering problem [J]. The VLDB journal， 1997， 6（3）： 8?17.

[13] 吕丹，童创明，钟卫军.基于粒子群和模拟退火算法的混合算法研究[J].计算机工程与设计，2011，32（2）：663?666.

L? Dan， TONG Chuangming， ZHONG Weijun. Hybrid algorithm research based on particle swarm optimization and simulated annealing algorithm [J]. Computer engineering and design， 2011， 32（2）： 663?666.

[14] 冯一博.基于粒子群思想改进支持向量机优化算法的研究[D].哈尔滨：哈尔滨理工大学，2013.

FENG Yibo. Research on improvement of SVM optimization algorithm based on particle swarm optimization [D]. Harbin： Harbin University of Science and Technology， 2013.

[15] KENNEDY J， EBERHART R. Particle swarm optimization [C]// Proceedings of 1995 IEEE International Conference on Neural Networks. [S.l.]： IEEE， 1995： 1942?1948.

[16] 杨光友.混合粒子群优化及其在嵌入式智能控制中的应用[D].武汉：武汉理工大学，2006：22?62.

YANG Guangyou. Hybrid particle swarm optimization and its application in embedded intelligent control system [D]. Wuhan： Wuhan University of Technology， 2006： 22?26.

[17] 郑含博，王伟，李晓纲，等.基于多分类最小二乘支持向量机和改进粒子群优化算法的电力变压器故障诊断方法[J].高电压技术，2014，40（11）：3424?3429.

ZHENG Hanbo， WANG Wei， LI Xiaogang， et al. Power transformer fault diagnosis method based on multi class least squares SVM and improved particle swarm optimization algorithm [J]. High voltage engineering， 2014， 40（11）： 3424?3429.