最小二乘拟合的蒙特卡罗移动定位算法研究

谭志 梁丽文 夏磊

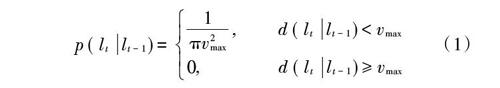
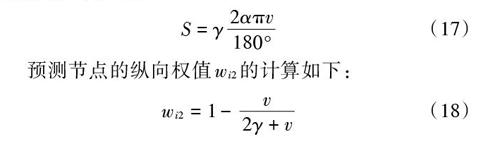
摘 要： 针对传统蒙特卡罗定位算法由于节点采样效率低导致的定位精度低、定位不准确的缺陷，提出一种改进的最小二乘拟合蒙特卡罗（LSFMCL）定位算法。该算法利用MBC算法优化采样空间，并利用最小二乘拟合节点运动轨迹，对节点位置进行预测，进一步得到最优采样区域，最后提出权值概念并利用预测节点的权值信息计算未知节点的位置。仿真结果表明，与传統算法相比，优化后的算法提升了节点的采样率，提高了定位精度，对于移动节点的定位具有更加广泛的应用前景。

关键词： 蒙特卡罗定位算法； MBC算法； 最小二乘法拟合； 移动节点定位； 运动轨迹； 权值概念

中图分类号： TN911.1?34； TP212.9 文献标识码： A 文章编号： 1004?373X（2018）15?0010?06

Research on least squares fitting Monte Carlo localization algorithm for mobile nodes

TAN Zhi， LIANG Liwen， XIA Lei

（College of Electrical and Information Engineering， Beijing University of Civil Engineering and Architecture， Beijing 100044， China）

Abstract： The traditional Monte Carlo localization algorithm has the defects of low positioning precision and inaccurate positioning due to the low efficiency of node sampling. Therefore， an improved least squares fitting Monte Carlo localization （LSFMCL） algorithm is proposed. The algorithm is adopted to optimize the sampling space by taking advantage of MBC algorithm， fit the node motion trajectory with least square method to predict the location of nodes， and then obtain the optimal sampling area. The weight concept is proposed to calculate the location of the unknown node by using the weight information of the predicted node. The simulation results show that， in comparison with traditional algorithm， the optimized algorithm can improve the sampling rate of the node and positioning accuracy， and has wider application prospect for the localization of the mobile nodes.

Keywords： Monte Carlo location algorithm； MBC algorithm； least square fitting； mobile node localization； motion trajectory； weight concept

0 引 言

无线传感器网络技术（Wireless Sensor Networks，WSN）作为21世纪发展的热点，具有很多别的技术所没有的优点，如监测范围广、运行成本低、网络自组织性好等。目前，传感器网络广泛地应用在智能家居、建筑防火、环境监测、军事侦察等领域[1]。

WSN技术的节点定位主要是指已知自身位置的节点通过某种测量方法来定位未知节点位置的方法。因此作为WSN热门技术之一的节点定位算法有不同的分类标准。根据是否需要测距分为基于测距的定位算法和无需测距的定位算法。典型的基于测距的定位算法包括TOA（Time of Advent）定位算法[2]、TDOA（Time Difference Of Arrival）定位算法[3]、 RSSI（Received Signal Strength Indication）定位算法[4]、AOA（Angle of Arrival）定位算法[5]等，而典型的无需测距的定位算法包括质心算法[6]、DV?Hop 算法[7]、Amorphous 算法[8?9]、APIT 算法[10]等。根据WSN中传感器节点是否能够移动，节点的定位算法分为静态定位（Static Localization）和动态定位（Dynamic Localization）两种类别。目前对于传统静态WSN的定位技术方面已有不少典型的算法，如质心定位算法[11]、凸规划定位算法[12]、SPA相对定位算法[13]等都是静态定位算法。但是由于实际应用中，大多数的节点都是运动的，传统的静态节点定位不能捕捉到节点的运动，会造成很大的定位误差。因此，如何定位移动节点成为WSN技术的一个热点。

MCL（Monte Carlo Localization）[14]定位算法是最早提出定位移动节点的一种算法，也是最典型的一种移动节点定位方法。但是这种算法对采样数据要求太高，进而提出MBC算法[15]。MBC算法对粒子采样空间进行了有效优化，但是锚节点较少时，误差仍然较大。

利用最小二乘拟合的蒙特卡罗移动定位算法不仅通过MCB算法来获取历史节点，减少算法初始误差；同时还能预测移动节点的运动轨迹，降低采样次数，提高采样率。

1 蒙特卡罗定位算法

1.1 蒙特卡罗定位算法

蒙特卡罗定位算法是用来表示感知与运动的概率模型的粒子滤波过程，能在复杂网络定位中較精准定位。定位阶段包括预测和滤波。预测阶段是根据节点的速度信息和在前一定位时刻的粒子集信息来确定采样区域，并随机釆样得到粒子位置信息[16]。滤波阶段通过锚节点信息对预测阶段得到的粒子进行筛选，舍弃不满足条件的粒子，并且记录能够符合滤波条件的粒子，然后利用它们的均值来估计节点的位置。如果滤波后的粒子数不能满足定位所需粒子的数目，就需要执行重采样与滤波过程，直到得到足够的粒子数或者釆样次数到达最大为止[17]。

1.2 蒙特卡罗定位算法内容

MCL算法定位阶段包括预测和滤波，节点移动方式按照随机行走模型（Random Walk Model，RWM）进行，RWM模型是移动WSN最常见的运动模型之一。在RWM模型中，节点速度和位置都是未知的，仅有节点最大运动速率[vmax]已知，并且方向不确定。假设上一时刻的节点粒子集为[lt-1]，则目前时刻的节点可能位置存在于以[lt-1]为圆心，以[vmax]为半径的圆内。其中目前时刻的粒子集为[lt]。用[d（l1，l2）]表示两个点[l1]，[l2]之间的欧几里德距离，且节点速率在[[0，vmax]]之间满足均匀分布，则状态转移概率密度函数[p（ltlt-1）]为：

[p（ltlt-1）=1πv2max，d（ltlt-1）

预测阶段得到的集合[R]中的粒子，是从以[lt-1]为圆心，以[vmax]为半径的圆形区域中随机选择出来的。这时的预测结果非常不精确，需要进行滤波。

在滤波阶段，可以依据新的观测信息，滤除掉满足网络连通度条件的样本。文献[18]给出了粒子滤波条件：

[filter（l）=?s∈S，d（l，s）≤r∧?s∈T，r

式中：r是通信半径；[s]为锚节点集合。假如得到的位置样本符合滤波条件，那么状态转移概率分布[p（ltlt-1）]函数的值为1，反之为0。

2 MCB定位算法

MCB算法是在 MCL算法基础上提出的。相对于 MCL，MCB算法采用蒙特卡罗盒子采样，有效改进了样本区域。锚盒子采样区间为：

[xmin=max（xi-di）ymin=max（yi-di） xmax=max（xi+di）ymax=max（yi+di） ] （3）

为了提高采样区域的利用率，历史节点的获取通过由DV?Hop辅助的MCB算法来实现。作为一种非测距定位算法，DV?Hop算法主要根据网络连通度进行节点间的计算。为了提高蒙特卡罗定位算法精度，采用了DV?Hop测距方法。

2.1 DV?Hop定位算法测距

DV?Hop测距步骤如下：

首先已知位置的锚节点向四周发射信号，使得锚节点的位置可以被周围节点获取。周围节点如果通过1跳能获取锚节点信息，记跳数为1，并向周围转发信息，如果节点通过多次转发邻节点信息后，跳数记最小值。

根据锚节点与锚节点的距离和跳数计算出跳距，然后根据未知节点和锚节点的距离及跳距计算出它们的距离[19]。跳距公式为：

[HopSizei=（xi-xj）2+（yi-yj）2hij] （4）

已知[n]个锚节点位置[xi=（xi，yi）（i=1，2，…，n）]，未知节点[x=（x，y）]与参考节点之间距离为[ri（i=1，2，…，n）]，得到：

[（x1-x）2+（y1-y）2（x2-x）2+（y2-y）2? （xn-x）2+（yn-y）2=r21r22?r2n] （5）

变换得到：

[Ax=b] （6）

则[A]与[b]分别为：

[A=2（xn-x1）2（yn-y1）2（xn-x2）2（yn-y2）??2（xn-xn-1）2（yn-yn-1）] （7）

[b=r21-r2n-x21-y21+x2n+y2nr22-r2n-x22-y22+x2n+y2n?r2n-1-r2n-x2n-1-y2n-1+x2n+y2n] （8）

对于计算[（x，y）]的位置，最小二乘算法能够解决这类问题，使用式（9）进行计算：

[x=（ATA）-1ATb] （9）

2.2 MCB定位算法

通过式（9）计算出[（x，y）]，并进行[di]的计算：

[di=（xi-xj）2+（yi-yj）2] （10）

最后，通过传统MCB采样滤波得到节点估值位置。

3 最小二乘法拟合的蒙特卡罗定位算法

3.1 最小二乘拟合的基本原理

最小二乘法又被称作最小平方法（ Least Square Method），是一种数学优化技术。最小二乘法能够容易地得到未知数据的值，并能使数据实际值与计算值的差的平方和达到最小。此外最小二乘法用于曲线拟合可以使各种应用更贴合实际[20]。

对于给定的一组数据[（xi，yi）]（i=0，1，2，…，m），要求在函数空间[Φ=spanφ0，φ1，φ2，…，φn]能够找到一个函数[y=S*（x）]，使误差平方和最小：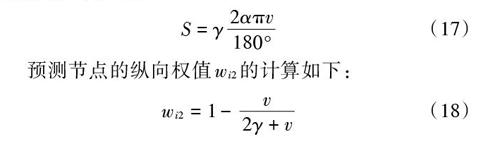

[σ22=i=0mσ2=i=0mS?（xi）-yi2=i=0mS（xi）-yi2] （11）

式中：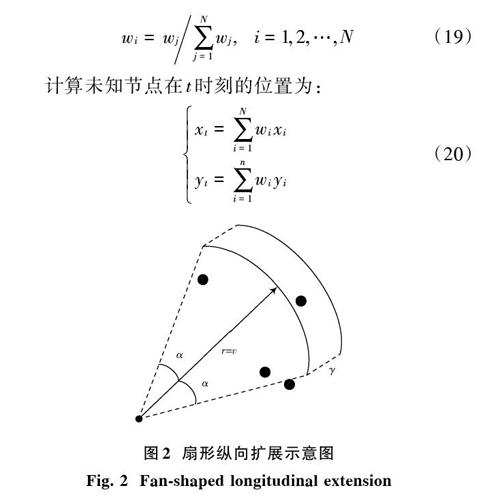

[S（x）=a0φ0（x）+a1φ1（x）+…+anφn（x）] （12）

3.2 运动趋势的预测

假设节点平滑的、连续的运动，通过节点历史位置信息，利用最小二乘拟合的方法预测节点运动趋势。LSFMCL（Least Squares Fitting Monte Carlo）定位算法中每个节点都保留着原来前三个时刻位置信息，通过已有历史位置信息预测移动节点的运动趋势。当新的位置信息产生后，将前三个时刻最早的位置信息替换掉，以此来不断更新节點最新的三个历史位置。假设节点前三个时刻[t1，t2，t3]（其中[t1

[xt=f（t）yt=g（t）] （13）

假设函数偏导数存在，即节点运动是平滑的并且连续的，对式（13）求偏导数，得到节点在t时刻x轴[y]轴方向的预测运动速度：

[vx=df（t）dtt=tn-1vy=dg（t）dtt=tn-1] （14）

由式（14）得到节点在t时刻的运动速度及方向：

[v=v2x+v2yα=arctanvyvx] （15）

根据节点的运动趋势，在选择预测的节点位置时首先以式（15）得到的节点运动速度[v]为半径，以前一时刻的节点位置为圆心，以前一时刻的速度方向顺时针和逆时针各展开[α+β]，满足[α+β<π]，得到一个扇形。然后，随机抽取位于扇形[N]个点作为预测点，其中越靠近预测的速度矢量，预测精度越高，称为较优预测点。

3.3 节点位置计算

由图1可知，在[α]角度附近的预测点的权值要比其他地方的预测点的权值高。预测节点的扇形横向权值[wi1]的计算如下：

[wi1=1-βα+β] （16）

如果经过滤波后能够得到符合要求的预测点小于[N]，且扇形的夹角不宜再变大，则此时向扇形速度方向扩展，称为扇形纵向权值。假设拓展宽度为[γ]，如图2所示，同时由于[α]较小，所以速度方向拓展部分可以看作是矩形，面积为[S]：

[S=γ2απv180°] （17）

预测节点的纵向权值[wi2]的计算如下：

[wi2=1-v2γ+v] （18）

当得到所有的权值以后，对权值进行归一化处理，使得所有权值相加其和为1。

[wi=wjj=1Nwj， i=1，2，…，N ] （19）

计算未知节点在t时刻的位置为：

[xt=i=1Nwixiyt=i=1nwiyi ] （20）

4 仿真及结果分析

无线传感器网络连通度可以体现网络鲁棒性的好坏，是评估网络结构的重要指标[21]。假设未知节点估计位置为（[xi]，[yi]），（[Xi]，[Yi]）表示待测节点实际位置，未知节点总数为[un]，定位误差用[errori]表示。

误差[errori]计算公式为：

[errori=（Xi-xi）2+（Yi-yi）2] （21）

平均定位误差[e]计算公式为：

[e=errorun] （22）

假设节点分布在200 m×200 m的区域内，在此区域中均匀分布锚节点，节点移动方式按照RWM模型进行，所有节点的通信半径为[r=25] m，移动节点最大速度[vmax≤2 m/s]，运动方向未知，采样的节点数为[N=200]。考虑到通信半径对定位误差的影响，分别取通信半径为[r=25] m和[r=20] m，在不同的通信半径下，所有待测节点的误差图如图3所示。节点移动速度影响定位误差，一般移动速度越大，定位误差越大。

如图3所示，当速度不同时，LSFMCL定位算法与MCB算法和传统算法定位误差的比较，LSFMCL定位算法明显优于其他算法，此外当移动节点运动速度小于一定值时误差随速度增大有减小趋势但变化不大，当移动节点速度超过一定值时，定位误差逐渐增大。同时，对比不同的通信半径的影响，r=20 m的误差显然小于r=25 m时的平均定位误差。

图4表现了随着网络连通度的提高，无线传感器网络定位误差减小。仿真结果表明，在同样的网络连通度下，LSFMCL定位算法优于MCB算法，传统的MCL算法最差。网络连通度超过一定值时，定位误差趋于稳定。

锚节点与定位误差的关系如图5所示，锚节点越多，定位误差越小，定位精度越高，并且当锚节点数达到一定的值后，定位误差趋于稳定。

如图6所示，锚节点数对样本采样次数的影响很小，因为LSFMCL定位算法对节点运动进行了有效预测，有效地捕捉到节点运动方式，使得采样次数大幅度减少，提高了运行效率，节省了运行时间。

5 结 语

改进后的算法从传统定位算法误差产生的原因出发，利用最小二乘拟合的算法预测节点运动趋势，确定采样区间，在一定范围内提高了预测节点的有效率；并提出权值概念，根据预测节点距离运动方向[α]的远近确定权值，进而计算出未知节点的位置。从实验结果得出，传统的MCL算法误差太大，MCB定位误差相比传统MCL，定位精度和采样率虽然有很大提高，但是采样次数仍然很高，利用最小二乘拟合的算法预测节点运动趋势的LSFMCL定位算法定位精度最高，鲁棒性最好，可以被广泛应用。

参考文献

[1] DU Xiaoyu， SUN Lijuan， XIAO Fu， et al. Localization algorithm based on minimum condition number for wireless sensor networks [J]. Journal of electronics （China）， 2013， 30（1）： 25?33.

[2] 姜志鹏，陈正宇，刘影，等.TOA定位算法非线性优化问题研究[J].传感技术学报，2015，28（11）：1716?1719.

JIANG Zhipeng， CHEN Zhengyu， LIU Ying， et al. TOA positioning algorithm nonlinear optimization problem research [J]. Chinese journal of sensors and actuators， 2015， 28（11）： 1716?1719.

[3] 张健，李鸥.改进的无线传感器网络TDOA定位算法[J].计算机工程与应用，2010，46（16）：171?120.

ZHANG Jian， LI Ou. Improved wireless sensor network TDOA positioning algorithm [J]. Computer engineering and applications， 2010， 46（16）： 171?120.

[4] 谭志，张卉.无线传感器网络RSSI定位算法的研究与改进[J].北京邮电大学学报，2013，36（3）：88?91.

TAN Zhi， ZHANG Hui. Research and improvement of RSSI localization algorithm in wireless sensor networks [J]. Journal of Beijing University of Posts and Telecommunications， 2013， 36（3）： 88?91.

[5] 诸燕平，黄大庆， 李勃.基于AOA的无线传感器网络节点定位算法[J].传感器与微系统，2010，29（1）：98?101.

ZHU Yanping， HUANG Daqing， LI Bo. AOA based wireless sensor network node localization algorithm [J]. Sensor and micro system， 2010， 29（1）： 98?101.

[6] 刘皇保，王涛，彭刚.一种改进的质心定位算法[J].微型机与应用，2013，32（11）：73?75.

LIU Huangbao， WANG Tao， PENG Gang. An improved centroid localization algorithm [J]. Microcomputers and applications， 2013， 32（11）： 73?75.

[7] 卫开夏，田金鹏，王克谦.无线传感器网络 DV?Hop定位改进算法[J].传感技术学报，2010，23（12）：1820?1824.

WEI Kaixia， TIAN Jinpeng， WANG Keqian. Improved DV?Hop localization algorithm for wireless sensor networks [J]. Chinese journal of sensors and actuators， 2010， 23（12）： 1820?1824.

[8] NAGPAL R， SHROBE H， BACHRACH J. Organizing a global coordinate system from local information on an Ad Hoc sensor network [J]. Information processing in sensor networks， 2003， 2634： 333?348.

[9] 安文秀，赵菊敏，李灯熬.基于Amorphous的无线传感器网络定位算法研究[J].传感器与微系统，2013，32（2）：33?35.

AN Wenxiu， ZHAO Jumin， LI Dengao. Research on location algorithm of wireless sensor network based on Amorphous [J]. Sensor and microsystem， 2013， 32（2）： 33?35.

[10] 冯秀芳，崔秀锋，祈会波.无线传感器网络中基于移动锚节点的APIT的改进定位算法[J].传感技术学报，2011，24（2）：269?274.

FENG Xiufang， CUI Xiufeng， QI Huibo. An improved loca?lization algorithm for APIT based on mobile anchor nodes in wireless sensor networks， Journal of [J]. Chinese journal of sensors and actuators， 2011， 24（2）： 269?274.

[11] 李文辰，张雷.无线传感器网络加权质心定位算法研究[J].计算机仿真，2013，30（2）：191?194.

LI Wenchen， ZHANG Lei. Weighted centroid localization algorithm in wireless sensor networks [J]. Computer simulation， 2013， 30（2）： 191?194.

[12] 任克强，庄放望.移动锚节点凸规划定位算法研究及改进[J].传感技术学报，2014，27（10）：1406?1411.

REN Keqiang， ZHUANG Fangwang. Research on mobile anchor node convex programming and location algorithm and improvement [J]. Chinese journal of sensors and actuators， 2014， 27（10）： 1406?1411.

[13] 苏进，万江文，于宁.无线传感器网络相对定位算法研究[J].传感技术学报，2007，20（12）：2695?2700.

SU Jin， WAN Jiangwen， YU Ning. Relative location algorithm for wireless sensor networks [J]. Chinese journal of sensors and actuators， 2007， 20（12）： 2695?2700.

[14] 梅举，陈涤，辛玲.基于蒙特卡洛方法的移动传感网节点定位优化算法[J].传感技术学报，2013，26（5）：689?694.

MEI Ju， CHEN Di， XIN Ling. Based on Monte Carlo method for mobile sensor network node localization optimization algorithm [J]. Chinese journal of sensors and actuators， 2013， 26（5）： 689?694.

[15] 张锐恒，庄毅，赵振宇，等.基于MCB的传感网移动目标定位算法[J].计算机科学，2012，39（8）：34?37.

ZHANG Ruiheng， ZHUANG Yi， ZHAO Zhenyu， et al. MBC based sensor network moving target localization algorithm [J]. Computer science， 2012， 39（8）： 34?37.

[16] 陈冰洁，黄小平，王岩.基于MDS技術与MCL方法的无线传感器网络移动节点定位算法[J].微型机与应用，2011，30（6）：88?91.

CHEN Bingjie， HUANG Xiaoping， WANG Yan. Wireless sensor network mobile node localization algorithm based on MDS technology and MCL method [J]. Micromachine and application， 2011， 30（6）： 88?91.

[17] 朱海平，于红丞，钟小勇，等.动态无线传感器网络的改进蒙特卡罗定位算法[J].传感技术学报，2012，25（9）：1284?1288.

ZHU Haiping， YU Hongcheng， ZHONG Xiaoyong， et al. Improved Monte Carlo localization algorithm for dynamic wireless sensor networks [J]. Chinese journal of sensors and actuators， 2012， 25（9）： 1284?1288.

[18] 周春月，张洪婷.基于测距权重的蒙特卡罗定位改进算法[J].北京交通大学学报，2016，40（5）：63?69.

ZHOU Chunyue， ZHANG Hongting. Improved algorithm of Monte Carlo positioning based on distance weighting [J]. Journal of Beijing Jiaotong University， 2016， 40（5）： 63?69.

[19] 马晓贤，彭力.一种改进的无线传感器网络DV?Hop定位算法[J].计算机工程与应用，2015，51（21）：97?101.

MA Xiaoxian， PENG Li. An improved DV?Hop localization algorithm for wireless sensor networks [J]. Computer engineering and applications， 2015， 51（21）： 97?101.

[20] 袁鑫，吴晓平，王国英.线性最小二乘法的RSSI定位精确计算方法[J].传感技术学报，2014，27（10）：1412?1417.

YUAN Xin， WU Xiaoping， WANG Guoying. Accurate calculation method of RSSI location for linear least squares method [J]. Chinese journal of sensors and actuators， 2014， 27（10）： 1412?1417.

[21] 张慧敏，柴毅，许磊.无线传感器网络加权质心相对定位算法[J].計算机工程与应用，2010，46（28）：22?24.

ZHANG Huimin， CHAI Yi， XU Lei. Weighted centroid relative location algorithm in wireless sensor networks [J]. Computer engineering and applications， 2010， 46（28）： 22?24.