盾构开挖对桩基内力和变形的影响

方程诚，方诗圣

(合肥工业大学 建筑工程系，安徽 宣城 242000)

0 引言

我国各大城市正在兴建城市轨道交通，城市地铁隧道的挖掘施工工序复杂，而且易造成地表沉降，严重的会造成建筑物变形、开裂。地铁隧道开挖方法目前主要有盾构法、明挖法和浅埋暗挖法等。由于经济的持续发展，交通流量与日俱增，以前的隧道施工方法已不适应工程需求。盾构法安全性高、施工速度快、自动化程度高，不受雨雪天气的影响而且尤其适合在松软含水地层中施工[1]。并且盾构施工不会影响上部地表交通，因此盾构法被越来越多的用于城市地铁的修建。

在我国盾构法施工已经得到了广泛的应用，我国学者对于地铁开挖对周边环境的影响已经做了很多研究，但是这些研究主要集中在盾构开挖对地表沉降变形的影响[2-4]，对上部建筑物的影响研究比较少，对框架结构桩基的研究更少。大部分已有的研究主要采用二维有限元模型和三维有限元模型进行模拟，三维有限元模型考虑了结构与土体的共同的节点位移和相互之间的空间位置关系，因此本文采用三维有限元模型进行研究。[5-12]

本文对某6层框架结构下部桩基础进行系统的受力和变形研究，增进对地下桩基因为盾构沉降而产生内力变形甚至破坏的理解，从而更好的指导实际盾构施工和预防建筑物破坏。

1 建立三维有限元模型

1.1 有限元建模情况

三维有限元模型如图1所示

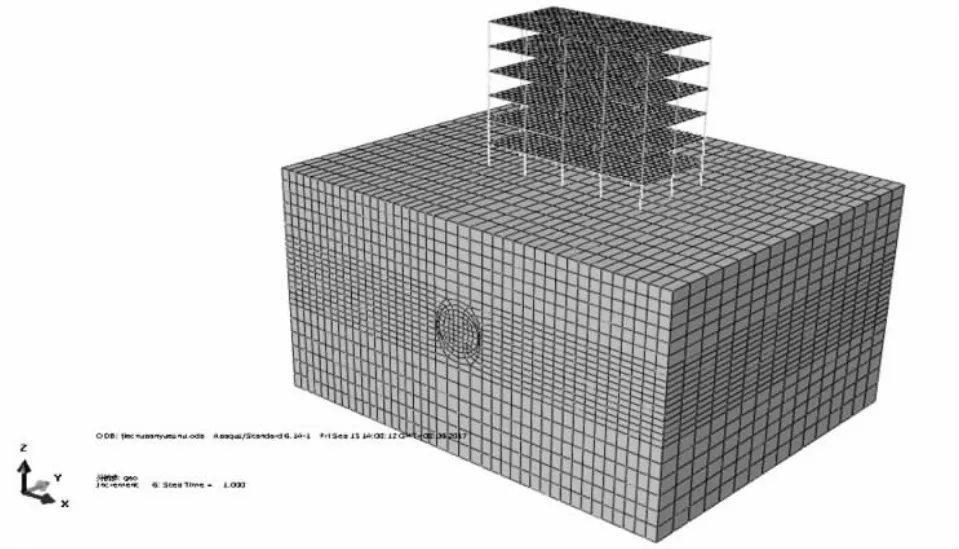
图1 三维有限元模型

模型横剖面和边界约束如图2所示。

模型平面布置如图3所示。

根据盾构开挖有限元模拟中的几个假定[5][10]建立的三维有限元模型的尺寸和边界条件：土体模型的尺寸是长60 m(x方向)、宽48 m(y方向)、边界条件为上表面自由、下表面及土体四周限制垂直方向的位移。建筑物为6层横向三榀框架、桩基础，框架上铺楼屋面板厚0.12 m。桩基础长10 m、桩径0.4 m，柱长3.6 m截面为0.4 5m×0.45 m的矩形截面，梁长6m截面为0.3 m×0.6 m的矩形截面。盾构衬砌外半径3 m厚0.3 m，注浆层外半径3.16 m厚0.16 m，开挖隧洞半径3.16 m，盾构机外壳使用壳单元厚0.2 m。

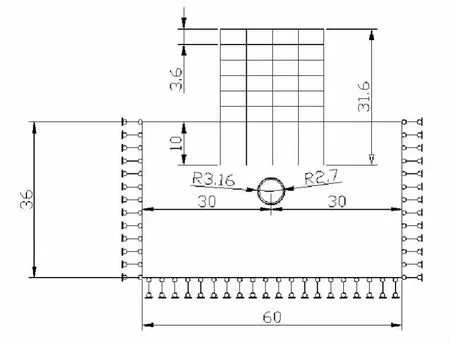
图2 模型横剖面和边界约束 （单位:m）

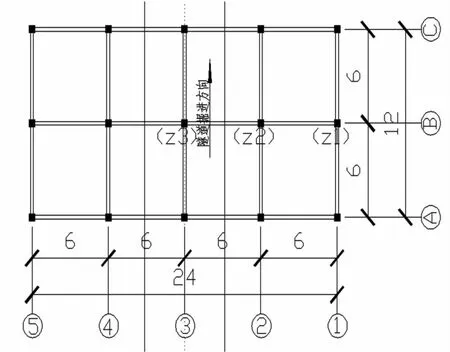
图3 模型平面布置图 （单位:m）

1.2 有限元建模过程如下

（1）框架结构需同时考虑混凝土和钢筋的刚度，如果混凝土采用实体单元、钢筋采用梁单元模拟，则单元数目非常多，不方便建模和计算。因此本文采用等效刚度的方法[12]将钢筋和混凝土的等效刚度计算出来，然后采用梁单元建出整个框架模型，这不仅会给计算带来很大的方便，同时也可保证计算结果一定的准确性。

等效刚度的计算公式为：

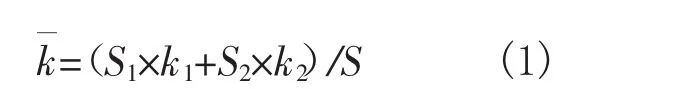
其中，S1为混凝土截面的面积、S2为钢筋截面的面积、S为混凝土和钢筋截面的总面积，k1为混凝土截面的刚度、k2为钢筋截面的刚度。由此计算出钢筋混凝土梁、柱、板的弹性模量为30 GPa，桩的弹性模量为20 GPa。

（2）土体采用摩尔库伦本构模型，由于土体体积太大，所以为土体划分单元时将上部隧道周边土体细分，而将其余土体粗略划分，这样既可以保证计算的精度，又可以加快有限元软件运算速度。

（3）盾构隧道的有限元模拟采用ABAQUS生死单元功能，先将衬砌、注浆层和盾构机外壳杀死，然后将隧道土体按开挖步分步杀死。在杀死土体的同时激活盾构外壳，盾构外壳长9 m、盾构每环距离为3 m。因此盾构开挖三环之后才能重新激活衬砌和注浆层。

（4）盾构机外壳的厚度远小于长度，因此盾构机外壳采用壳单元模拟，土体、衬砌以及注浆层均采用实体单元模拟。

（5）假定受力情况：有限元模型整体受重力、楼屋面板受均布荷载压强为0.25 MPa、盾构掘进面受均布荷载压强为0.3 MPa。

2 有限元计算分析

2.1 盾构过程中桩的变形和受力

盾构会导致不同位置的桩基础产生不同的响应，由于整个有限元模型的位置是对称的。因此选取轴力最大的中间一榀框架下的桩基础作为研究对象，分别为：B1、B2、B3位置处的桩Z1、Z2、Z3，如图3所示。同时将掘进过程分为开挖前、开挖12 m、开挖24 m、开挖48 m四个阶段，以便研究在未开挖、临近、下穿、远离等关键施工节点盾构施工对桩基产生的不同影响。

有限元数值模拟得到在不同开挖距离时Z1、Z2、Z3的桩身水平位移如图4所示。其中从右到左依次为桩Z1、Z2、Z3，Z1与盾构隧道轴线的距离为12 m，Z2与盾构隧道轴线的距离为6 m，Z3与盾构隧道轴线的距离为0 m。

（1）由于隧道开挖会导致桩二次变形，因此开挖前桩就存在水平位移。由图4可知随着盾构掘进桩的水平位移逐渐增大，其中Z1、Z2的桩顶向隧道方向倾斜，桩底向偏离隧道方向倾斜，所以Z1、Z2桩绕桩身某一点逆时针旋转了一定的角度。Z3桩由于在盾构开挖之前已经有一定的水平位移，所以Z3处于隧道正上方时，仍然产生了较小的水平位移。

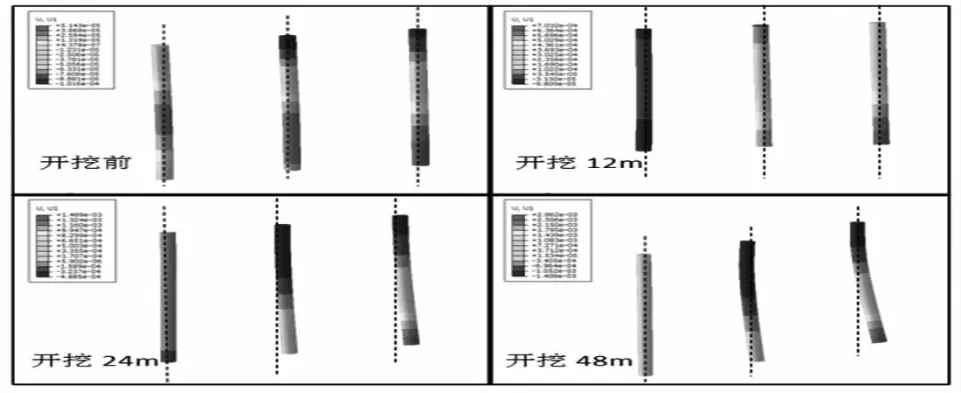
图4 在不同开挖距离时Z1、Z2、Z3桩身水平位移

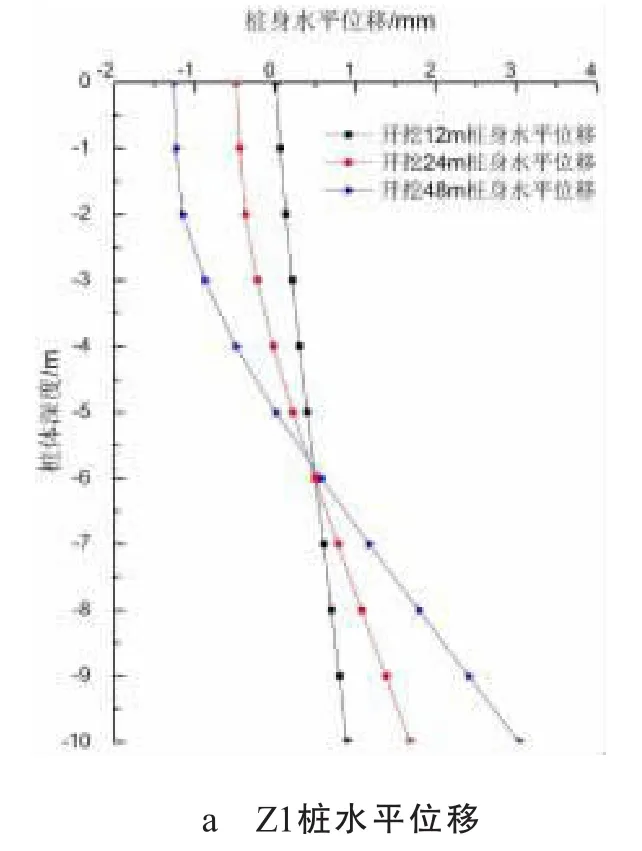
为了进一步研究Z1、Z2桩水平位移变化规律，由有限元分析结果得到Z1、Z2桩水平位移随桩身深度变化的曲线图如图5所示。

图5中水平位移值为正则表示偏离隧道方向，水平位移值为负则表示偏向隧道方向。由图5可知随着盾构的掘进桩顶和桩底的水平位移差逐渐增大，说明桩基础水平位移受盾构影响较大。桩身最大水平位移如表1所示。

表1 桩身最大水平位移mm

最大变化率=max(最大水平位移)/min(最大水平位移)。Z1、Z2、Z3距盾构轴线距离逐渐变小，表1说明桩距盾构轴线的距离对桩底水平位移的影响比桩顶大。

（2）有限元数值模拟得到Z1、Z2、Z3的桩身轴力、弯矩如图6所示。

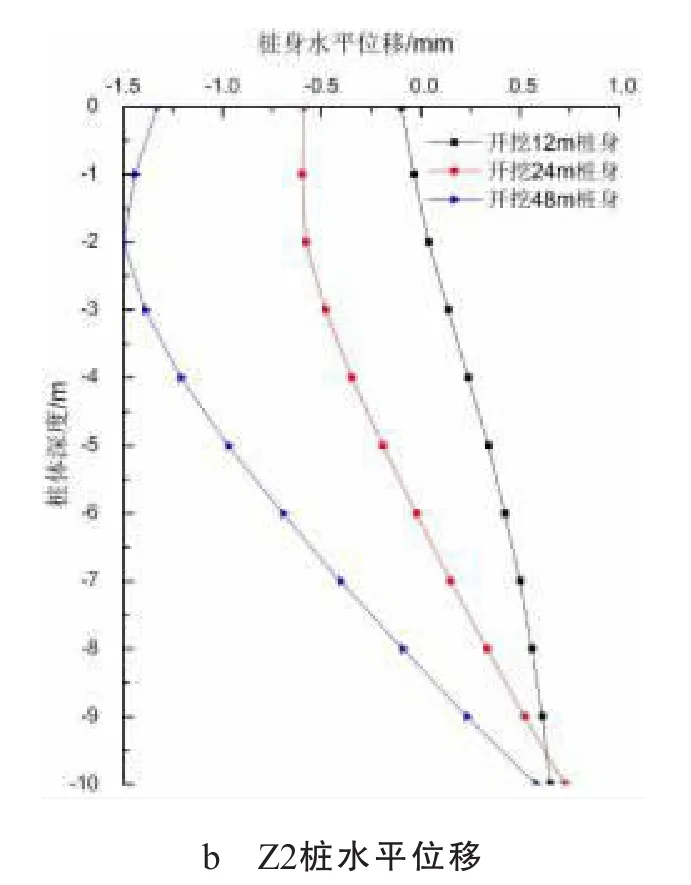
图5 在不同开挖距离时桩水平位移随深度的变化曲线

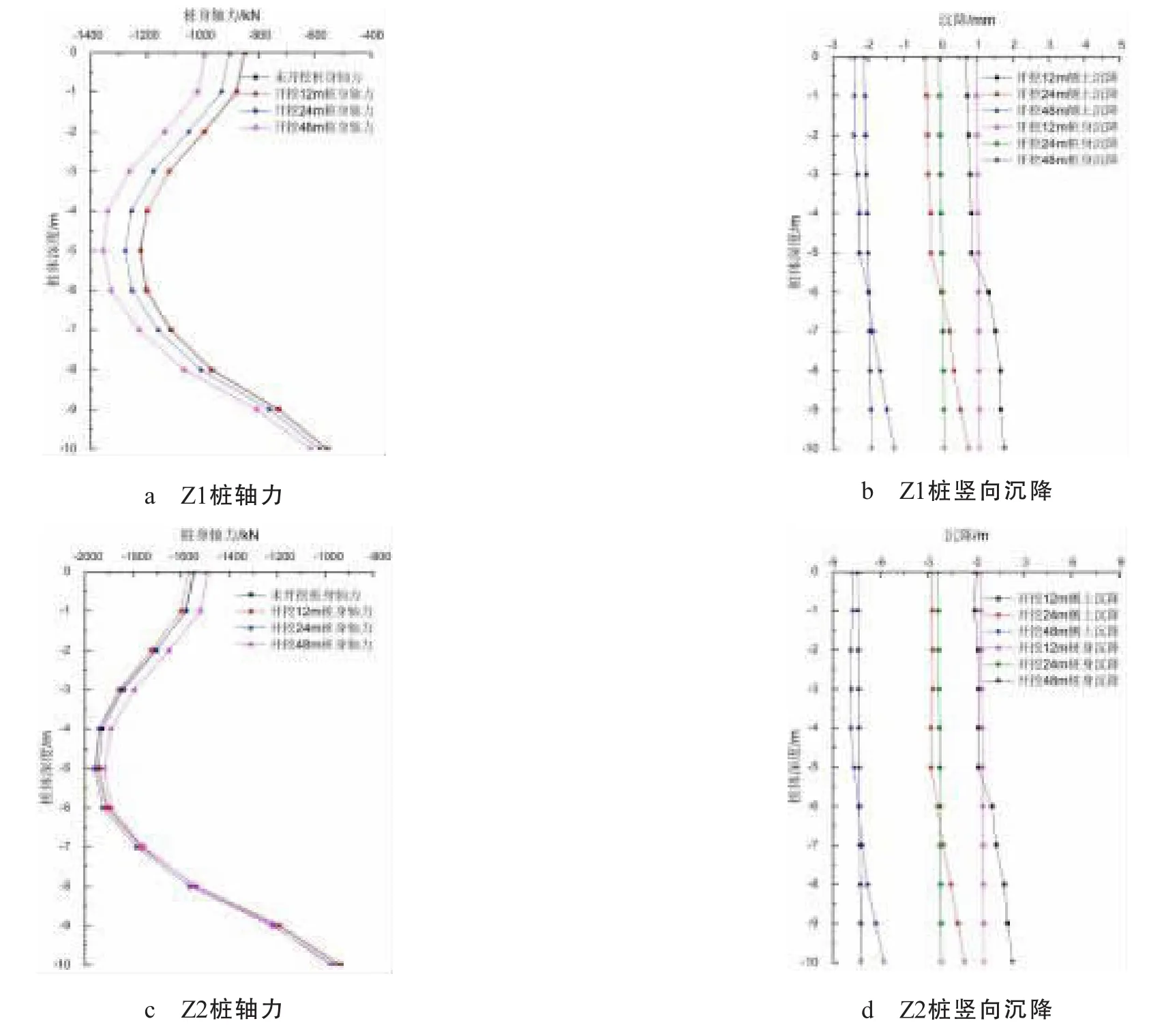
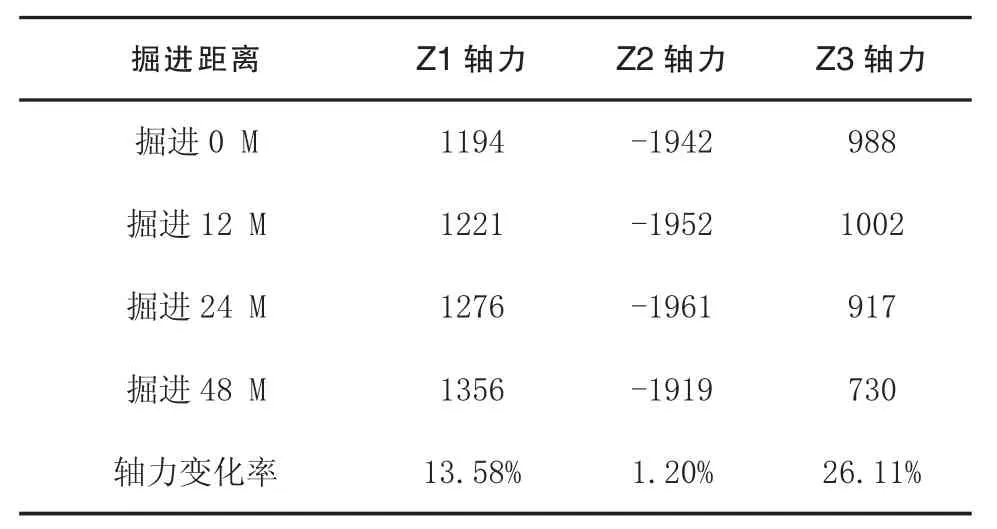
表2 桩身最大轴力kN

由图6a、c、e可知桩的轴力随着距隧道轴线的距离的增大先增大后减小，这说明桩受力并不是距轴线越近越大，桩受力最大值在距隧道一倍隧洞直径附近(Z2附近)。

桩身不同掘进位置处最大轴力如表2所示。

表2说明桩距隧洞轴线距离在两倍隧洞直径附近时桩轴力随着盾构的开挖逐渐增大，桩在隧洞轴线附近时桩轴力随着盾构的开挖逐渐减小。由图6a、c可知，Z1、Z2桩身轴力沿着桩身向下先增大后减小，轴力最大值发生在桩中部，桩轴力增加主要有两个原因：一是隧道开挖会使框架产生附加内力，造成桩轴力增加；二是桩中部以上出现了负摩阻力，造成桩轴力增加。由图6b、d可知，Z1、Z2桩身竖向沉降在桩中部以上时比桩侧土小，在桩中部以下时比桩侧土大。桩中部以上受土体向下的负摩擦力，因此导致桩轴力变大。桩中部以下受土体向上的摩擦力，因此导致桩轴力变小。由图6e可知，Z3桩身轴力沿着桩身向下减小，轴力最大值发生在桩顶部。

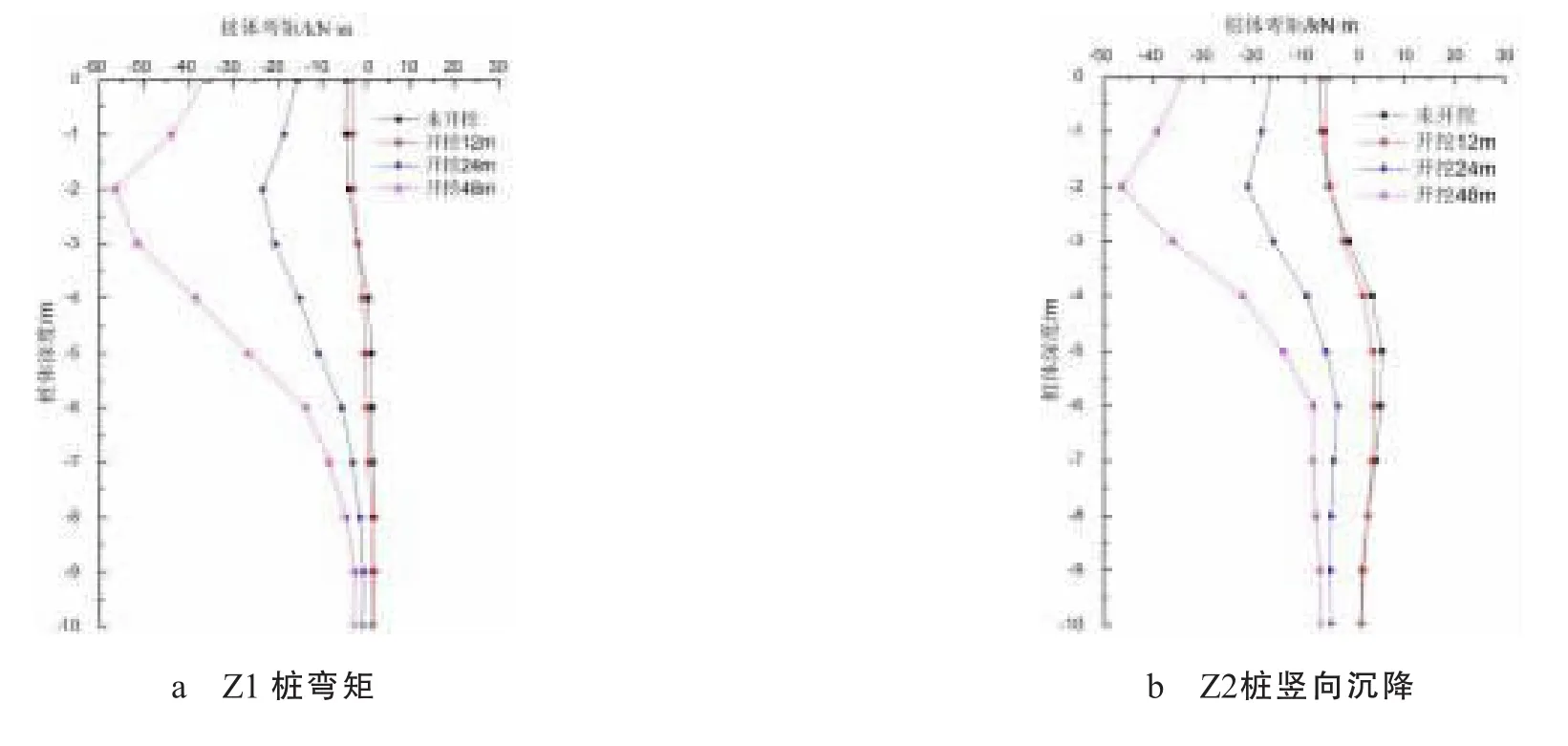
（3）如图7为有限元分析得到的桩身弯矩结果。桩身受拉为正号，桩身受压为负号。不同于其他有关桩身弯矩的研究，本文考虑了上部结构的影响，所以桩顶是有弯矩的。

由图7a、b、c可知，随着开挖的进行隧道轴线两侧Z1、Z2桩的弯矩逐渐增大，Z1弯矩在未开挖时最大为4.68 kN·m，开挖48 m时弯矩最大为56.54 kN·m，增大了1108.12%；Z2弯矩在未开挖时最大为6.61 kN·m，开挖48 m时弯矩最大为46.37 kN·m，增大了601.51%。而隧道中线上方的Z3桩的弯矩不随盾构开挖而变化且近乎为零，这与实际相符表明盾构施工期间隧道中线上方的桩基础不需要考虑弯矩变化，而两侧一定范围内的桩基础离隧道轴线越远越需要考虑盾构开挖对桩身弯矩的影响。由图7a、b可知随着桩深度的增加，Z1、Z2桩的弯矩先增大后减小，这是因为桩土相互作用以及隧道开挖使桩身出现水平位移，进而使桩身弯矩发生了变化。

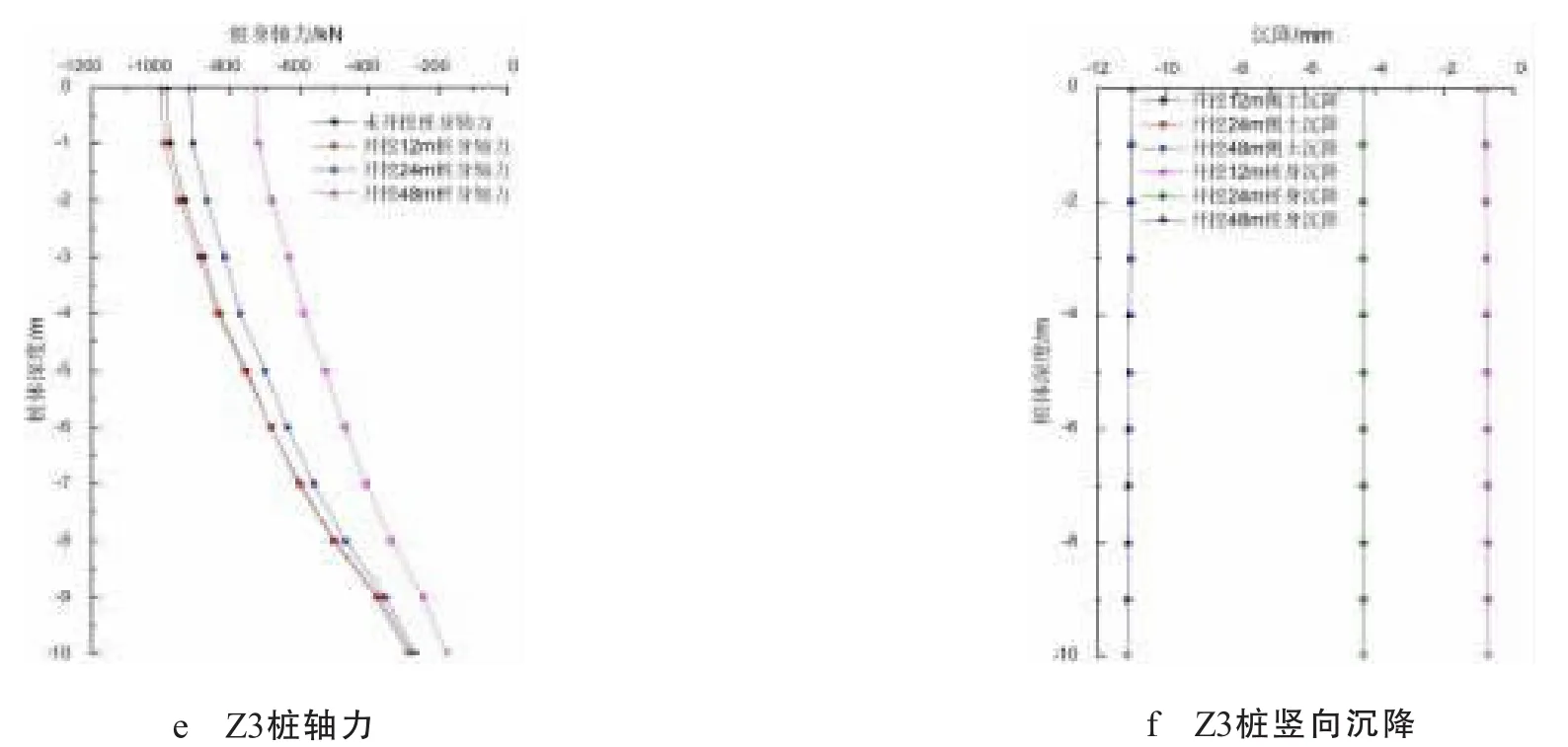
图6 在不同开挖距离时桩竖向位移和轴力随深度的变化曲线

3 结论

本文利用ABAQUS6.14-1，以某框架结构的桩基作为研究对象，在全面考虑模型地表以上框架结构、桩基、地基土体和地铁隧道空间相互作用的基础上建立了结构-土体-隧道模型。该模型上部为典型6层桩基框架结构，本文研究结果对盾构工程中临近建筑物的监控和加固具有普遍的指导意义。

(1)地铁盾构开挖导致隧道轴线两侧桩身桩顶向隧道方向倾斜，桩底向偏离隧道方向倾斜，隧道轴线上方的桩由于在开挖前的桩土相互作用，开挖后也产生了较小的水平位移。桩底水平位移变化率大于桩顶水平位移变化率，因此桩距盾构轴线的距离对桩底水平位移的影响比桩顶大。

(2)地铁盾构开挖在桩身内部引起桩身轴压力变化，桩的轴力随着距隧道轴线的距离的增大先增大后减小，这说明桩轴力并不是距轴线越近越大，桩轴力最大值在距隧道一倍隧洞直径附近。桩距隧洞轴线距离在两倍隧洞直径附近时桩轴力随着盾构的开挖逐渐增大，桩在隧洞轴线附近时桩轴力随着盾构的开挖逐渐减小，所以不同位置的桩受盾构开挖的影响各有不同。由于土体和桩的相对位移造成桩身不同部位产生的摩擦力方向不同，隧洞两侧桩的桩身轴力沿着桩身向下先增大后减小，而隧洞正上方桩桩身轴力沿着桩身向下一直减小。

(3)当盾构开挖面从中间一榀框架桩下方推进到距中间一榀框架桩24 m时，桩的水平位移、弯矩和轴力的变化最为显著，故当开挖面推进到桩轴线并前进4倍洞径以内时，应引起现场施工人员的重视，并采取相应保护措施加固将要通过的桩基础。

(4)隧洞正上方桩桩身弯矩几乎不随桩身深度变化且近乎为零与实际相符，由于桩在土的挤压下产生水平位移使隧洞两侧桩桩身弯矩先增大后减小。桩上部所受弯矩较大且距地面2 m处弯矩最大，所以应采桩基础托换的方法减小该位置处的桩身弯矩。

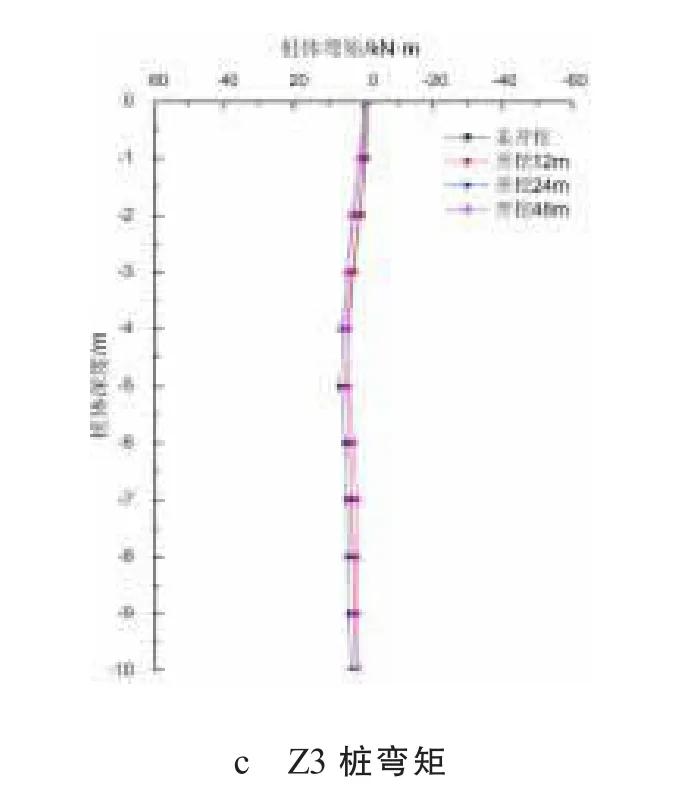
图7 不同开挖距离时桩x方向弯矩随深度的变化曲线