高层框架剪力墙结构的滞回耗能分布
2018-08-06杨少华
王 放,干 洪 ,杨少华
(1.安徽建筑大学 土木工程学院,安徽 合肥 230601;2.安徽工程大学,安徽 芜湖 241000)
关键字:高层框架剪力墙结构;滞回耗能;弱连梁;MPA方法
0 引言
传统的抗震设计规范是在基于承载力的基础上制定的,无法有效判断和控制结构在地震作用下的破坏程度,而基于性能的抗震设计理论是要求结构在不同地震作用下具有相应的抗震性能水准,这种方法要求设计工作者依据建筑的重要性,场地条件等因素,自行制定结构的性能目标并对其进行定性和定量的分析,保证结构在地震作用下的安全性,所以基于性能的抗震设计会成为一种趋势[1]。实现结构基于性能的抗震思想,关键之处就是要有效的控制各个建筑构件在地震作用下的破坏程度,使各个建筑构件在地震作用下达到预期的破坏程度,在能量层面上讲就是要合理分配地震能量在各个构件中的比例。在能量反应分析中,滞回耗能作为最具有工程意义的能量指标具有很大的研究空间,各国学者都对结构在地震作用下的能量分析进行了大量的研究,比如:地震动输入能量谱、滞回耗能谱、阻尼耗能谱等[2-5],结构基于最大变形和耗能能量的损伤模式[6],等等。
大量的震害资料和实验研究表明[7]:结构在地震作用下发生失稳坍塌是由于结构变形和耗能能力不足导致的,因此结构在地震作用下的抗震性能与结构的变形和耗能能力密切相关。本文通过S A P2000建立高层框剪结构模型并对其进行考虑三阶模态组合的MPa方法分析,确定结构的合理耗能分布模式,并用数值分析的方法得出高层框架剪力墙结构合理耗能分布的控制条件。
1 结构地震能量分析
结构在地震作用下产生破坏是由荷载幅值超越破坏和重复加载累积破坏共同作用引起的[8]。Fajfar[4]对结构在强震作用下的地震响应进行了深入研究,结果表明采用承载力、位移等单一的性能指标无法全面反映结构真实的抗震性能,而结构耗能能力则可以全面反映结构抗震能力。能量的输入、转化和耗散过程可以反映结构在地震作用下基本特征,对结构能量反应的研究不但考虑到结构动力特性,而且还考虑到地震作用因素,因此结构耗能能力才是可以综合反映结构抗震能力的指标[9-10]。Fajfar在之前研究的基础上,采用Pushover分析方法制定了框架结构的损伤评估方法,标志着基于能量的抗震设计开始应用于实际工程设计的领域[4]。
在地震动作用下,多自由度体系的运动方程为:

式(1)的两边同时左乘{x˙(t)}T·dt,对地震持续时间t0积分,得到多自由度体系的能量反应方程为[11]:
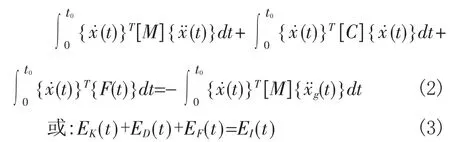
其中,[M]、[C]、{F(t)}分别为多自由度体系的质量矩阵、阻尼矩阵、恢复力向量;{x(t)}、{x(t)}、{x(t)}分别为体系的位移向量、速度向量、加速度向量;x¨g(t)为地震动加速度。

分别为多自由度体系的动能,阻尼耗能,变形耗能,地震动总输入能量。其中EE(t)为体系可恢复的弹性应变能,EH(t)为体系的滞回耗能。
本文重点从结构能量反应的角度,通过研究结构各个构件的累积滞回耗能分布,从能量耗散层面上探究强震作用下框架剪力墙结构实现“强墙肢弱连梁”、形成合理损伤模式的控制条件,为工程设计提供一定的依据。
2 高层框架剪力墙结构层间滞回耗能分布
2.1 模型的建立
本文以现行的抗震设计规范为依据,利用S A P2000建立三个20层的框剪结构模型,平面布置图均如下图1所示,底层层高4.8 m,其余层高均为3.3 m,总高度为67.5 m。抗震设防烈度均为8度,场地类别为二类,地震分组为第一组。各层的均布荷载恒载取5.0,活载取2.0。受力筋选用HRB400级钢筋,分布钢筋选用HRB335,箍筋选用H P B300,采用C35级的混凝土。结构配筋利用P K P M计算。
结构的其余参数如下所示:
(1)模型一:剪力墙厚度取400 mm,框架柱截面为700 mm×700 mm,框架梁截面为 350 mm×800 mm,连梁截面为350 mm×1200 mm,连梁跨度为2500 mm,采用强连梁,跨高比为2.083。

图1 框架剪力墙结构平面布置图
(2)模型二:剪力墙厚度取400 mm,框架柱截面为700 mm×700 mm,框架梁截面为 350 mm×800 mm,连梁截面为350 mm×650 mm,连梁跨度为2500 mm,采用弱连梁,跨高比为3.846。
(3)模型三:剪力墙厚度取350 mm,框架柱截面为800 mm×800 mm,框架梁截面为350 mm×800 mm,连梁截面为350 mm×650 mm,连梁跨度为2500 mm,采用弱连梁,跨高比为3.846。

图2 模型一层间累积滞回耗能分布图

图3 模型二层间累积滞回耗能分布图
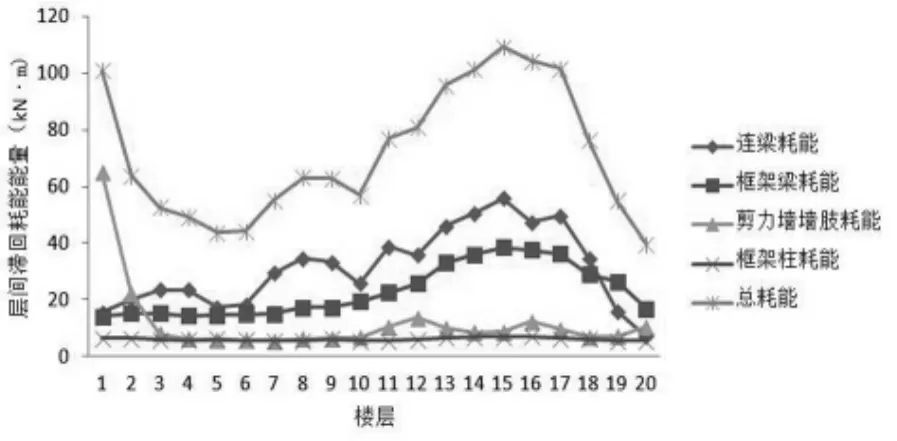
图4 模型三层间累积滞回耗能分布图
2.2 层间滞回耗能分布分析
通过建立三个高层框架剪力墙结构模型,对其进行考虑三阶模态组合的MPa方法分析,得到三个模型的层间累积滞回耗能分布分别如图2、图3和图4所示:
结构在大震作用下的总耗能由连梁、框架梁、剪力墙墙肢和框架柱组成。其中连梁作为抗震设防的第一道防线,在大震作用下允许其破坏,承担了主要的地震动能量,符合基于性能设计的抗震设防要求;框架梁作为连梁之后的第二道防线,其耗能应仅次于连梁,但是从上图可以看出,框架梁的层间滞回耗能要明显小于剪力墙墙肢,显然不符合基于性能设计的抗震设防要求;同时在结构13层附近的剪力墙墙肢处出现了局部耗能集中的现象,并且耗能集中出现的部位会根据地震动选取的不同会发生变化,因此墙肢的耗能分布是随机的、不确定的,显然不符合基于性能设计的抗震设防要求;框架柱作为抗震设防的后备防线,承担的耗能能量很少,框架柱在大震作用下保持弹性,符合基于性能设计的抗震设防要求。因此,设置强连梁的高层框架剪力墙结构的耗能分布是不可控的,不符合基于性能的抗震设防要求。
图3可以看出:连梁、框架梁、剪力墙墙肢和框架柱的耗能分布均符合基于性能设计的抗震设防要求,连梁作为抗震设防的第一道防线,承担了主要的地震动能量,框架梁其次,墙肢底部出现耗能集中,框架柱承担的耗能能量很少,可以忽略不计。
与模型一不同的是:模型二中的剪力墙墙肢也出现耗能集中的现象,但墙肢仅在剪力墙底部两层处出现耗能集中的现象,在墙肢的其他部位则不出现,相比于模型一中局部耗能集中的不确定,模型二中墙肢的集中耗能分布是确定的,在实际工程中便于采取抗震措施对其集中耗能的部位进行加强;同时框架梁的层间滞回耗能要明显大于剪力墙墙肢,符合抗震设防中框架梁作为第二道防线的要求。因此,设置弱连梁的高层框架剪力墙结构耗能分布具有可控性,符合基于性能的抗震设防要求。
模型三同样采用跨高比为3.846的弱连梁模式,相比于模型二,模型三增大了框架剪力墙结构刚度特征值λ(反应总框架和总剪力墙刚度之比的一个参数)。模型三的耗能分布模式与模型二基本保持一致。连梁和框架梁为主要的耗能构件,其中连梁承担了主要的滞回耗能,框架梁其次;剪力墙墙肢只在底部出现滞回耗能集中,在中上部则不会出现;框架柱承担的滞回耗能很少,同样可以忽略不计。模型三与模型二不同之处仅为框架梁相对于连梁的滞回耗能的比例变大。
根据分析可以得出:设置弱连梁的高层框架剪力墙结构模型具有合理的耗能分布模式。
3 高层框架剪力墙结构合理耗能分布的形成条件
3.1 模型的建立
基于上述的研究分析发现:影响高层框架剪力墙结构耗能模式和累积滞回耗能分布的因素在于连梁跨度2a与高度hl,要实现高层框架剪力墙结构在大震作用下合理的耗能模式和耗能分布就需要对连梁的跨度2a与连梁的高度hl进行研究,通过设定连梁的跨度2a与连梁的高度hl的控制条件来引导结构在大震作用下形成合理的耗能模式和耗能分布。
本文建立不同连梁跨度2a与高度hl的高层框架剪力墙结构模型,通过对不同模型层间累积滞回耗能的结果进行分析,来总结出合理的耗能分布模式所对应的连梁跨度2a与高度hl的组合。
本文选取之前的模型二,其它参数保持不变,仅仅改变其连梁跨度2a与高度hl,模型的平面图如图5所示:

图5 框架剪力墙结构模型平面图
连梁跨度2a分别取值为1.5 m、2.5 m、3.5 m、4.5 m、5.5 m,连梁的高度hl分别取值为0.6 m、0.8 m、1.0 m、1.2 m、1.5 m,将其进行组合则得到25个模型,其表示方法如表1所示:

表1 不同连梁跨度和高度组合的框架剪力墙结构模型表示方法
3.2 各模型累积滞回耗能分析结果
本文 给 出 2a2-hl1、2a2-hl2、2a2-hl3、2a2-hl4、2a2-hl5这五个模型的分析结果如图6-图10(该结果为El c e nt r o波、T af t波和L a n z hou波计算结果的算数平均值):
根据上述的耗能分布结果可以看出:2a2-hl1与2a2-hl2的剪力墙只在底部墙肢出现耗能集中的现象,在中上部则保持弹性,因此这两个模型具有合理的耗能分布;而2a2-hl3、2a2-hl4和2a2-hl5在墙肢的中上部则出现耗能集中的现象,因此这三个模型则不具备合理的耗能分布。

图6 模型2a2-hl1层间累积滞回耗能分布图
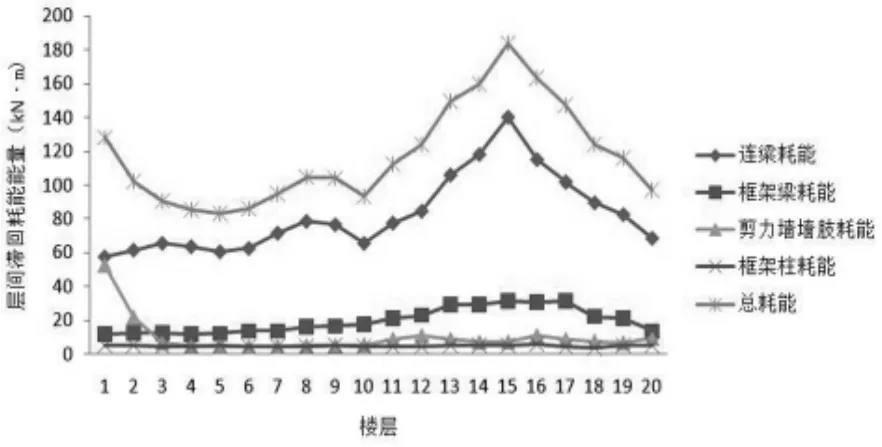
图7 2a2-hl2模型层间累积滞回耗能分布图

图8 2a2-hl3模型层间累积滞回耗能分布图

图9 2a2-hl4模型层间累积滞回耗能分布图

图10 2a2-hl5模型层间累积滞回耗能分布图

表2 合理耗能分布模式下的连梁跨度与高度组合
同时,对其余的各组连梁的跨度2a与高度hl的组合,得到具有合理的耗能分布的组合如表2所示:
3.3 高层框架剪力墙结构合理耗能分布的形成条件
通过对25组连梁不同跨度2a与高度hl组合的高层框架剪力墙结构耗能分布模式进行研究,得出四组合理耗能分布模式下所对应的跨度2a与高度 hl组合,分别为 2a2-hl2、2a2-hl3、2a2-hl4、2a2-hl5,根据这四组数据可以采用数值分析的方法得到跨度2a与高度hl的函数关系,如图11所示:

图11 合理耗能分布模式下连梁跨度与高度的函数关系图
因此,只要满足2a≥-2.043[hf]2+9.026[hf]-3.431便可以实现“强墙肢弱连梁”的结构模式,从而形成合理的滞回耗能形式。在实际工程设计中,可以采用这一数值关系来使结构在大震作用下具有合理的耗能机制与破坏模式。
4 结论
本文以S A P2000软件为基础,结合高层框架剪力墙结构详细介绍了高层框架剪力墙结构在大震作用下的层间滞回耗能分布及其合理耗能分布的控制条件。得出的结论为:
(1)对高层框剪结构模型进行考虑三阶模态组合的MPa方法分析,得出层间累积滞回耗能分布结果,表明设置弱连梁的结构模型具有合理的耗能分布模式;
(2)根据合理耗能分布模式的分析,可以得知连梁的跨度2a与高度hl是影响框架剪力墙结构合理耗能分布的重要因素;
(3)对不同连梁的跨度2a与高度hl进行不同组合的分析,采用数值分析方法得出框剪结构合理耗能分布的控制条件,即当满足2a≥-2.043[hf]2+9.026[hf]-3.431这个条件时,便可以实现“强墙肢弱连梁”的结构模式,从而形成合理的滞回耗能形式。在实际工程设计中,可以采用这一数值关系来使结构在大震作用下具有合理的耗能机制与破坏模式。
