语言值直觉模糊概念格及其应用

邹 丽 冯凯华 刘 新

1(辽宁师范大学计算机与信息技术学院 辽宁大连 116081)2 (辽宁师范大学数学学院 辽宁大连 116029) (zoulicn@163.com)

概念格于1982年由德国数学家Wille提出[1]，也叫做形式概念分析(formal concept analysis, FCA).它是一种表达概念和概念层次关系的数学理论，是进行数据分析和知识处理的数学工具.概念格理论中有2个基本元素，分别是形式背景和形式概念，其中形式背景是概念格的数据表现方式，由对象集、属性集以及两者上的一个关系构成.基于形式背景，通过一对派生算子可以构造形式概念[2]，即构造概念的外延和内涵.目前概念格已广泛应用于众多领域[3-8].Yao等人[9-10]研究了粗糙集理论框架下的概念格理论.张文修、王国胤等人[11-13]进一步研究了粗糙集与信息系统的属性约简和规则提取问题.李金海等人[14-15]从概念外延的角度研究了合理刻画属性重要性的指标，给出了概念格属性约简的判定定理，并以这些指标作为启发式信息设计了一种概念格启发式属性约简算法.

在确定的形式背景中，形式概念及其概念格都是精确的，但是现实应用中，大多数对象与属性的关系都是模糊的，研究学者使用隶属度来表示对象与属性的模糊关系，提出了模糊形式概念分析，模糊概念格[16]已成为新的研究领域.Burusco等人[17]首先提出了使用三角模对传统的伽罗瓦联系进行模糊扩展的方法.Bělohlvek等人[18-20]基于剩余格理论在模糊形式背景下提出了模糊概念的定义，并证明所提出的概念几乎满足所有经典形式背景下概念的性质.Krupka等人[21]把形式概念分析引入到模糊集上，将形式背景中的值由最初的0或1的二元数据，扩充为可以是[0,1]区间的任意数值.Krupka通过把不完备的不确定信息转化为不完备的模糊形式背景，提出了在不完备模糊形式背景下的建格算法.

直觉模糊集从隶属和不隶属2个方面刻画人们认知过程中的模糊性，为处理模糊性问题提供了更丰富的信息.通过直觉模糊集刻画对象与属性的直觉模糊关系，进一步进行直觉模糊概念分析具有重要的理论意义和实际应用价值.朱宪杰等人[22]利用直觉模糊逻辑算子构造了直觉模糊概念格，通过直觉模糊集的水平截集定义了可辨识属性矩阵，给出了直觉模糊概念格的一种属性约简方法；马明华等人[23]研究了直觉模糊信息系统的约简问题，从正关系和负关系两方面考虑了对象与属性间的直觉模糊信息，并根据直觉模糊关系中的正负信息将属性值进行排序，得到了对象集和属性集之间的支配关系，构造了新的概念格模型，并提出了概念格的属性约简方法；李磊军等人[24]在三支决策视角下进行了直觉模糊形式背景和模糊形式背景中概念格之间的分析与比较，探究了它们之间的内在联系，分析了直觉模糊形式背景中的概念格具有数据存储所占空间更小、属性约简更简洁的优势.

实际中大量的问题常常无法用精确的数值表示，模糊语言值在这些问题的表示中具有简单、易于理解等优势，例如在中医疾病诊断过程中，主要通过望闻问切来进行诊断，而病人也是用“有点疼”、“很严重”等自然语言来进行症状的描述.模糊语言值信息处理是目前智能信息处理的热点研究方向，徐泽水等人[25]提出了虚拟语言术语的语法和语义，将该语言决策方法应用于语言信息融合等应用中；邹丽等人[26-27]建立了2n元语言真值直觉模糊代数，并基于语言真值格蕴涵代数建立了语言真值直觉模糊格，从正反两方面处理语言值模糊信息，且可同时处理语言值信息的可比性和不可比性，并分析其不可约元的蕴涵性质；裴峥等人[28]提出了加权不平衡的语言聚合算子，通过综合评价语言信息的价值、信念程度和专家权重，该算子可以处理不完整或不确定的语言信息，可用于解决不平衡的语言多属性群决策问题.徐扬等人[29-32]提出了语言真值格蕴涵代数及语言真值格值命题逻辑系统.在语言真值格蕴涵代数中，对语气算子的继承性进行修正，使得语言值之间序的关系更贴近自然语言的语义.语言值处理方面的研究对控制理论、模式识别、决策理论、机器学习等领域具有非常重要的意义[29].

在上述工作的基础上，本文将语言值直觉模糊对与直觉模糊形式背景结合，定义了语言值直觉模糊形式背景，构造语言值直觉模糊概念格，研究了语言值直觉模糊概念之间以及语言值直觉模糊概念格之间的贴近度，并提出了语言值直觉模糊概念格的模式识别方法，将其应用于中医疾病诊断识别中，说明此方法的有效性.

1 预备知识

定义1[29]. 语言真值直觉模糊格.基于2n元语言真值格蕴涵代数建立语言真值直觉模糊格LV2n=(LV2n,∪,∩).其中，((hn,t),(hn,f))和((h1,t),(h1,f))分别为LV2n的最大元和最小元；t表示为真，即肯定的评价；f表示为假，即否定的评价.如图1所示，对任意((hi,t),(hj,f))，((hk,t),(hl,f))∈LV2n，((hi,t),(hj,f))≤((hk,t),(hl,f))当且仅当i≤k,j≤l，且

1) ((hi,t),(hj,f))′=((hn-j+1,t),(hn-i+1,f));

2) ((hi,t),(hj,f))→((hk,t),(hl,f))=((hmin(n,n-i+k,n-j+l),t),(hmin(n,n-i+l),f));

3) ((hi,t),(hj,f))∪((hk,t),(hl,f))=((hmax(i,k),t),(hmax(j,l),f));

4) ((hi,t),(hj,f))∩((hk,t),(hl,f))=((hmin(i,k),t),(hmin(j,l),f)).

Fig. 1 Hasse diagram of linguistic truth-valued intuitionistic fuzzy lattice LV2n图1 语言真值直觉模糊格LV2n的哈斯图

定理1[29]. 对任意(hi,t)(hj,f)∈LV2n，(i,j=1,2,…,n,i≤j)，((hi,t),(hj,f))是一个语言真值直觉模糊对当且仅当i≤j.

令语气词集H={hi|i=1,2,…,n}，语气词hi则表示“略，一般，很，…”等描述程度的语气词，评价词集为{t,f}.

Fig. 2 Hasse diagram of 10-element linguistic truth- valued intuitionistic fuzzy lattice LV10图2 十元语言真值直觉模糊格LV10的哈斯图

本文以十元语言真值格蕴涵代数为前提，即语气词集H={hi|i=1,2,3,4,5}，其中语气词h1表示“略”，h2表示“有点”，h3表示“一般”，h4表示“很”，h5表示“绝对”，评价词集为{t,f}，则基于十元语言真值格蕴涵代数的语言真值直觉模糊格LV10如图2所示:

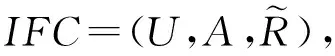
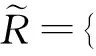
XΔ={|a∈A},
∀b∈B},

规定∅Δ={a,1,0},另外，如果b∉B，则

2 语言值直觉模糊概念格

本节给出语言值直觉模糊形式背景的定义及其形式概念分析.

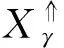
Table 1 Linguistic-Valued Intuitionistic Fuzzy Formal Context表1 语言值直觉模糊形式背景

基于定义5,6和文献[16-21]中的方法，容易证明语言值直觉模糊概念的定理2成立.

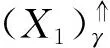
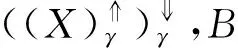
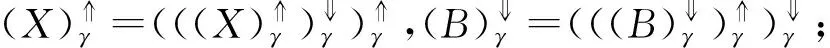
根据定理2，我们有推论1.

基于定理2和定义7，可以得到定理3.

例2. 在例1中，基于图2、定义7和表1，({1,2,3},{a,c})和({3},{a,b,c})是γ=((h4,c1),(h4,c2))水平下的语言值直觉模糊概念，({({1,2,3},{a,c}),({3},{a,b,c})},∨,∧)是一个完备格.

3 语言值直觉模糊形式概念之间的贴近度

本节给出语言值直觉模糊概念及其语言值直觉模糊概念格之间的贴近度公式.直观地，语言值直觉模糊概念格刻画了语言值直觉模糊形式背景中概念的层次关系，若语言值直觉模糊概念理解为对象集和属性集之间的一种知识表达，则本节提出的贴近度用来刻画给定知识与已有知识之间的相似性并用于决策分析中.

1) 语言值直觉模糊概念之间的贴近度

(1)

其中，w1和w2为权重，即w1,w2∈[0,1]且w1+w2=1;|·|表示集合的势，即集合中的元素个数.

直观地，γ水平下2个语言值直觉模糊概念之间的贴近度D((X1,B1),(X2,B2))通过其外延和内涵之间的相似性刻画，其中权重体现了外延和内涵在贴近度中的重要性，D((X1,B1),(X2,B2))越大，表示(X1,B1)与(X2,B2)越相似.

性质1. 对LVIFLγ中的任意2个语言值直觉模糊概念(X1,B1)和(X2,B2)，

① 0≤D((X1,B1),(X2,B2))≤1；

②D((X1,B1),(X2,B2))=D((X2,B2),(X1,B1))；

③D((X1,B1),(X1,B1))=1.

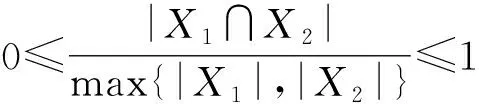
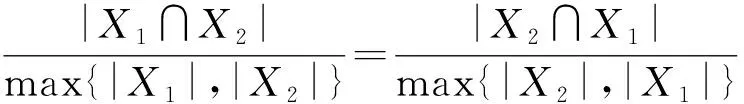
证毕.

2) 语言值直觉模糊概念与语言值直觉模糊概念格之间的贴近度

(2)

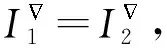
证毕.

3) 语言值直觉模糊概念格之间的贴近度

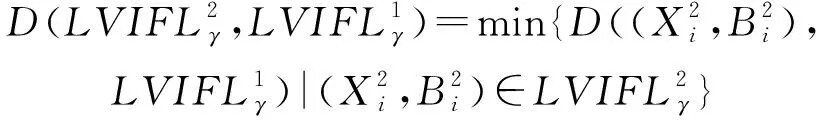
(3)

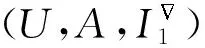
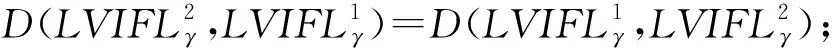
证明. 根据性质1和2，性质3显然成立.

证毕.

基于语言值直觉模糊概念及其语言值直觉模糊概念格之间的贴近度，多个语言值直觉模糊形式背景下的模式识别按以下步骤完成：

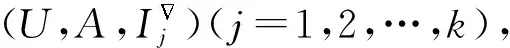
Step4. 将各γ水平下语言值直觉模糊概念格的贴近度求和，即∀j∈{1,2,…,k}，

(4)

D(LVIFL0,LVIFLj)=max{D(LVIFL0,
LVIFLj′)|j′=1,2,…,k}.

(5)

4 实 例

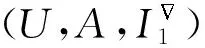
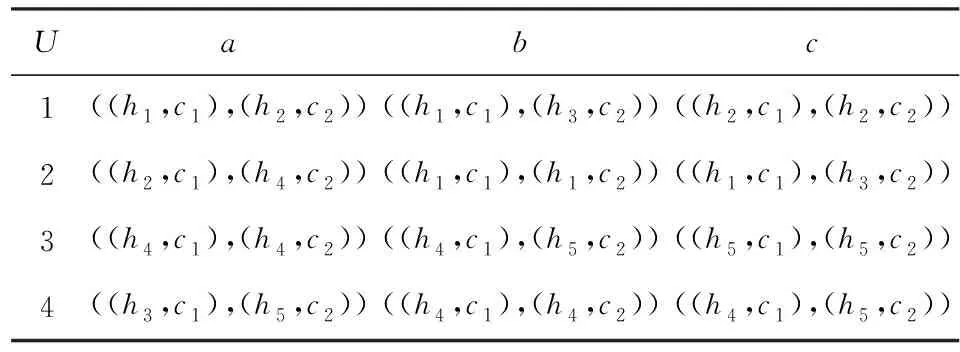
Table 2 Linguistic-Valued Intuitionistic Fuzzy FormalContext of the Common Cold

Table 3 Linguistic-Valued Intuitionistic Fuzzy FormalContext of the Viral Pharyngitis

Table 4 Linguistic-Valued Intuitionistic Fuzzy FormalContext of the Pneumonia

Table 5 Linguistic-Valued Intuitionistic Fuzzy FormalContext of the Symptoms of a Patient

根据表2～5的形式背景描述，语言值直觉模糊形式背景下的模式识别步骤为：

Step1. 普通感冒、病毒性咽炎与肺炎的各γ水平下语言值直觉模糊形式概念见表6～8.

Step2. 按定义7，病人症状的各γ水平下语言值直觉模糊形式概念见表9.

Table6γLevelLinguistic-ValuedIntuitionisticFuzzyFormalConceptLatticeoftheCommonCold

表6 普通感冒的γ水平下的语言值直觉模糊概念格

Table7γLevelLinguistic-ValuedIntuitionisticFuzzyFormalConceptLatticeoftheViralPharyngitis

表7 病毒性咽炎的γ水平下的语言值直觉模糊概念格

Table8γLevelLinguistic-ValuedIntuitionisticFuzzyFormalConceptLatticeofthePneumonia

表8 肺炎的γ水平下的语言值直觉模糊概念格

Table9γLevelLinguistic-ValuedIntuitionisticFuzzyFormalConceptlatticeoftheSymptomsofaPatient

表9 病人症状的γ水平下的语言值直觉模糊概念格

表与和的贴近度

Step4. 基于表10，利用式(4)，可得到D(LVIFL0,LVIFL1)，D(LVIFL0,LVIFL2)和D(LVIFL0,LVIFL3)，见表11.基于表11和式(5)，可得到和病人症状贴近度最高的是肺炎，即根据病人症状，其为肺炎的可能性最大，其次是病毒性咽炎，是普通感冒的可能性最小.

Table 11 Degree of Similarity Between LVIFL0 andLVIFL1,LVIFL2 or LVIFL3

本文方法与文献[33]的区别是:文献[33]使用模糊形式背景描述了一个诊断病例，通过构建模糊形式概念格，给出了智能诊断方法.由于未使用语言值刻画各种症状，导致文献[33]的属性集合较大，增加了生成模糊形式概念格的难度.本文运用语言值在中医疾病诊断领域进行智能诊断，属性集规模较小且能够更好地表达病人对病情的描述，减少数据损失，从而得到更智能的诊断结果.

5 结 论

语言值直觉模糊概念格相对于直觉模糊概念格，减少了将语言转换为数值计算的过程，从根本上减少了处理数据的误差，用非常贴近自然语言的语言值对各个对象的属性进行描述，不仅可以使问题描述更贴近人类语言，而且可以从正反两方面描述模糊信息.本文利用语言值直觉模糊集，定义了语言值直觉模糊形式背景，给出了基于语言值直觉模糊集的形式概念定义，并利用语言值直觉模糊格生成了语言值直觉模糊概念格，通过语言值直觉模糊概念及其语言值直觉模糊概念格之间的贴近度，给出了基于语言值直觉模糊概念格的模式识别方法，该方法计算病人症状语言值直觉模糊概念格与可能患得疾病语言值直觉模糊概念格之间的贴近度，从而诊断最有可能患得疾病类型.该方法更有效地处理由人类自然语言描述的决策分析问题，符合人类的思考方式，为中医疾病领域提供智能化诊断方法.

在语言值直觉模糊概念格的研究中，对于不可比的语言值直觉模糊对需进行更深的研究.中医智能诊断领域疾病的自动诊断识别还需要进一步研究，我们将更深层次地研究每一种疾病的症状权重计算，对中医诊断专家系统进行完善，使语言值直觉模糊概念格在中医疾病智能诊断方面更好地发展.

ZouLi, born in 1971. PhD, professor, master supervisor. Her main research interests include multi-valued logic, uncertain reasoning and intelligent information processing, etc.

FengKaihua, born in 1993. Master candidate. Her main research interests include multi-valued logic, uncertain reasoning and intelligent information processing, etc.

LiuXin, born in 1967. Associate professor. His current research interests include intelligent information processing, decision making.