提高非量测相机高程精度关键技术分析

庄利有，方德涛，刘珊珊,徐 婵

(辽宁省摄影测量与遥感院，辽宁 沈阳 110034)

随着近年来轻小型无人机技术的不断成熟，无人机航空摄影测量技术的逐步完善，无人机航摄已经成为新兴低空遥感影像获取的重要手段，并具有良好的发展前景[1-4]。

但相对于载人机航摄系统来说，无人机航摄遥感系统由于飞行平台与任务载荷自身特点，依然有以下几个方面的问题。首先，无人机飞行平台飞行姿态不稳定。无人机体积小、质量轻，在空中作业时极易受到气流干扰，飞机姿态在俯仰方向和横滚方向上频繁变化，使曝光像片倾角超限，从而造成立体模型扭曲，高程误差变大甚至超限。其次，无人机载荷小，只能搭载非量测数码相机，这种相机有较大的镜头畸变，最大可达20～40像素。畸变会使物点、投影中心、像点三点不共线，同名光线不再相交，空间后方交会精度降低，重建物体的几何模型变形。然后，无人机也无法搭载高精度曝光同步设备及GNSS/IMU系统，以致摄站位置精度存在较大误差，影响平面与高程精度。最后，由于无人机航摄使用普通数码相机的像幅小得多，这样会造成摄影基线变短，基高比变小，从而使空中三角形不稳定，降低了解算的稳定性[5-8]。

针对以上问题，本文结合某丘陵地区无人机航摄数据，通过设计多种试验方案，验证基于非量测数码相机的几种技术与方法对高程精度的影响。试验结果表明，相机标定、差分GPS和飞行构架航线等可以有效提高无人机航摄的高程精度，为今后生产提供有价值的参考。

1 原 理

1.1 相机检校原理

从几何上理解，数码相机是一个四棱锥体，其顶点是相机物镜的中心，其底面就是相机的成像平面(即影像)。由于在加工、安装的过程中，相机的物镜存在一定的误差，使得物方平面上直线的影像不是直线，这种误差称为物镜的畸变差。镜头畸变分为径向变形、偏心变形和切向变形。径向变形主要由透镜的径向曲率误差造成像主点的径向偏移，离中心越远，变形越大；偏心变形和切向变形源于装配误差，分别由相机光学组件轴心无法共线和CCD面阵排列误差造成[9]。3种变形共同导致了数字影像的畸变，其数学模型表示为

(1)

式中，(x，y)为像点坐标；(x0，y0)为像主点坐标；r为像点向径；K1，K2，K3，P1，P2为畸变参数。用于测量的数码影像，为了达到必要的测量精度，必须对相机进行检校，以得到其畸变差参数，并对数码影像进行畸变差纠正。

1.2 GPS辅助空三原理

GPS辅助空中三角测量是利用机载GPS和基站数据，采用载波相位技术进行事后差分处理，获取高精度的曝光时刻摄站中心坐标，并将其作为带权非摄影测量观测值参与联合平差，以达到减少野外控制点的目的[10]。

设以M为原点的地面坐标系中，GPS天线相位中心A和摄影中心S的坐标分别为(XA,YA,ZA)和(XS,YS,ZS)，通过像片姿态角φ、ω、κ得到顾及动态GPS系统误差的变换关系

(2)

式中，R为像片姿态角表示的正交变换矩阵；(u,v,w)为GPS相位中心A在像片坐标系中的坐标；(aX,aY,aZ)和(bX,bY,bZ)分别为GPS线性偏移系统误差参数中固定部分和随时间变化部分；t为曝光时刻；t0为参考时刻。将式(2)按泰勒级数展开至一次项并与光束法平差误差方程联立，构成GPS辅助光束法区域网平差的基础方程。选取适当的权函数形式后，则可用最小二乘法求解物方坐标最或是值，获得精确的外方位元素[11]。

1.3 构架航线区域网平差原理

构架航线又叫控制航线，是指在航摄区内飞行的若干条与常规航线近似垂直且航高不等的航线。对于一条构架航线与相邻两条常规航线之间的连接点，可设常规航线用i标号，构架航线用j标号，在原始误差方程基础上两两相减，消去待定坐标得到等效误差方程

(3)

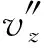
2 试 验

2.1 试验数据获取

本试验采用CW-10无人机平台搭载SONYa7R非量测相机获取低空遥感影像。在航飞前，借助于室内检校场对相机进行标定[13]，获得相机检校参数见表1。

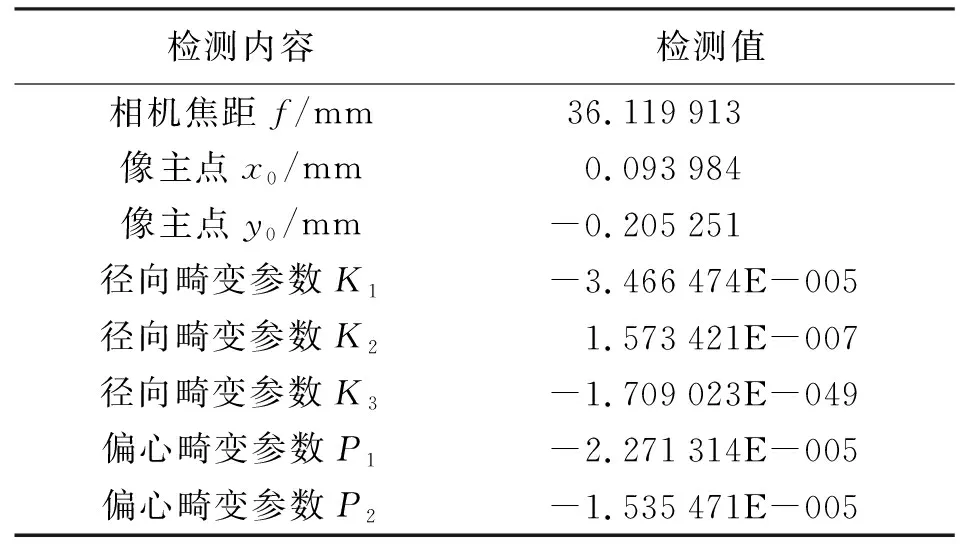
表1 相机检校参数

本试验选取辽宁省喀左县内一处低山丘陵区作为研究区域，并将区域划分成3个试验区，分别是矩形的测区Ⅰ和条带形状的测区Ⅱ和测区Ⅲ。测区Ⅰ飞行常规航线11条，构架航线2条，获取影像548张。测区Ⅱ和测区Ⅲ均飞行常规航线5条，构架航线5条，获取影像分别为413张和432张。3个试验区主要航摄飞行参数见表2。

3个试验区像控点采用飞前布控与飞后布控相结合的方式，为了检验空三区域网平差的高程精度，在3个试验区分别选取一定数量的检查点。像控点与检查点均利用辽宁CORS系统进行野外实地测量。

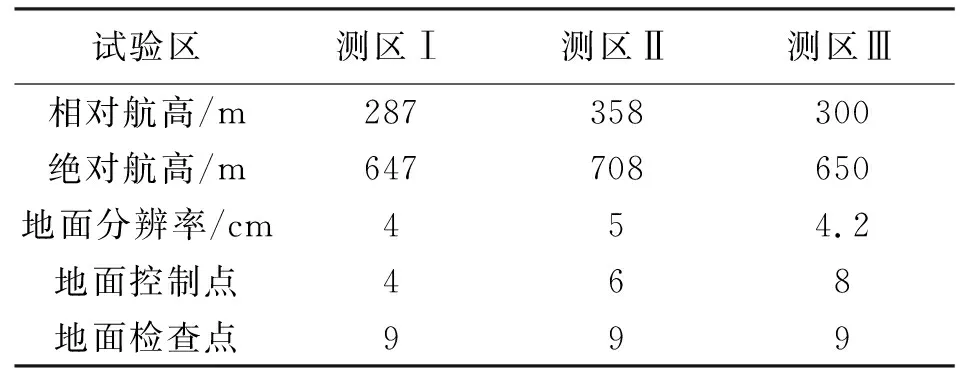
表2 试验主要技术参数

2.2 试验方案

本文设计了3组试验：试验1是为了验证非量测相机标定对高程精度的影响；试验2是为了验证差分GPS对高程精度的影响；试验3是为了验证构架航线对高程精度的影响。其中试验1对3种试验方案进行了对比；试验2和试验3分别对2种方案进行了对比，具体试验方案见表3。试验1方案的控制点和检查点分布如图1所示。试验2、3方案的控制点和检查点分布如图2所示。

表3 试验方案设计

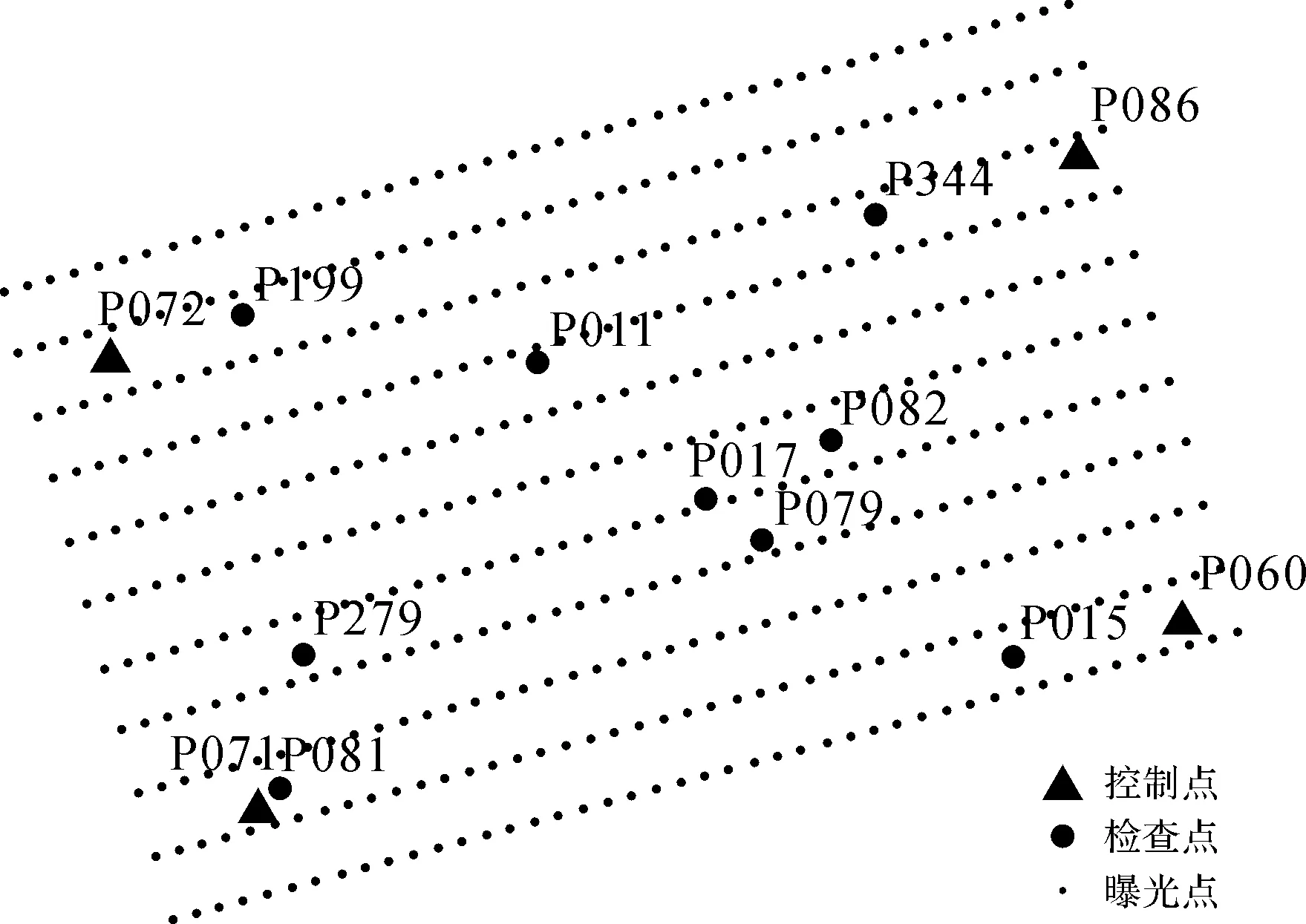
图1 试验1控制点与检查点分布

2.3 试验结果分析

试验1选用了四角四控制点方案，GPS参与区域网平差计算，且加入了GPS安装偏移与坐标系偏移2个改正量，但没有加入构架航线，这样能剔除构架航线对高程影响因素，更好地反映相机检校对高程精度的影响。试验1的3种方案各检查点高程误差绝对值统计如图3所示。

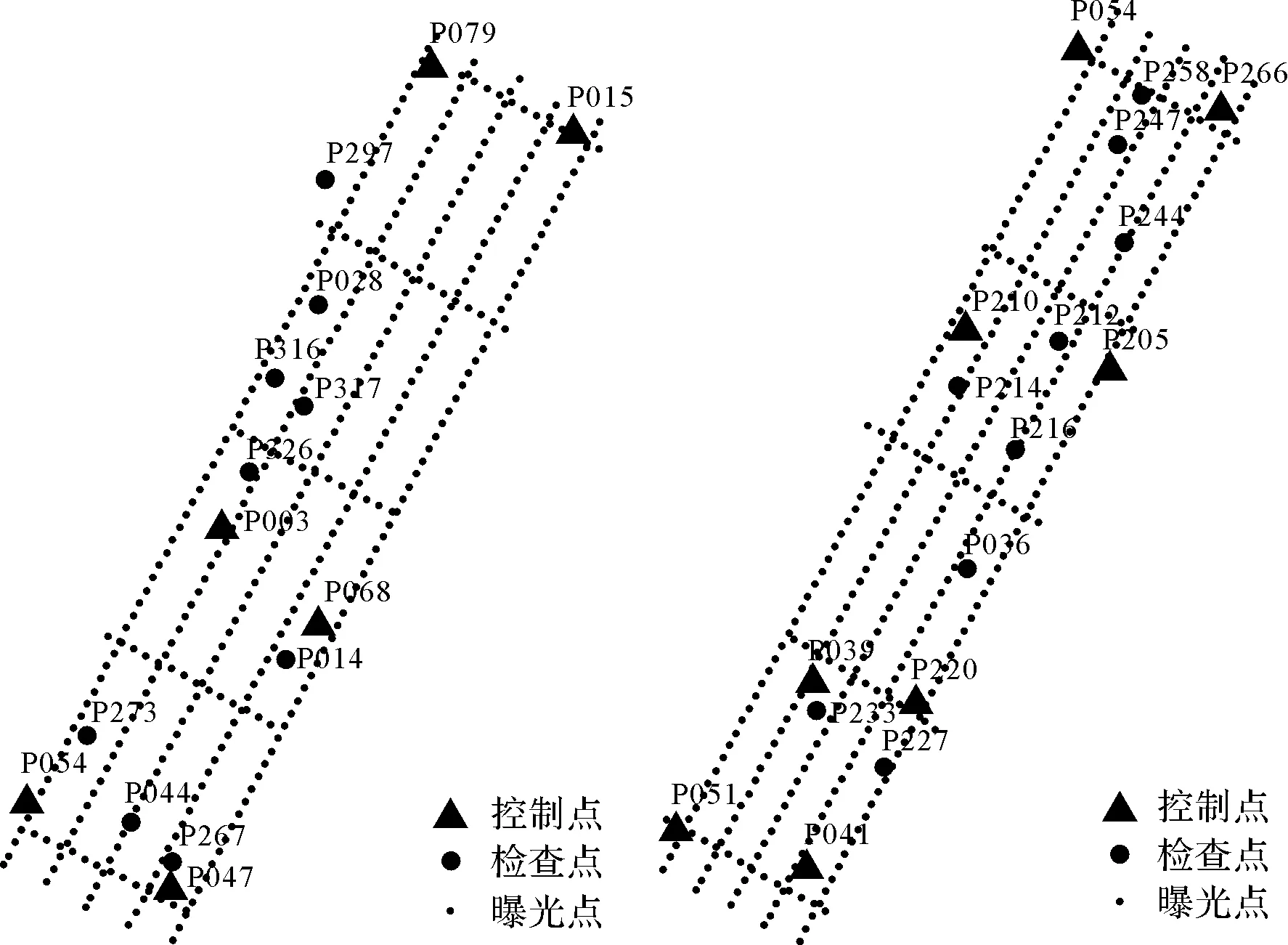
图2 试验2、3控制点与检查点分布

方案1采用原始无人机航摄原始像片，其检查点平面中误差为0.295 m，高程中误差为0.628 m；方案2采用纠正过畸变差像片，其检查点平面中误差为0.226 m，高程中误差为0.302 m；方案3采用原始航摄像片，在区域网平差过程中进行相机自检校，其检查点平面中误差为0.223 m，高程中误差为0.332 m。

图3 试验1检查点高程误差统计

试验2测区是条带形状区域，选用四角加中间六控制点方案，5条航摄航线和5条构架航线，GPS参与区域网平差计算，用相机自检校功能进行畸变差纠正，只是方案4采用原始POS数据，方案5采用后差分POS数据作为摄站坐标。试验2的2种方案各检查点高程误差绝对值统计如图4所示。

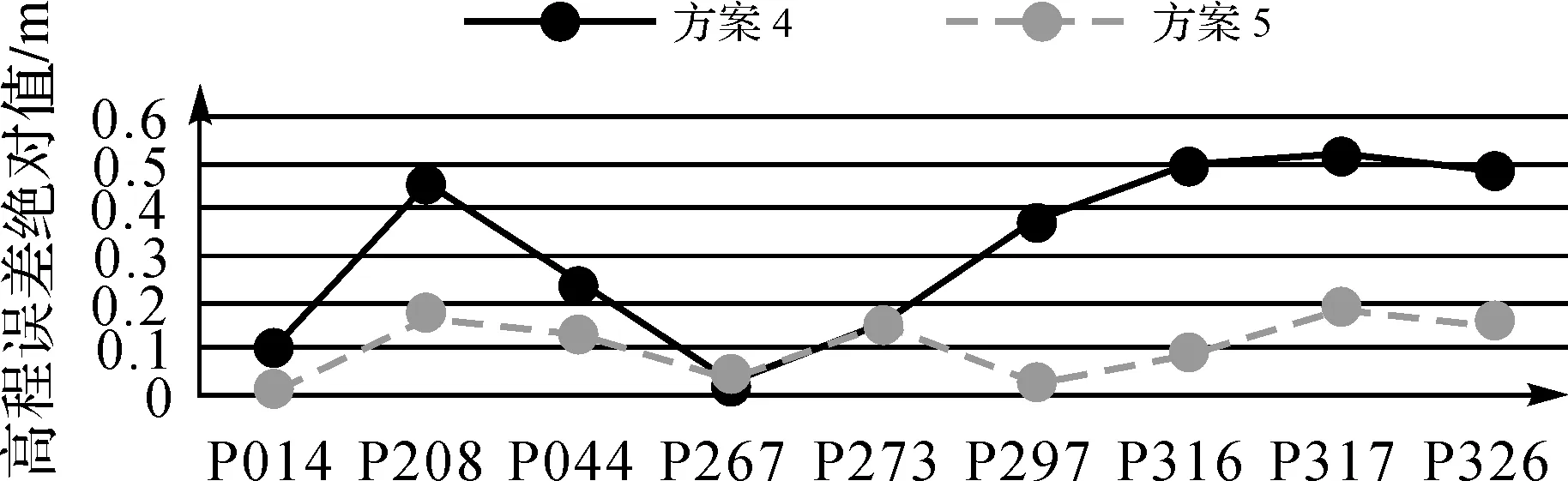
图4 试验2检查点高程误差统计

方案4检查点平面中误差为0.103 m，高程中误差为0.365 m；方案5检查点平面中误差为0.163 m，高程中误差为0.129 m。

试验3选用四角加中间共八控制点方案，2种方案均采用差分GPS辅助区域网平差，用相机自检校功能进行畸变差纠正，只是方案6采用常规航摄航线进行区域网平差，方案7加入5条构架航线参与区域网平差。试验3的2种方案各检查点高程误差绝对值统计如图5所示。方案6检查点平面中误差为0.234 m，高程中误差为1.03 m；方案7检查点平面中误差为0.137 m，高程中误差为0.07 m。

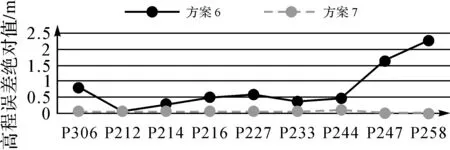
图5 试验3检查点高程误差统计

由以上试验可以看出：

(1) 无论是空三前畸变纠正影像还是空三时进行相机自检校，只要经过畸变差纠正，其区域网平差的高程精度明显优于未纠正畸变的原始影像平差，且高程精度变化相对平稳，原始影像平差的高程误差随机性较大。

(2) 事前畸变差纠正与相机自检校在平面精度和高程精度上相差不大，但相机自检校方便快捷，有着更高的工作效率优势，对于应急测绘保障有着更积极的作用。

(3) 无人机自带GPS本身误差较大，导致成图精度不高，差分GPS辅助光束法区域网平差的高程精度提升明显。使用无人机进行大比例尺航摄时，应尽量选用带差分GPS设备的无人机平台。如果无差分GPS，可尝试精密单点定位技术GPS辅助空三[14]，以提高高程精度。

(4) 对于条带形状测区，构架航线可以大幅提升其高程精度，尤其是条带两端的高程精度。因此在进行带状图无人机航摄时，保证航程的前提下尽量采用构架航线，不仅可以提高高程精度，还能有效减少外业控制点数量。

3 结 语

本文通过对基于非量测相机的无人机航摄系统理论研究与试验，分析了相机检校、差分GPS和构架航线对无人机测绘大比例尺地形图高程精度的影响，论证了相机检校、差分GPS和构架航线可以有效提高区域网平差高程精度，在生产中推广应用有着积极意义。本文只讨论了3种方法各自的作用，并未讨论多方法对区域网平差的影响，也未将这些方法提高高程精度进行量化，这些工作可在下一阶段继续研究。