考虑信用销售的改良品联合采购决策

张云丰，王 勇，龚本刚，但 斌

(1.重庆大学经济与工商管理学院，重庆 400030；2.安徽工程大学管理工程学院，安徽 芜湖 241000)

1 引言

信用销售是企业通过分期付款、延期付款等方式向单位或个人销售商品或服务的交易方式，是市场经济中商品交易的基本形态，是生产经营者相互之间、以及生产经营者与消费者之间直接信用的重要形式[1]。在市场竞争日益激烈的背景下，信用销售方式作为企业提升竞争力、扩大销售和经营规模的主要手段，受到越来越多的企业青睐。早在2009年，商务部、财政部等五个部门就联合发布《关于推动信用销售健康发展的意见》，鼓励企业积极发展信用销售，同时采取措施以加强对信用销售的融资支持。有数据表明，目前美国的信用销售比例高达90%，信用消费占总消费的2/3左右，日本的信用消费占总消费的1/3以上，我国的信用销售比例在40%左右。可见，信用销售在贸易实践中已有较广泛的应用。

在信用销售的理论研究上，Goyal[2]首次将延迟支付引入EOQ模型，奠定了这一领域的研究基础；Aggarwal等[3]将Goyal[2]的EOQ模型拓展到易变质品的情形；Jamal等[4]研究了允许缺货时易变质品在延迟支付条件下的最优库存策略；Huang[5]考虑了零售商上下游同时存在延迟支付的两级信用销售问题；Liao[6]建立了两级信用销售下易变质品的EPQ模型；Min Jie等[7]将Liao[6]拓展到需求依赖于现有库存的情形；Teng等[8]研究了产品处于生命周期成长阶段的信用销售问题；Chen等[9-10]讨论了不同信用条件下零售商的最优EOQ和EPQ问题；Liao等[11]研究了两级信用销售下存在容量约束的易变质品最优订货策略；Mahata[12]考虑了两级信用销售下存在违约风险时易变质品零售商的最优信用周期决策问题。上述文献主要研究了信用销售下的单个厂商库存优化。

近年来，学者们开始重视信用销售对供应链的激励作用，研究企业如何制定合理的信用销售政策以协调整个供应链。Luo Jianwen[13]首次将信用销售作为供应商的一个激励变量，研究了确定型需求下信用销售对供应链的协调作用；Sarmah等[14]利用信用销售条款建立了供应链利益再分配机制以协调各方的利润目标；骆建文[15]分析了需求依赖价格时信用销售对供应链的协调，并比较了信用销售激励机制与数量折扣激励机制；Luo Jianwen等[16]进一步研究了资金成本信息对称与不对称情形下的供应链信用销售协调机制；Arkan等[17]和曾顺秋等[18]探讨了可控提前期下存在信用销售的供应链协调问题；曾顺秋等[19]设计了价格折扣和信用销售组合契约下的供应链协调机制。

改良品是一类特殊的物品，它与普通物品的不同之处在于，当不考虑需求产生的影响时，改良品在持有期间会随着时间的推移发生质量改善、数量增长或重量增加的现象，从而使物品的经济价值或效用得到提升。现实中有许多改良品的例子，如养殖场的生猪、鸡、鸭、鹅等家禽，鱼塘中饲养的鱼，培植的蔬菜、水果，农庄储存的葡萄酒等。Hwang注意到这种现象并首次构建一个改良品EOQ库存模型[20]；随后，学者们分别从不同角度，如考虑通货膨胀、常系数及两参数威布尔净改良率、部分延迟订货、供应链协调等，研究了改良品订货问题[21-29]。Wee等[30]指出少量的改良品订货可凭直觉或经验完成而影响不大，对大规模的改良品订货问题，按照科学合理的方法进行是非常必要的；Chou等[31]指出改良品在存储期的特点与易变质品相反，其订货问题值得进行深入研究。

迄今为止，尚未见考虑信用销售的改良品订货的研究成果。本文以现有基本理论与实践背景为支撑，在众位学者研究的基础上，构建信用销售模式下的改良品订货决策模型。需要说明的是，第一，虽然改良品在存储期间的特点与易变质品相反，但两者的订货模型却存在较大差异。与易变质品不同的是，零售商需要为改良品在存储期间的改良支付改良成本，因而，改良成本的大小将对改良品的订货批量产生重要影响。第二，现有文献在净改良率的设置上主要有常系数和服从两参数威布尔分布两种，但都没有应用数据进行实证检验。笔者以为，对于不同种类的改良品，其改良的规律也不尽相同，因而上述两种净改良率的设置都存在一定的合理之处。

2 基本假设与符号说明

2.1 基本假设

本文在以下基本假设的基础上建立改良品联合采购决策模型：

(1)二级改良品供应链由单个供应商和n个零售商构成；(2)只涉及一种改良品的采购活动；(3)每位零售商的市场需求率已知且稳定不变； (4)不允许缺货，即缺货费用无穷大；(5)补货可视为瞬时完成，提前期忽略不计；(6)每位零售商独立采购时具有相同的订货成本；(7)考虑无限个订货周期的情形；(8)改良品的净改良率为常系数；(9)供应商向零售商提供延迟支付作为信用销售手段。

2.2 符号说明

本文建立改良品联合采购决策模型中设定的主要符号和含义说明如下：

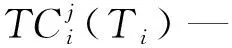
3 模型

零售商i在一个订货周期内的库存水平受市场需求和改良品自身改良的共同影响，从最大值Qi逐渐减小到零，任意时刻t的库存水平可用微分方程表示为:

(1)

解之得

(2)

因此，零售商i每次的订货批量为:

(3)

由式(3)可知，当改良品的市场需求率Di和净改良率λ恒定时，零售商i的订货批量Qi与订货周期Ti之间存在一一对应关系。这种情形下，在构建改良品采购决策模型时，以订货周期而非订货批量作为决策变量将会更为方便。因此，下文将选择订货周期作为决策变量。每一个零售商都面临着独立采购与联合采购两种采购方式，而零售商选择某种采购方式的原因在于该采购方式能够节约更多的总成本。接下来，我们分别建立零售商独立采购与联合采购时的单位时间总成本函数并进行比较，得出零售商选择联合采购的条件。

3.1 独立采购

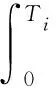
(1)若Ti≤M，则

(4)

(2)若Ti≥M，则

(5)

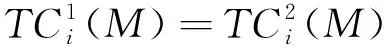
对式(4)-(5)直接求最优解比较困难，为此参考王勇等[26-29]的处理方式，当λTi<<1及λ(Ti-M)<<1时，对上述指数函数进行泰勒展开，并取其前三项，得到：

(6)

(7)

命题1 令Δ1=2K-(hi-λc+λω+pir2)DiM2。(1) 若Δ1≤0，则零售商i的最佳订货周期、最小单位时间总成本分别表示为：

(8)

(2)若Δ1≥0，则零售商i的最佳订货周期、最小 单位时间总成本分别表示为：

(9)

证明 参考附录命题2的证明。

3.2 联合采购

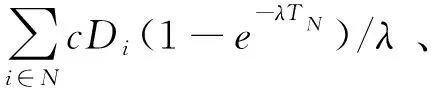
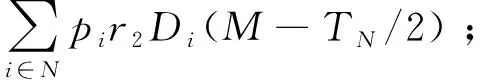
(10)

(11)

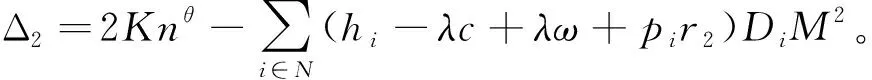
(1)若Δ2≤0，则采购联盟N的最佳订货周期、最小单位时间总成本分别为：

(12)

(2)若Δ2≥0，则采购联盟N的最佳订货周期、最小单位时间总成本分别为：

(13)

证明 见附录。

由命题1和命题2得到下列推论。

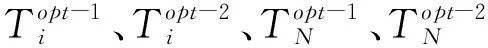
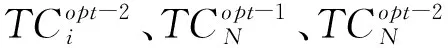
推论3 对于两种采购方式，都存在最短延迟支付期限Mmin，当且仅当供应商提供的延迟支付期限M>Mmin时，延迟支付下的最小单位时间总成本才会更低。其中，若Δ2≤0，

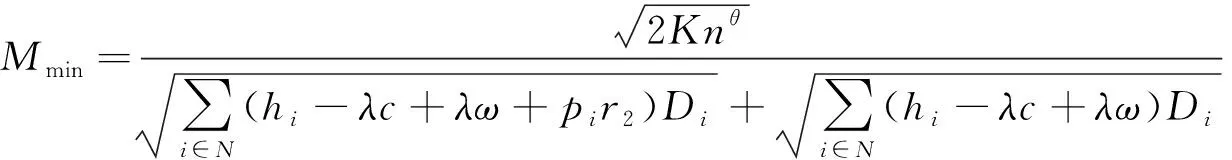
若Δ2≥0，

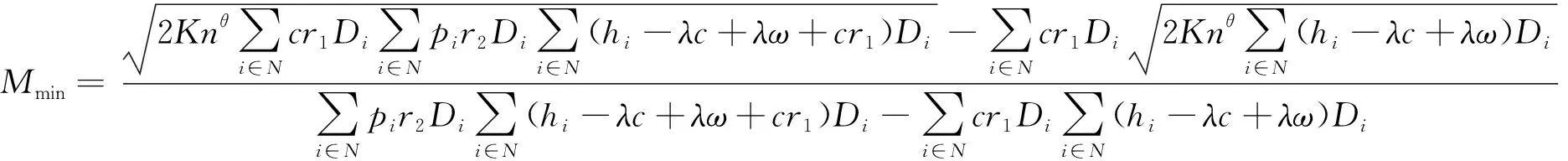
(N=1时表示独立采购)。

3.3 两种采购模式比较

在由单个供应商和n个零售商构成的二级改良品供应链中，零售商独立采购与联合采购时的最小单位时间总成本差值表示为：

(1) 若Ti≤M，TN≤M，则

(14)

(2)若Ti≥M，TN≤M，则

(15)

(3)若Ti≥M，TN≥M，则

(16)

当ΔTC>0时，表明零售商们组建采购联盟N，实施联合采购是有利可图的，因此，联合采购是占优的策略；当ΔTC<0时，则至少有一位零售商在联合采购中成本上升，并将退出采购联盟N。令Ai=(hi-λc+λω+pir2)Di，Bi=(hi-λc+λω+cr1)Di，Γi=(cr1-pir2)DiM2，由式(14)-(16)可知，当订货成本协调指数θ满足：

(17)

时，n位零售商联合采购的最小单位时间总成本小于独立采购的最小单位时间总成本之和，联合采购优于独立采购。

4 联合采购博弈分析

4.1 问题描述

为了保证联合采购顺利实施，必须合理分配联合采购产生的最小单位时间总成本，确保每位零售商在联合采购中分配的成本都不会比独立采购时大，这样才能让每位零售商有动力参与联合采购，从而实现最小单位时间总成本的节约。

本文以联合采购的最小单位时间总成本作为分配对象，应用多人合作博弈理论，将联合采购的成本分配问题转换成联合采购博弈。以N={1，2，…，n}表示n个零售商的集合，称为全联盟。函数Φ:2N→R为分派给任意非空子联盟S⊆N的特征函数，且Φ(φ)=0，Φ(S)称为联合采购博弈(N,Φ)中子联盟S的成本。联合采购博弈的主要问题是在全联盟建立后，如何在各零售商之间分配联盟总成本Φ(N)。

定义1 对任意的S⊆N，子联盟S的成本是最小化联盟在联合采购时所产生的单位时间总成本。在供应商提供延迟支付期限M作为信用销售手段时，改良品联合采购博弈(N,Φ)可定义为：

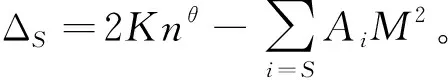
4.2 博弈基本性质

性质1 对任意的S⊂V⊆N，满足TS>TV。

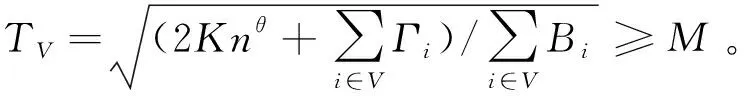
矛盾。因此，有TS≥TV成立。

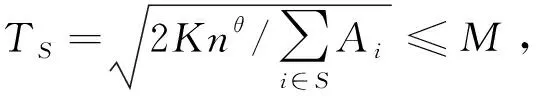
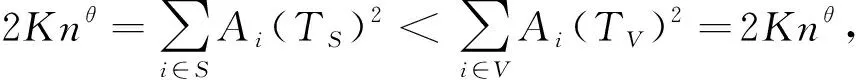
性质1意味着规模越大的采购联盟的最佳订货周期越短。因此，单位改良品在持有期间的改良量也越少，每个零售商的平均库存水平也越低，单位时间承担的库存成本也越低。

性质2 对任意的S，V⊆N，满足Φ(S)+Φ(V)≥Φ(S∪V)。

证明(1)若ΔS≥0，ΔV≥0且ΔS∪V≥0，则由性质1知TS≥TS∪V，TV≥TS∪V。结合定义1，得到

(2) 若ΔS≥0，ΔV≥0且ΔS∪V≤0，则由性质1知TS≥M≥TS∪V，TV≥M≥TS∪V。结合定义1，得到：

(3)若ΔS≥0，ΔV≤0且ΔS∪V≤0，则由性质1知TS∪V≤TV≤M≤TS。结合定义1，得到：

(4)若ΔS≤0，ΔV≥0且ΔS∪V≤0，则由性质1知TS∪V≤TS≤M≤TV。结合定义1，得到：

(5)若ΔS≤0，ΔV≤0且ΔS∪V≤0，则由性质1知TS∪V≤TS≤M及TS∪V≤TV≤M。结合定义1，得到：

性质2表明联合采购博弈(N,Φ)具有次可加性，合作是有益的。因此，对各零售商而言，联合采购的最小单位时间总成本将少于独立采购的最小单位时间总成本之和。

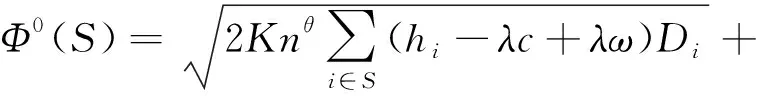
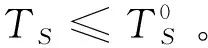
证明 (1) 若ΔS≤0，则

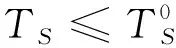
性质3意味着，当供应商允许零售商延迟支付货款时，采购联盟将缩短订货周期。如此情形下，零售商的平均库存水平下降，同时单位改良品在持有期间的改良量也减少。

对于联合采购博弈(N,Φ)来说，若每个零售商获得的最小单位时间总成本分配解ψ=(ψ1，ψ2，…，ψn)满足：

(18)

则ψ=(ψ1，ψ2，…，ψn)属于联合采购博弈(N,Φ)的核心。核心是合作博弈重要的解概念，属于核心的分配解使得任何零售商及子联盟不愿脱离大联盟。Deng Xiaotie等[33]指出对许多合作博弈而言，得到一些解都是NP难题，因此人们对合作博弈的研究重点放在一些具有良好性质的博弈上，如子模博弈、拟凹博弈等。即便如此，证明延迟支付下的联合采购博弈是子模博弈或拟凹博弈，也是十分困难的。下面给出当延迟支付满足特定条件时，联合采购博弈所具有的性质。

性质4 对任意的i∈N，若满足cr1=pir2，即零售商每一单位产品的利息支出与利息收入相等，则延迟支付契约下的改良品联合采购博弈(N,Φ)是子模博弈。

证明 若对任意的i∈N，满足cr1=pir2，则Φ(S)表示为：

对任意的S⊂V⊂N{l}，

因此，博弈(N,Φ)是子模博弈。

性质4表明，零售商对所属联盟的边际成本随着联盟规模的增大而减小，任意一个零售商或子联盟加入另一个不相连联盟的动机随着联盟成员的增多而增大，各零售商有动机构成大联盟。

子模博弈的核心非空且是其边际向量的凸组合，夏普利值是核心的重心，然而核心是一个集合概念，并不是唯一的分配方案，且夏普利值的计算比较复杂，随着联盟参与人数的增加，其计算复杂度呈指数型增大[34]。因此下文将设计一种属于核心且易于计算的单值成本分配方案。

4.3 联合采购博弈成本分配

考虑到全联盟N的最小单位时间总成本与Δ2的正负有关，因此将联合采购博弈(N,Φ)的分配解表示为分段函数。

(1)若Δ2≤0，全联盟N的最小单位时间总成本Φ(N)表示为：

(2)若Δ2≥0，全联盟N的最小单位时间总成本Φ(N)表示为：

命题3 (1) 当Δ2≤0时，令

则ψ=(ψ1，ψ2，…，ψn)∈Core(Φ)；

(2)当Δ2≥0时，令

ψj=

则ψ=(ψ1，ψ2，…，ψn)∈Core(Φ)。

证明 (1)

对任意的S⊆N，若ΔS≤0，则

若ΔS≥0，则

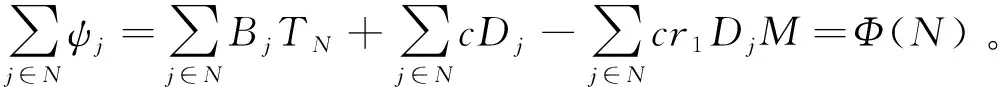
对任意的S⊆N，

命题3表明，成本分配方案ψ是一个公平且稳定的分配方案，这时没有任何零售商从全联盟中撤出构成自己的联盟，没有任何一个子联盟有动机从全联盟中分离出来。

5 数值算例

下面通过一个算例来帮助大家更好地理解本文的结论。在由单个供应商和三位零售商组成的二级改良品供应链系统中，我们设置相关参数如下：D1=1800、D2=2000、D3=2200；h1=4.6、h2=4.4、h3=4.2；c=10；p1=16、p2=15、p3=14；θ=0.5；ω=12、λ=0.2；M=0.2；r1=0.1、r2=0.05；K=100(ΔS≤0)，K=500(ΔS≥0)。

5.1 算例求解

将上述各项参数代入式(17)进行检验，易知当θ=0.5时，三位零售商联合采购优于独立采购。设三位零售商协议组成采购联盟，统一订货周期，向改良品供应商进行联合采购，则N={1,2,3}，S可取{1}、{2}、{3}、{1,2}、{1,3}、{2,3}或{1,2,3}。考虑ΔS≤0和ΔS≥0两种情形，结合所设置的参数，得到计算结果如下表1所示。

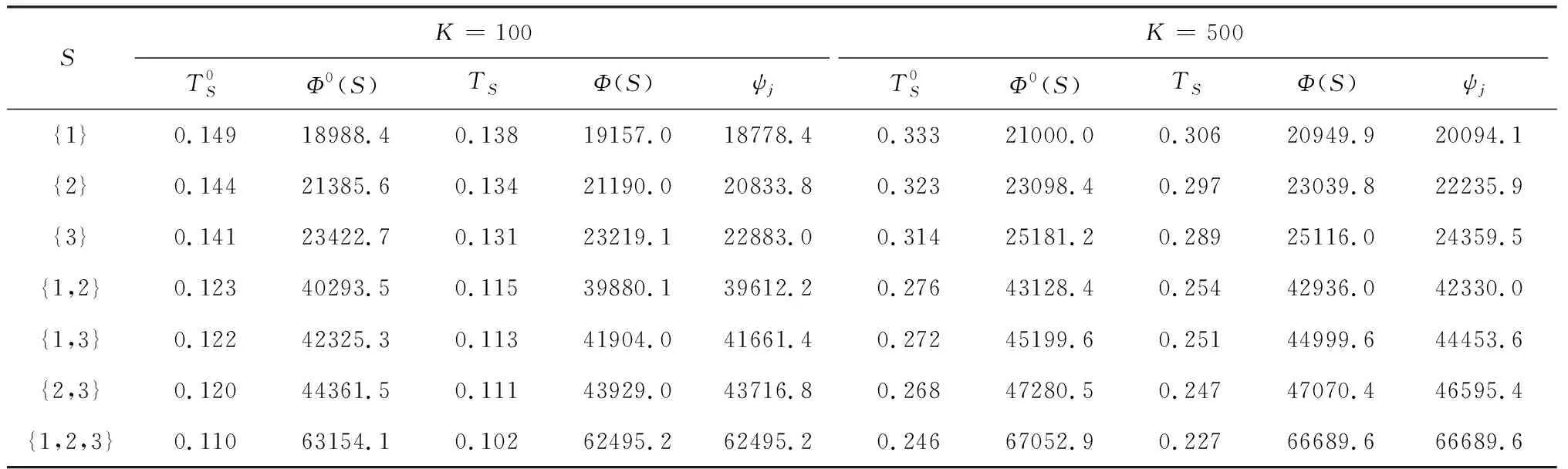
表1 采购联盟的订货周期与单位时间总成本

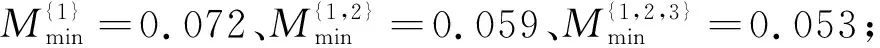
5.2 敏感性分析

下面分别考虑净改良率λ、单位改良成本ω、延迟支付期限M发生变动时，对采购联盟订货周期、最小单位时间总成本及成本分配方案ψ的影响。由于ΔS≤0和ΔS≥0时需依据不同的公式进行计算，因此在作敏感性分析时，我们仍然分别考虑K=100和K=500两种情形。计算结果如表2～表4所示。

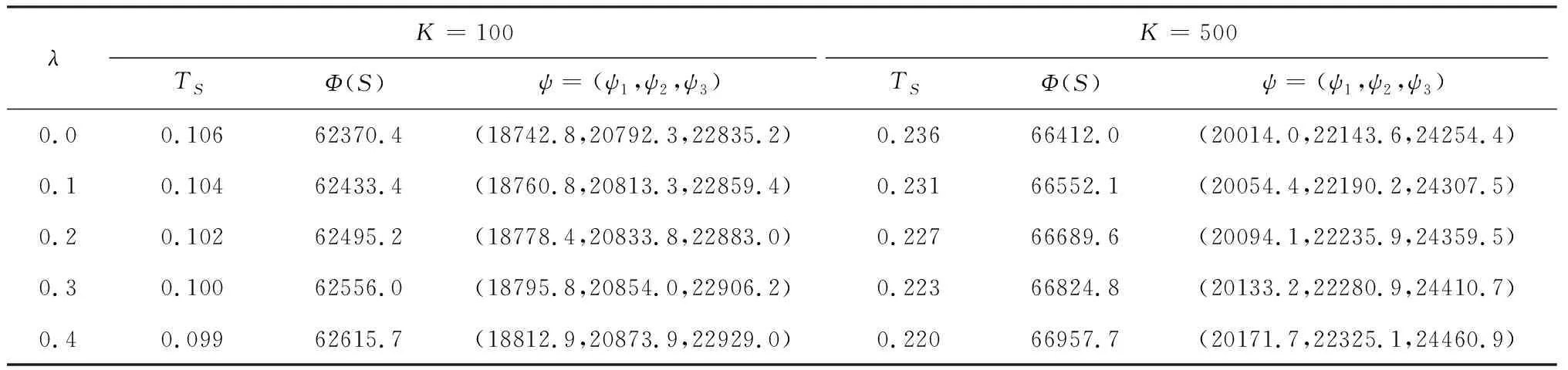
表2 净改良率的敏感性分析

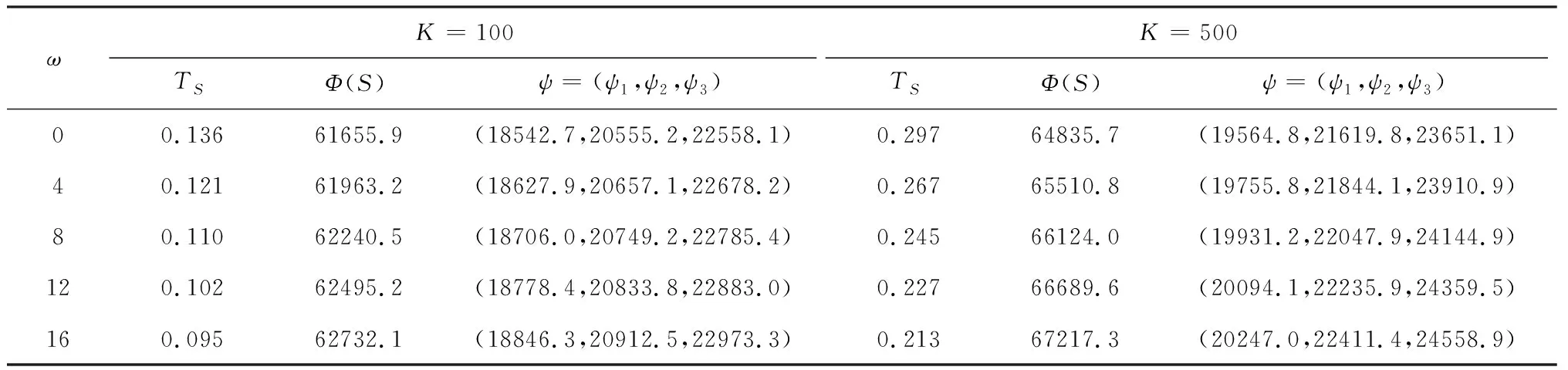
表3 单位改良成本的敏感性分析

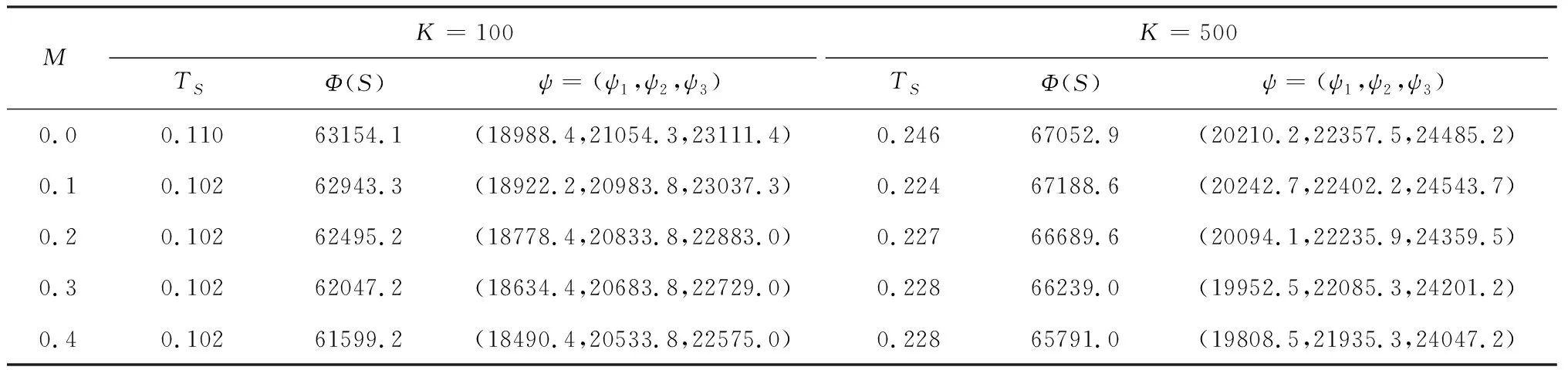
表4 延迟支付期限的敏感性分析

从表2数据可以看出：采购联盟的最佳订货周期随着净改良率的增大而减小，最小单位时间总成本随着净改良率的增大而增加。由于单位产品改良成本大于批发价格，因而为获得单位改良品，通过改良方式而不是直接采购支付的成本更大。随着净改良率增大，单位时间内改良量越来越多，致使最小单位时间总成本也逐渐增加。零售商希望通过缩短订货周期来减少改良量从而降低最小单位时间总成本，但会引起单位时间订货成本相应增加。在此约束下，零售商的最佳订货周期减小程度非常有限。由成本分配的结果可知，净改良率增大引起的最小单位时间总成本增加量会分摊到每个零售商，且最小单位时间总成本较大的零售商承担的增加量也会多一点，体现了该成本分配方案的公平性。

从表3数据可以看出：采购联盟的最佳订货周期随着单位产品改良成本的增大而变小，而最小单位时间总成本随着单位产品改良成本的增大而增加，每位零售商分配的最小单位时间总成本也随之增加。在单位产品改良成本逐渐增大的过程中，相比于直接采购，通过改良获得单位产品所能节约的成本越来越小。当单位产品改良成本大于单位产品批发价格时，改良单位产品支付的成本比直接采购更大，零售商宁愿通过直接采购而不是产品改良来满足需求。

从表4数据可以看出：在延迟支付期限较小时，采购联盟的最佳订货周期随着延期支付期限的增加而变大，而当延迟支付期限增加到某一特定值时(令ΔN=0，可解出当K=100时，有M=0.102；当K=500时，有M=0.228)，最佳订货周期趋于稳定保持不变。最小单位时间总成本随着延迟支付期限的增加而逐步减少，这是由于随着支付期限的延长，采购联盟需要支付给供应商的利息减少，同时销售收入可以获得更多的利息。在采购联盟的最小单位时间总成本逐渐减少的影响下，每位零售商分配的最小单位时间总成本也依次减少。

6 结语

随着经济全球化和信息技术发展，越来越多的企业意识到采购管理在企业经营管理中的地位和作用，企业间实施联合采购可以降低采购成本，增加竞争优势，提高与上级供应商的谈判议价能力。改良品的订货问题普遍存在却又容易被忽视。文献[29]对改良品的联合采购问题进行了初步探索。本文的研究与张云丰等[29]的区别在于，首先，本文考虑了现实交易中应用非常广泛的信用销售对零售商采购的影响；其次，本文设计的采购联盟订货协调成本函数更符合实际，即随着联盟规模的增大，零售商加入联盟的边际协调成本是递减的。文中给出联合采购优于独立采购的条件，并将改良品联合采购成本分配问题构造成联合采购博弈。同时，证明了联合采购博弈的几点性质，并通过数值算例给予验证。本文的研究对现实中从事改良品销售的企业制定最佳补货策略具有一定的理论指导意义。在将来的研究中还可以对本文作进一步拓展，如在零售商实施联合采购时供应商提供数量折扣激励以及零售商采购多种产品的情形。另外，现实中零售商允许客户延迟支付也是十分常见的现象，因此两级信用下的多零售商联合采购改良品问题值得深入研究。

附录：

采购联盟的单位时间总成本函数表示为：

(1)若TN≤M，则

(2)若TN≥M，则

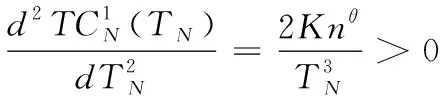
(2)当TN≥M时，有

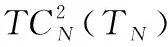
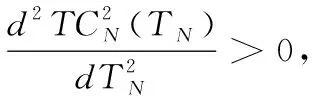
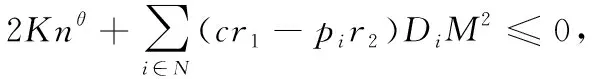
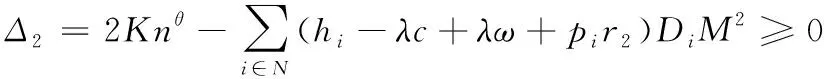
由上面分析可知命题2成立。当N=1时，联合采购退化为独立采购，上述分析过程即为命题1的证明过程。