滑雪板夹角对跳台滑雪飞行阶段气动特性的影响

胡 齐，陈 骐，张文毅



滑雪板夹角对跳台滑雪飞行阶段气动特性的影响

胡 齐1，陈 骐1，张文毅2

1.国家体育总局体育科学研究所, 北京 100061; 2.北京体育大学, 北京 100084

目的：分析研究滑雪板夹角对跳台滑雪飞行阶段气动特性的影响。方法：建立精细化三维几何模型与网格模型，采用部分时均（partially averaged Navier-Stokes，PANS）湍流模型对气动特性进行计算流体力学（computational fluid dynamics，CFD）数值模拟，获取不同滑雪板夹角下（24°、28°、32°、36°和40°）力和力矩、压力分布以及流场形态。结果：1）总升力与总阻力、升力系数与阻力系数、总力矩与滑雪板力矩均随滑雪板夹角增大先减小后增大最后小幅减小，但总升阻比基本保持不变，总体呈略微下降趋势；2）滑雪板升力随滑雪板夹角增大呈现单调递增的趋势，而滑雪板阻力随滑雪板夹角增大先减小后增大；3）滑雪板正面压力分布规律基本相同且比较均匀，而滑雪板背面下半部分压力随滑雪板夹角变化比较明显；4）运动员身后以及滑雪板身后的流场形态主要以回流涡形式出现，滑雪板背面回流涡结构明显比运动员身后复杂得多，而且回流涡强度也明显大得多。结论：1）滑雪板夹角变化对总升阻比影响很小，但对总升力、总阻力、升力系数以及阻力系数产生一定影响，同时对运动员气动特性也产生一定影响。2）滑雪板气动特性在运动员/滑雪板整体系统中起着更为重要作用，不仅要关注运动员身体姿态，而且应更加关注滑雪板姿态；3）总力矩大小和滑雪板力矩大小随滑雪板夹角变化趋势一致，而且滑雪板力矩在总力矩中始终占据主导地位，选取合适的滑雪板夹角对飞行阶段稳定性至关重要，建议优选的滑雪板夹角范围为24°~32°。

气动特性；跳台滑雪飞行阶段；滑雪板夹角；计算流体力学；V型

1 前言

整个跳台滑雪过程通常依次分为4个不同的阶段：助滑、起跳、飞行和着陆，空气动力学在这4个阶段中均起着重要的作用。在起跳后，运动员应在飞行阶段早期尽快达到一个稳定的飞行位置，并确保受到小阻力[13]，同时应完成向后旋转和向前旋转角动量的完全平衡[16]。跳台滑雪运动员在0.5s内完成飞行姿态的稳定[21]，并且在这个短时间内（约为15 m的飞行距离），很有可能运动员不能进行任何有意的姿态调整，可以说起跳阶段决定随后的飞行姿态。同样，这也意味着起跳时所发生的错误不能在飞行阶段得到有效纠正，但成功起跳的优势可能会因飞行过程中错误而丧失。一般来说，飞行阶段被认为是整个跳台滑雪过程中气动特性体现最为明显的阶段。诸多对跳台滑雪飞行阶段气动特性研究文献[2,5,6,8-10,12,17,18,20]采用了风洞试验测量或计算机模拟与现场测量相结合等方法。普遍认为，滑雪器材（滑雪板和滑雪服）在跳台滑雪飞行阶段的作用不可忽略。与以往的滑雪板平行飞行方式相比，V型飞行方式具有更好的气动性能，使运动员能够更多地向前倾斜[19,20]。近年来，为了使气流经过滑雪板更加平缓，在飞行过程中滑雪板姿态越来越受到人们的关注。Virmavirta等[22]通过风洞试验研究单个滑雪板空气动力特性，将滑雪板悬挂在六分量风洞平衡测量装置上，这种试验研究方法或多或少偏理想化，显然并不是所有的结果都适用于真实飞行阶段。

上述这些方法均不能直观地显示或分析运动员周围的流场。能够在运动过程中分析气动力、显示压力分布和详细流场信息的另一种技术是计算流体力学（CFD），该技术最近被应用于自行车和游泳等运动中。CFD不需要物理装置，成本低，可以模拟大多数物理现象，只需一次模拟就可以收集大量的数据。尽管CFD已经被认为是未来跳台滑雪空气动力学研究的重要工具，但迄今为止发表的CFD相关研究较少[1,3,4,7,14,15]，尤其是针对飞行阶段就更少[1,4,7,14]。Keizo等[3]人采用CFD技术研究了跳雪运动员在起跳过程中姿态对气动特性的影响，着重比较两种不同跳跃者的起跳情况，结论认为，起跳过程中气动力特性在较短的时间内发生了动态变化，两种起跳方式的气动力特性差异较大。Gardan等[1]人采用CFD方法来探讨迎风角和速度对气动力的影响，数值结果表明，在早期飞行阶段速度对升力系数和阻力系数的影响很小，相反，迎风角变化对作用于运动员身体上的升力和阻力有很大的影响。

综上所述，国内、外报道姿态与跳台滑雪飞行阶段气动特性的CFD研究主要集中于运动员身体姿态，鲜有报道滑雪板姿态的CFD研究[7,14]，即使有也仅是涉及而已。本研究拟建立运动员/滑雪板整体系统的精细化三维几何模型与网格模型，采用PANS湍流模型进行CFD数值模拟，获取不同滑雪板夹角下力和力矩、压力分布以及流场形态，分析研究V型飞行方式滑雪板夹角对跳台滑雪飞行阶段气动特性的影响。

2 研究对象与方法

2.1 研究对象

研究对象为跳台滑雪运动员/滑雪板整体系统。根据Müller等[9]人统计分析结果，跳台滑雪运动员的身体形态特征选取平均值，即身高为177 cm，身体质量指数（BMI）为19.5，躯干（坐高）与身高比值0.532，滑雪板长度258 cm，宽11.5 cm。

2.2 研究方法

2.2.1 控制方程

本研究采用大涡模拟技术，该技术对预测钝体周围的流动分离有优势。为了获得更精确的结果，采用了PANS湍流模型，其控制方程表达式如下：

式中i为已分解流场速度，为时间，为流体密度，为介质粘性系数，为湍流粘性系数，f为未分解湍动能比率，为未分解湍动能耗散率比率，k为未分解局部时均化湍动能，为未分解局部时均化湍动能耗散率。

其中：

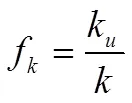
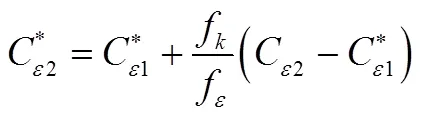
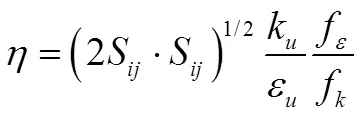
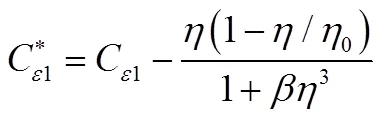
采用有限体积法对控制方程进行离散计算，压力和速度的耦合采用SIMPLEC算法，时间采用二阶差分格式进行离散，湍动能以及速度项采用二阶迎风格式，时间步长为0.000 1 s。

2.2.2 模型建立与网格无关性验证

根据研究对象特征，建立跳台滑雪运动员/滑雪板整体系统的三维实体模型，对运动员的身体特征进行精细化建模，手指、耳朵、眼罩、面部特征可以从图1中清晰分辨。

图1 运动员/滑雪板整体系统精细化实体模型图

Figure 1. The Refined Solid Model of the Whole Athlete/Skis System

注：左图为正视图，右图为侧视图。

跳台滑雪运动员/滑雪板整体系统计算区域的尺寸大小为长13.5 m、宽5 m、高6 m，如图2所示。采用商用前处理软件ICEM对计算区域进行四面体网格离散，在计算区域中心对称面上体积网格分布和运动员表面网格分布如图3所示。运动员模型的表面网格分辨率最小达到0.5 mm。对于体网格，在运动员周围区域配置了较细的网格单元，以高精度捕获尾流结构。另一方面，为了降低计算量，较粗的网格单元被分配到远离运动员的区域。

图2 计算区域示意图

Figure. 2. Computational Domain

图3 网格分布示意图

Figure 3. Mesh Distribution

注：左图为体网格，右图为运动员表面网格。

为了满足PANS模型计算要求，运动员周边采用网格加密，并保证y plus控制在100之内，此控制要求在先前的研究中获得了证实[3]。针对上述网格模型，通过均匀加密选定了4种网格密度，网格点数从800万～2 357万，进行网格无关性验证，验证结果如表1所示。4种网格验证计算获得的升阻比均为1.8。由此可见，即使选定800万网格节点的计算域离散方案，也能够准确预测跳台滑雪运动员/滑雪板整体系统的气动力学性能。

表1 网格无关性验证结果

2.2.3 边界条件与计算工况

边界条件的设置如下：

1）进口设置为速度进口，进口速度根据飞行速度设定；2）出口设置为压力出口，压力为大气压101 325 Pa；3）中间截面为周期性条件；4）其他壁面为无滑移边界条件；5）气体为不可压缩空气；6）在常重力下，重力加速度设置为g0=9.807 m/s2。

跳台滑雪运动员在飞行阶段的姿态参数包括迎风角、滑雪板与速度方向夹角α、滑雪板与身体夹角θ、上半身弯曲角度β、滑雪板夹角λ，如图4所示。Müller等[10,17]人的研究成果给出这些姿态参数通常的取值范围。同时，图5显示了在飞行阶段整个系统受力情况。阻力系数（C）和升力系数（C）的计算方法见公式（11）和（12），为模型的正面投影区域面积。

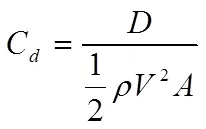
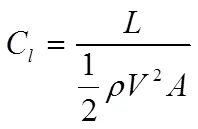
在本研究中，开展了5种不同滑雪板夹角下跳台滑雪飞行阶段动特性和流动结构特性CFD研究。其中，滑雪板夹角λ分别取值为24°、28°、32°、36°和40°，同时迎风角φ=30°、滑雪板与速度方向夹角α=30°、滑雪板与身体夹角θ=16°、上半身弯曲角度β=18°，速度V=29 m/s。据此，为每个滑雪板夹角λ的运动员/滑雪板整体系统生成计算网格，分别进行了CFD数值模拟。

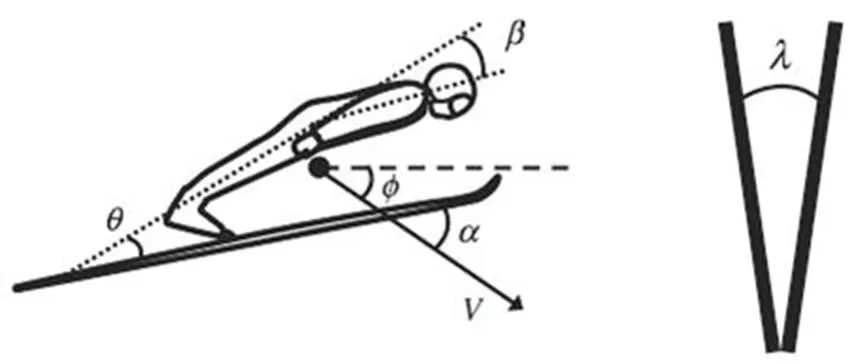
图4 飞行阶段姿态参数示意图

Figure 4. Attitude Parameters in Flight

图5 飞行阶段整体系统受力情况图

Figure. 5. All the Forces Acting on the Athlete/Skis System during Flight Phase

3 结果

3.1 力和力矩

作用于运动员/滑雪板整体系统上的气动力可分为升力和阻力，而且这些力的作用点绝大多数不会在运动员/滑雪板整体系统质心上，因此极有可能会产生相应的力矩。表2列出了不同滑雪板夹角λ下运动员/滑雪板整体系统以及滑雪板的力学特性结果。图6~10显示了运动员/滑雪板整体系统以及滑雪板的力学特性随滑雪板夹角变化曲线。图6和图7中各项力均为作用在运动员/滑雪板整体系统或滑雪板上同一性质的合力。图8中阻力系数与升力系数分别由公式（11）和（12）计算得到。图9中力矩是相对于运动员/滑雪板整体系统质心的力矩，“+”代表力矩作用后使整体系统逆时针旋转，“-”代表力矩作用后使整体系统顺时针旋转。图10中的升阻比由升力除以阻力计算得到的。

不同滑雪板夹角λ下运动员/滑雪板整体系统总升力以及滑雪板升力随滑雪板夹角变化曲线如图6所示。可以看出，总升力随滑雪板夹角增大先减小后增大最后小幅减小，即当夹角不大于28°时，总升力随夹角增大而减小；当夹角大于28°且小于36°时，总升力随夹角增大而增大；当夹角大于36°时，总升力随夹角增大小幅减小。滑雪板升力随滑雪板夹角增大呈现单调递增的趋势，即当夹角不大于28°时，升力随夹角增大而小幅增加；当夹角大于28°且小于36°时，升力随夹角增大而大幅增大；当夹角大于36°时，升力随夹角增大小幅增加。总升力的最大增幅是滑雪板升力的两倍左右。

表2 力学特性结果

图6 升力变化曲线图

Figure 6. Lift Force Changes with Ski Opening Angle

不同滑雪板夹角λ下运动员/滑雪板整体系统总阻力以及滑雪板阻力随滑雪板夹角变化曲线如图7所示。可以看出，总阻力随滑雪板夹角增大变化趋势与总升力一致，即先减小后增大最后小幅减小。滑雪板阻力随滑雪板夹角增大先减小后增大，即当夹角不大于28°时，阻力随夹角增大而减小；当夹角大于28°且小于36°时，阻力随夹角增大而大幅增大；当滑雪板夹角大于36°时，阻力随夹角增大小幅增加。总阻力的最大增幅是滑雪板阻力的两倍左右。

图7 阻力变化曲线图

Figure 7. Drag Force Changes with Ski Opening Angle

不同雪板夹角λ下运动员/滑雪板整体系统阻力系数与升力系数随滑雪板夹角变化曲线如图8所示。不难看出，阻力系数随滑雪板夹角增大变化趋势与升力系数一致，即先减小后增大最后小幅减小，同样与总升力以及总阻力随滑雪板夹角增大变化趋势一致。

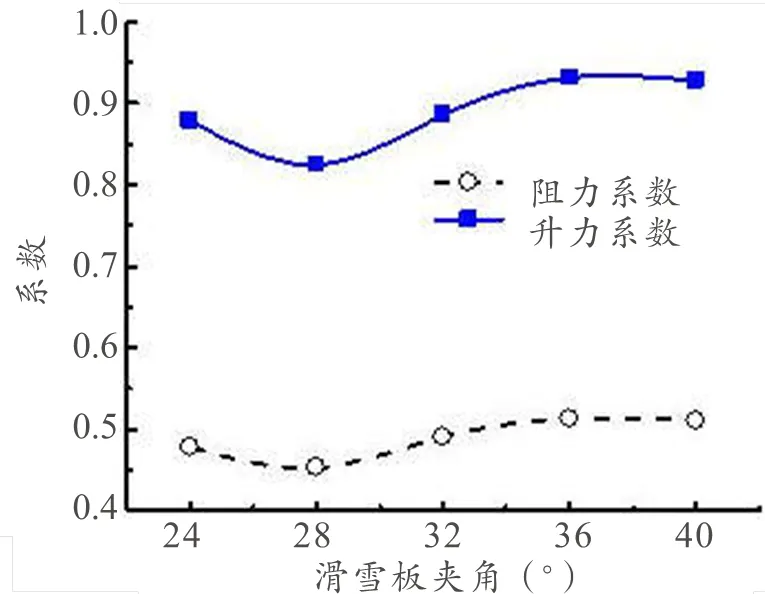
图8 阻力系数、升力系数变化曲线图

Figure 8. Changes of Drag Coefficient and Lift Coefficient with Ski Opening Angle

不同滑雪板夹角λ下运动员/滑雪板整体系统总力矩以及滑雪板力矩随滑雪板夹角变化曲线如图9所示。可以看出，总力矩与滑雪板力矩均是产生逆时针旋转的效果，其总力矩大小和滑雪板力矩大小随滑雪板夹角增大变化趋势一致，即先减小后增大最后小幅减小，同样与总升力以及总阻力随滑雪板夹角增大变化趋势一致。

图9 力矩变化曲线图

Figure 9. Torque Changes with Ski Opening Angle

图10 升阻比变化曲线图

Figure 10. Lift-to-drag Ratio Changes with Ski Opening Angle

不同滑雪板夹角λ下运动员/滑雪板整体系统总升阻比以及滑雪板升阻比随滑雪板夹角变化曲线如图10所示。可以看出，总升阻比随滑雪板夹角增大变化基本保持不变，总体呈略微下降趋势。另一方面，滑雪板升阻比随滑雪板夹角增大先大幅增大（在滑雪板夹角不大于28°之前），之后略微下降。

3.2 压力分布

不同滑雪板夹角λ下运动员/滑雪板整体系统的正面压力分布如图11所示。对于运动员来说，正面压力在不同夹角下分布规律基本一致，高压区主要集中于头部、上半身、胯关节、膝关节等部位，低压区主要集中于身体侧部。同时不难看出，夹角为28°和32°时正面高压区面积偏小，尤其是滑雪板夹角为28°时正面高压区面积明显最小。对于滑雪板来说，正面压力在不同夹角下分布规律基本相同，而且分布比较均匀。

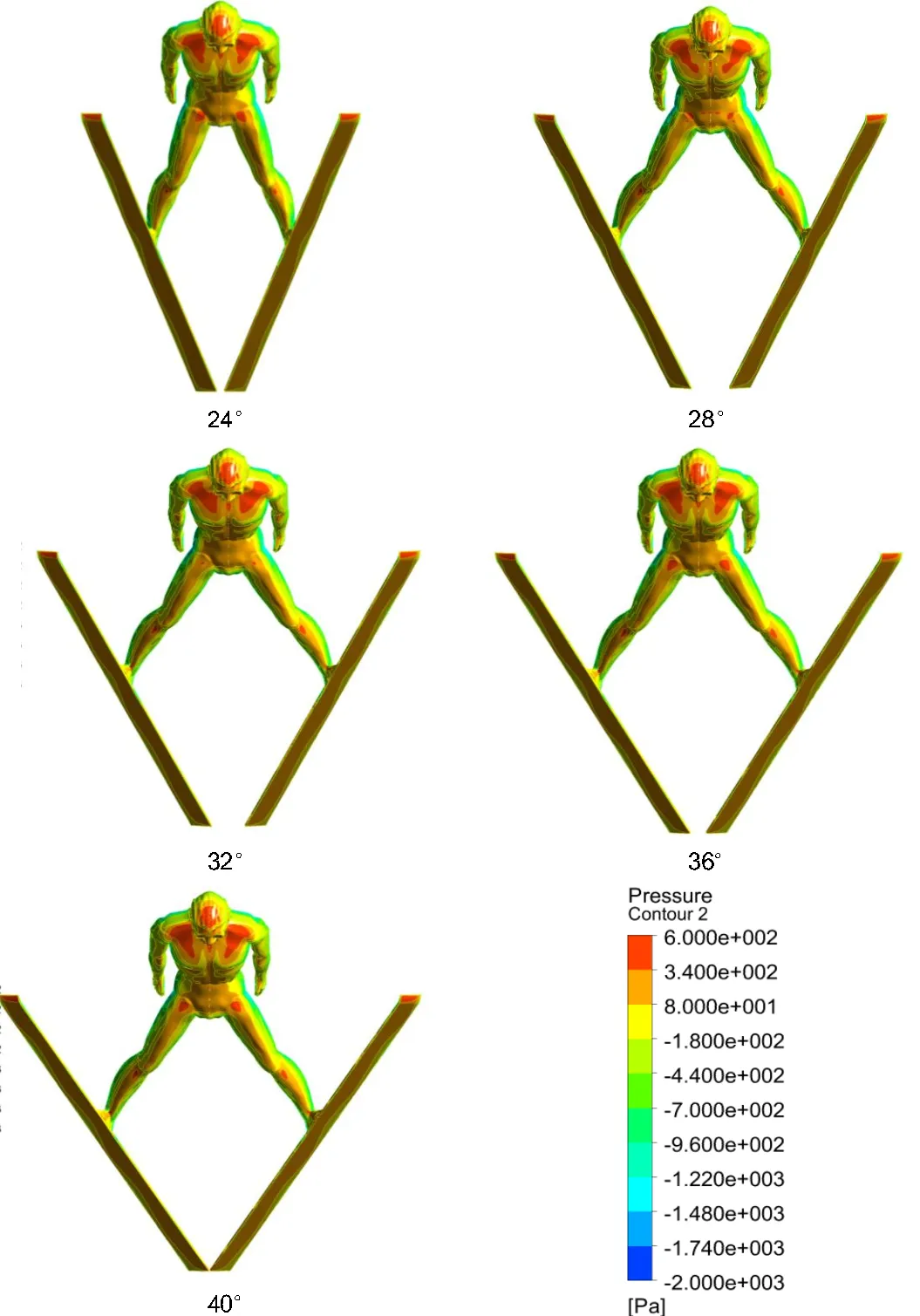
图11 正面压力分布图

Figure 11. Frontal Pressure Distribution

不同滑雪板夹角λ下滑雪板背面压力分布如图12所示。可以看出，高负压区主要集中在滑雪板顶端和中部。进一步可看出，滑雪板背面上半部分的压力随滑雪板夹角变化比较细微，然而滑雪板背面下半部分压力变化比较明显。

图12 滑雪板背面压力分布图

Figure 12. Pressures Distribution of the Ski Back

3.3 流场形态

不同滑雪板夹角λ下涡流形态和气流速度流线如图13所示，左边为背面正视图，右边为侧视图。运动员身后以及滑雪板后面的涡流形态均主要以回流涡结构形式出现，此结构会加速能量耗散。对于运动员来说，其身后主要产生2对涡结构，分别在肩与上臂结合处以及腰与胯结合处的后方，当夹角为28°时，身后的回流涡结构强度最低。对于滑雪板来说，无论角度是否改变，其后侧有6对涡结构产生，当夹角为28°时，后侧的回流涡结构强度也相对最低，之后随着夹角增大，其后侧的回流涡结果变得更加无序，尤其是滑雪板下半部分的后侧。不难看出，当夹角为24°时，运动员腰与胯结合处后方的回流涡结构强度较小，涡流尺度较大的区域主要集中在滑雪板后侧；当夹角大于28°时，运动员身后的回流涡强度高于滑雪板后侧，在腰与胯结合处后方形成尺度较大的回流涡。同时，观察到在负压力梯度作用下，气流速度在运动员以及滑雪板上均发生了流动分离，尤其是在滑雪板下半部分。当夹角为24°时流动分离程度以及尾迹尺寸明显最大，当夹角为28°时流动分离程度以及尾迹尺寸明显最小，当夹角大于28°时流动分离程度以及尾迹尺寸逐渐变大。

4 讨论

本研究中，所获得的气动特性部分结果与Gardan等[1]人的部分研究结果相似。通过总结风洞试验测量结果以及数值计算结果，他们公布了迎风角为29°、滑雪板与身体夹角θ为17.4°、上半身弯曲角度β为16.6°、滑雪板夹角λ为37.9°的姿态条件下总升阻比为1.89。在本研究中，在迎风角为30°、滑雪板与身体夹角θ为16°、上半身弯曲角度β为18°、滑雪板夹角λ为40°的姿态条件下总升阻比为1.818。两者的结果非常接近，验证了本研究CFD计算结果的正确性。

从图6~8可以看出，总升力与总阻力、阻力系数与升力系数随滑雪板夹角增大变化趋势一致。同时，图10显示出总升阻比随滑雪板夹角变化基本保持不变，总体呈略微下降趋势，也进一步说明总升力和总阻力变化趋势的一致性。因此，可以认为，滑雪板夹角变化对运动员/滑雪板整体系统升阻比影响很小，但对阻力系数与升力系数有一定影响。

图13 流场形态示意图

Figure 13. Flow Field Form

注：左图为后视图，右图为侧视图。

Nørstrud等[14]通过数值计算研究认为，V型飞行方式代表了更为先进的空气动力，滑雪板在产生良好的升力方面起着重要作用。从表2、图6和图7可以看出，不仅滑雪板升力一直占据总升力63%以上，而且滑雪板阻力也一直占据总阻力65%以上，可以认为，滑雪板气动特性在运动员/滑雪板整体系统中起着更为重要作用，滑雪板气动特性的改善将会获得更为有利的效果，在分析飞行阶段姿态气动特性时，不仅要关注运动员身体姿态，而且应更加关注滑雪板姿态。

另外，图6展示了滑雪板升力随滑雪板夹角增大呈现单调递增的趋势，同时，图8显示了在滑雪板夹角大于28°后升力系数总体呈增大趋势，即增大夹角能够提高总气动升力系数。同时，总力矩大小和滑雪板力矩大小随滑雪板夹角变化趋势一致，而且滑雪板力矩值是总力矩值的1.17倍以上，如图9和表2所示。当夹角大于28°时，随着夹角增大，总力矩值和滑雪板力矩值越大，产生向前倾的效果越明显，可能会对运动员的稳定飞行越不利。本研究结果与Virmavirta[22]的风洞试验研究结论一致。他们重点研究了单个滑雪板的空气动力特性，结论认为，大的滑雪板夹角改善了气动升力系数，但是，张开如此宽度的滑雪板夹角的飞行姿态可能会使运动员飞行变得不稳定。因此，运动员应根据自身技术特点以及训练效果来选择滑雪板夹角，切忌一味为了改善气动升力系数而选择大的滑雪板夹角。总而言之，滑雪板力矩在总力矩中始终占据主导地位，选取合适的滑雪板夹角对飞行稳定性至关重要，优选的滑雪板夹角范围为24°~32°。

随着滑雪板夹角变化，滑雪板背面下半部分压力变化比较明显，同时滑雪板正面压力基本不变且滑雪板背面上半部分的压力变化也比较细微（图11、12），这也是导致滑雪板升力、阻力以及力矩变化的主要原因。当夹角为28°时，滑雪板背面下半部分的次高负压区域明显偏少，低负压区域明显偏多，尤其在滑雪板底端部位，故此时滑雪板正面背面压差偏小，从而滑雪板升力、阻力以及向前倾的力矩值偏小，尤其是力矩值，这也从表2以及图6~9中不难看出。

运动员身后以及滑雪板后侧的流场形态主要以回流涡形式出现，回流涡结构会使能量耗散速度加快。如图13所示，滑雪板后侧回流涡结构明显比运动员身后复杂得多，而且综合尺度及强度也明显大得多，说明滑雪板背面能量损失更大，导致滑雪板的升力和阻力数值较大，并且在总升力和总阻力中占据较大的比重，从而进一步验证了滑雪板气动特性在运动员/滑雪板整体系统中的确起着更为重要作用。同时，对于运动员来说，当夹角为24°时运动员身后回流涡结构尺度以及流动分离程度明显偏大，即此时运动员的升力与阻力偏大；当夹角为28°时运动员身后回流涡结构尺度以及流动分离程度明显最小，即此时运动员的升力与阻力最小，当夹角大于28°时运动员身后回流涡结构尺度以及流动分离程度逐渐变大，直至夹角为40°时运动员身后回流涡结构尺度以及流动分离程度又略微变小一些，即运动员的升力与阻力先变大后略微变小。从表2以及图6~9中不难看出，运动员的升力和阻力随滑雪板夹角变化趋势也与上述变化趋势一致，这两种结果之间也起到良好的相互验证效果。这些研究结果表明，滑雪板夹角变化对运动员气动特性产生一定影响，运动员的升力以及阻力的变化趋势与总升力以及总阻力变化趋势一致。

5 结论

1.滑雪板夹角变化对运动员/滑雪板整体系统的升阻比影响很小，但对总升力、总阻力、升力系数以及阻力系数均产生一定影响，同时对运动员本身的气动特性也产生一定影响。总升力和总阻力随滑雪板夹角的变化趋势与运动员的升力和阻力变化趋势一致。

2.滑雪板气动特性在运动员/滑雪板整体系统中起着更为重要作用，滑雪板气动特性的改善将会获得更为有利的效果，在分析飞行阶段姿态气动特性时，不仅要关注运动员身体姿态，更加要关注滑雪板姿态。

3.总力矩大小和滑雪板力矩大小随滑雪板夹角变化趋势一致，而且滑雪板力矩在总力矩中始终占据主导地位，选取合适的滑雪板夹角对飞行阶段稳定性至关重要，运动员应根据自身技术特点以及训练效果来选择滑雪板夹角，切记一味为了改善气动升力系数而选择大的滑雪板夹角，建议优选的滑雪板夹角范围为24°~32°。

[1] GARDAN N, SCHNEIDER A, POLIDORI G,. Numerical investigation of the early flight phase in ski-jumping[J]. J Biomech, 2017, 59(1): 29-34.

[2] JUNG A, STAAT M, MULLER W. Flight style optimization in ski jumping on normal, large, and ski flying hills[J]. J Biomech, 2014, 47(3): 716-722.

[3] KEIZO Y, MAKOTO T, JUN I,. Effect of posture on the aerodynamic characteristics during take-off in ski jumping [J]. J Biomech, 2016, 49(15): 3688-3696.

[4] LEE K D, PARK M J, KIM K Y. Optimization of ski jumper’s posture considering lift-to-drag ratio and stability[J]. J Biomech, 2012, 45(12): 2125–2132.

[5] MARQUES-BRUNA P, GRIMSHAW P. Mechanics of flight in ski jumping: aero-dynamic stability in pitch[J]. Sports Technol, 2009, 2(1–2): 24–31.

[6] MARQUES-BRUNA P, GRIMSHAW P. Mechanics of flight in ski jumping: aero-dynamic stability in roll and yaw[J]. Sports Technol, 2009, 2(3-4): 111–120.

[7] MEILE W, REISENBERGER E, MAYER M,. Aerodynam-ics of ski jumping: experiments and CFD simulations[J]. Exp Fluids, 2006, 41(6): 949–964.

[8] MULLER W.Performance factors in ski jumping[J]. J Biomech, 2006, 39(1): 192–213.

[9] MULLER W, GROSCHL W, MULLER R,. Underweight in ski jumping: The solution of the problem[J]. Int J Sports Med, 2006, 27(11): 926-934.

[10] MULLER W, PLATZER D, SCHMOLZER B. Dynamics of human flight on skis: improvements in safety and fairness in ski jumping[J]. J Biomech, 1996, 29(8): 1061–1068 .

[11] MULLER W, PLATZER D, SCHMOLZER B. Scientific approach to ski safety[J]. Nature, 1995, 375(6531): 455-466.

[12] MURAKAMI M, IWASE M, SEO K,.High-speed video image analysis of ski jumping flight posture[J]. Sports Eng, 2014, 17(4): 217–225.

[13] MURAKAMI M, IWASE M, SEO K,. Ski jumping flight skill analysis based on high-speed video image[J]. Procedia Eng, 2010, 2(2): 2381–2386.

[14] NØRSTRUD H, ØYE I J. On CFD simulation of ski jumping[M]//Computational Fluid Dynamics for Sport Simulation, 2009, 63–82.

[15] RYU M, CHO L, CHO J. Aerodynamic analysis on postures of ski jumpers during flight using computational fluid dynamics[J]. TJp Soc Aeronaut S, 2015, 58(4): 204–212.

[16] SCHWAMEDER H. Biomechanics research in ski jumping: 1991–2006[J]. Sport Biomech, 2008, 7(1): 114–136.

[17] SCHMOLZER B, MULLER W. Individual flight styles in ski jumping: results obtained during Olympic games competitions[J]. J Biomech, 2005, 38(5): 1055–1065.

[18] SCHMOLZER B, MULLER W. The importance of being light: aerodynamic forces and weight in ski jumping[J]. J Biomech, 2002, 35(8): 1059–1069.

[19] SEO K, MURAKAMI M, YOSHIDA K. Optimal flight technique for V-style ski jumping[J]. Sports Eng, 2004, 7(2): 97–104.

[20] SEO K, WATANABE I, MURAKAMI M. Aerodynamic force data for a V-style ski jumping flight[J]. Sports Eng, 2004, 7(1): 31–39.

[21] VIRMAVIRTA M, ISOLEHTO J, KOMI P,. Characteristics of the early flight phase in the Olympic ski jumping competition[J]. J Biomech, 2005, 38(11): 2157–2163.

[22] VIRMAVIRTA M, KIVEKAS J. Aerodynamics of isolated ski jumping ski[C]. XXV ISB Congress, Glasgow, 2015: 215-223.

Effect of the Ski Opening Angle on the Aerodynamic Characteristics during Flight in Ski-jumping

HU Qi1, CHEN Qi1, ZHANG Wen-yi2

1. China Institute of Sport Science, Beijing 100061, China; 2. Beijing Sport University, Beijing 100084, China.

Objective: This study aimed to investigate the effects of the ski opening angle on aerodynamic characteristics during the flight in ski-jumping. Methods: Refined 3D geometric models and mesh models were established, and aerodynamic characteristics were numerically simulated by using computational fluid dynamics (CFD) with partially averaged Navier-Stokes (PANS) turbulence model. The force and moment, pressure distribution and flow field form of different ski opening angles (24°, 28°, 32°, 36° and 40°) were obtained. Results: 1) As ski opening angle increases ,the total lift force and that drag force, the coefficients of lift and drag, the total torque and the skis’ torque all decrease firstly, then increase, and finally decrease slightly, but the total lift-to-drag ratio almost remains unchanged, and shows a slight downward trend as a whole. 2) The skis’ lift force increases monotonously with the increase of ski opening angle, while the skis’ drag force decreases firstly and then increases. 3) The front pressure distribution of skis is approximately the same and fairly uniform, but the back pressures distribution of the lower part of skis varies obviously with ski opening angle. 4) The flow field form behind athlete and skis mainly appears in the form of reflux vortex. The vortex structure behind skis is much more complicated than that behind the athlete, and the vortex intensity is also much greater. Conclusion: 1) The ski opening angle has little effect on the total lift-to-drag ratio, but has some influence on the total lift and total drag and the coefficients of lift and drag, as well as on the aerodynamic characteristics of the athlete. 2) The aerodynamic characteristics of skis play a more important role in the whole athlete/skis system, so more attention should be paid to skis’ attitude while paying attention to athletes' body posture. 3) The variation trend of total torque and skis’ torque with ski opening angle is consistent, and skis’ torque has always been dominant in the total torque, so it is very important to select the proper ski opening angle for the stability of flight phase, and it is suggested that the optimum range of ski opening angle is 24°~32°.

1000-677X(2018)07-0042-08

10.16469/j.css.201807017

G804.6

A

2018-06-09；

2018-07-12

国家体育总局体育科学研究所基本科研业务费资助项目(18-29)、中央高校基本科研业务费专项资金资助课题(2018RC016)。

胡齐,男,助理研究员,硕士,主要研究方向为体育工程、流体与机械工程、运动生物力学,E-mail:huqi@ciss.cn; 陈骐,男,副研究员,学士,主要研究方向为体育工程,E-mail:chenqi@ciss.cn; 张文毅,女,助理研究员,硕士,主要研究方向为运动生物力学、高等教育管理, E-mail: zhangwy1228@126.com。