基于SVM-CSO算法的PMSM齿槽转矩优化
2018-08-01,,,
,,,
(广东工业大学,广东广州 510006)
0 引言
随着永磁材料性能的不断提高,永磁电机的应用越来越广泛。永磁体与电枢铁心相互作用产生的齿槽转矩是永磁电机固有问题,始终无法避免。齿槽转矩会引起转矩波动,进而导致电机振动和噪声,影响控制系统的精度[1]。
一定程度的永磁体削角既能降低齿槽转矩与谐波畸变率,又能够节省永磁体材料,降低成本。文献[2]利用Maxwell 2D对一款无刷直流电动机在永磁体不同削角的情况进行对比与分析,找出最佳削角。文献[3]针对表贴式永磁同步电机齿槽转矩削弱问题,提出了削角长度比例系数的最佳确定方法。文献[4]对不同程度削角磁极对应的齿槽转矩进行计算,找到最佳削角位置。文献[5]推导无槽口电机的削角永磁体齿槽转矩的解析表达式,并分析了削角对气隙磁场畸变率的影响。
由于解析法的局限性,文献[4]很难准确计算永磁体削角后的齿槽转矩大小。文献[2]选取24组永磁体削角尺寸进行分析,最终找到的削角位置只是局部优点。本文对比分析25组永磁体削角的情况,并在此基础上利用支持向量机进行数据拟合,获得齿槽转矩目标函数,然后通过纵横交叉算法求解确定永磁体的最佳削角方式。Maxwell 2D仿真分析结果显示,本方法是合理有效的,为PMSM磁极削角降低齿槽转矩提供了一种新思路。
1 齿槽转矩解析分析
齿槽转矩是由电枢齿和永磁体之间相互作用力的切向分量引起的转矩,可表示为不通电情况下,电机磁场能量W对定转子相对位置角α的负导数。
(1)
根据电枢铁心导磁率为无穷大的假设,可以得出电机内存储磁场能量的近似表达式
(2)
式中,Wairgap—气隙磁场能量;WPM—永磁体存储的磁场能量;μ0—真空磁导率。
电机的气隙磁密沿电枢表面有规律分布,可表示为
(3)
利用式(3)整理式(2)可得
(4)
式中,δ(θ,α)、hm(θ)—为有效气隙长度、沿圆周方向分布的永磁体充磁方向长度和永磁体剩磁。
根据Br(θ)沿圆周的分布情况,对Br2(θ)进行傅里叶分解可得
(5)
(6)
综合以上各式,并利用三角函数满足的积分关系式,得到不考虑斜槽时的齿槽转矩表达式为
(7)

2 永磁体削角设计
2.1 表贴式永磁电机主要技术参数
本文研究对象的主要技术参数见表1。

表1 主要技术参数
2.2 永磁体不同削角分析
本文以永磁体厚度为6mm,宽度为12mm,结构为面包状,径向充磁的12槽10极表贴式永磁同步电机为例进行分析。提出永磁体削角方式见图1,具有两个自由度,通过改变永磁体边缘a、b的值,即可得到不同程度的削角永磁体。
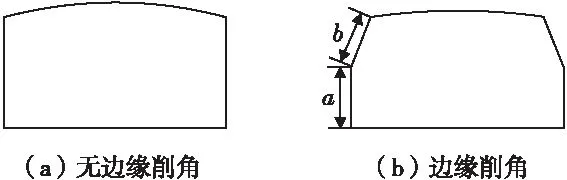
图1 永磁体的削角方式
永磁体削角后的结构如图2所示。

图2 永磁体削角电机结构图
根据上述削角方式,按照不同的a、b值对永磁体进行边缘削角,这里初步选取25组尺寸配合,在Ansys Maxwell 2D中进行仿真分析得到对应齿槽转矩的值见表2。这里的仿真时间设置为6s,即1个周波。
3 削角尺寸优化
齿槽转矩与电机参数之间是高度非线性的,难以建立准确的数学关系式。这里选取永磁体边缘尺寸a、b为设计变量,以齿槽转矩为目标函数进行优化。本文先采用支持向量机回归算法对目标函数建模,然后通过纵横交叉算法对其进行寻优。
3.1 支持向量机回归
支持向量机(Support Vector Machine,SVM)是统计理论的核心,主要用于解决二值分类问题。SVM在机器学习方面性能优良,其应用已拓展至一类分类问题、多类分类问题及回归问题。 通过引入核函数,SVM能降低高维问题的维度,并能更好的求解非线性问题。作为统计学习理论中5种常用核函数之一,高斯径向基核函数目前是SVM的常用选择。
给定n组样本数据{xk,yk},k=1,2,Λ,n,通过非线性映射将数据x映射到高维特征空间G,并在G内执行线性逼近操作。对于上述训练集{xk,yk},基于结构风险最小化原则并使用核函数来求解凸二次规划,进而获得支持向量机模型[6]。
(8)
式中,l—支持向量的数量;αi—拉格朗日常数;k(xi,x)—核函数;b—阈值。
取25组尺寸配合中的20组对SVM算法进行训练,再利用剩下的5组对SVM的拟合效果进行验证。实际值与预测值的对比情况见图3。
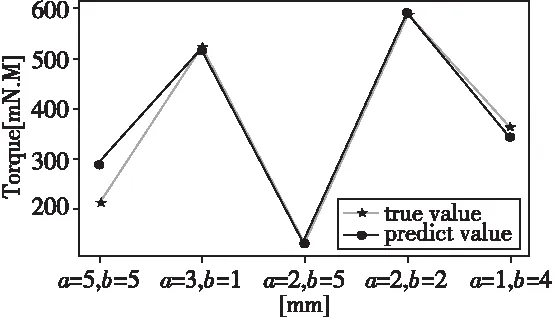
图3 实际值与预测值对比图
由上图可以看出,SVM回归模型对目标函数的拟合效果较好,可用作CSO算法的适应度函数。
3.2 CSO算法寻优
纵横交叉算法(crisscross optimization algorithm,CSO)是一种基于种群的随机搜索算法[7],纵横交叉在每次种群进化迭代中分别在横向和纵向产生中庸解,两种算子交替进行,同时在每次交叉运算后引入竞争操作,保留最优的个体粒子进入下次迭代。CSO的搜索行为由横向交叉算子、纵向交叉算子和竞争算子一起构成。
两个不同个体粒子在所有维之间进行的一种算数交叉称为横向交叉,假设父代个体粒子X(i)和X(j)的第d维进行横向交叉,则产生的子代使用以下公式

式中,d∈(1,D),r1,r2—(0,1)之间的随机数;c1,c2—(-1,1)之间的随机数;X(i,d),X(j,d)—父代种群中个体粒子X(i)和X(j)的第d维;MShc(i,d),MShc(j,d)—通过横向交叉产生的第d维子代。
所有个体粒子在两个不同维之间进行的一种算数交叉称为纵向交叉;假设种群的第d1维和第d2维参与纵向交叉操作,则由以下公式可得到个体粒子X(i)的第d1维和第d2维通过纵向交叉产生的第d1维后代,表示为MSvc(i,d1)
MSvc(i,d1)=r×X(i,d1)+(1-r)X(i,d2)
(10)
式中,d1,d2∈N(1,D),i∈N(1,M),r∈U(0,1)
文中CSO算法以削角尺寸a、b为优化变量,SVM回归模型为目标函数,其具体参数设定为:种群数量30,最大进化代数100,纵向交叉率0.8。优化结果如图4所示,最佳削角尺寸为a=3.8477,b=4.3537,对应的Torque=115.29m N·M。

图4 CSO算法寻优结果
3.3 仿真验证
将SVM-CSO算法优化过的削角尺寸a=3.8477,b=4.3537代入Maxwell 2D仿真,结果见图5,经过优化后的齿槽转矩为115.62mN.M,与算法求解值115.29接近。同时与表2的结果对比,验证了本方法的准确性。
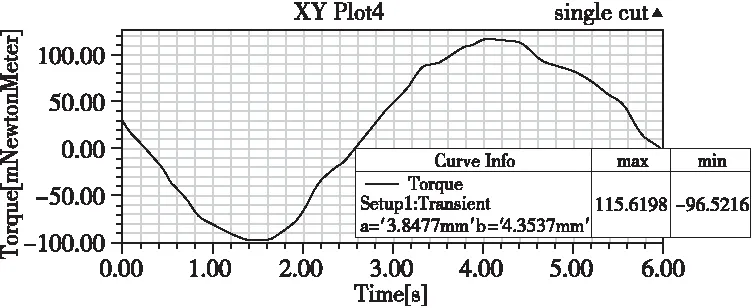
图5 优化后PMSM齿槽转矩
4 结语
本文以12槽10极表贴式永磁同步电机为例,使用Ansys软件对永磁体不同位置削角时的齿槽转矩进行仿真分析。以25组数据为样本空间,通过支持向量机算法建立目标函数,并使用纵横交叉算法求解获得最优的削角尺寸,最后应用有限元仿真软件验证。研究结果表明SVM-CSO算法模型的有效性及准确性,为电机结构参数优化提供了新思路。
