搅拌介质磨机湿法制备荷叶粉及其动力学研究

俞建峰赵 江楼 琦梁 洁王 立

(1. 江南大学机械工程学院，江苏 无锡 214122；2. 江苏省食品先进制造装备技术重点实验室，江苏 无锡 214122；3. 江南大学食品学院，江苏 无锡 214122)

荷叶(Lotus leaf)是睡莲科植物莲的新鲜或干燥叶片[1]，是一种常见的药食两用药材。荷叶在亚洲有着悠久的种植和应用历史[2]。中国荷叶资源丰富，但加工方法落后[3]，利用率不到荷叶总产量的1%。荷叶的主要活性成分为黄酮类[4]和生物碱类[5]。这些物质能够保护机体组织不受氧化性物质侵袭的伤害[6]。此外荷叶中还含有β-胡萝卜素、VC、酒石酸、枸橼酸、苹果酸、草酸等物质[7]。

搅拌介质磨机(又称砂磨机)具有研磨效率及能量利用率高的优点，被广泛应用在涂料[8]、制药[9]、冶金[10]和选矿[11]等行业。植物组织的破碎是植物有效成分提取工艺中的关键技术之一。物料经超细粉碎后，其物理和化学特性会发生较大变化，从而大幅度提高有效成分的提取率。Gábor等[12]使用搅拌介质磨机研磨葡萄籽，研究了应力强度和应力次数对葡萄籽粉体粒度分布的影响，确定了最佳研磨条件为应力数297，应力强度4.81×10-4N·m，研磨前后材料的化学结构没有显著变化，证实了葡萄籽微粉化有利于有效成分提取。Ullah等[13]使用搅拌介质磨机湿法研磨豆渣中不溶性膳食纤维(IDF)，分析了不溶性膳食纤维的结构特征和物理化学性质的变化。在研磨6 h后，IDF的粒径从66.7 μm 减小到544.3 nm，最终产品的溶胀力、水溶性指数和表观黏度显著增加。

目前应用湿法搅拌研磨制备超细荷叶粉的研究尚属空白，也没有相应的工艺参数可以参考。针对这一情况，本研究利用搅拌介质磨机进行湿法研磨制备荷叶粉的试验，研究不同搅拌转速对研磨速率的影响，并通过CFD-DEM耦合仿真研究不同转速下搅拌介质磨机中流场运动规律特性和研磨介质平均碰撞能变化，旨在为深入研究荷叶粉湿法研磨工艺提供参考。

1 材料与方法

1.1 材料与仪器

新鲜荷叶：采摘于无锡江南大学校园，热风恒温60 ℃干燥12 h，备用；

氧化锆球：φ=1 mm，宜兴市鼎信涂料机械经营部；

激光衍射粒度分析仪：Mastersizer2000型，英国马尔文仪器有限公司；

恒温鼓风烘干干燥箱：DHG-9076A型，上海精宏实验设备有限公司；

多功能食品料理机：AQ-180B型，慈溪市耐欧电器有限公司；

卧式介质磨机：PHN-0.5CA型，广州派勒纳米科技有限公司；

蠕动泵：BT100-2J型，保定兰格恒流泵有限公司。

1.2 试验方法

将干燥后的荷叶经多功能食品料理机粗粉碎后，加入搅拌介质磨机配套的分散罐中。研磨腔中加入40%的1 mm氧化锆珠，搅拌介质磨机在搅拌转速为500，1 000，1 500，2 000，2 500，3 000 r/min的条件下研磨荷叶粉30 min，每隔5 min从循环出口处抽取样品进行粒度分析。

1.3 研磨动力学理论

研磨动力学主要关注粉体粒径随时间的变化情况。Epstein[14]提出的研磨过程解析模型主要包括两部分：① 破碎速率函数(选择函数)；② 破碎分布函数。破碎速率函数Si是第i级粒径被选择破碎的概率，破碎分布函数Bij表示第j级粒径的颗粒在研磨后进入第i级粒径的质量分数。在连续粉碎过程中，可以用累积粒径分布来描述粉碎过程：

(1)

式中：

t——研磨时间，min；

Si——第i粒级的破碎速率函数，min-1；

wi(t)——第i级粒径的质量分数；

Kapur等[15]对研磨过程解析模型进行近似求解，获得研磨过程动力学方程：

(2)

式中：

Ri(0) ——第i粒级的0时刻的累积筛余分数，%；

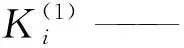
采用一级Kapur函数可以比较准确地描述搅拌砂磨的粉碎过程[15]，可以比较容易地获得选择函数和分布函数。其主要依据方程为：

(3)

(4)

(5)

2 数值模拟

2.1 模型构建及网格划分

棒销式搅拌介质磨机研磨腔基本结构见图1。研磨腔内壁直径95 mm，长度为100 mm，研磨腔容量为0.5 L，搅拌器转轴转速200～3 000 r/min(可调)。

图1 介质磨机研磨腔

本试验应用Fluent 17.0的前处理软件ICEM来建立搅拌研磨流体计算域网格模型。为了简便运算和节省时间，在三维建模过程中只截取研磨腔一段进行模拟，并且省略了圆角、倒角等细节。为提高计算效率和计算精度，仿真计算中采用结构化网格，共划分139 544个，流体区域结构网格划分见图2。计算区域分为两部分，包含搅拌器在内的旋转区域和静止区域。

图2 流体区域结构化网格划分

2.2 计算流体动力学模型

基于欧拉-拉格朗日方法的CFD-DEM耦合模型对搅拌介质磨机研磨过程进行模拟研究。其基本耦合过程为：首先在EDEM 2.7软件中设置颗粒相关工程参数；然后打开耦合服务，启动Fluent 17.0软件设置流体相关参数；而后打开耦合界面设置耦合路径；最后在Fluent 17.0启动运算服务。其中EDEM仿真时间步长设置为Fluent步长的整数倍。

应用流体力学仿真软件Fluent 17.0进行流场模拟，研磨腔内流体选用水，水是牛顿流体，流场雷诺数Re与流体密度ρ以及流体黏度μ有关，计算公式为：

(6)

式中：

Re——雷诺数，%；

ρ——流体密度，kg/m3；

u——流速，m/s；

d——当量直径，m；

μ——流体黏度，Pa·s。

当量直径取d=0.095 m。u取棒销末端线速度，棒销半径r=0.04 m，经计算工程中的临界雷诺数为Rec=2 300，当雷诺数Re>Rec时，流体运动状态属于湍流。不同转速下的流体运动状态见表1。

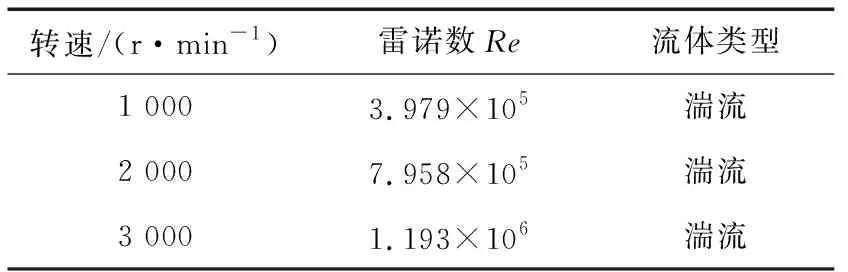
表1 不同转速时流体运动状态

根据流体动力学理论，搅拌介质磨机内部流场满足质量守恒方程(连续性方程)，动量守恒方程(N-S方程)和能量守恒方程。

在Fluent流体仿真中的绝大多数问题都是在静态坐标系下的，而本试验中旋转区域是研究的重点。本试验采用动参考系下滑移网格[16]方法来解决旋转流动问题，滑移网格[17]将计算区域分为两部分，包含搅拌器在内的旋转区域和静止区域。划分网格后定义静止区域与旋转区域的动静耦合交界面(interface)，旋转区域与旋转元件的接触表面为无相对运动。标准的k-ε模型、RNG-k-ε和可实现k-ε模型都可以应用于高雷诺数计算，由于RNG-k-ε在湍动能耗散率计算精度较高，故采用RNG-k-ε湍流计算模型，假设无进出口边界条件，考虑到流体的黏性作用，固壁表面边界条件采用无滑移边界条件。收敛残差值设定为0.001。CFD-DEM耦合迭代计算到收敛，Fluent1 7.0软件后处理得到流场特性云图，分析流场运动的规律。

2.3 离散元模型

应用离散单元法模拟软件EDEM 2.7对搅拌介质磨机研磨介质运动进行仿真，离散单元法基于牛顿运动定律来描述每一个颗粒的运动。EDEM和Fluent模拟中采用同一网格模型。搅拌介质磨机研磨腔体及搅拌器材料为钢，研磨介质材料为氧化锆球。表2为EDEM中物料属性。

表2 颗粒模型的物理属性

EDEM模拟在物理属性中选择颗粒与颗粒、颗粒与几何体的接触模型为Hertz-Mindin(no slip)，即无滑动接触模型。设置Z轴负方向为重力加速度方向。模拟研磨介质氧化锆球直径放大3倍为3 mm[18]，介质填充率为40%，经计算介质球颗粒数为5 100个。设置好全局参数后，利用EDEM软件Simulator模块进行仿真计算。其中，时间步长选为Rayleigh时间步长的35%，网格尺寸设为最小颗粒半径的3倍，数据保存时间间隔为0.1 s。模拟时间为2 s。利用EDEM软件后处理部分对研磨介质质量、研磨介质碰撞总次数、研磨介质相对法向平均速度等数据进行提取。

2.4 流体动力学黏性能量耗散率表征

在不可压缩的各向同性湍流能量流动过程中，黏性能量耗散率P是动力黏度和平均速度梯度的函数[19]。可以用来分析研磨腔中各部分的研磨效果[20]，其定义：

P=μφv，

(7)

式中：

φv——能量耗散函数。

能量耗散函数φv的定义为：

(8)

式中：

u——x方向分速度，m/s；

v——y方向分速度，m/s；

w——z方向分速度，m/s。

在Fluent中不能直接取得黏性能量耗散率P的定义，研究[21-22]认为可以选用剪切率S来替代表征：

(9)

由于水为牛顿流体，动力黏度是一常量，剪切率S与黏性能量耗散率P平方根呈正比，可以用来表征搅拌介质磨机研磨腔局部研磨效果。

3 结果与讨论

3.1 搅拌转速对剪切率分布的影响

通过Fluent 17.0进行研磨腔流体流动规律数值模拟，得到一系列剪切率分布云图，流体力学中剪切率分布可以用来表征黏性能量耗散率函数，进而可以用来研究搅拌介质磨机研磨腔中局部的研磨效率。从图3中可以看出，棒销式搅拌器中心部位剪切率较小，而棒销式搅拌器与研磨腔筒壁之间的区域剪切率较大，特别是棒销末端部位剪切率最大。流体之间的剪切力与速度梯度之间存在正比关系，剪切率大的部位也是流体速度梯度大的部位，速度梯度越大表示研磨介质碰撞越激烈，研磨效果越好。因此搅拌介质磨机研磨腔的有效研磨区域是在搅拌器外侧到筒壁之间和搅拌器内壁附近。

图3 不同转速下剪切率分布

观察不同转速(1 000～3 000 r/min)下的剪切率云图，随着搅拌转速增大，研磨区域明显扩大，荷叶粉被捕捉破碎的概率增大，研磨效果加强。但是较大转速的能量耗散也在增加，能量利用效率反而降低。并且较大转速下，研磨介质对搅拌器和筒壁冲击碰撞加剧，设备磨损增加。因此，合理选择搅拌器转速对荷叶粉研磨速率和设备使用寿命至关重要。

3.2 搅拌转速对荷叶粉粒径的影响

试验中，氧化锆球直径为1 mm，填充率为40%。图4是不同搅拌转速时，荷叶粉中位粒径D50在研磨过程的变化情况。从图4可以看出：在初始阶段荷叶粉中位粒径D50下降较快，20 min后，粒径下降变迟缓。搅拌转速在3 000 r/min时，荷叶粉在20 min内D50从20.946 μm下降到7.720 μm，D90从170.511 μm下降到 41.059 μm，继续研磨到30 min时，D50变为5.856 μm，D90变为35.060 μm。在刚开始阶段，由于荷叶粉粒径较大，被研磨介质碰撞捕捉的几率大，粒径下降速度较快，在达到一定水平后，继续研磨粒径并不会下降甚至因为有团聚现象，粒径会有小幅度上升，最终达到稳定平衡阶段。

搅拌介质磨机是以研磨介质互相碰撞产生冲击和摩擦作用，从而使物料破碎。搅拌转速越高，研磨介质和物料获得的能量越多，研磨介质之间的碰撞与摩擦作用越剧烈。提高搅拌转速可以增大研磨速率，获得更小的粒径。荷叶粉粉体在介质磨机中湿法研磨是颗粒破碎-团聚的过程，研磨到达一定程度后，荷叶粉体粒径并不会继续减小，而是稳定在某一水平。因此，接下来的研磨速率分析中，只关注荷叶粉在20 min之内的研磨破碎情况。

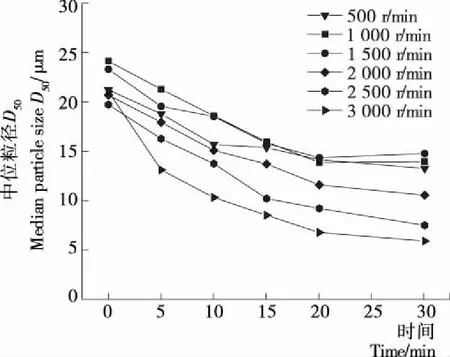
图4 不同转速下中位粒径的变化

3.3 搅拌转速对荷叶粉研磨速率的影响

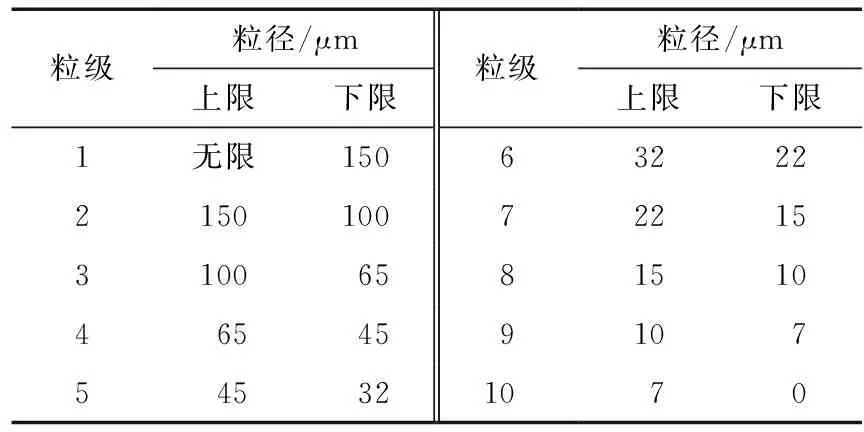
表3 荷叶粉粒级及其上下限

图5是搅拌转速分别为1 000，2 000，3 000 r/min时，根据式(5)对各粒级的累积筛余分数进行的一级Kapur系数线性拟合。由此得出的拟合斜率为此粒径下的Kapur函数，由式(4)可知，Kapur函数绝对值越大，研磨速率Si越大。

图6是搅拌转速分别为1 000，2 000，3 000 r/min时，不同特征粒径下的Kapur函数绝对值变化。由图6可知，在搅拌研磨中，荷叶粉颗粒粒径越大，搅拌介质磨机研磨速率越快，随着粒径的减小，颗粒质量减小，破碎需要的能量比大粒径颗粒高，搅拌介质碰撞的能量不足以使物料破碎，研磨速率降低。并且在每一粒级下，搅拌转速越高，研磨介质获取的动能越高，物料颗粒获得的能量增加，研磨速率也随之增加。

图7是搅拌转速分别在1 000，2 000，3 000 r/min时，荷叶粉研磨20 min后得到的第1粒级累积破碎分布函数Bij，破碎函数是用来表征不同破碎模型的特征参数，Menacho[23]研究发现关于Bij=f(xi/xj)的方程曲线可以用来确定研磨过程中的不同破碎方式。通过与方程曲线比较，可以发现在荷叶粉湿法研磨过程中，破碎方式不是单一的，而是冲击破碎和摩擦破碎并存。搅拌转速越高，冲击粉碎的作用越显著。在搅拌转速较低时，研磨介质获得的能量较低，介质碰撞能量不足以满足物料的破碎，因而更多地是以摩擦来粉碎，由于荷叶粉的物料特性，摩擦破碎方式要比冲击破碎方式的研磨效率更低。增加搅拌转速可以加强研磨效率。

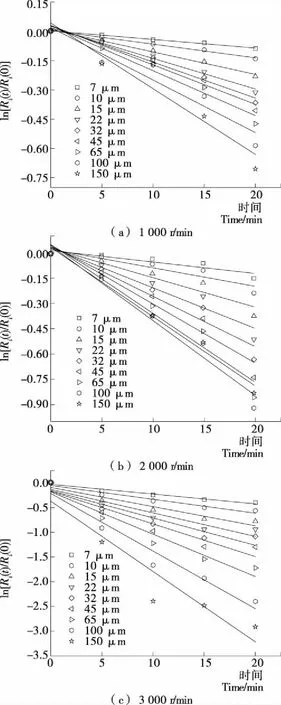
图5 不同搅拌转速的一级Kapur系数线性拟合

Figure 5 Calculating Kapur function by linear data fitting of residual fraction with different stirring speeds

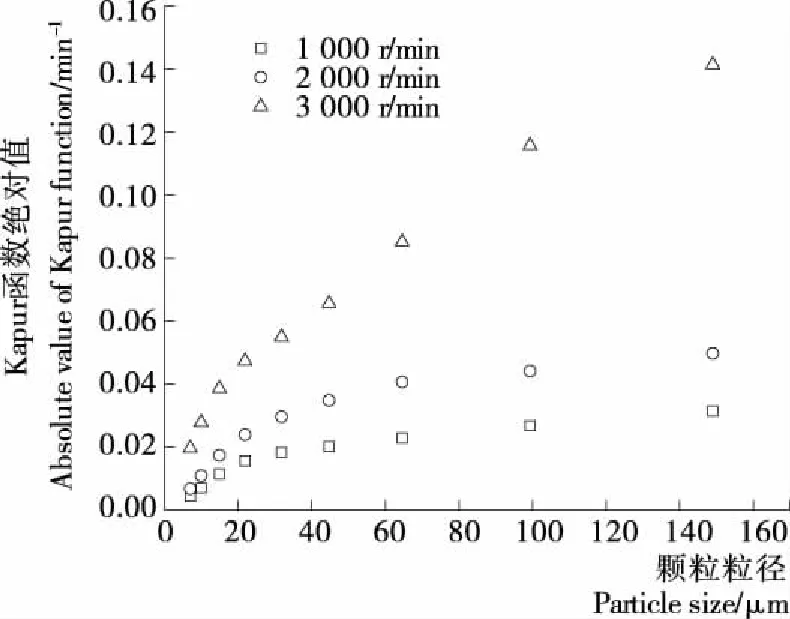
图6 不同搅拌转速的Kapur函数绝对值

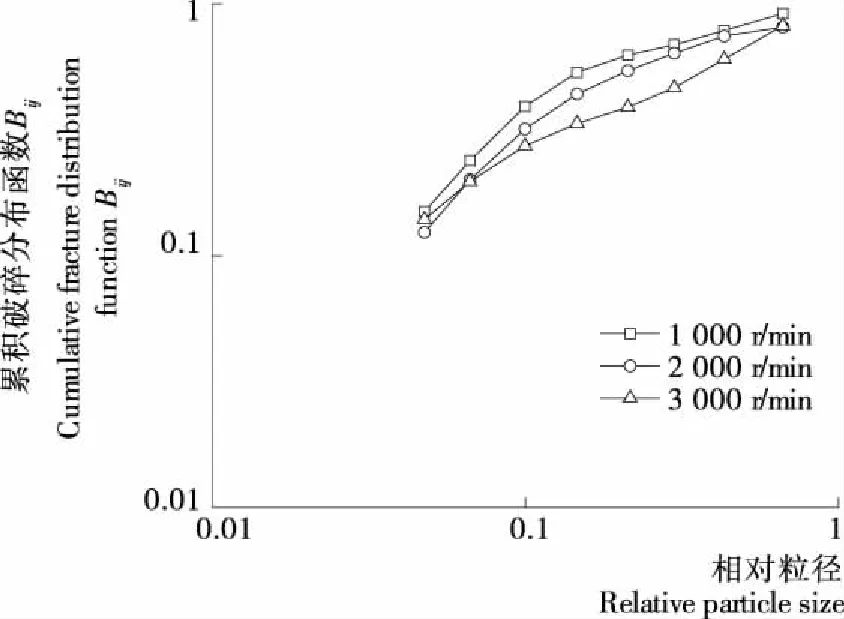
图7 不同搅拌转速下的第1粒级的Bij=f(xi/xj)曲线

3.4 搅拌转速对研磨介质碰撞能量的影响

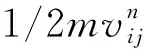
从图8中可以看出，研磨介质平均碰撞能量与研磨速率存在一次线性关系，随着研磨介质碰撞能量的增加，研磨速率增加。表4为研磨介质平均碰撞能量与研磨速率线性关系的拟合结果。结果表明：研磨介质平均碰撞能量与研磨速率之间存在稳定相关性，证实了数值仿真模型的有效性。仿真模拟的结果可以对荷叶粉研磨速率进行预测。

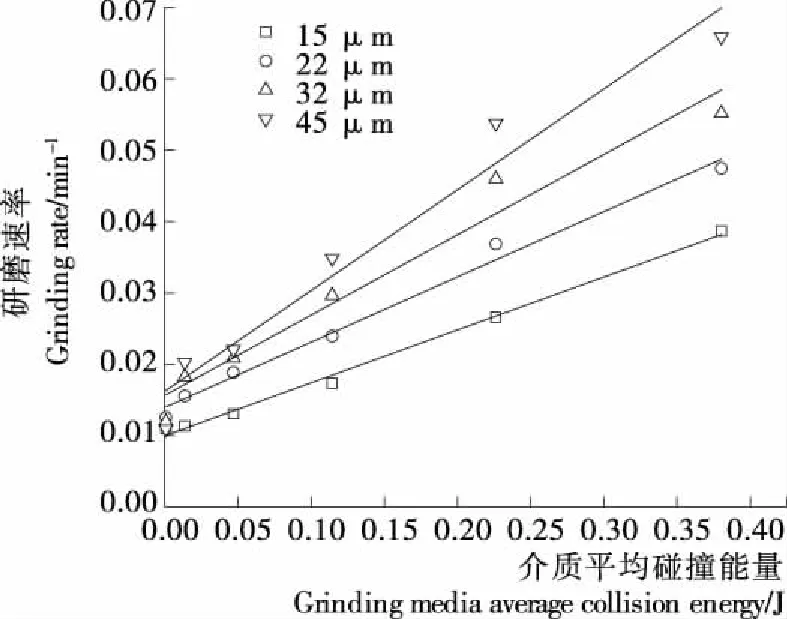
图8 研磨介质碰撞能量与研磨速率关系

Figure 8 Relation between average collision energy of grinding medium and grinding rate

表4 研磨速率与介质能平均碰撞能量拟合结果

4 结论

荷叶粉湿法搅拌研磨过程符合一级研磨动力学方程，研磨过程中，随着荷叶粉粒径由大变小，荷叶粉研磨速率也随之减小。研磨过程中存在冲击破碎与摩擦破碎2种破碎方式。提高搅拌转速，冲击破碎方式更加显著，荷叶粉颗粒获得能量增加，荷叶粉研磨速率也会随之增加。研磨介质平均碰撞能量与不同粒级研磨速率之间存在线性关系。提高搅拌转速，荷叶粉各粒级的研磨速率也会随之增加。模拟仿真结果可以应用于对荷叶粉研磨速率的预测。影响荷叶粉研磨速率的因素还有研磨介质颗粒大小，研磨介质填充率以及荷叶粉初始粒径等，相关内容有待进一步深入研究。