塔里木盆地顺托果勒地区志留系柯坪塔格组米兰科维奇旋回沉积记录

贾东力，田景春，林小兵，杨国华，冯文新，张 翔，唐 艳，杨辰雨

(1.成都理工大学 沉积地质研究院，四川 成都 610059； 2.郑州工业贸易学校，河南 郑州 450007；3.四川省第三测绘工程院，四川 成都 610500；4.四川省地质矿产勘查开发局，四川 德阳 618000)

旋回地层特指建立在时间、尺度及成因共同约束下，顶底由层序界面限定和内部相对整合的具有旋回特征的沉积地层，主要研究记录并保存在地层中的米氏旋回，即由地球天文轨道周期变化形成的沉积旋回记录[1-2]。而轨道参数的周期变化引起了地球表面日照量的周期性变化，进而导致全球气候的周期性变化，并被记录在对气候变化响应相对较敏感的沉积体系中。这些由地球天文轨道驱动力造成的旋回地层记录被称为米兰科维奇旋回，即天文旋回理论[3]。

前人研究表明，米兰科维奇旋回作为一种轨道力存在于太古宙以来的各个地史时期。其地球轨道偏心率、斜率和岁差三要素的周期性变化对地表日照量、全球气候和海平面变化具有明显的影响，结果导致天文轨道驱动着海平面的变化，从而控制着三级、四级、五级甚至六级沉积层序。笔者正是在本文中考虑到米兰科维奇旋回中3个周期之间的比率关系在地质历史时期具有相对的稳定性[1,4]，如果能够在地层所包含的各种旋回中找到与米氏周期比率相等或相近(误差在5%以内)的关系，我们就认为研究层段的各旋回对应于各米氏旋回，从而就完成了“深度域”和“时间域”之间的数据转换，最后通过计数法得到目的层段内所包含米氏旋回的个数，进而就可以得到分析层段的持续时间[5]。因此米兰科维奇旋回特征及高频层序研究能够用于分析古环境和古气候变化、计算目的层位的沉积速率、区域地层等时精细对比以及完善地层年代表等研究，为理解和解决地球科学领域的众多问题提供依据。

本文针对塔里木盆地顺托果勒低隆起以海相碎屑岩沉积为主的柯坪塔格组为对象，运用频谱分析法，EMD(经验模态分解法)法及Fischer图解法对柯坪塔格组进行米兰科维奇旋回分析，建立柯坪塔格组“浮动”天文年代标尺，以短偏心率周期125Ka为划分标准，建立高精度层序地层格架，分析各高频旋回叠置关系及差异性，旨在把米兰科维奇旋回理论应用在高频层序划分过程中，同时为本地区及类似地区提供一种分析层段持续时间，沉积速率及高频旋回地层划分的显著方法。

1 地质背景

现今塔里木盆地是古生代克拉通盆地与中新生代前陆盆地叠置复合而形成的大型多期叠合盆地，在地貌上被天山造山带、西昆仑造山带和阿尔金造山带所围限，其古生代的构造格局，以发育多个大型的北西西向、北东东或北东向的古隆起、古坳陷带为显著特征，也发育了从海相、海陆过渡相、陆相的完整海侵-海退沉积旋回[6]。本文的研究区顺托果勒低隆区，南北方向处于塔北隆起和塔中-古城隆起的夹持之间，东西方向上处于阿瓦提凹陷与满加尔坳陷之间的低梁部位，呈“马鞍形”处于南北两个正向构造带和东西两个负向构造带之间(图1)[7]。自奥陶系以来，顺托果勒隆起及邻区经历了碳酸盐岩台地发育、台地内隆起—斜坡形成、北西向与北东向断裂改造，岩浆活动、区域翘倾变动及早期断层再活动等多个阶段[8]，在早、中奥陶世处于稳定的克拉通沉积环境，在晚奥陶世，塔中地区发生台盆分异，卡塔克隆起发生隆升，而处于围斜区的顺托果勒地区稳定沉降，早志留世，卡塔克隆起未受到明显的构造活动影响，顺托果勒地区持续稳定沉降，故志留系保存了较完整的古生代地层。

2 地层划分

区内志留系柯坪塔格组发育较为完整，普遍埋深大于5 100 m，其作为1个二级层序的底界，代表盆内重要构造运动的界面(晚奥陶世末构造运动)，强烈的构造活动造成盆地内地层大规模的隆升，变形及后期的剥蚀改造，形成盆内广泛分布的不整合，同时剥蚀强度的差异也造成了志留系柯坪塔格组沉积层序具有不对称的结构特点[9]。沉积充填序列上，柯坪塔格组具有明显的3个岩性段，自下而上分为下砂岩段(S1k1)，中泥岩段(S1k2)，上砂岩段(S1k3)。其中上段沉积了一套海相细砂岩、中砂岩、粉砂岩、粉砂质泥岩互层，中段沉积一套绿色、灰绿色泥岩，下段为一套砂岩与泥岩互层组合(图2)。结合前人研究和岩心观察可明显看出顺托果勒地区柯坪塔格组属滨岸和潮坪环境沉积产物[10-12]。由于在滨岸和潮坪沉积环境中受波浪及潮汐作用影响，沉积作用变化较活跃，可容纳空间变化成为旋回地层沉积厚度的最主要控制因素，同时该地层保存较多，较完整，岩性和沉积构造清楚，因而柯坪塔格组是进行旋回地层分析的良好地层。

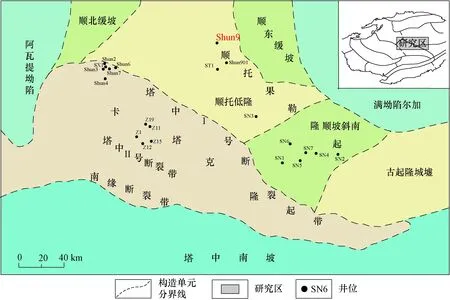
图1 塔里木盆地顺托果勒低隆区构造示意图Fig.1 Structural location of the Shuntuoguole low uplift area,Tarim Basin

3 数据选择及处理

由于气候变化与地球轨道参数两者之间的关系密不可分，故古气候替代指标是能够反映之前气候变化的各类地球化学和地球物理等参数，同时经过前人的研究证明，在深海、湖泊和河流沉积物中均发现了米氏旋回记录[13]，在缺乏准确的地层测年数据下，稳定沉积地层中符合采样密度要求的岩性变化、地球化学数据(如氧同位素δ18O，碳同位素δ13C，87Sr/86Sr比值，CaCO3含量，磷/钛等)、古生物指标(如生物的绝灭速率，生物更替，丰度等)和能反应气候变化的地球物理数据(如自然伽马，磁化率,岩石密度和色率等)[3,14]均可作为替代性指标用于米兰科维奇旋回的研究。

米兰科维奇旋回的周期性(准周期性)变化的最终结果是沉积层序有规律的发育，表现在沉积结构、岩性、岩相呈现出韵律性和旋回性，而在众多替代性指标中，任何反应岩性变化的测井曲线则连续的记录下了这种变化，并且具有很高的纵向分辨率[15]。例如：J.D.Ogg用测井曲线分析沉积速率的不连续，Spaletti等利用AC、RT和GR对阿根廷下白垩地层的研究，Fotini和Maltezzou等对科学深钻测井曲线的分析都证明海相、湖相地层都可用测井曲线分析米兰科维奇周期[16]。

因此在研究过程中，首先是要选择合适的替代性指标来开展旋回地层学研究工作，理论上，每一个测井数据都能体现出岩性变化具有一定的周期性，其中的自然伽马曲线记录了在放射性核衰变过程中发出的伽马射线的强度，其强度与岩层中的40K、232Th及238U的含量有关。粘土物质和有机质对放射性元素具有很强的吸附能力，而且其缓慢的沉积速率让放射性元素有足够的时间从流体中分离出来，因此，自然伽马曲线既能反映岩层中泥岩和有机质含量的变化，同时与控制气候变化的因素具有良好的相关性，故与其他测井曲线相比，自然伽马曲线可以敏感地反映岩性旋回和岩相韵律互层在深度域中的变化。

由此，本文选择了钻遇地层较全的顺9井自然伽马测井曲线进行频谱分析、EMD分解及Fischer图解等处理。为满足分析需要，首先对测井曲线数据去除各种环境“噪音”，包括如下预处理：1)去极值，即去除偏移均值很大的异常值，用均值或插值代替；2)去除线性趋势化，即去除数据序列随时间或深度而逐渐变大或变小的趋势性变化，本次处理选用了5阶去趋势化处理方法；3)小波去噪，即选用小波分析中的dbN小波去除产生干扰的频率成分。

图2 塔里木盆地顺托果勒低隆区志留系地层沉积演化示意图Fig.2 Sedimentary evolution of the Silurian in the Shuntuoguole low uplift area,Tarim Basin

4 旋回地层

4.1 理论轨道周期

米兰科维奇旋回理论认为，地球轨道偏心率、斜率及岁差3个地球轨道运行参数的周期性变化会造成地球接收太阳辐照量的周期变化，必定会导致气候的周期性变化，进而形成沉积环境的周期性变化并在地层沉积过程中被记录下来。经过近半个世纪的科学实践，与米兰科维奇旋回有关的天文模型理论周期已经成为了一个校准地质年代标尺的重要工具[17]。

目前的轨道要素计算方法中，地月系统围绕太阳公转的轨道和地月相互作用对地球轨道的影响被通常作为主要的考虑因素，这其中具有代表性的有Berger、Loutre与Laskar等提出的方案[18]。Laskar等在2004年考虑了地球轨道参数在地月系统绕太阳公转和地月相互作用的影响下均会发生变化，故由太阳系各行星轨道运动方程数值积分计算得出La2004解决方案[19]，随后在2011年Laskar等学者论证了一个具有更高精度的新解决方案——La2010(La2010a-d)[20]。不过值得注意的是，虽然我们采用La2004和La2010a方案分别在42 Ma和60 Ma内能计算出轨道变化周期且具有较高的精度，但在老地层中，由于潮汐耗散、气候摩擦以及太阳系的各行星轨道参数模型无法准确预测等因素，导致上述两种解决方案的斜率和岁差周期随着地质时间的演化而有不同程度的变化。例如，现如今的岁差旋回周期大致为19～23 ka，相较于中泥盆世慢了约3～5 ka。

综上所述，本文在总结了前人研究的基础上，根据卫星测量的地球数据对米兰科维奇的地球轨道参数进行了计算及校正(表1)[18,21-24]，其结果揭示了405,125,95 ka三种稳定的偏心率周期。柯坪塔格组位于志留系下部，根据2016年国际地层年代地层表可知，早志留世柯坪塔格组大致开始于(443.8±1.5) Ma，结束于(433.4±0.8) Ma。鉴于此，本次研究根据Berger提出的计算模型，选择了440 Ma对应的斜率长短周期38.1，31.1 ka和岁差长短周期19.5，16.6 ka作为柯坪塔格组沉积时期的米氏旋回周期进行高频旋回分析[18]，这些理论轨道周期之间的比例关系稳定不变，可作为本次研究中确定天文周期的基准。

4.2 米氏旋回确定

在构造稳定的前提下，地层沉积时期的环境周期性变化可在测井曲线的周期性变化中详细的体现出来，而对测井曲线数据进行频谱分析来进行周期性旋回地层研究已经是一种既成熟又有效的统计分析方法。其实质是将测井曲线看作是各种地质因素共同在深度域(或时间域)上引起地层规律性变化而形成的一个综合信号，通过对目的层段的测井曲线进行频谱分析，计算随深度变化的周期信号的频率，找出这段曲线的主要周期成分，经过反复比较，发现层段范围内波长比率与标准天文周期固定比率相同或相近的频率，两者的比率越接近，越能反应古气候变化信息，进而可揭示该段地层旋回形成过程中主要受到了哪些天文周期的控制，就可认为研究层段的各地层旋回对应于米兰科维奇旋回的各个周期[25]。

本文研究中，利用了PAST软件的REDFIT程序对顺9井自然伽马测井曲线数据进行频谱分析，主要选择90%置信度为计算阀值(表2;图3)。其横坐标为“频率”，由于地层为深度序列，故此处的频率特指单位厚度内地层旋回变化的次数。纵坐标为“能量”，表示各个频率的能量大小和其深度域中的相对重要性大小。能量值越大，地层中出现的对应周期的沉积旋回越频繁，因此频谱曲线能量高点的谐频对应于曲线主频，将其换算为相应波长，再根据数据采样间隔可得出相应旋回厚度。从国际年代地层表(2016版)可知志留系柯坪塔格组沉积大致介于(433.4±0.8)～(443.8±1.5) Ma，故其沉积时限应介于8.1～12.7 Ma。在处于大于90%置信度的主要频率中，假定A点对应长偏心率旋回，即周期为405 ka，其平均沉积旋回厚度则等于16.73 m。由于顺9井柯坪塔格组地层埋深为5 206～5 641 m，即地层厚度为435 m，可计算出柯坪塔格组的沉积时限为10.4 Ma。处于柯坪塔格组沉积时限范围内，假设成立；若远远超出了志留系柯坪塔格组的沉积时限，则假设不成立，该点周期只能与短偏心率旋回或更小的米级旋回对应。同理可判定点A，B，C，D和E对应频率为0.007，0.024，0.032，0.079和0.097，其相对应的平均沉积旋回厚度为16.73，5.24，3.92，1.59和1.26 m，同时之间比例关系为1 ∶0.313 ∶0.234 ∶0.095 ∶0.075,与轨道周期405 ∶125 ∶95 ∶38.1 ∶31.1 ka的比例关系1 ∶0.309 ∶0.234 ∶0.094 ∶0.076异常接近，仅仅在短偏心率和斜率周期产生极小的误差。旋回厚度间的比例关系与理论天文周期比例的差异均在5%以内，而在频谱分析结果中可看到，偏心率周期和斜率周期均处于90%置信度之上，岁差周期在记录中处于90%置信度以下，相对振幅能量偏心率>斜率，表明柯坪塔格组沉积过程中，偏心率影响最大，而岁差受到构造运动和气候周期等的强烈干扰，信息记录能量较弱且不连续，同时部分峰值虽满足沉积时限范围的条件，但未找到与米氏旋回周期相似的比率，说明这些峰值很可能为噪音或者受其他周期旋回共同控制的结果。综合分析认为，志留系柯坪塔格组中很好地保存了米兰科维奇旋回，因此可认为旋回厚度16.73 m对应于405 ka长偏心率周期，5.24和3.92 m分别对应于125 ka和95 ka的偏心率周期，1.59和1.26 m分别对应于38.1 ka和31.1 ka的斜率周期。利用平均旋回厚度除以其对应的天文旋回周期，可得到平均沉积速率，而且不同的旋回厚度所计算得出的沉积速率误差不大。本文计算结果表明柯坪塔格组平均沉积速率约为4.15 cm/ka，与Chen Shuping[26]对塔里木盆地沉积速率的计算结果相符合，间接证明本文的频谱分析结果的正确性。

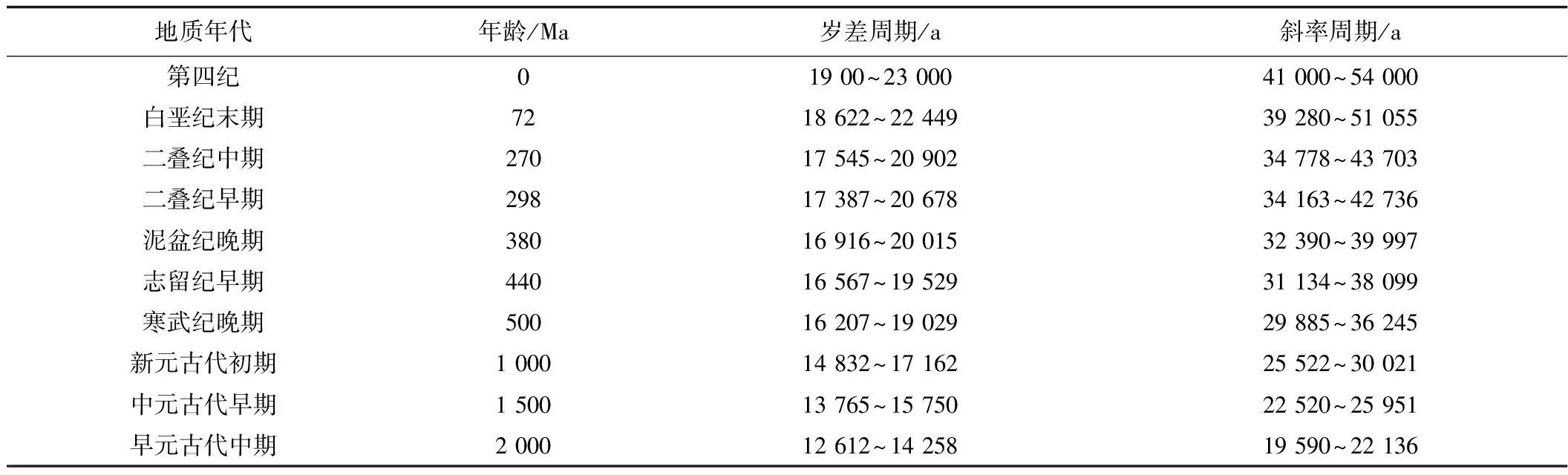
表1 地史时期的岁差和斜率周期Table 1 Precession and obliquity cycle during the geological time

表2 塔里木盆地顺9井柯坪塔格组频谱分析相关参数Table 2 Parameters for spectral analysis of the Kepingtage Formation in Well Shun-9,Tarim Basin

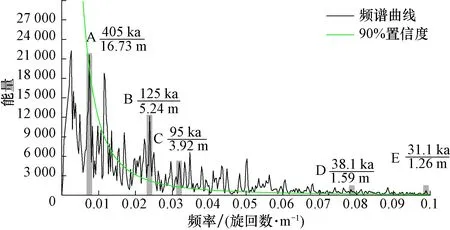
图3 塔里木盆地顺9井柯坪塔格组自然伽马曲线频谱分析Fig.3 Spectral analysis of natural gamma logs of the Kepingtage Formation in Well Shun-9,Tarim Basin

尽管通过频谱分析法能从替代指标的时间(或深度)域数据中很好地计算出其包含的主要频率(周期)成分，但其分析得到的结果仅为一段时间(或深度)内的平均谱结构，不能反映出频率域随时间(或深度)的变化信息，也不能对地层的沉积速率在各个地质历史时期的变化情况有良好反映，而经验模态分解(Empirical Mode Decomposition，简称EMD)法则能较好的解决这一问题[27]。由于EMD方法相较于小波变换法更适用于测井数据这一类非线性与非平稳态序列，运用EMD法对测井数据提取局部均值曲线，其将复杂信号分解得到一系列固有模态函数(Instrinsic Mode Functions，简称IMF)。每一个函数分量中都包含了信号的完成信息，选择一组合适且最符合地质研究目标的IMF则更能直观反映序列的频谱分析结果[24]，特别在对高频沉积旋回准确客观识别过程中更能充分凸显其“数学显微镜”的作用，克服了小波变换中小波基选取的约束。

首先，根据顺托果勒地区志留系柯坪塔格组频谱分析识别出的斜率旋回周期(38.1 ka)，可以计算出地层沉积时限：(435 m÷1.59 m)×38.1 ka=10.4 Ma。其次，根据得出的柯坪塔格组的沉积时限计算结果，我们可得到对应125 ka偏心率周期的五级层序发育个数，即：

10.4 Ma÷125 ka≈83个

(1)

另外，对顺9井自然伽马测井曲线进行EMD分解得到IMF1—IMF9 共计9个固有模态和一个残余项R(图4)，结果表明：顺9井柯坪塔格组中可能存在作为五级层序划分标尺的短偏心率周期125 ka，在参照岩性变化特征及测井曲线变化特征下，以柯坪塔格组底部为开始对与之相对应的高频旋回地层进行划分。采用计数法得到顺9井柯坪塔格组对应于125 ka周期保存了约83个短偏心率周期旋回，对应于固有模态函数IMF3。因此，再结合先前计算出的柯坪塔格组平均沉积速率，以旋回信号清晰、相对稳定的短偏心率旋回125 ka为标准，建立了柯坪塔格组高分辨率“浮动”天文年代标尺(图5)，使得顺9井柯坪塔格组中每一深度位置的地质年龄都能做出较为精确的估计。同时，我们可合理的认为，若对有地层剥蚀现象的井如顺3、顺4井等进行上述频谱分析和计算，能够近似的得出该井的地层剥蚀量，本文不在赘述，特列出计算公式如下：地层剥蚀量=10.4 Ma÷斜率周期×斜率,对应平均旋回厚度-现今地层厚度。

5 可容空间变化

可容纳空间变化是形成沉积层序的本质因素。从理论上来说，随着可容纳空间的周期性变化，沉积物的叠加样式和沉积体系的发育也呈周期性变化[28]。在绘制Fischer图解时，横坐标表示地层厚度，纵坐标表示高频旋回的累计厚度偏移，对测井曲线数据处理遵循：①消除测井曲线长趋势化偏移；②运用钟形函数5点加权滑动平均法去除曲线无关的毛刺干扰，突出沉积旋回的周期波动变化；③采用一阶差分法和极值判别法计算沉积旋回厚度[29]。

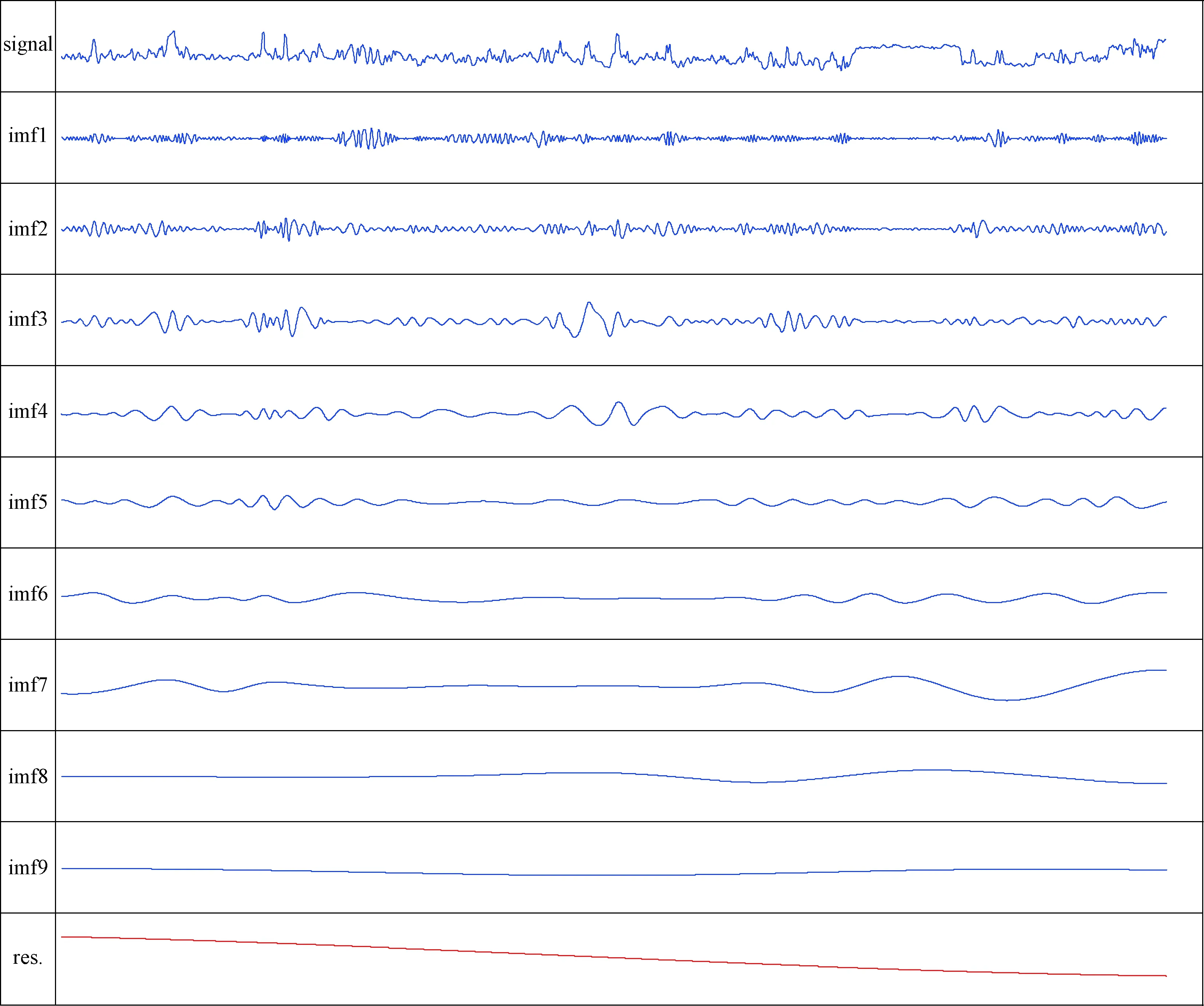
图4 塔里木盆地顺9井GR曲线EMD分解图Fig.4 EMD diagram of GR logs from Well Shun-9,Tarim Basin

通过对柯坪塔格组GR曲线进行Fischer图解(图6)，并结合前文建立的“浮动”天文年代标尺可知：柯坪塔格组可划分为1个二级层序、4个三级层序、26个四级层序及83个五级层序，观察可知各级高频旋回具有明显的不对称性，并且各级旋回之间叠加比均体现出变化。其中，三级层序界面分别对应井深约5 561.4,5 450和5 336 m的位置，界面相应岩性为灰色细砂岩、灰色中砂岩和灰色细砂岩。第一个三级旋回层序由5个四级旋回层序和20个五级旋回层序叠加组成，对应厚度约为87.9 m；第二个三级旋回层序由7个四级旋回层序和24个五级旋回叠加组成，对应厚度约为111.4 m；第三个三级旋回层序由5个四级旋回层序和17个五级旋回叠加组成，对应厚度约为114 m；第四个三级旋回层序由9个四级旋回层序和22个五级旋回叠加组成，对应厚度约为130 m。究其原因，我们推测主要为在潮坪沉积环境中旋回形成时的地层堆积作用所导致，由于波浪和潮汐的改造作用，使前期未固结成岩的旋回地层出现沉积缺失，并且改造作用越大，这种缺失越明显，随之产生各级旋回叠加比的变化;同时，潮坪沉积物主要依靠潮汐回流从陆源区带入，当海平面快速上升时，由于个别区域沉积物供应不足而导致形成比较单一的潮下非补偿性小旋回，而后续旋回便直接发育其上，造成前后或更多的旋回叠加；当海平面快速下降时，原有沉积的旋回上部会遭受侵蚀，从而形成两个旋回的兼并。正是由于这些情况造成的旋回叠加和兼并，各级旋回的不对称性和组成各级旋回的比率变化在所难免。

从旋回变化趋势曲线可以看出，受125 ka短偏心率控制的沉积旋回经历了83次高频海平面升降变化，且每个沉积旋回都经历了一次可容纳空间由小变大再减小的过程，其他更低频次的旋回也有同样的增加—减小的过程。以三级层序可容纳空间演化为例，柯坪塔格组第一次可容纳空间持续约为2 Ma，可容纳空间呈现由快速增加变为快速减少的趋势;第二次可容纳空间持续时间约为2.8 Ma，呈现由较快速增加变为缓慢减少的趋势;第三次可容纳空间持续时间约为2 Ma，呈现由缓慢增加变为快速减少的趋势;第四次可容纳空间持续时间约为3.6 Ma，呈现由快速增加变为快速减少的趋势。

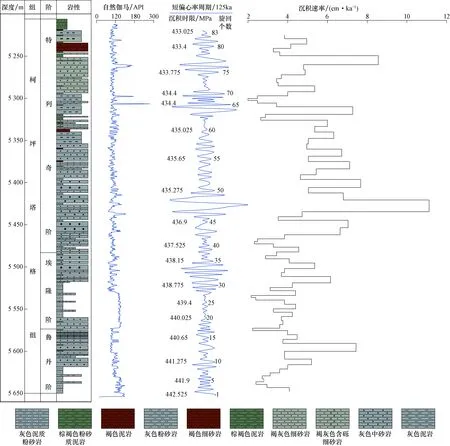
图5 塔里木盆地顺9井岩性剖面、“浮动”天文年代标尺及沉积速率综合图Fig.5 Composite chart showing lithology,“floating” astronomical time scale and sedimentary rate of Well Shun-9,Tarim Basin

同时在三级层序可容纳空间上升过程中，发育多套潮下带中-细砂岩、泥质粉砂岩和薄层泥岩组成的退积型旋回地层，而在可容纳空间下降过程中，发育潮间带薄砂泥岩互层、细砂岩的加积-进积旋回地层。

6 结论

1) 通过自然伽马测井曲线频谱分析法发现，柯坪塔格组沉积地层中保存完好的米兰科维奇旋回，天文轨道参数参数比与识别出的地层旋回厚度比率一致，受控于405 ka的长偏心率周期影响的旋回厚度为16.73 m，125 ka和95 ka短偏心率周期影响的旋回厚度为5.24和3.92 m，受控于38.1 ka和31.1 ka的斜率周期影响的旋回厚度为1.59和1.26 m，揭示出天文轨道旋回在塔里木盆地柯坪塔格组沉积过程中具有明显影响，其中偏心率对该区域地层影响最大。

2) 柯坪塔格组的沉积时限约为10.4 Ma，其中共记录了83个125 ka周期短偏心率旋回和334个31.1 ka周期斜率旋回，分别对应于层序地层学中的五级和六级层序，证明米兰科维奇旋回对高频层序发育具有稳定的控制作用，可为高频层序的划分方案建立时间标尺，显著提高了高频层序划分的统一性，客观性。

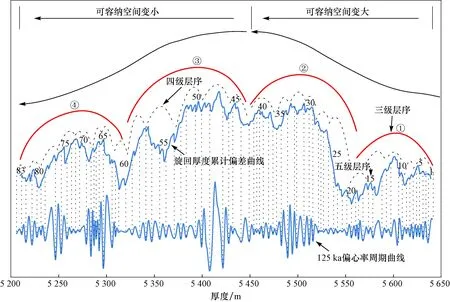
图6 塔里木盆地柯坪塔格组Fischer图解与可容纳空间变化趋势Fig.6 Fischer interpretation and trend of accommodation variation of the Kepingtage Formation,Tarim basin

3) 基于米兰科维奇计算得到塔里木盆地柯坪塔格组沉积速率为4.15 cm/ka，结合EMD分解法以125 ka短偏心率旋回周期为标准，建立了柯坪塔格组具有相对时间概念的“浮动”天文年代标尺，大大提高了小规模旋回的识别，该天文标尺可对顺9井柯坪塔格组地层中每一深度位置的地质年龄和任一层段的沉积时限都能做出较为精确的估计，进而可估算出任一层段的沉积速率，总结出了一种有助于计算和对比沉积速率变化的新方法。

4) 依托天文年代标尺和Fischer图解的结合，对可容纳空间变化及高频旋回叠置关系进行分析，对三级层序划分、对比及层序沉积模型建立具有指导意义。结果显示柯坪塔格组各级沉积旋回均经历了可容纳空间上升—下降的过程，可划分出1个二级层序，4个三级层序，26个四级层序，83个五级层序及334个六级层序，各级旋回之间的叠置比均存在变化，大多数六级旋回按4 ∶1的比率向上叠加为五级旋回，少数为5 ∶1的比率向上叠加，而五级旋回主要按3 ∶1的比率向上叠加为四级旋回，只有顶部的按照4 ∶1比率叠加。为此，本文提供了一个对不同级别高频旋回叠置关系分析的新手段。