基于地脉动谱比法的场地特征参数快速测定

刘宇实， 师黎静

(1.中国地震局 工程力学研究所 地震工程与工程振动重点实验室，哈尔滨 150080；2.国家知识产权局专利局专利审查协作四川中心，成都 610213)

对于工程地震和岩土工程领域而言，简便性、高效性、易用性始终是决定方法是否被广泛使用的关键因素。正因为如此，世界各国的抗震设计规范、经验性的地震动预测模型、新一代衰减关系研究和相关的地震区划工作中，都不约而同地采用了等效剪切波速、覆盖层厚度(或称基岩埋深)和特征周期等简化指标来考虑场地条件影响[1-3]。

传统波速测试方法，如钻孔法、地震勘探法等昂贵、耗时、耗力，不利于大规模地开展应用，很多情况下都缺少相关的特征参数。在美国NGA-west2中50%的台站有场地等效剪切波速Vs30，而NGA-east中仅6%的台站有Vs30[4]。与美国相比，我国的强震台站的场地信息更不完善，严重影响了宝贵强震数据的利用。另外，在历次大地震后的震害调查和科考中，也因缺少快速的测定手段，对场地条件只能靠经验定性地进行判定，影响了对地震动和震害分布特征的分析。急需发展这些参数的快速测定技术，才能使新的研究成果迅速推广应用。而地脉动方法，尤其是单点H/V谱比法而恰恰在简便、快速方面有独特的优势。

自地脉动H/V谱比法提出以来，一直受到广大工程地震研究人员的关注，进行了大量理论和应用研究。目前研究者已得到共识，地脉动H/V谱比卓越频率与地震动的卓越频率一致。国际上，研究者进一步将地脉动H/V谱比的峰值幅值与场地效应建立联系，建立了峰值频率与场地的覆盖层厚度拟合关系[5-8]，并在地震区划和小区划中进行了应用。但是整体上看，对单点谱比与场地各特征参数之间的相关性，区域间的差异等认识还比较模糊，与场地等效剪切波速和等效周期之间关系的研究还很少。

本文搜集了37个场地钻孔和波速测试资料，并在这些场地进行地脉动单点观测，研究地脉动H/V谱比，主要是卓越频率与场地覆盖层厚度、等效剪切波速和特征周期等特征参数之间的相关性，对比分析不同研究者给出的不同地区各相关关系，讨论利用地脉动单点观测快速测定场地各特征参数的精度。

1 场地钻孔波速数据和地脉动单点观测

本文共搜集到37个场地钻孔和波速测试资料[12]，分布如图1(a)。场地土层以杂填土、粉质黏土、细砂、中砂、粗砂和泥岩为主，所有钻孔都钻到了泥岩层。覆盖土层最深达90 m，最浅21 m。所有钻孔均进行了波速测试，剪切波速结构如图1(b)。从图可见，剪切波速整体上是随深度递增的，终孔地层的剪切波速Vs均大于500 m/s，各个场地钻孔资料统计结果参见表2。各类土层的剪切波速，杂填土层一般在120 m/s左右；粉质黏土土层变化较大，从124 m/s到454 m/s；砂层在280 m/s到450 m/s之间；泥岩达到500 m/s以上。37个场地的等效剪切波速Vs20最小158 m/s，最大221 m/s，等效剪切波速Vs30最小181 m/s，最大246 m/s，Vs30比Vs20平均略高26 m/s左右。

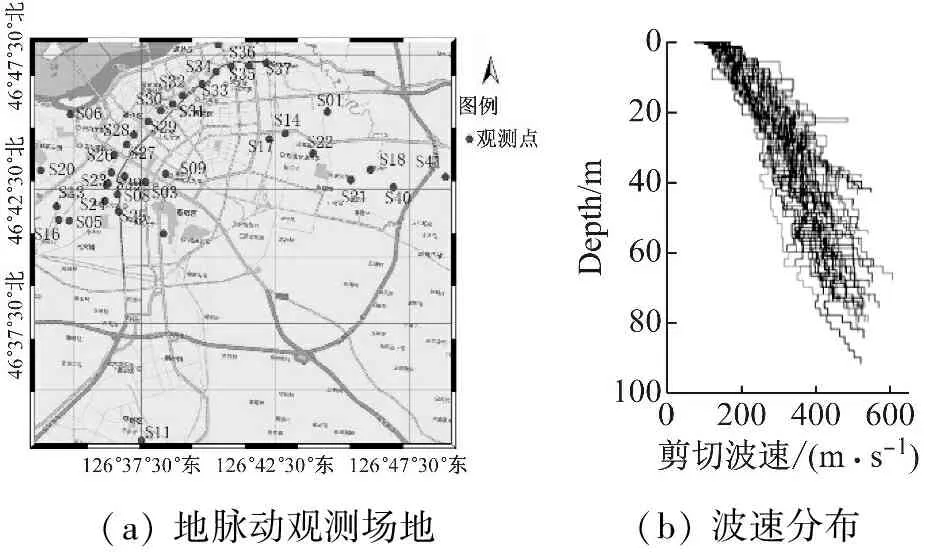
(a) 地脉动观测场地(b) 波速分布

图1 地脉动观测场地和波速分布

Fig.1 Microtremors observation sites and velocity structures

在37个场地钻孔附近进行了地脉动单点三分量观测。观测采样频率100 Hz，观测时间长度10～60 min不等，随覆盖层厚度增大，观测时间相应增加。现场观测采用的仪器为TAG-33M三分量力平衡加速度仪。

2 地脉动H/V谱比分析

2.1 地脉动H/V谱比计算

地脉动时域信号并不能显示场地的动力特性，需要对地脉动时域信号经傅里叶变换转换为频域信号，进行了东西和南北两个水平分量的合成，国内外不同研究中的处理方式不尽相同。本文首先，对比考察了根据不同公式合成水平分量、傅里叶变换窗函数选择及光滑函数对H/V谱比的影响，最终选择合理的方法进行地脉动H/V谱比计算。

两个水平分量的合成方式有平方根法(RS)、乘积开方法(RM)、均方根(RMS)法和平均值法(Mean)四种，分别见式(1)～(4)。

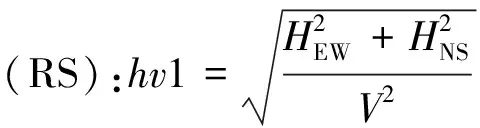
(1)

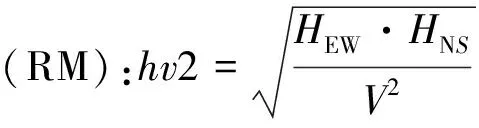
(2)

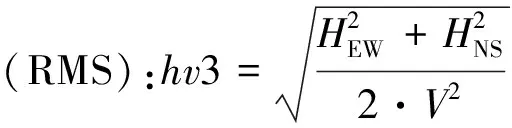
(3)

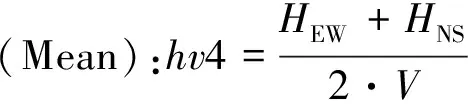
(4)

首先，采用相同的长20.48 s矩形窗和10点光滑函数，计算NS方向、EW方向和UD方向的傅里叶谱，分别采用4种平均方式计算场地S23的H/V谱比，结果如图2(a)所示。从图2(a)中可以看出，4种平均方式得到的卓越频率完全一致，乘积平方根法和均方根法的结果幅值基本相同，平方根结果幅值偏大，平均值法结果幅值偏小。

其次，同样采用均方根法合成水平分量和10点光滑函数，考察施加矩形窗、海明窗、汉宁窗和布莱克曼窗等不同窗函数进行快速傅里叶变换时，对H/V谱比计算结果的影响。分别对场地S23的地脉动记录施加长度为20.48 s的这四种窗函数，不同窗函数下的计算结果如图2(b)所示。由图可见，加海明窗、汉宁窗和布莱克曼窗的H/V谱比结果基本一致，而加矩形窗的H/V谱比曲线峰值幅值较小，峰值频率较大。

最后，考察光滑点数分为2点、3点、5点、10点和20点对H/V谱比计算结果的影响。同样以场地S23为例，计算窗口长度为20.48 s，分别计算NS方向、EW方向和UD方向的傅里叶谱，用均方根(RMS)方法合成水平分量，并求多次计算结果的平均值，其计算结果见图2(c)，当光滑点数逐渐增加时，场地的卓越频率也随之变换，但是没有明显的变化；H/V幅值逐渐变小，10点光滑函数结果，卓越频率较清晰，利于识别，对幅值的影响也相对较小。

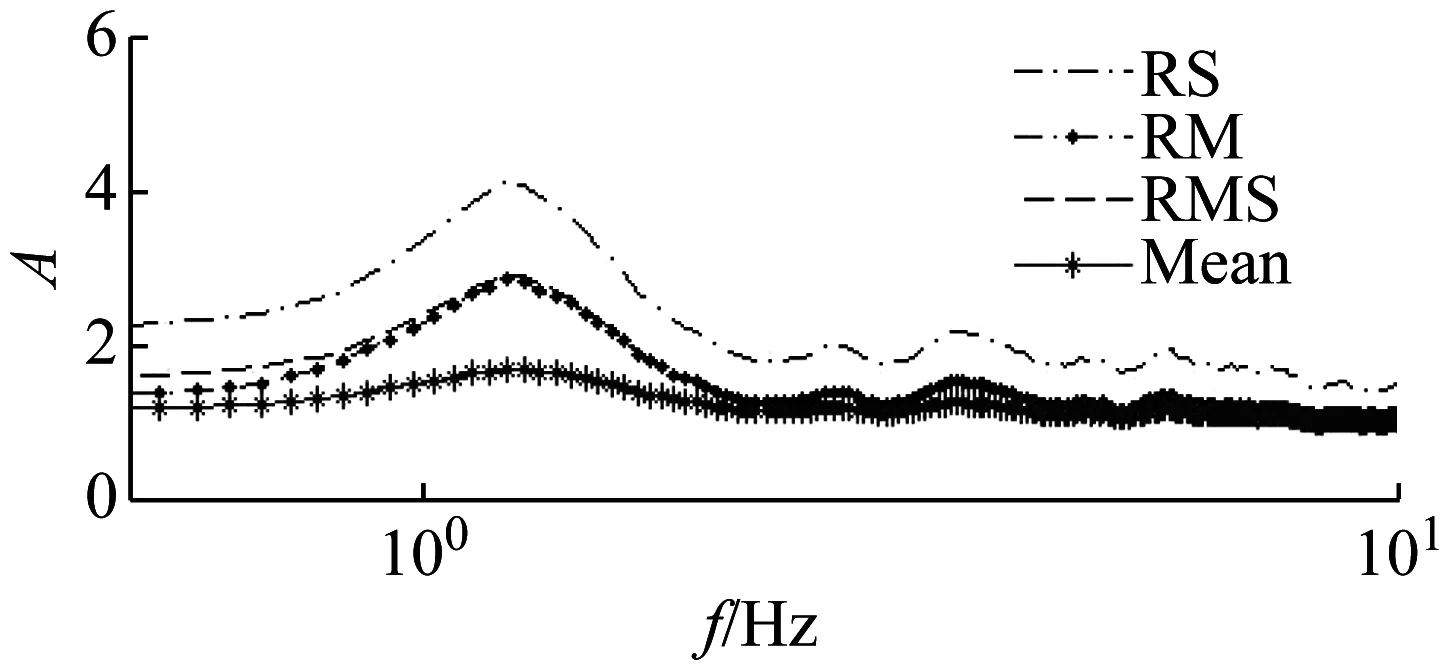
(a)不同水平分量合成方式

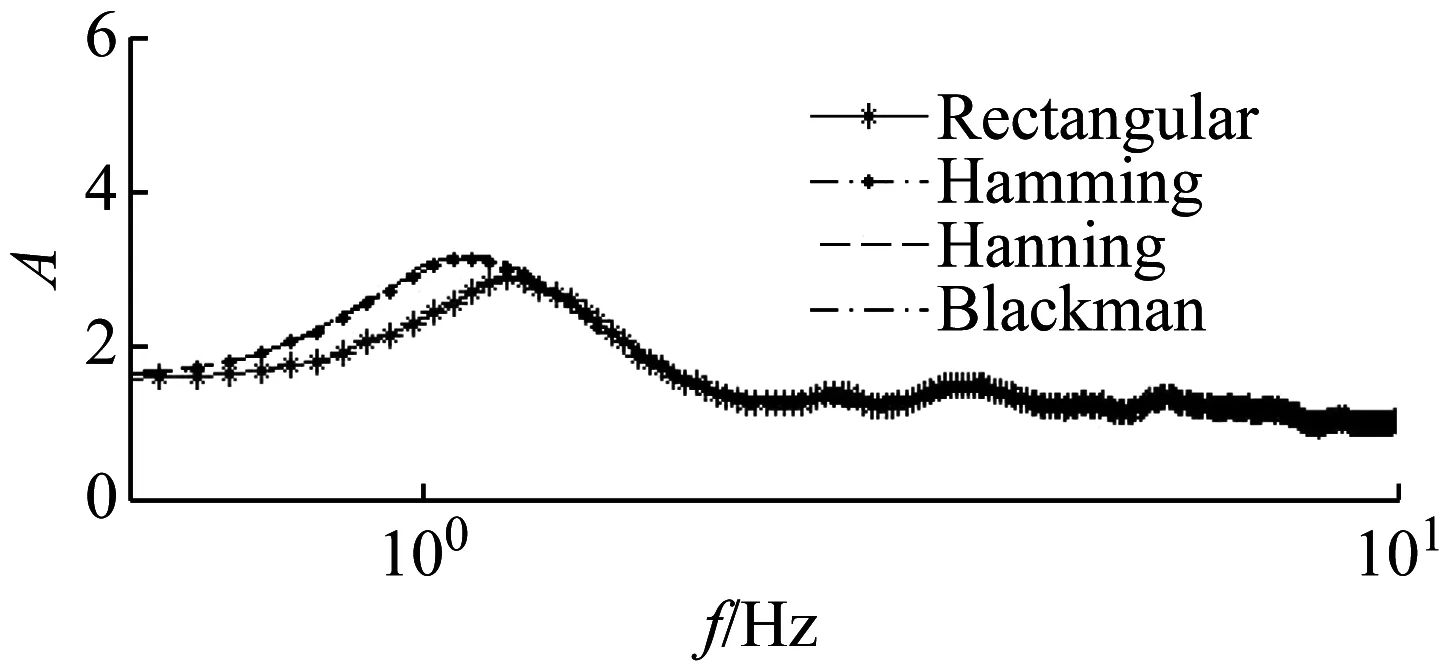
(b)不同窗函数

(c)不同光滑函数点数

Fig.2 Comparison of H/V spectra computed with different horizontal component combinations, spectra windows and smooth points number

在上述比较考察基础上，本文采用加窗长为20.48 s的汉宁窗，10点平均光滑，计算水平分量和竖向分量的傅里叶谱，通过均方根法合成两个水平分量，计算分析了37个场地的地脉动H/V谱比。作为一例，图3给出了场地S23的地脉动记录、傅里叶谱及H/V谱比曲线。

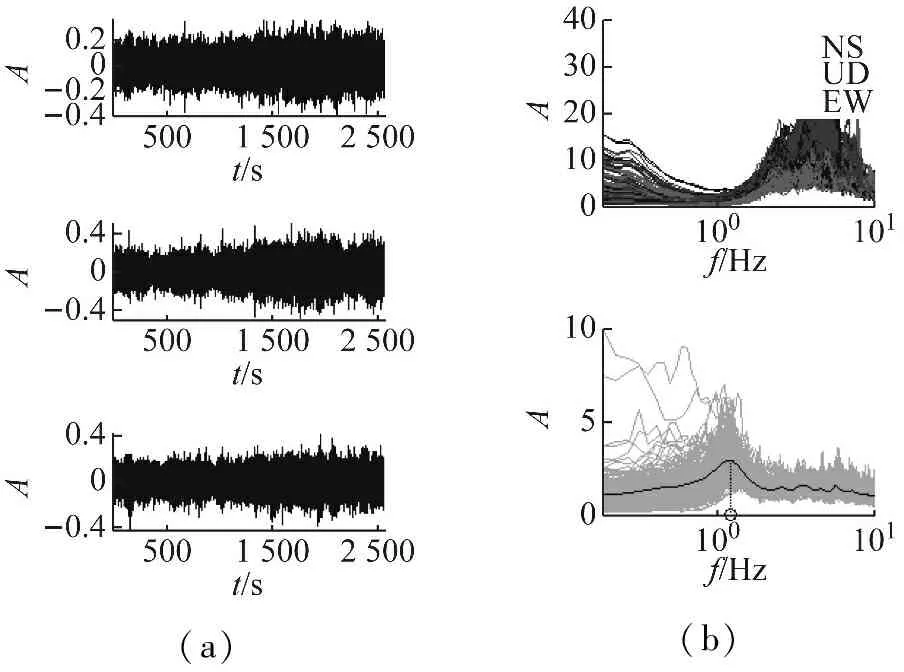
(a)(b)

图3 场地S23地脉动三分向记录、傅里叶谱及H/V谱比曲线

Fig.3 Microtremors 3-components timehistories and Fourier spectra and H/V spectra at site S23

2.2 谱比可靠性检验与卓越频率确定

地脉动观测受现场观测场地条件、环境干扰和仪器设备稳定性和布设等因素影响，需对场地地脉动H/V谱比计算结果可靠性进行检验。欧盟SESAME研究给出的地脉动H/V谱比可靠性准则和峰值清晰准则[14]，认为，同时满足以下三条准则，场地地脉动H/V谱比才是可靠的：

(1)场地卓越频率应大于计算傅里叶谱窗口长度倒数的10倍；

(2)显著周期数应大于200个；

(3)如果场地卓越频率大于0.5 Hz，在区间[0.5f0,2f0]之间的卓越频率幅值的标准差应小于2；如果场地卓越频率小于0.5 Hz，在区间[0.5f0,2f0]之间，卓越频率幅值的标准差应小于3。

同时，地脉动H/V谱比曲线应满足以下六条准则中的五条，才认为其峰值清晰卓越。

(1)在[f0/4,f0]之间，存在f-使得H/V谱比曲线幅值小于卓越频率处峰值的二分之一；

(2)在[f0,4f0]之间，存在f+使得H/V谱比曲线幅值小于卓越频率处峰值的二分之一；

(3)卓越频率峰值幅值应大于2；

(4)H/V谱比曲线加减H/V谱比曲线幅值标准差后的峰值位置应落在卓越频率±5%以内；

(5)卓越频率标准差应小于阈值ε(f0)；

(6)卓越频率峰值标准差应小于阈值θ(f0)；阈值ε(f0)和θ(f0)的值见表1。

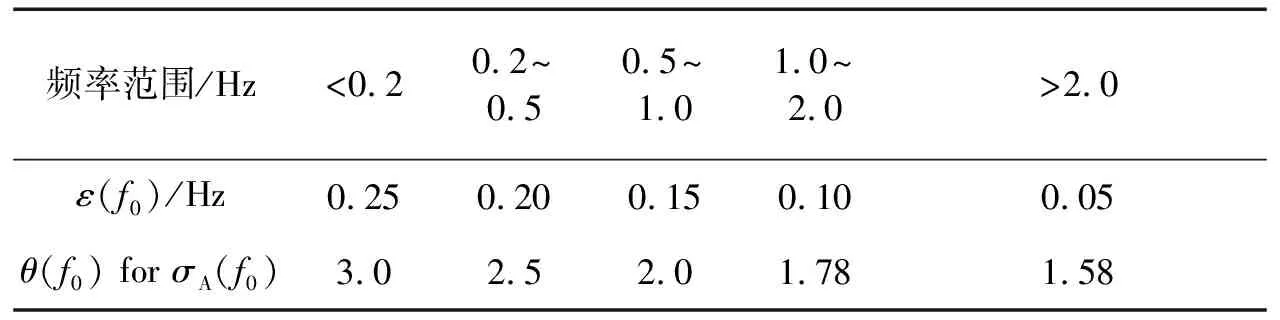
表1 σf和σA(f0)的阈值

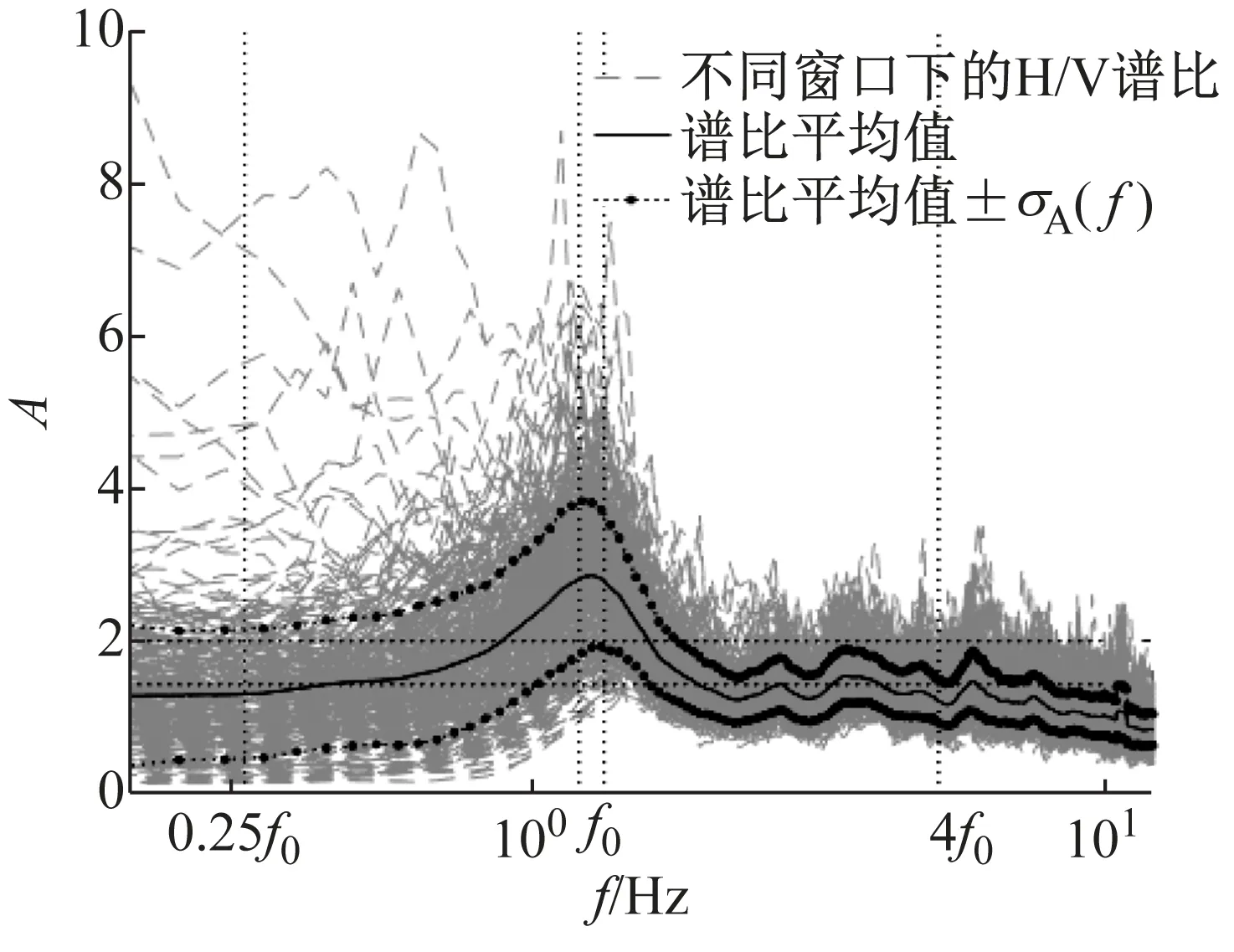
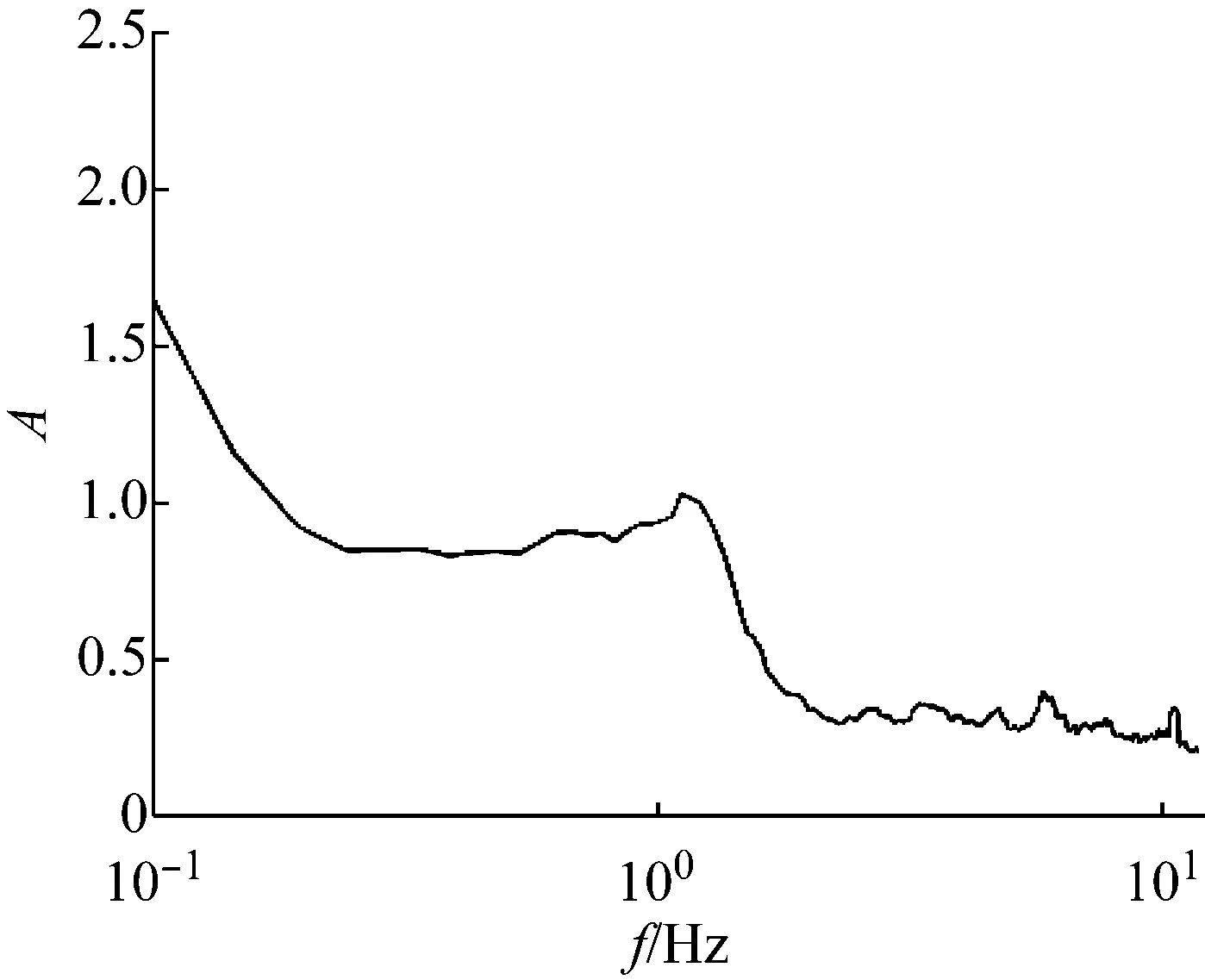
本文采用上述准则，检验37个场地地脉动H/V谱比的可靠性，进而确定卓越频率。以场地S23为例(如图4)，其H/V谱比曲线满足3条可靠性准则和5条峰值清晰准则，因此认为，观测分析的场地S23地脉动H/V谱比可靠且峰值清晰。其他场地的地脉动H/V谱比均采用该准则进行了检验，对不满足准则的场地进行了重新观测，最终37个场地地脉动H/V谱比曲线全部满足了可靠性准则。其中，有20个场地谱比曲线(图5)满足峰值清晰准则，还有14个场地的结果(图6)虽然不完全满足峰值清晰准则，但是根据哈尔滨场地条件特征和参考其它场地观测结果，可以确定与场地条件相关的地脉动H/V卓越频率。另外三个场地(图7)的结果不能确定卓越频率位置，予以剔除。

(a)

(b)

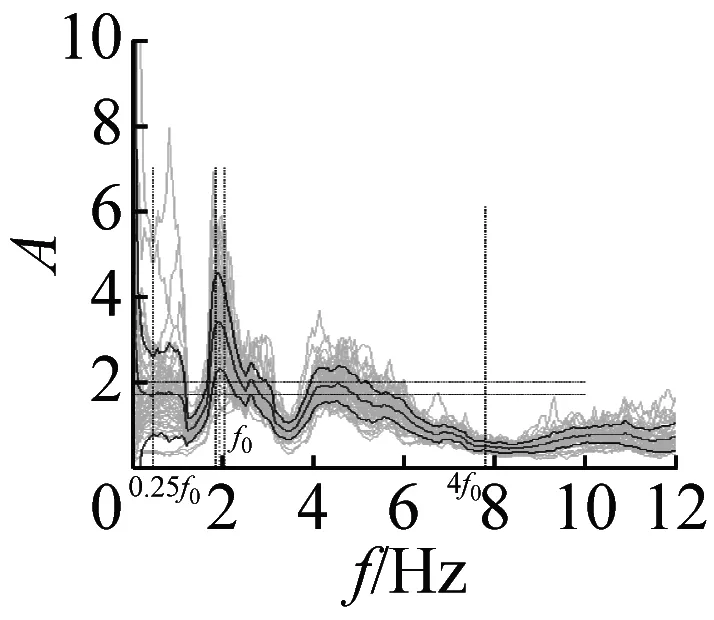
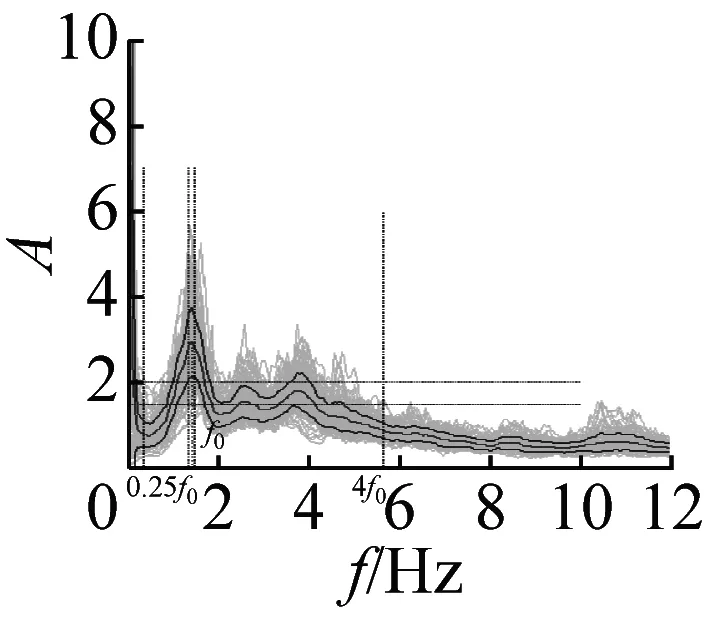
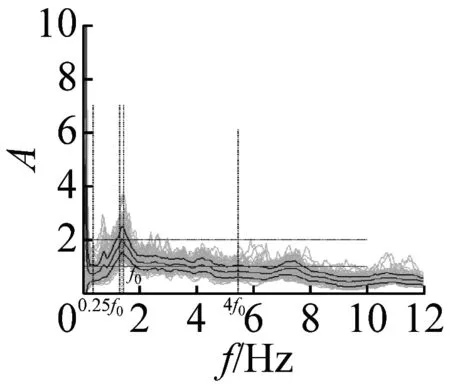
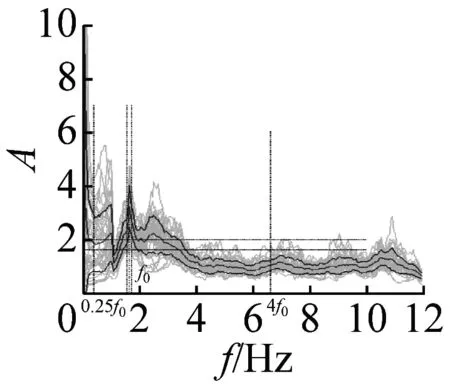
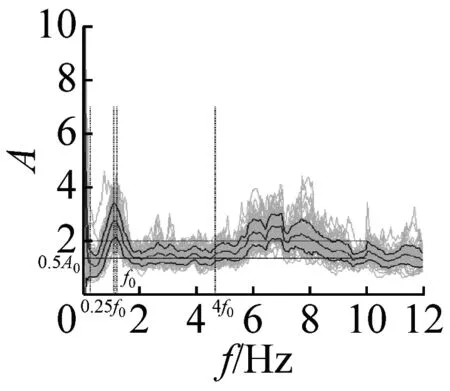
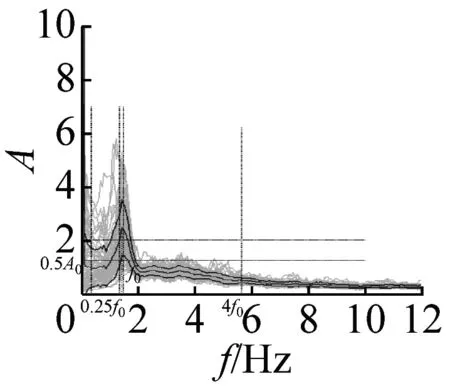
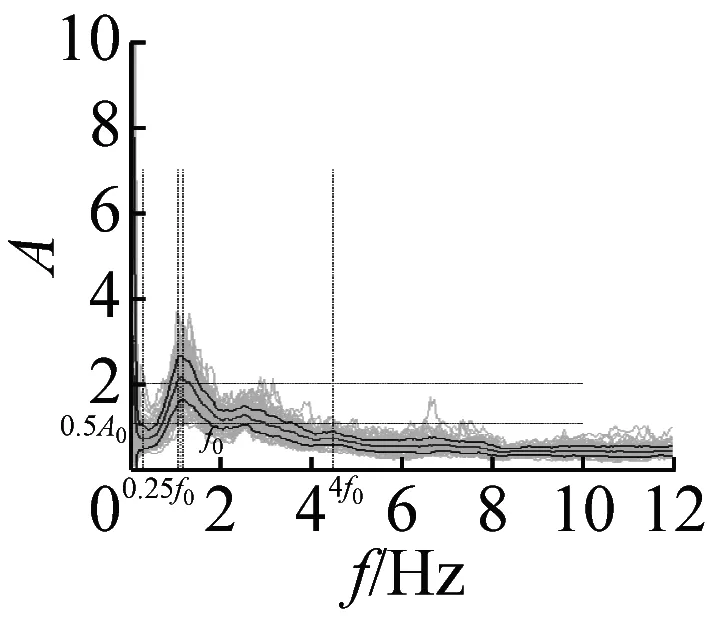
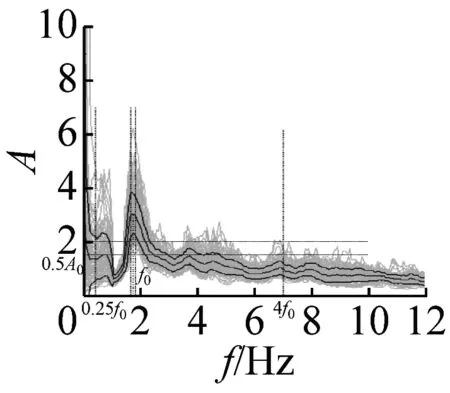
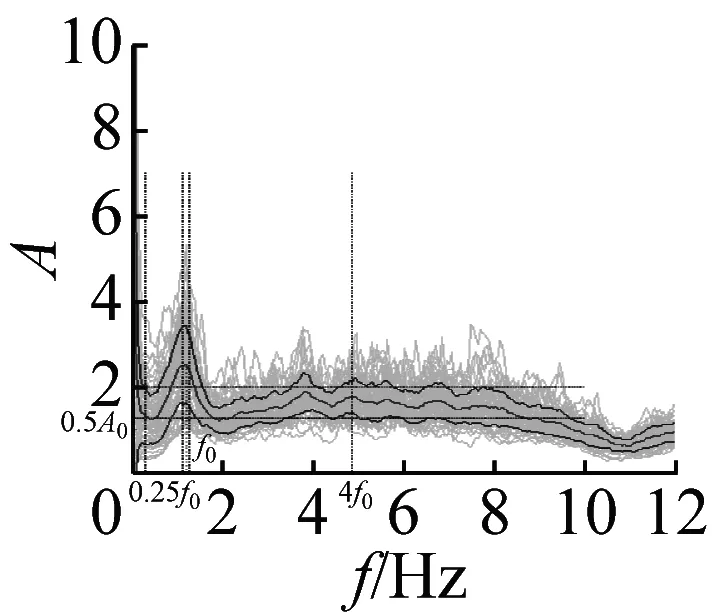
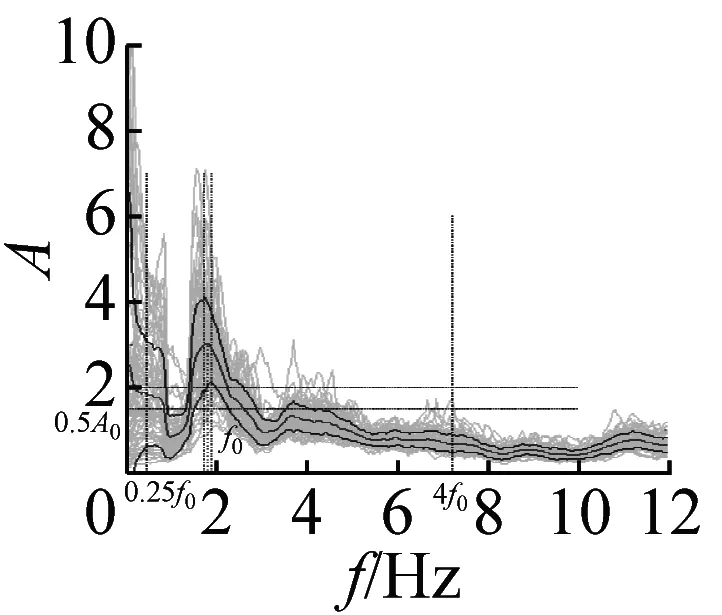
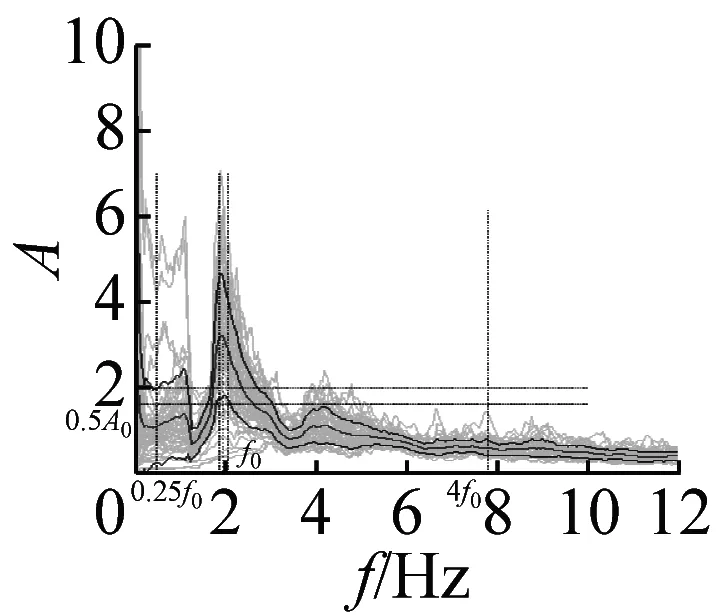
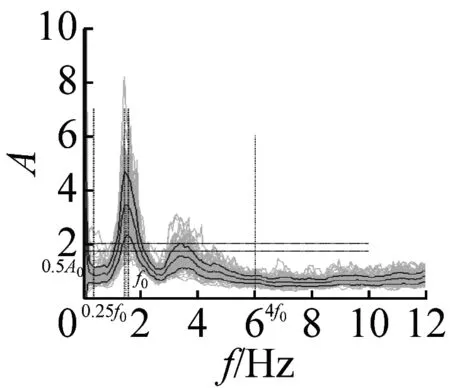
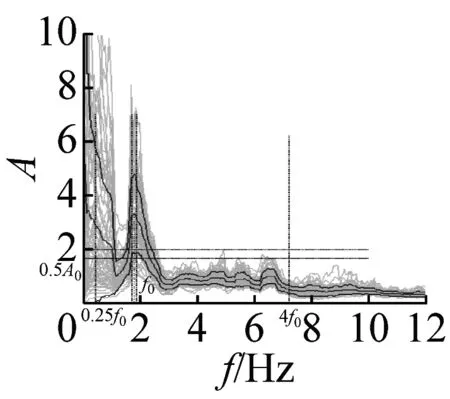
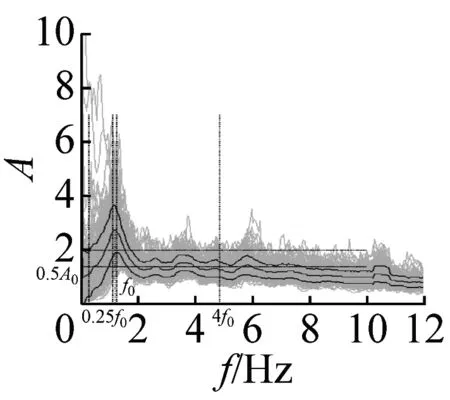
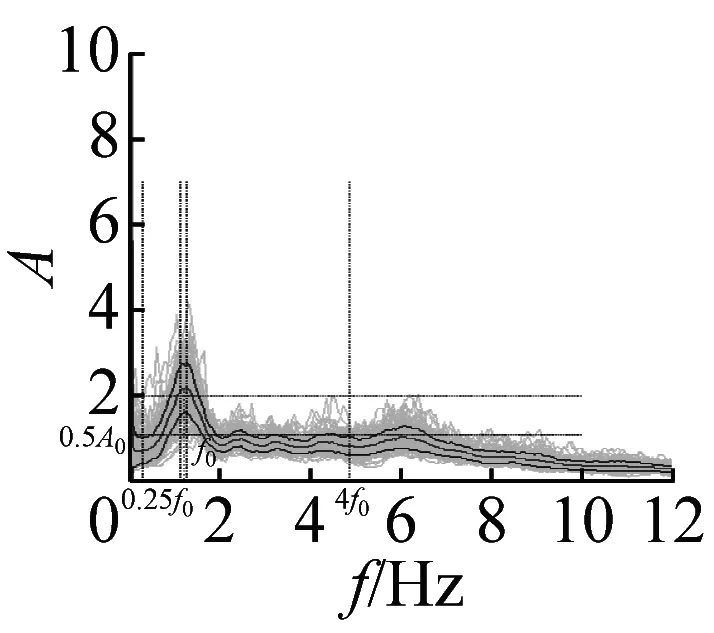
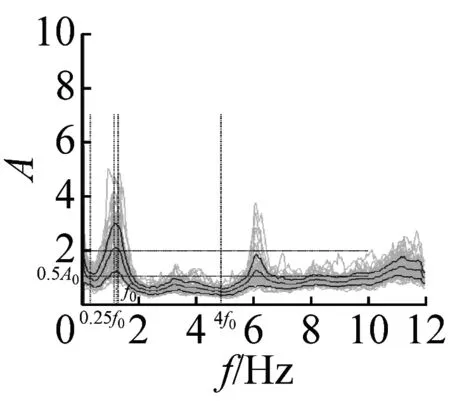
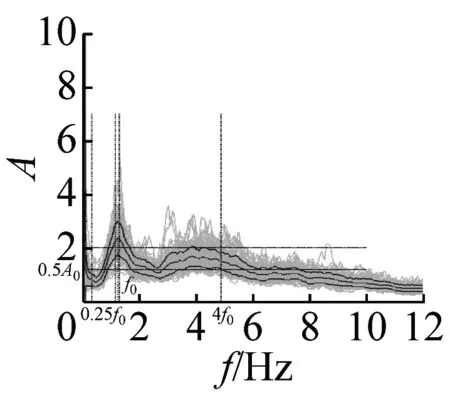
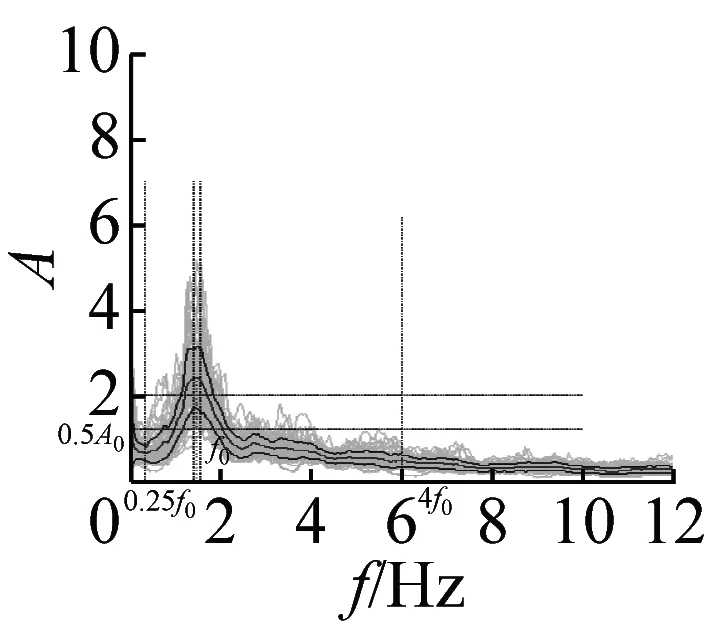
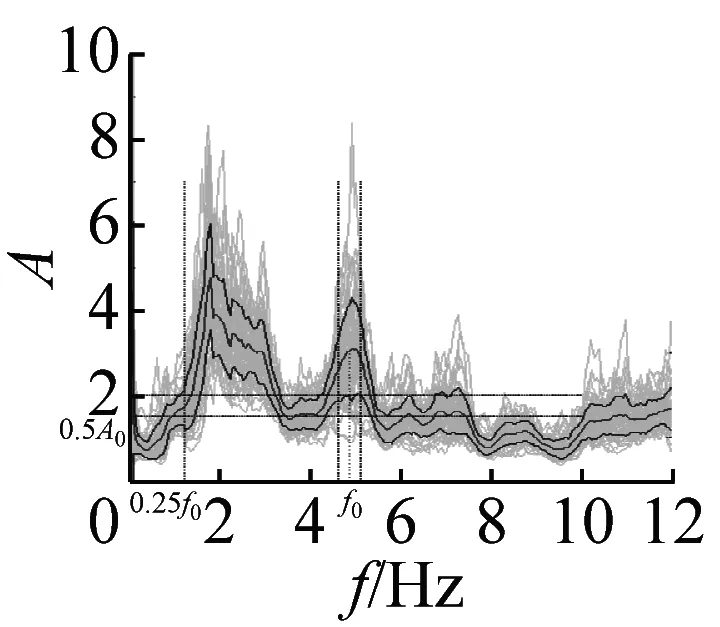
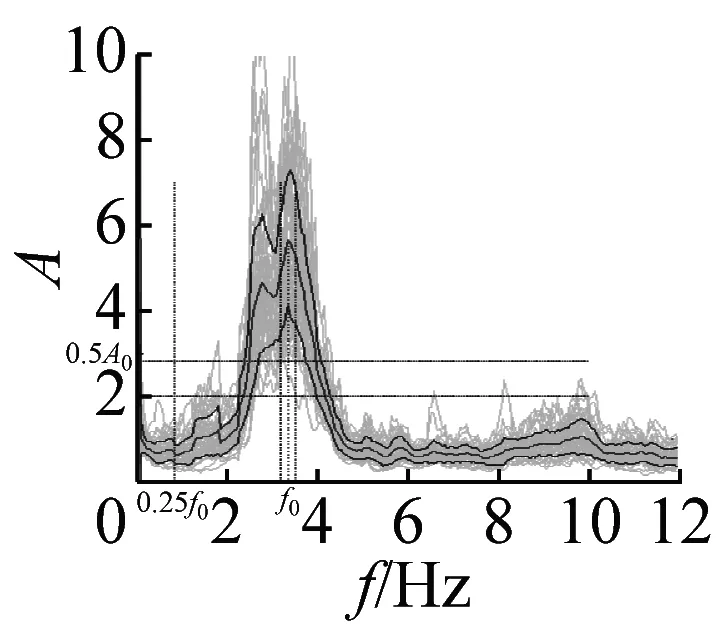
图5 峰值清晰的20个地脉动H/V谱比

本文37个场地观测的地脉动，参见表2，从卓越频率分布范围来看，H/V卓越频率主要分布在1～2 Hz以内；从幅值比来看，最大H/V峰值频率幅值比为5.66，最小幅值比为1.32，其中幅值比大于2的场地有27个，没有小于1的情况；从谱比波形来看，大部分H/V谱呈现单一波峰波形，共有28个场地，另外有8个场地出现两个波峰，1个场地波峰不明显，没有场地出现3个及以上波峰情况。

3 地脉动H/V谱比卓越频率与场地特征参数相关性分析

3.1 地脉动卓越频率与覆盖层厚度

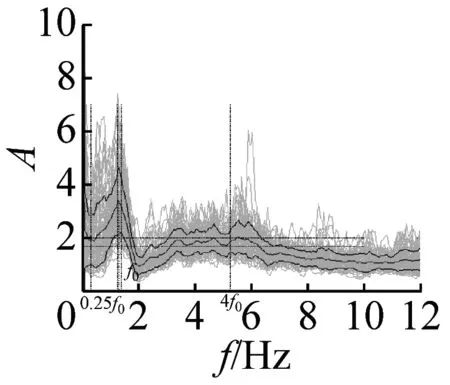
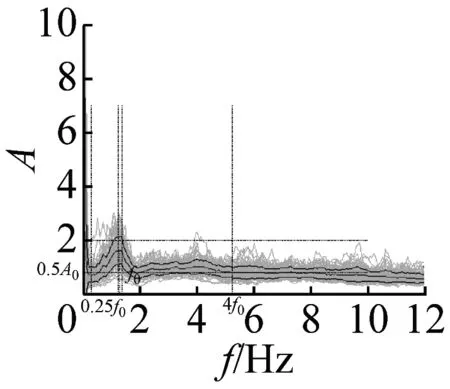
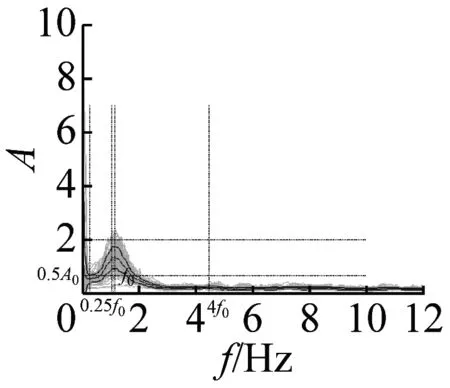
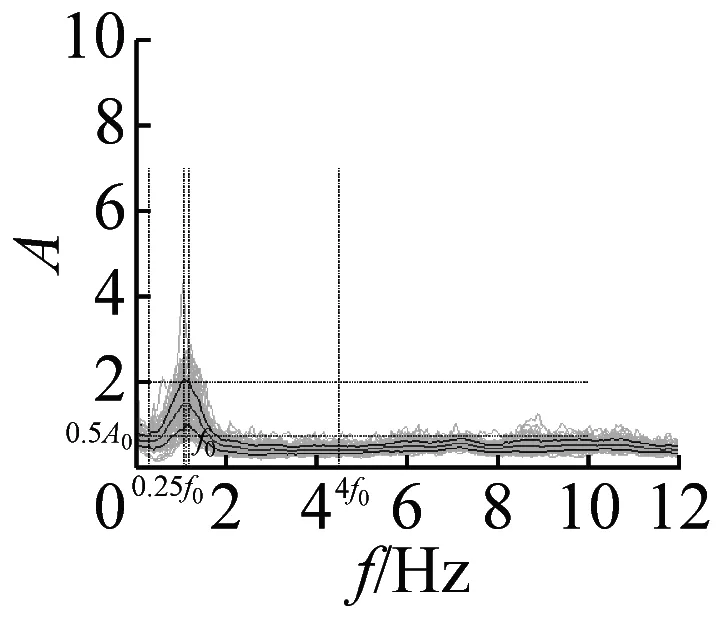
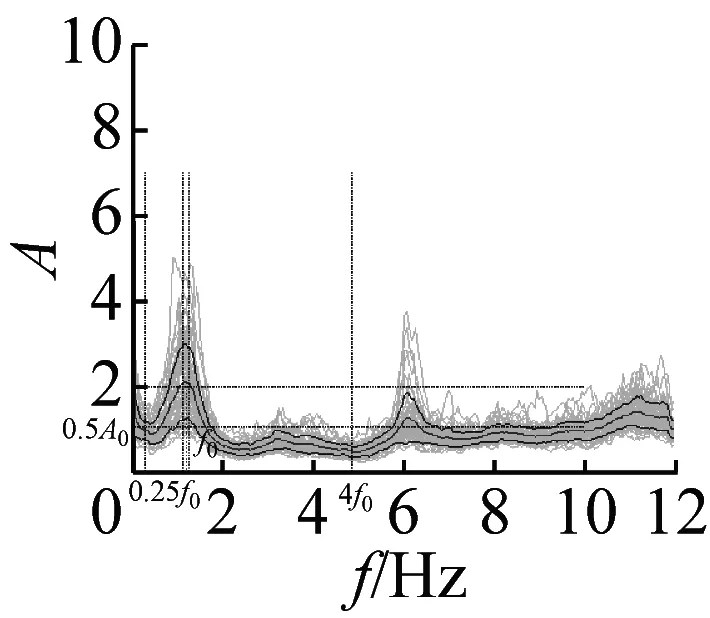
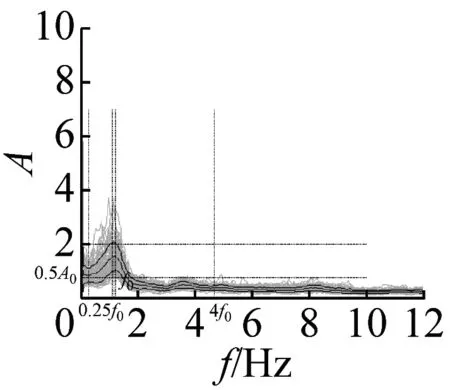
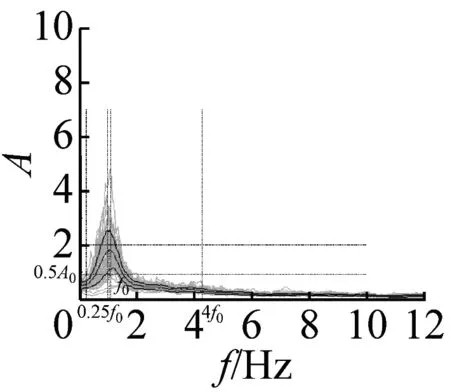
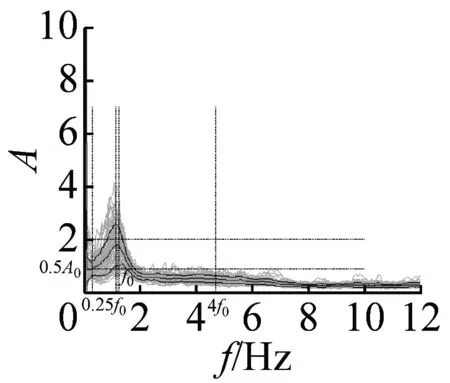
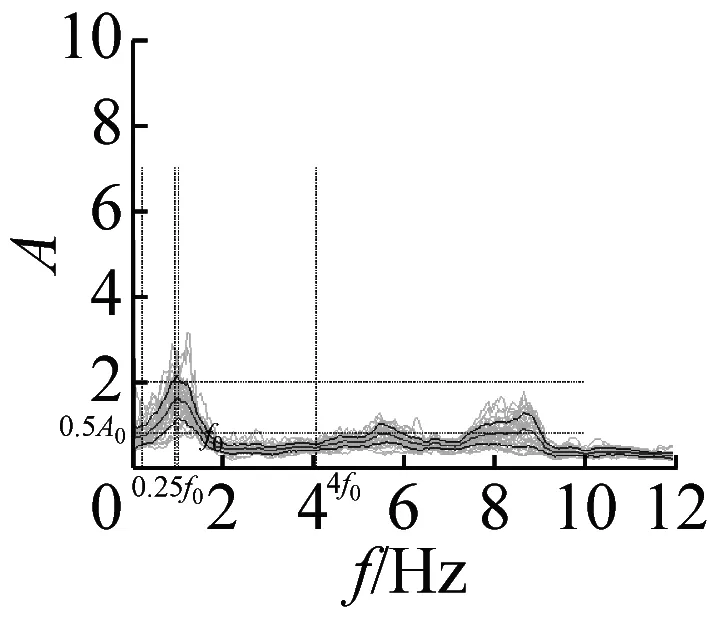
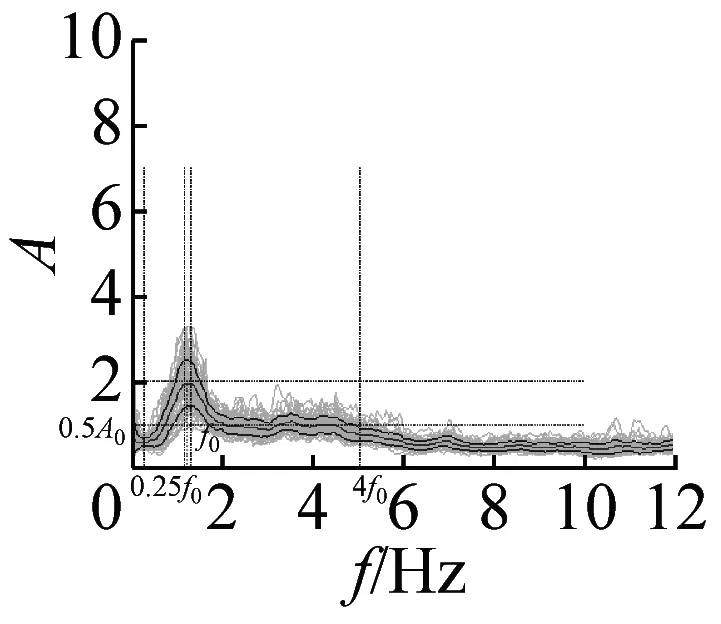
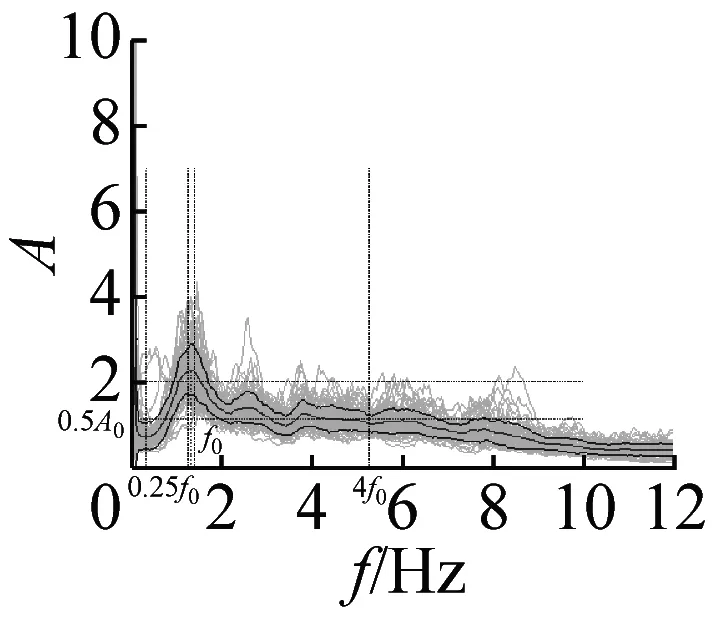
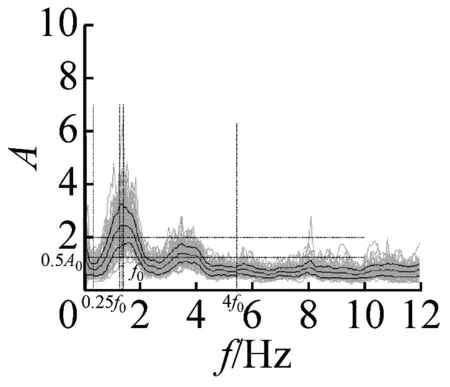
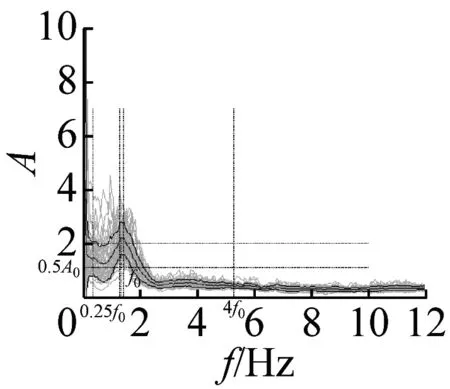
图6 不完全满足峰值清晰准则14个地脉动H/V谱比

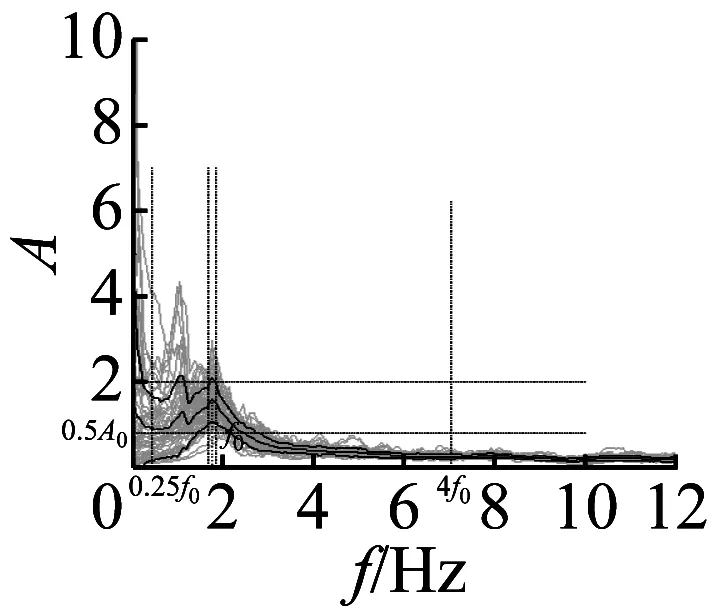
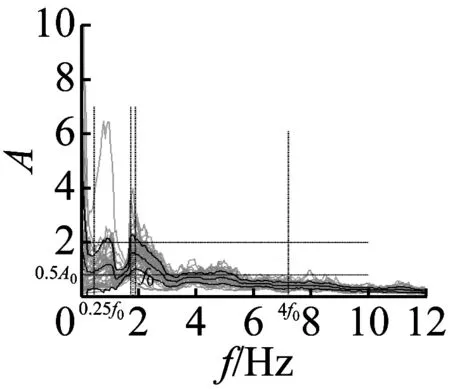
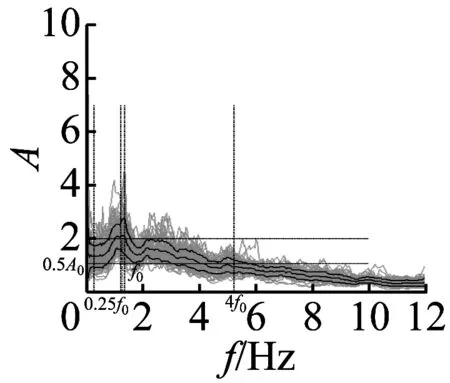
图7 峰值频率不清晰的3个地脉动H/V谱比

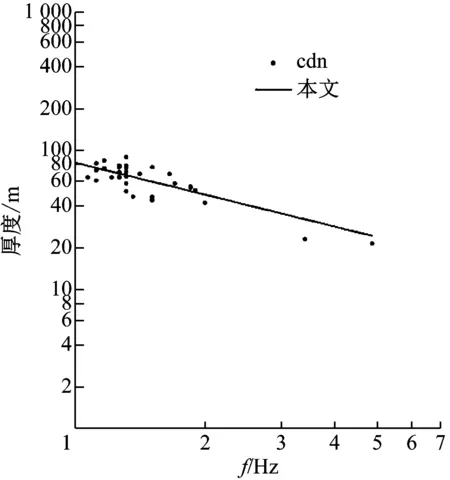
各场地地脉动H/V谱比结果显示，场地S40的卓越频率最大，为4.88 Hz，该场地的覆盖层厚度为22 m；场地S31的卓越频率最小，为1.07 Hz，该场地的覆盖层厚度为75 m。图8给出了场地的覆盖层厚度与H/V谱卓越频率。由图可见，地脉动谱比卓越频率随着场地覆盖层厚度的增加而呈现减小的趋势，二者有很强的相关性。单点H/V谱比法得到的场地卓越频率与场地的覆盖层厚度相关性研究中，大多采用幂指数关系(5)。从图8结果来看，本文场地地脉动也符合这一关系。采用式(5)的形式，对测得的地脉动卓越频率和有钻孔资料得到的覆盖层厚度进行了拟合，得到二者相关关系(6)

(5)

(6)

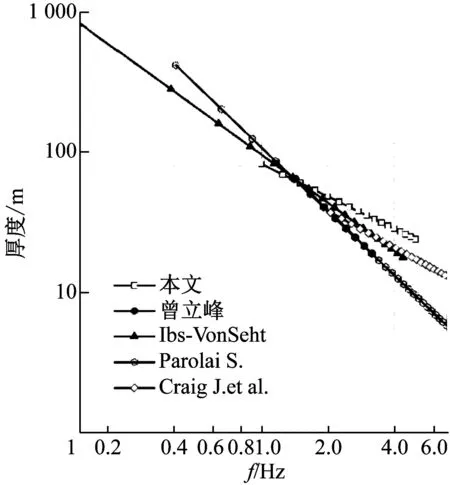
表2中给出了本文地脉动卓越频率与覆盖层厚度拟合公式统计分析结果，图8(a)给出了其拟合曲线。相关性分析显示，a值的标准差为4.07，b值的标准差为0.145，拟合幂函数相关系数R2值为0.595 5>r(34-2)0.001=0.554 1(相关系数临界表)，结果表明，地脉动卓越频率与覆盖层厚度之间的相关性较强，拟合程度较高。

来自不同国家和地区的研究者们，根据各自收集到的钻孔资料和测得的地脉动数据，给出了不同的拟合公式(见表2)。图8(b)给出了不同研究者的拟合结果。由于不同的研究者研究的场地的不同，其所测得的场地地脉动卓越频率的范围也不同。

对比本文和曾立峰的研究结果，在相同覆盖层厚度定义的条件下，拟合结果2～4 Hz区间内相差较大；而对比曾立峰和Parolai的研究结果，虽然两者对于基岩剪切波速的定义不同，但是两者的拟合结果在1～4 Hz区间内十分接近，由此可见，对于不同地区的场地地脉动卓越频率与覆盖层厚度具体的拟合关系式，应做具体研究，不可一概而论。

另外，不同的研究者给出的拟合关系式不同的原因，也可能与其在进行拟合时采用的地脉动卓越频率范围、场地覆盖层厚度范围和观测的场地个数不同有关。表3给出了不同研究者在拟合关系式时所用的地脉动卓越频率范围和覆盖层厚度范围，图9给出了不同研究者观测的地脉动卓越频率分布情况。图10给出了不同研究者的结果相对于Ibs-VonSeht的结果的误差随卓越频率分布情况。

(a)

(b)

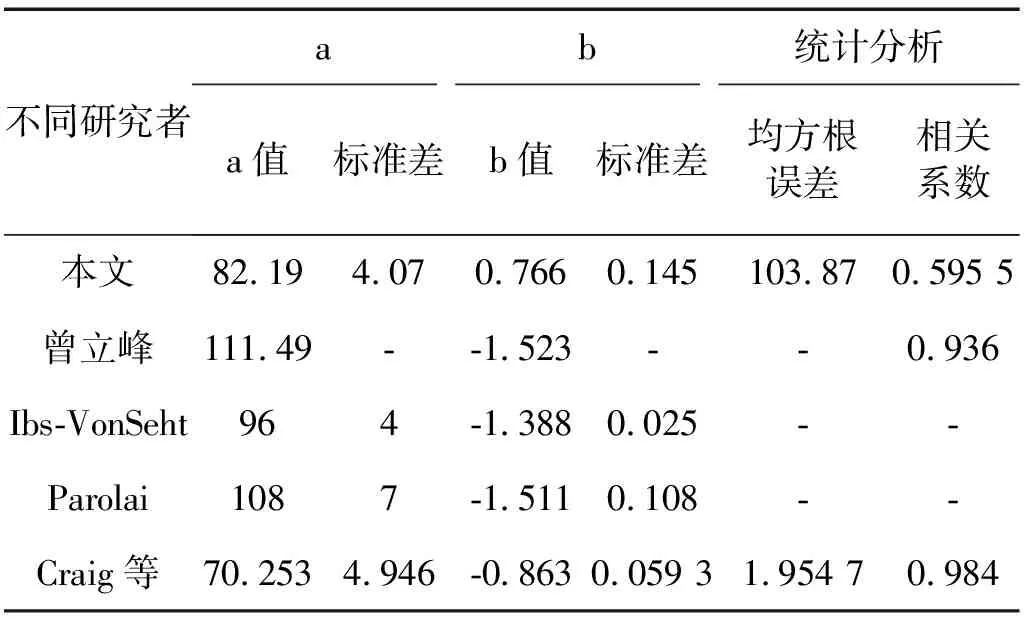
不同研究者ab统计分析a值标准差b值标准差均方根误差相关系数本文82.194.070.7660.145103.870.595 5曾立峰111.49--1.523--0.936Ibs-VonSeht964-1.3880.025--Parolai1087-1.5110.108--Craig等70.2534.946-0.8630.059 31.954 70.984

在0～1 Hz频率区间，仅有Parolai和Ibs-VonSeht的数据点分布在内。Ibs-VonSeht研究是区域为德国下莱茵湾地区的亚琛和埃克伦茨地区，在地理空间上与Parolai研究的科隆地区十分接近。Parolai观测得到的场地最低卓越频率为0.41 Hz，在该频率处也是两者推测厚度相差最大处，相对于Ibs-VonSeht的结果，相差100 m，相对误差为45%；厚度相差最小处在1 Hz位置，相差12 m，相对误差为12.5%；随着卓越频率的降低，误差逐渐增大。

在1～2 Hz频率区间，相对于Ibs-VonSeht的结果，本文和Parolai的拟合结果，在1 Hz处，覆盖层厚度推测相差最大，分别为13.81 m和12 m，相对误差为14.38%和12.5%；在1.3～1.6 Hz之间，本文、曾立峰和Parolai与Ibs-VonSeht的结果十分接近，各个拟合曲线在该区间内相交；在2 Hz处，本文、曾立峰和Parolai的厚度推测结果与Ibs-VonSeht的结果相差分别为4.7 m、5.7 m和5 m，相对误差分别为10.8%、13.1%和11.6%。由图7可知，本文和其他几位研究者的拟合结果在1～2 Hz频率区间内，拟合结果相差不大。

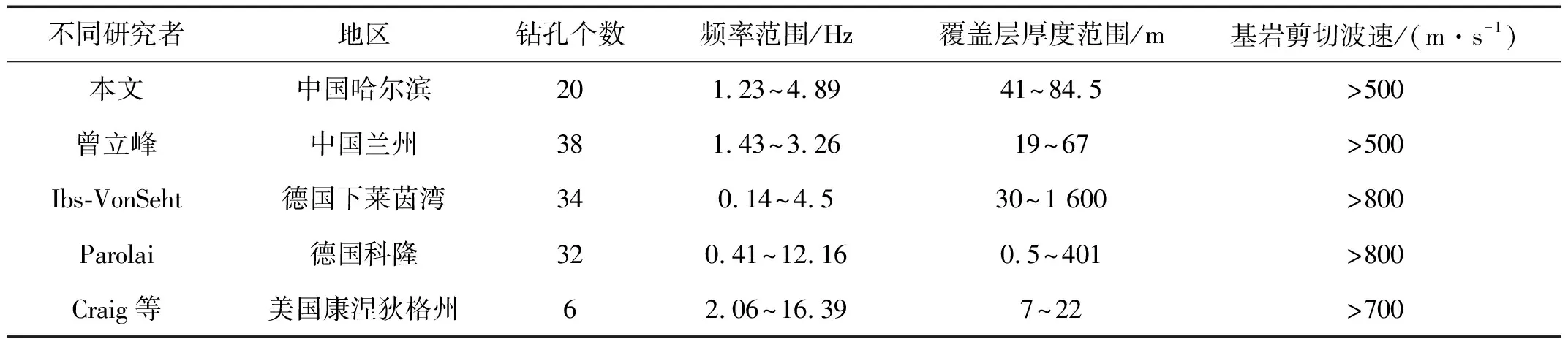
表3 不同研究者拟合时地脉动卓越频率和覆盖层厚度范围值

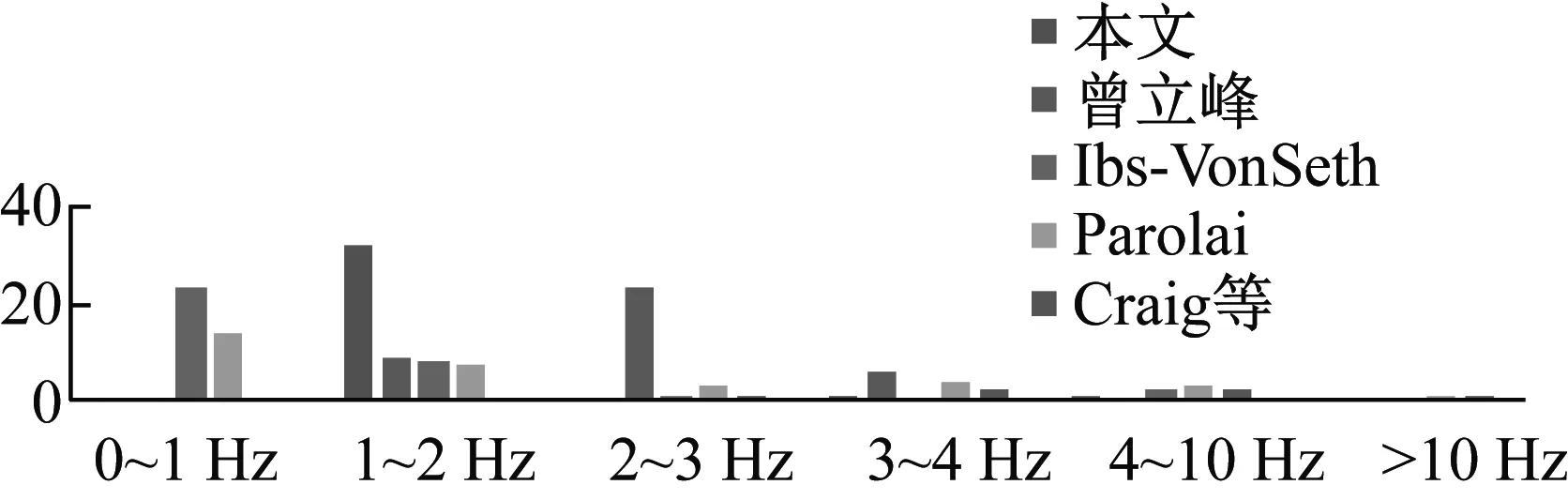
图9 不同研究者测得场地脉动卓越频率分布

在2～4 Hz频率区间，Craig等与Ibs-VonSeht的相对误差较小，但是Craig等仅用了六个场地的地脉动卓越频率来拟合公式，因此其结果随机误差较大；本文、曾立峰和Parolai的结果与Ibs-VonSeht的相对误差随频率的增大而增大，相对误差最小处位于2 Hz处。本文所测的地脉动卓越频率在2～4 Hz区间内，仅有两个数据点，因此本文拟合的公式在该区间内的可靠性较低。而曾立峰和Parolai在该区间内的数据点较多，其拟合结果较为可信。

不同的研究者所得的地脉动卓越频率与场地覆盖层厚度之间的拟合公式，在1～2 Hz内的推测值相差不大，相对误差在15%以下，在0～1 Hz区间，相对误差随频率的减小而增大，在2～4 Hz区间，相对误差随频率的增大而增大。

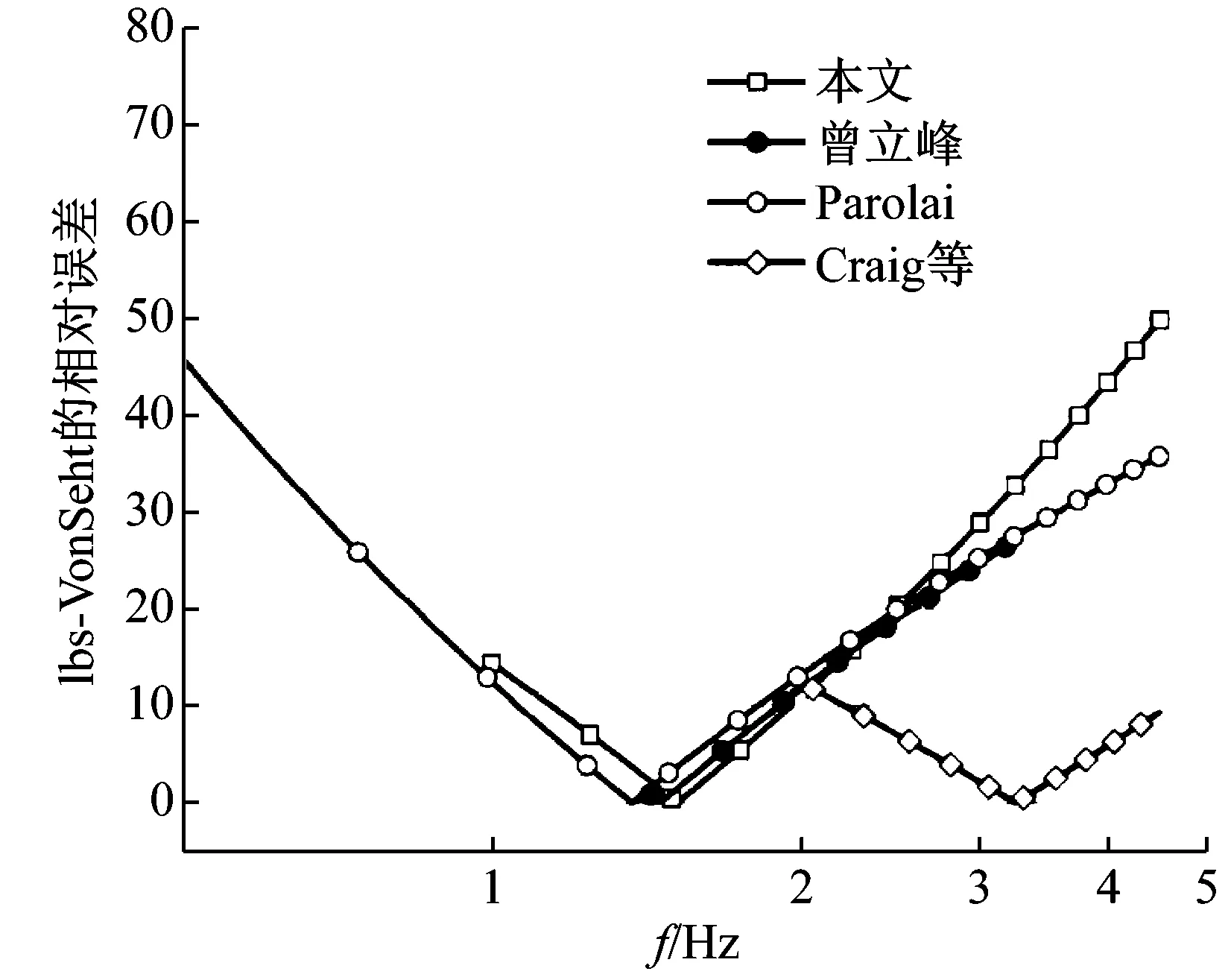
图10 不同研究者拟合结果相对于Ibs-VonSeht的误差分布

3.2 地脉动卓越频率与场地等效周期

场地等效周期的计算公式如下

(7)

(8)

将式(8)代入式(7)得

(9)

式中:di为第i层土层厚度，vsi为第i层土层剪切波速。

根据收集到的钻孔资料，计算各个场地的等效周期Ts、Ts20和Ts30，并结合前文计算得到的场地地脉动卓越频率，采用式(5)幂指数形式进行拟合，得到拟合公式

(10)

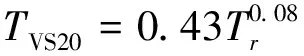
(11)

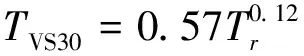
(12)

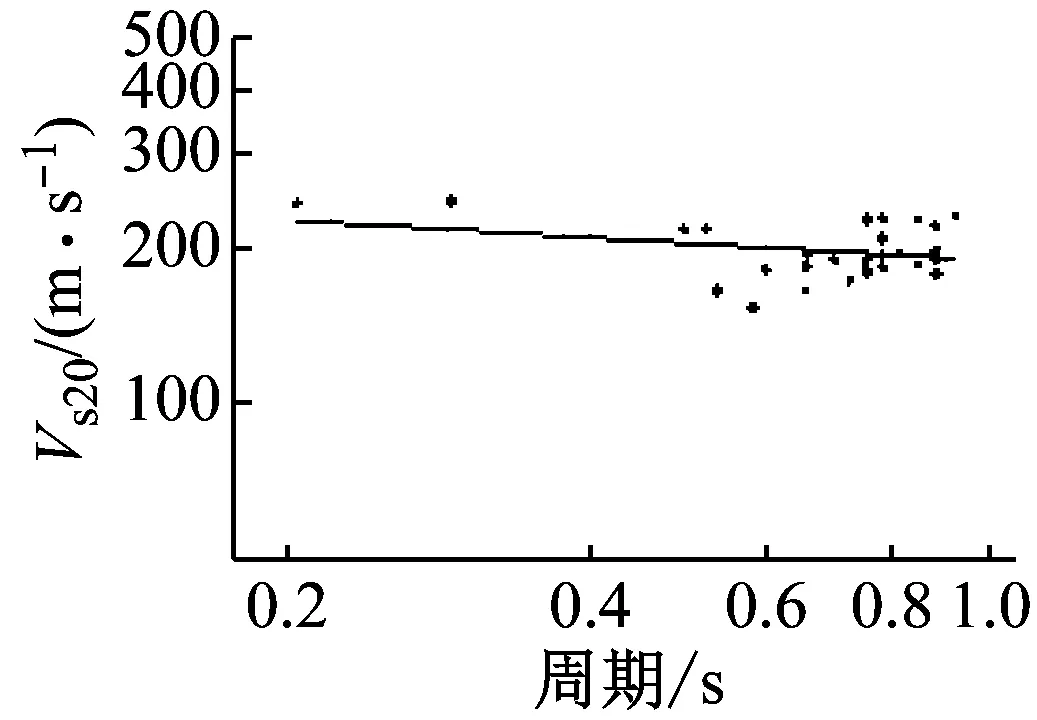
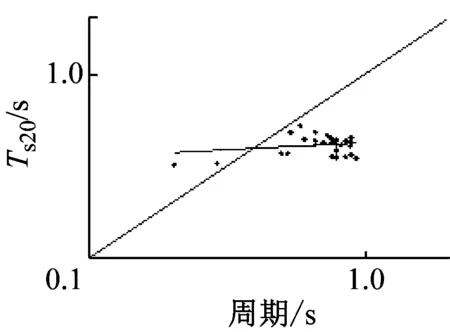
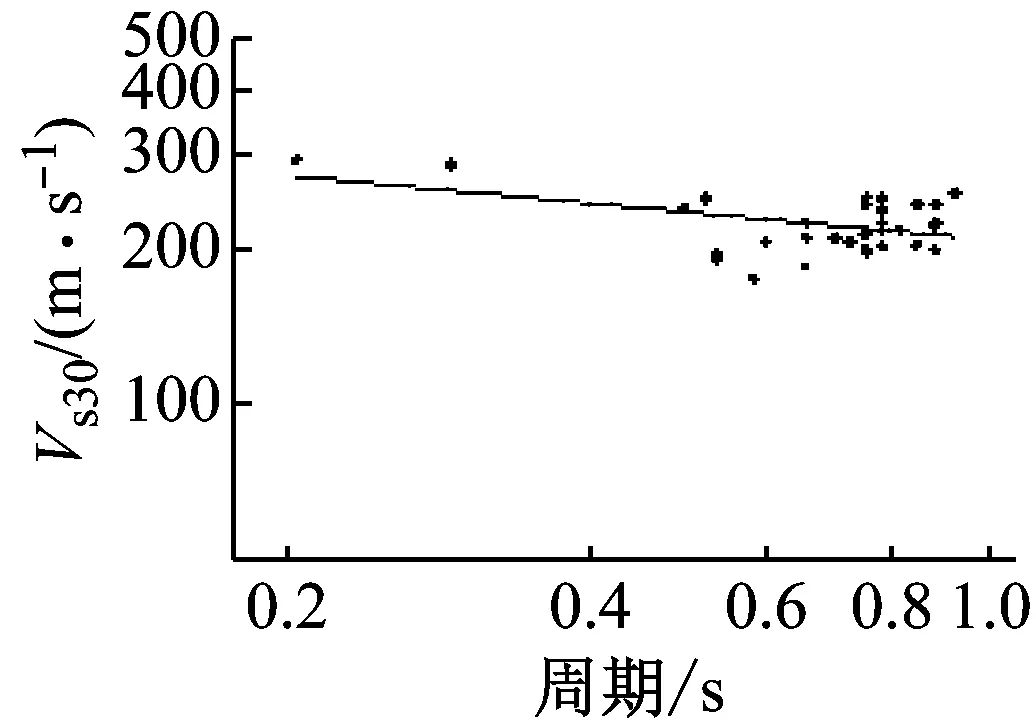
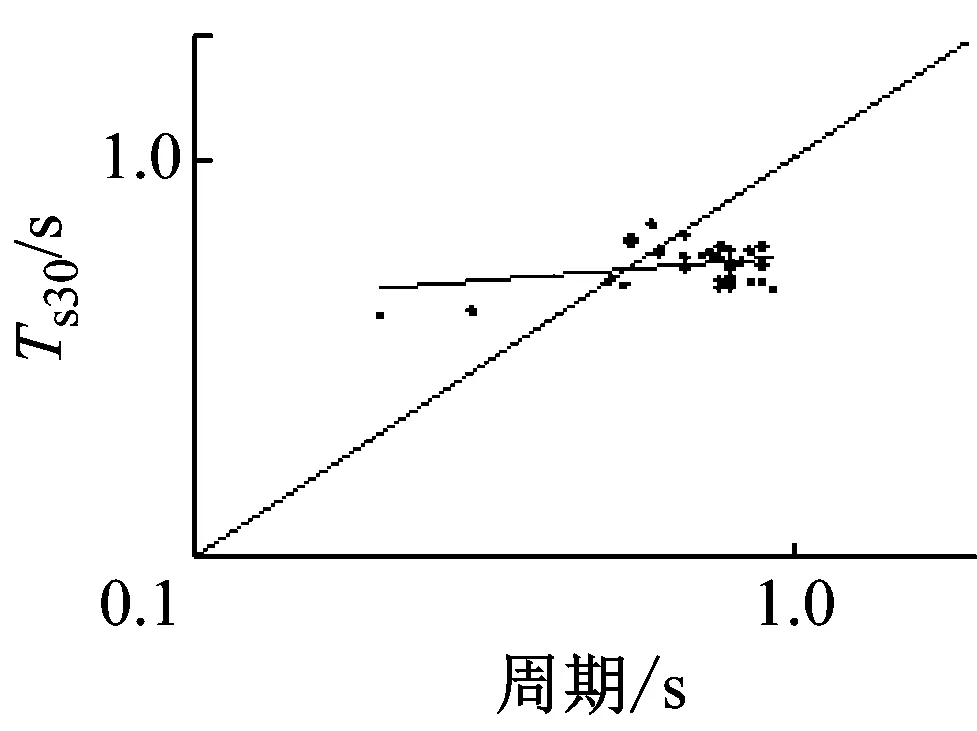
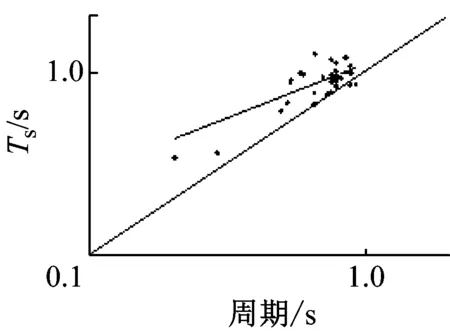
表4给出了地脉动卓越周期与场地等效周期和等效剪切波速的拟合公式统计分析结果，对于拟合公式(10)，其相关系数R2=0.492>r(34-2)0.01=0.448 7，则表明两者中等相关程度，拟合度中等，拟合曲线见图11(f)。对于式(11)和(12)，其相关系数均小于0.1，表明地脉动卓越周期与Ts20和Ts20没有明显的相关性，并且Ts20和Ts30比地脉动卓越周期偏小，见图8(b)、(d)；而Ts比地脉动卓越周期偏大，见图11(f)。整体上看，地脉动单点H/V卓越周期与覆盖层总体的等效周期Ts更一致，略低。

3.3 地脉动卓越频率与场地等效剪切波速

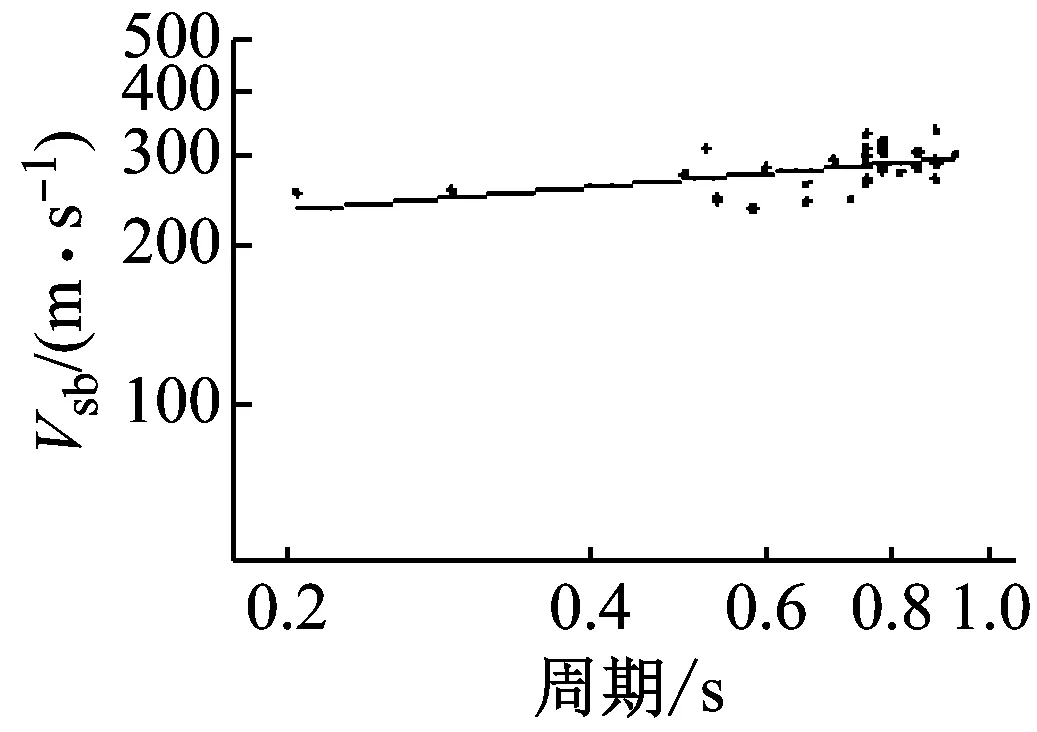
由图11左可以看出，在地脉动单点谱比卓越周期大于0.5 s的32个场地，等效剪切波速Vs20、Vs30和Vsb差别微小，Vs20平均在200 m/s左右，Vs30平均在240左右。Hassani(2016)利用美国NGA地震动数据研究指出了，地震动的单点谱比卓越频率小于2 Hz时，阻抗比小于0.02的场地Vs30均保持在250 m/s左右[14]。本文地脉动研究结果与这一结论是非常一致的，为了便利Vs30也近似采用250 m/s。

同时为了对照，本文也按照式(5)的幂指数形式拟合了地脉动卓越周期与场地Vs20、Vs30和Vsb之间的拟合关系，见式(13)～(15)。

(13)

(14)

(15)

由表3中的相关系数可知，相对来讲，与Vs30和Vsb的相关性要大一些。

表4本文地脉动H/V卓越周期与场地等效周期及等效剪切波速之间拟合公式统计分析

Tab.4ThestatisticparametersoffittingformulasbetweenmicrotremorsH/Vpredominantperiodandsiteequivalentperiods,equivalentshearwavevelocities

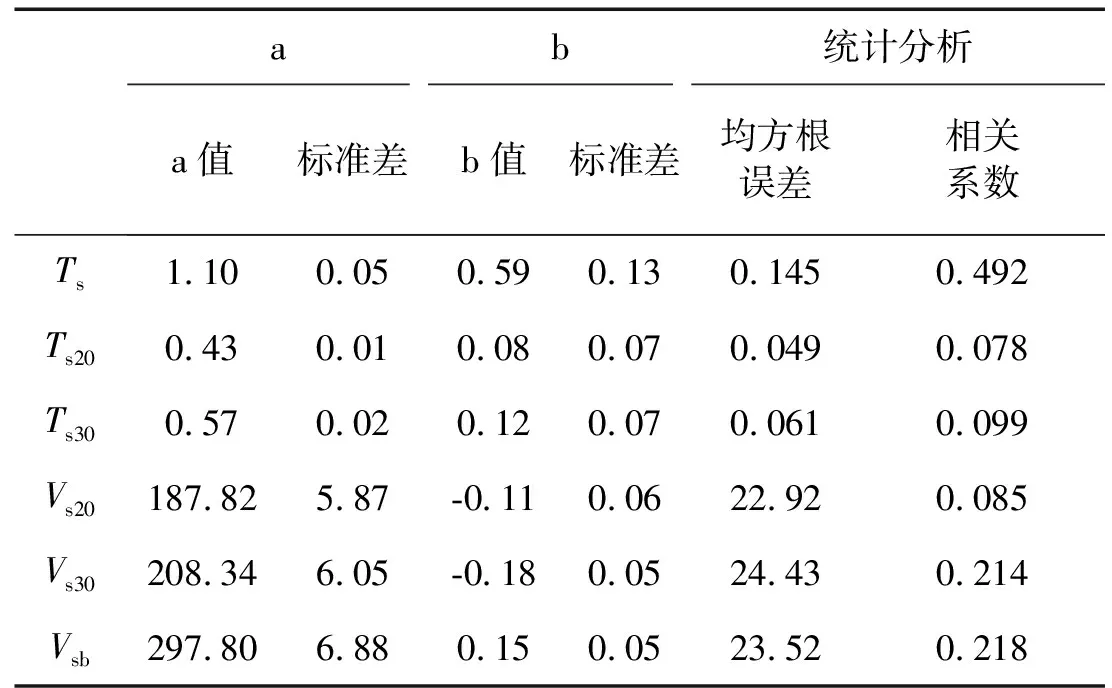
ab统计分析a值标准差b值标准差均方根误差相关系数Ts1.100.050.590.130.1450.492Ts200.430.010.080.070.0490.078Ts300.570.020.120.070.0610.099Vs20187.825.87-0.110.0622.920.085Vs30208.346.05-0.180.0524.430.214Vsb297.806.880.150.0523.520.218

4 结 论

本文观测了37个场地的地脉动，计算分析得到了34个场地的地脉动H/V卓越频率。对这34个场地的地脉动卓越频率与场地特征参数进行幂指数拟合，得到了拟合关系。分析结果显示，地脉动H/V卓越周期与场地覆盖层厚度之间存在明显的相关性，与覆盖层等效周期Ts大体相当，地脉动H/V谱比卓越周期大于0.5 s时，场地的等效剪切波速Vs20和Vs30以及等效周期Ts20和Ts30变化不大，平均分别为200 m/s，250 m/s，0.8 s和0.6 s。

利用地脉动H/V谱比法的卓越频率可以快速测定场地覆盖层厚度和特征周期Ts等特征参数。在1～2 Hz频带区间内，不同地区估计的覆盖层厚度相对误差小于14.38%；但是在0～1 Hz区间，相对误差随频率的减小而增大，在2～4 Hz区间，相对误差随频率的增大而增大。主要原因是在这频带对应场地地脉动观测数据相对较少，通过在更多地区不同类型场地地脉动观测数据和研究成果的积累，测定精度有望进一步提高。

(a)

(b)

(c)

(d)

(e)

(f)