基于附加虚拟质量的储罐损伤识别方法

侯吉林， 景天雨， 王鹏飞， 张青霞， JANKOWSKI ukasz

(1. 大连理工大学 土木工程学院， 辽宁 大连 116023; 2. 大连理工大学 海岸和近海工程国家重点实验室， 辽宁 大连 116023; 3. 大连民族大学 土木工程学院， 辽宁 大连 116600; 4. 波兰科学院基础技术研究所智能技术部， 华沙 波兰 02-106)

随着我国石油化工的发展以及国家的石油战略储备计划[1]的实施，服役和兴建的储罐会越来越多，然而这些储罐一旦发生工程事故，将会对人民生命财产造成很大的损失，因此，对现役储罐的监测受到越来越多的关注。目前，储罐的检测方法主要有射线检测法、声发射检测法[2]、超声波检测法等、漏磁检测法[3]、涡流检测法[4]等。这些方法的优点是不依赖于结构有限元模型，但往往不能定量的评估损伤程度。近年来,基于振动测试的损伤识别技术得到了广泛的发展和应用[5],选择一个合适的损伤指标非常重要[6]。结构模态是结构物理参数的特征函数，结构物理参数的变化必然导致结构模态参数的变化[7]，因此模态被广泛应用于结构的损伤识别。许成祥等[8]基于试验模态分析的基本原理, 完成了对立式拱顶钢制原油储罐模型的应变模态试验。楚孝田[9]根据模态分析技术的原理，结合大型原油储罐振动特性，提出用模态分析技术来对储罐损伤进行检测的方法。然而实际的储罐形状往往是圆柱型，结构环向对称，模态密集，且同一高度的不同位置的损伤可能引起的模态改变是相同的，这些都为储罐结构的损伤识别增加了困难。

杨秋伟等[10]在原结构某些位置附加已知的集中质量，杨志春等[11]在原结构上添加刚度系数已知的刚度元件，形成新的参考结构，然后测试参考结构的频率信息，联合原结构和参考结构的频率信息识别损伤参数。周卫东等[12]通过在结构的某些部位附加已知的集中质量元件，利用广义柔度灵敏度矩阵建立了损伤识别方程。Holnicki-Szulc[13]提出了虚拟变形法( Virtual Distortion Method，VDM)，利用虚拟变形法来模拟结构发生的损伤，可以有效的识别结构发生的损伤。Suwala等[14]通过 VDM 法在无模型条件下进行了质量识别。张青霞等[15]通过VDM法识别了车-桥耦合系统的移动质量。Hou等[16]通过VDM法在平面框架结构上附加虚拟质量，利用数值模拟验证了方法的有效性。本文利用附加物理参数增加了测试频率数据量的思想，来提高储罐结构损伤识别的精度。并进一步结合虚拟变形法(VDM)的基本思想，通过附加虚拟质量代替附加实际质量，提高方法应用的灵活性。基于虚拟变形法，只需测量一组激励和一组加速度响应，即可数值地构造出附加虚拟质量后结构的频率响应，可避免在实际工程中附加真实质量所面临的一些困难，降低了实际操作的难度[17]。

本文首先介绍如何利用虚拟变形法附加虚拟质量，然后基于附加虚拟质量的子结构模态信息初步判断损伤位置，之后基于灵敏度推导子结构附加虚拟质量的损伤识别公式，最后通过储罐模型验证方法的有效性。

1 附加质量的储罐损伤识别方法

1.1 附加虚拟质量

根据VDM法的基本思想，通过一组激励和一组加速度响应可以数值地构造出附加虚拟质量m后结构的频率响应[18]，实现在原结构上附加虚拟质量。构造的公式为

(1)

式中：Hpp(ω,m)表示结构在p自由度方向附加虚拟质量m后对应该自由度方向的加速度频率响应；F(ω)和A(ω)分别表示原结构在p自由度方向上的激励和加速度的频域响应；m是p自由度方向上附加的虚拟质量。利用构造的频率响应识别出频率，作为损伤判断的依据。

下面利用单自由度系统(如图1)，对基于虚拟变形法构造虚拟质量的操作方法进行介绍。

图1 单自由度系统

如图1质量、刚度和阻尼为M，K和C。在荷载F(ω)的作用下，其加速度响应A(ω)为

(2)

设M=1、K=2和C=1，ω=1,F(ω)=2,则对应A(ω)=-1+i，对应的频率响应h(ω)=-0.5+0.5i。下面分别利用式(2)和(1)计算增加质量m=0.5后的频率响应。

(1) 直接法，若在质量增加m=0.5，则将M=1.5代入式(2),得到A1=-0.8+1.6i，对应的频率响应h1(ω)=-0.4+0.8i。

(2) 虚拟变形法，将m=0.5，A(ω)=1，F(ω)=2代入式(1),可以得hm(ω)=-0.4+0.8i。

两种方法得到的频率响应相同h1(ω)=hm(ω)，验证了方法的正确性。

1.2 损伤位置的初步定位

一般储罐为圆柱型，相同高度位置环向壁厚相同。利用这个结构特点，通过环向比较附加质量后的频率，可以初步判断损伤的位置和程度。

图2 子结构划分示意图

(3)

(4)

1.3 基于灵敏度的损伤识别

如果利用上述方法初步判断储罐存在损伤，则可以结合有限元模型进行损伤程度的识别。

将获得的虚拟结构的模态称为试验模态，储罐有限元模型上附加相同虚拟质量后对应的模态称为理论模态。把理论模态与试验模态之间的误差范数作为目标函数，通过优化子结构参数使目标函数最小，实现损伤优化识别。构造目标函数T(μ)，见式(5)，为了方便表示，将上节中的按照空间位置排列的频率矩阵，排列为一个列向量。优化方法选取牛顿法。

(5)

式中：Δωi(μ,m)为损伤因子为μ，子结构i附加虚拟质量m时理论模态ωi(μ,m)与试验模态ωA,i(m)之间的相对误差。损伤因子为损伤前后的刚度的比值。计算公式如式(6)

(6)

对T(μ)分别求一阶导和二阶导可以得到

(7)

(8)

这里，Δω(μ,m)是所有子结构试验和理论模态的相对误差的向量形式，P是Δω(μ,m)相对于μ的Jacobi矩阵。我们将P定义为灵敏度矩阵，P，Δω(μ,m)和μ按照式(8)构造

(9)

(10)

(11)

将式(7)和式(8)代入式(11)，整理可以得到

μ=μ0+P+Δω(μ,m)

(12)

式中：P+表示P的广义逆，可由奇异值分解计算。损伤因子μ可以由式(12)近似求出，然后将求得的μ作为下一步迭代的初始值μ0，利用新的结构参数构造新的灵敏度矩阵P，重复上面的步骤进行迭代，直到收敛。

2 油罐模型算例

下面通过油罐模型的数值仿真，来介绍和验证附加虚拟质量方法的有效性。

2.1 建立油罐理论有限元模型

2.1.1 模型基本信息

模型采用钢制立式圆罐形固定顶储罐(标准序号HG 21502.1-92-208)，直径7 500 mm，罐壁高度7 500 mm，拱顶高度805 mm，总高度8 305 mm，罐壁厚度6 mm，底板厚6 mm，拱顶板厚5.5 mm。罐壁和底座连接处进行焊接。底板固定在地面上。罐体材料为钢，弹性模量2.1 Gpa，密度7 850 kg/m3，泊松比0.3。

建立ANSYS有限元模型(如图3)，罐壁、底板和罐顶均采用shell63单元。网格划分时，采用二维映射划分，罐壁划分320个单元，罐底划分192个单元，罐顶划分192个单元，总共704个单元。罐壁每四个单元为一个子结构。

图3 储罐结构

2.1.2 模态分析

表1 模型的前5阶频率

第1阶阵型第2阶阵型

第3阶阵型第4阶阵型

图4 前4阶阵型

Fig.4 The first 4 mode

通过ANSYS计算得到储罐模型的前5阶频率(见表1)和前4阶阵型(见图4)。由于储罐结构属于对称的空间结构，会出现重频率并且各频率比较接近。为了方便结构参数的优化和运算，利用ANSYS导出刚度矩阵和质量矩阵，然后采用MATLAB进行计算。

2.2 损伤识别

本节模拟小锤激励计算加速度响应，利用加速度响应识别对应质量下的结构频率，然后通过灵敏度的方法进行损伤识别。

2.2.1 损伤模型

如图5，选择储罐罐壁三分之一区域为待识别区域，划分为25个子结构，子结构编号用SV,H表示，其中V和H分别代表子结构在原结构中的竖直位置和水平位置。

图5 储罐结构

2.2.2 激励和响应

利用图 6模拟小锤激励，考虑5%的白噪声，小锤激励的持续的时间是8.8 ms。采样频率为2×104Hz。小锤作用在子结构S3,3的中间位置，计算时间为10 s，考虑5%的白噪声。图 6为子结构S3,3中间位置前50 ms的激励。图 7为子结构S3,3中间位置前0.5 s的加速度响应。

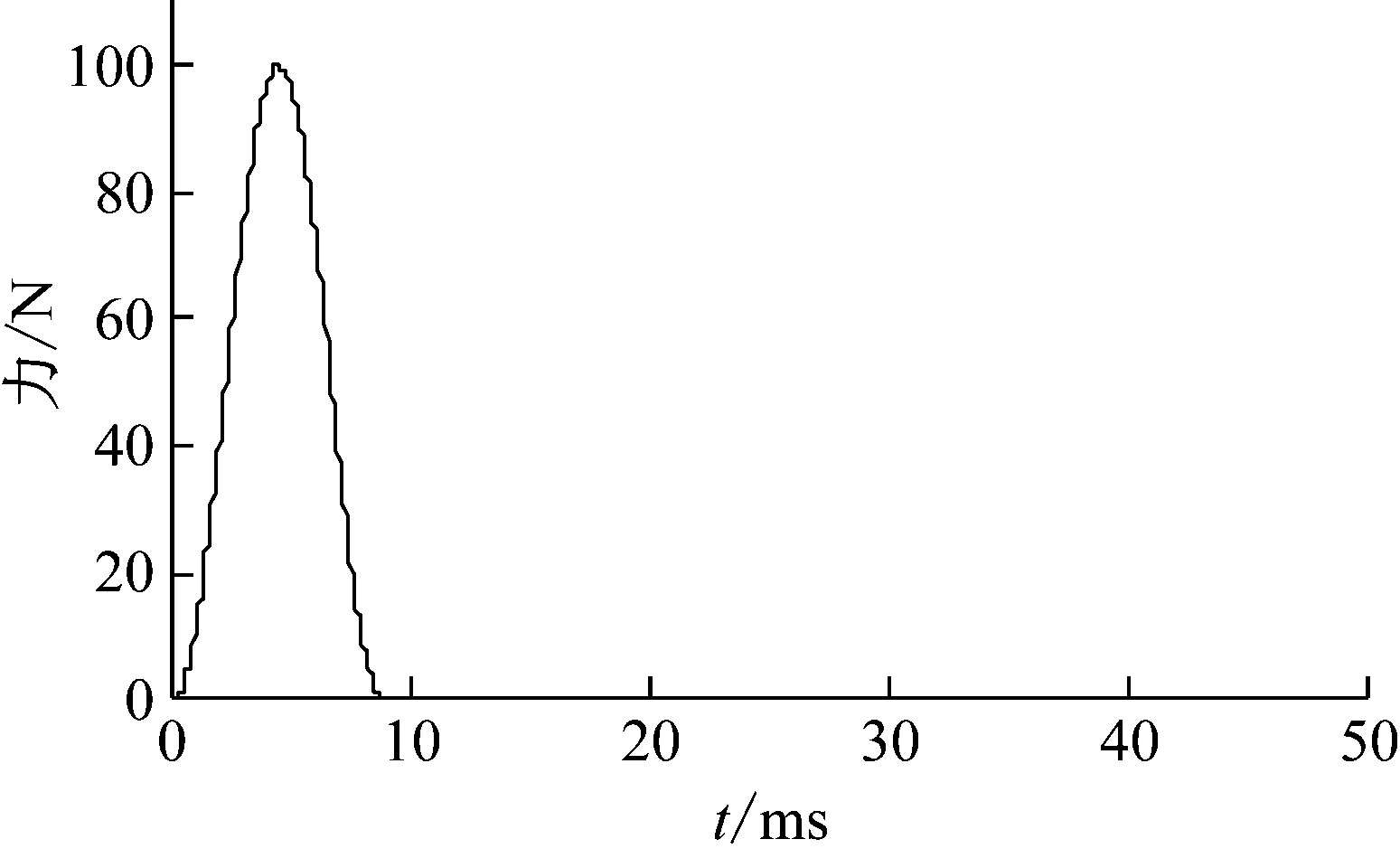
图6 小锤激励

图7 加速度响应

2.2.3 构造虚拟质量

利用理论未损伤模型，在子结构S3,3的中间位置施加垂直于罐壁方向的激励，得到对应的加速度频率响应，其频率响应的幅值见图 8(Original)；在子结构S3,3的中间位置中间附加集中质量200 kg后，利用有限元模型直接计算的频率响应幅值为图 8(FEM)；利用图 8(Original)的频率响应代入式(1)可计算出附加虚拟质量200 kg后的频率响应的幅值，见图 8(VDM)。比较两条曲线，两者完全吻合，说明利用VDM的方法构造附加虚拟质量后的频率响应是完全精确的，而其不需要集装有限元模型，大大提高计算效率。

图8 利用VDM方法构造频率响应

另外，从图8中可以看出，原储罐在激励作用下，多阶低阶模态被激励出来，且比较密集，不利于模态识别和进一步的损伤识别。在附加虚拟质量之后，储罐以单个模态振动为主，易于识别，且通过灵敏度分析可知该模态对损伤具有较高敏感度。

2.2.4 附加虚拟质量与灵敏度关系

首先在子结构S3,3的正中间位置附加虚拟质量m。计算前5阶频率关于子结构S3,3的相对灵敏度变化，见图 9，相对灵敏度的计算公式见式(13)，相对灵敏度为对灵敏度关于频率归一化的结果，有利于各阶灵敏度的比较和分析。由图 9可以看出，第1阶频率随质量的增加相对灵敏度一直在提高；而第2、3、4阶频率的相对灵敏度保持在0.01几乎没有变化，第5阶频率随质量的增加相对灵敏度一直在降低。在其他24个子结构中间附加虚拟质量，构造虚拟结构GV,H(μ,m),i=1,2,…,25,i≠1，综合所有25个子结构GV,H(μ,m)的灵敏度与附加虚拟质量的关系曲线，V=1的虚拟结构G1,H(μ,m)选定第17阶频率，其余各虚拟结构选定第1阶频率。

(13)

图9 附加质量后相对灵敏度与附加质量的关系

2.3 损伤位置的确定

假设储罐结构发生损伤(如图10)，损伤因子见表2。分别在所有25个结构的中间施加如图6所示的小锤激励，计算对应激励位置的加速度响应。利用考虑5%噪声的激励和响应，代入式(1)，分别计算出各子结构附加虚拟质量300 kg后的频率响应的幅值，通过傅里叶变换并进行峰值提取，得到各个虚拟结构所选定的频率。其中V=1时，各虚拟结构选定第17阶频率；V=2,3,4,5时，各虚拟结构选定第1阶频率。然后将各个子结构的频率汇总到表3，计算出每一个子结构的损伤识别系数(图11)。

表2 损伤因子

图10 损伤示意图

表3 频率

图11 损伤识别系数柱状图

从表3看出损伤因子μV,H越小，横向比较对应得到的子结构的频率越低，对应图11的损伤识别系数DV,H越大。在储罐中间区域9个子结构(S2,2～S2,4，S3,2～S3,4，S4,2～S4,4)损伤识别系数相对较大，说明损伤应该在此区域，其中子结构S4,4损伤最大，子结构S3,3次之。

2.4 灵敏度优化方法损伤识别

通过上节的损伤识别系数，找到了储罐结构损伤的大致位置和损伤的大致程度，但是要得到较为精确的结果，需要结合有限元模型，识别结构的损伤因子。为了方便优化，将上一节找到的损伤区域的9个子结构重新编号，编号为1～9。如图12。

上一节我们已经计算出损伤区域每个子结构的附加300 kg虚拟质量后所选定的频率。利用这个结果，通过式(13)计算每个子结构的第一阶频率关于9个子结构的相对灵敏度，并照式(9)组成相对灵敏度矩阵，相对灵敏度矩阵的示意图为图 13。由于这个灵敏度矩阵是对角矩阵，条件数比较好，所以基本上第一次迭代(i=1)就已经比较接近实际损伤因子(actual)了，然后只需迭代2次就能收敛，并能很精确地识别出损伤因子，见图 14。

图12 损伤示意图

图13 相对灵敏度矩阵

图14 识别的损伤因子

2.5 其他位置损伤对识别的影响

为考虑识别区域以外的损伤对识别结果的影响，设置如下工况：如图 15，其中子结构1～9的损伤因子如图14保持不变，为待识别区域；在此区域以外的子结构a和b也存在损伤，其中a的损伤因子为0.6，b的损伤因子为0.6。这里只在子结构1～9上进行操作，包括激励、计算加速度响应(考虑5%噪声)和构造虚拟质量，具体方法同2.3和2.4节。利用在这9个子结构上附加虚拟质量后的频率识别的损伤因子如图 16。由图16可知，除了第6个子结构，其余的识别误差在5%以内，满足要求。子结构6出现较大误判是由于子结构a存在损伤且离其太近，子结构a的损伤对斜向相邻的子结构3和9影响就很小了；而子结构b距离识别区域较远，其损伤对识别结果的影响可以忽略不计。

图15 损伤示意图

图16 识别的损伤因子

3 结 论

针对储罐的具有空间对称、低阶模态密集且对局部损伤不敏感的特点，提出基于附加虚拟质量的损伤识别方法，并利用储罐有限元模型验证了方法的有效性，得到了以下结论：

(1) 通过在储罐上附加虚拟质量，改变模态分布特点，使其具有对局部损伤灵敏度较高的频率信息，并提高了测试模态数据量。

(2) 基于虚拟变形法(VDM)的基本思想，利用原结构的激励和加速度响应构造附加任意质量后的频率响应，进一步增加了方法的灵活性和应用性。

(3) 该方法分为两步，首先通过附加虚拟质量后的频率可快速初步判断损伤的位置，然后结合储罐的有限元模型，利用灵敏度矩阵快速识别储罐的损伤程度。