黏弹性阻尼器减震结构基于位移减震域的设计方法

刘文光， 阎美智， 于维欣， 何文福

(上海大学 土木工程系， 上海 200072)

随着建筑物的高度和跨度不断增加，体型越来越复杂，结构抗震分析与设计难度也随之不断增加。复杂而不规则的高层结构体系，在地震作用下，薄弱部位产生损伤甚至失效，引起结构的严重破坏[1]。消能减震作为一种应对地震灾害的技术，通过采用附加子结构或一定的措施，以消耗地震传递给结构的能量为目的的减震手段[2]。黏弹性阻尼器是常用的速度型阻尼器，主要利用其中的黏弹性材料发生剪切变形来耗散振动能，增加结构的阻尼，从而达到减小结构动力反应的目的。目前阻尼器在工程中已得到较为广泛的应用，但是尚没有形成统一的设计方法，其布置方式依赖于工程经验，进行反复的预估及试算，过程十分繁琐，需要占用大量的时间和资源，且其计算结果通常过于保守。因此，进行消能减震体系阻尼器设计方法的研究，探究阻尼器对结构动力响应的影响是十分必要的。

Shukla等[3]提出黏弹性阻尼器的三种不同力学模型配以三种不同的布置方式以进行阻尼器的优化布置。Takewaki[4]以层间位移的均方差之和作为目标函数，并用临界激励法对目标函数进行简化设计。Lopez-Garcia[5]用一种简化顺序搜索算法控制黏滞阻尼器数量，对减震结构进行优化布置。Singh等[6]以结构响应函数为目标函数，利用遗传算法确定黏弹和黏滞阻尼器的位置及参数。滕军等[7]以线性系统的二次型性能指标作为目标函数，研究了高层结构控制装置数量、位置和参数的优化设计方法。Lin等[8]提出被动耗能体系基于位移的抗震设计方法，编制线性迭代法程序用于预测规则减震结构耗能特性。Lee等[9]利用结构特征值理论对结构固有频率以及黏弹性阻尼器的参数及布置进行优化，并将此方法应用于十层剪切框架阻尼器优化布置。常业军等[10]利用反应谱法探讨结构阻尼比及刚度对地震反应的影响，并结合工程实例提出黏弹性阻尼器的减震设计方法。张思海等[11]基于能力谱法简化计算速度相关型阻尼器的等效阻尼比，通过调整阻尼器的数量及参数以满足结构性能水平。 Aydin等[12]采用振幅基底剪力传递函数以及最大位移传递函数作为目标优化函数，对阻尼器参数进行优化。曲激婷等[13]提出一种黏弹性阻尼器的新型优化数学模型，对阻尼器最优布置下的结构反应进行分析研究。Fujita等[14]基于梯度渐进优化方法，以控制结构的楼层加速度以及层间位移为目标函数，确定黏弹性阻尼器的最优布置方式。闫维明等[15]将铅剪切阻尼器应用于高层剪力墙结构，通过多次试算得到了阻尼器的优化布置方式。吴从晓等[16]提出高位转换黏滞阻尼减震结构的合理黏滞阻尼系数计算方法，控制转换层上部剪力墙数量以实现更好减震效果。翁大根等[17]提出一种针对附加黏滞阻尼器减震结构的实用设计方法，列出消能部件方案设计及性能参数配置的计算公式。林绍明等[18]采用积算公式和减震层阻尼力比公式对减震层的位置、数量和阻尼器参数进行优化分析。苏毅等[19]根据消能器耗散的能量与结构的总应变能两者比值，估算出结构消能器的数量并进行优化设计。Sanchez等[20]利用增量逆分析法重新设计黏滞阻尼结构得到目标传递函数，优化阻尼器布置位置及附加阻尼系数。

上述研究多数采用目标函数或算法优化等方法对黏弹性阻尼器参数及布置进行研究，然而并未就黏弹性阻尼器对结构的减震影响范围做出进一步分析，且其减震设计方法繁琐复杂，工程上难以简单快速进行设计。本文对附加黏弹性阻尼器的减震结构进行减震影响域分析研究，通过大量时程分析计算结果进行曲线回归推导经验公式，提出了一种黏弹性阻尼器减震结构基于位移减震域的设计方法，可用于快速评价减震结构的动力响应。

1 结构层间位移减震域理论分析

本文的黏弹性阻尼器采用等效刚度和等效阻尼模型，该模型简单且应用范围较广，黏弹性阻尼器的滞回曲线如图1所示，其恢复力模型可以表示为

(1)

图1 黏弹性阻尼器滞回曲线

装有黏弹性阻尼器的多自由度结构的运动方程为

(2)

式(2)中

(3)

式中：[Cd]和[Kd]分别为阻尼杆件提供的附加阻尼矩阵和刚度矩阵，由其单元阻尼矩阵集成得到。

将式(3)代入式(2)整理得

([K]+[Kd]){u}={P}

(4)

(5)

由式(5)可得布置黏弹性阻尼器的减震结构振型，阻尼器的等效刚度一定程度上影响结构振型，振型对比如图2所示。

图2 原结构与减震结构前三阶振型对比示意图

Fig.2 Modes comparison of original structure and damper-added structure

由于减震结构的阻尼不影响结构振型，且属于非经典阻尼矩阵，不易于进行振型分解求解，无法快速预测减震结构的地震响应。本文提出减震域的概念，定义为黏弹性阻尼器对于整体结构中所有相应楼层响应的减震影响范围。减震域通过层间位移比表示，其计算公式由减震前后的层间位移减震比γ得到，如式(6)所示

(6)

2 黏弹性阻尼器结构层间位移减震域分析

2.1 结构模型及分析工况

为了探讨黏弹性阻尼器减震结构层间位移减震域共性影响，本文采用MATLAB建立多层标准框架结构(层高及刚度每层均相同)为计算对象并进行纽马克非线性分析计算，分析9层、15层、19层、23层、29层标准框架结构，简化计算模型及阻尼器布置示意图如图3所示，附加黏弹性阻尼器位置如表1所示。单个黏弹性阻尼器参数设定为刚度Kd=0.02K与阻尼系数Cd=1.1C，其中K为原结构层刚度，C由原结构Rayleigh阻尼矩阵计算得到。

减震设计按规范设计，因此时程分析的地震波选用7条地震波，其中包括2条人工波，5条天然波，分别为RH2、RH4、TFEW、TJEW、CPC、ELNS、HANS，对结构进行非线性动力时程反应分析，7条地震波计算所得结构底部剪力结构满足《建筑抗震规范》(GB 50011—2010)，其平均反应谱曲线与规范谱曲线在统计意义上相符，如图4所示。

图3 模型及阻尼器布置示意图

图4 地震波的地震影响系数曲线

结构层数N阻尼器设置位置1/3N1/2N2/3N单因素Kd单因素Cd单因素Kd单因素Cd单因素Kd单因素Cd9D(Kd)9-3-nD(Cd)9-3-nD(Kd)9-5-nD(Cd)9-5-nD(Kd)9-6-nD(Cd)9-6-n15D(Kd)15-5-nD(Cd)15-5-nD(Kd)15-8-nD(Cd)15-8-nD(Kd)15-10-nD(Cd)15-10-n19D(Kd)19-6-nD(Cd)19-6-nD(Kd)19-10-nD(Cd)19-10-nD(Kd)19-12-nD(Cd)19-12-n23D(Kd)23-8-nD(Cd)23-8-nD(Kd)23-12-nD(Cd)23-12-nD(Kd)23-16-nD(Cd)23-16-n29D(Kd)29-10-nD(Cd)29-10-nD(Kd)29-15-nD(Cd)29-15-nD(Kd)29-20-nD(Cd)29-20-n注:D(Kd)N-m-n中,N为结构楼层总数,m为阻尼器布置层位置,n为阻尼器布置个数

2.2 层间位移减震域结果影响分析

2.2.1 阻尼器单因素Kd层间位移减震域分析

图5为阻尼器单因素Kd影响工况的时程分析结果，从结果可知阻尼器参数Kd对楼层减震影响域主要体现在布置层，另外不同阻尼器楼层布置的对本层的位移减震比一致，即楼层层数对布置层的减震比基本无影响。图6为不同Kd值对本层位移减震比的影响关系图，可得到阻尼器布置层刚度比与减震比成线性关系。

2.2.2 阻尼器单因素Cd层间位移减震域分析

图7为阻尼器单因素Cd影响工况的时程分析结果，从结果可知阻尼系数Cd对楼层减震影响主要体现在布置层，同时会不同程度地影响到相邻层，阻尼器布置层以上的减震效果比布置层以下的效果明显；布置层的减震比随着楼层层数的增加而减小，且随着阻尼器个数的增加，减震域越大。

图5 参数Kd对层间位移减震效果对比图

图6 阻尼器布置层刚度比与减震比关系

图7 参数Cd对层间位移减震效果对比图

2.2.3 阻尼器位置层间位移减震域分析

图8为阻尼器设置在不同楼层对本层层间位移减震比的影响，阻尼器参数设定为1Cd、4Cd及6Cd。阻尼器设置位置对布置层的减震比影响较小，故可不考虑相邻层的结构参数对布置层减震比的影响。

图8 阻尼器设置位置与γCdi关系

3 层间位移减震域简化预测理论

3.1 γKd减震域预测公式

由层间位移减震域分析结果，附加刚度Kd主要对阻尼器布置层产生作用，其减震域表达式可由式(7)得到

(7)

简化计算模型如图9所示。故γKd减震域理论公式为

(8)

式中：γKdi为第i层的层间位移减震比；Ki为第i层结构楼层刚度；Kdi为阻尼器布置层的总刚度，即Kdi=Kd+Ki。

图9 γKd减震域简化计算模型

图10为γKd时程分析结果与理论结果对比图，两者基本吻合。

3.2 γCd减震域预测公式

图10 γKd时程分析结果与理论结果对比

由层间位移减震域分析结果，由于阻尼器布置层以上的楼层不存在边界约束，层间位移减震比略大于阻尼器布置层以下的楼层，故γCd减震域函数分三段进行拟合计算。

(1) 阻尼器布置层公式

图11为不同楼层结构λ与γCdi关系，由此得到曲线回归方程

γCdi=0.004 4e-0.13N×λ2-0.17e-0.08Nλ+1

(9)

图11 不同楼层结构λ与γCdi关系

(10)

式中：x为任意楼层与阻尼器布置层的相对位置，x=Ni-Ndi；Ni为结构任意层；Ndi为阻尼器布置层。定义ω为楼层影响系数，ω=-0.015N+0.93；τ为楼层衰减系数，τ=0.19N-1.46。

(11)

β=(1-5×10-4lg(λ)-1×10-3)x

(12)

图12为λ=15时的时程分析结果与拟合结果对比，两者误差均在5%左右。

4 结构层间位移减震域组合分析

4.1 阻尼器单层布置组合

图13 γKd和γCd叠加效果对比

结构层间位移减震指标由γKd和γCd线性组合得到

γ=1-(1-γKd)-(1-γCd)=γKd+γCd-1

(13)

图14为λ=5时，阻尼器单层布置组合的时程分析结果与拟合结果对比，两者吻合。

4.2 阻尼器多层布置组合

在计算模型中任选三层同时布置阻尼器，并得到时程分析结果。图15给出了时程结果与线性叠加结果的对比，两种方法计算结果吻合，因此可认为不同阻尼器布置层对减震结构的动力响应影响可线性叠加。

图14 γKd,Cd时程分析结果与拟合结果对比

图15 不同阻尼器布置层叠加效果对比

多层布置阻尼器时，由于误差累加导致计算结果产生一定的偏差，故在多层布置组合计算时，引入减震比修正系数ζ，因此减震比可按式(14)进行计算

(14)

ζ=0.131 2×max(λ)+0.83

(15)

式中:ζ为减震比修正系数，与位置参数λ有关，且两者成线性关系，如图16所示。

图16 减震比修正系数ζ与位置参数λ关系

图17为λ=1，λ=1.5和λ=2时，阻尼器多层布置组合时的时程分析结果与拟合结果对比图，两者吻合。

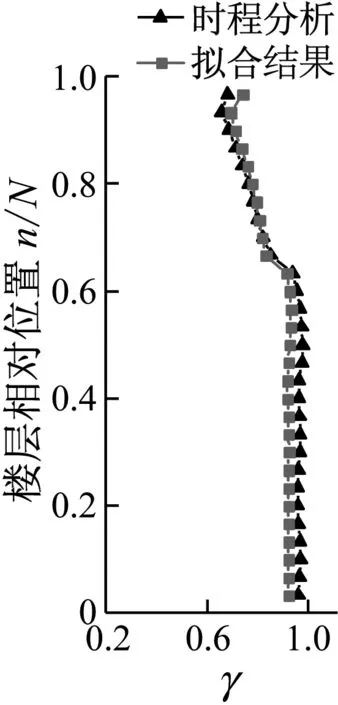
图17 γ时程分析结果与拟合结果对比

5 工程应用实例

为验证所提出层间位移减震域预测式(13)和(14)，以某实际工程为例，进行减震设计分析。该工程地下1层，地上主体建筑28层，地下一层层高4.7 m，地上结构层高为2.8 m，所在地区抗震设防烈度为8 度，设计地震分组为第二组，基本加速度值为0.3g，丙类建筑。图18为该工程的建筑立面图。

原结构Y向第7层至第22层，层间位移角均大于1/1 000，超过《抗规》多遇地震下的层间位移角限值，层间位移角最大超限达到18%，如图19所示，根据原结构层间位移角倒数值即可得该结构的层间位移目标减震比。

图18 建筑立面图

沿结构多层均匀布置黏弹性阻尼器，布置方案及阻尼器布置层位置参数λ如表2所示。其中单个黏弹性阻尼器的阻尼系数取为240 kN·sec/cm，刚度为360 kN/cm。

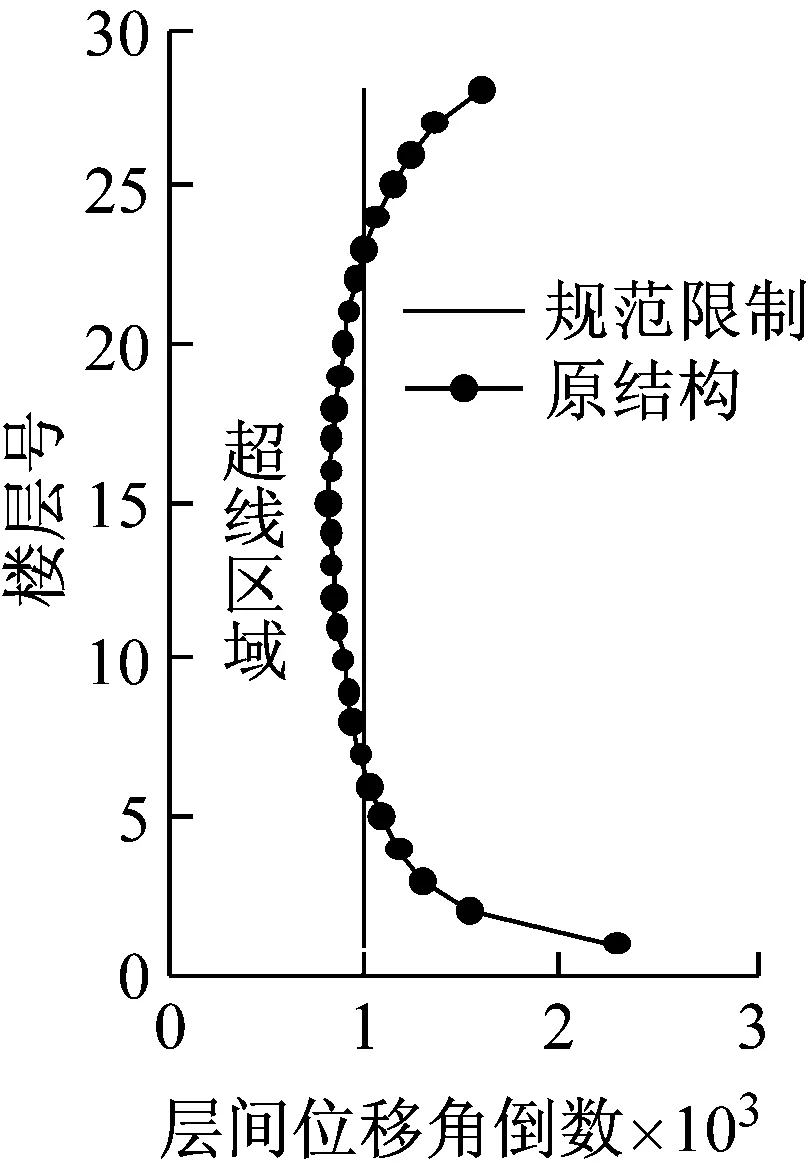
图19 Y向层间位移角倒数

选用2.1节所提7条地震波进行非线性动力时程反应分析，根据预测公式，选择黏弹性阻尼器参数及布置层算出结构层间位移减震比γ，控制γ小于减震目标比值则可以满足《抗规》中层间位移角限值。表3为减震目标与减震效果对比，该布置方案可以满足规范要求，且预测理论值γ与时程分析结果误差均小于10%。

图20～图22为地震作用下结构层间位移减震比、层间位移以及层间位移角倒数预测值与时程分析结果对比，其结果能够较好吻合，从而验证了上文所提出的层间位移减震比γ拟合公式的准确性。

表2 阻尼器布置层位置参数λ

表3 减震目标与减震效果对比

图20 层间位移减震比对比

图21 层间位移对比

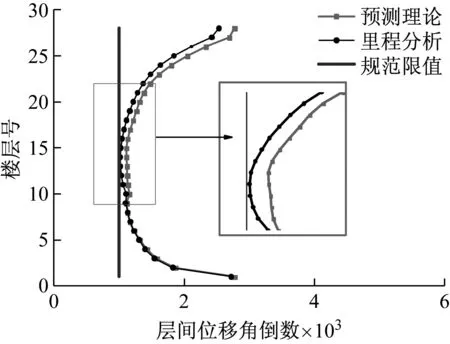
图22 层间位移角倒数对比

6 结 论

对带黏弹性阻尼器结构进行地震作用下的非线性动力时程分析，研究黏弹性阻尼器层间位移减震域，分析了不同楼层结构、阻尼器布置层位置及黏弹性阻尼器参数与层间位移减震比的变化规律，提出黏弹性阻尼器减震结构基于位移减震域的设计方法，结论如下：

(1) 黏弹性阻尼器参数Kd对楼层减震影响主要体现在布置层，结构层数对布置层的层间位移减震比基本无影响。黏弹性阻尼器参数Cd不仅会不同程度影响到相邻层，且随着阻尼器个数的增加，减震域越大。Cd对阻尼器布置层以上的减震效果比布置层以下的效果明显。

(2) 黏弹性阻尼器参数对γKd减震域和γCd减震域可线性叠加，并且不同阻尼器布置层的减震域也可进行线性叠加。

(3) 基于位移减震域的设计方法，对实际工程进行减震分析，根据预测公式，选择黏弹性阻尼器参数及布置层算出结构层间位移减震比γ，对比预测理论值与时程分析结果，误差范围介于0.24%～9.27%，能够较好吻合。

文中提出的以层间位移比和位移减震域的减震结构地震响应分析方法，适用于使用黏弹性阻尼器减震结构的快速初步设计及设计复核，基于其他类型的阻尼器减震结构今后进一步进行研究。