三维金刚石晶格声子晶体超宽频带隙特性研究

江卫锋， 殷 鸣， 向召伟， 谢罗峰， 殷国富

(四川大学 制造科学与工程学院，成都 610065)

类比于光子晶体[1-2]对电磁波的控制，研究者发现弹性介质周期性排布而成的结构可显著影响弹性波的传播，声子晶体的概念[3]由此被提出。声子晶体对弹性波的调控中尤为重要的一点体现在其具有弹性波带隙。处于带隙频率范围内的弹性波在声子晶体中沿任意方向传播都会受到抑制[4]。因此，以声子晶体为依托开发出的新型功能材料和结构器件等将具有非常广阔的应用空间。将其用于隔音降噪，可在音源或是噪声传播路径中设置声子晶体屏障，从而隔离噪声[5-6]；用于减振，能为高精密的机械系统[7-11]或者是大型的土木工程提供无振动工作环境[12]。

数十年来研究人员对声子晶体的带隙(特性做了广泛研究。Yu等[13]提出一种散射体通过颈状结构与基体连接的二维声子晶体结构模型，获得了低频带隙，相关几何参数可调控其带隙特性。Wang等[14-15]研究了一类含共振单元的声子晶体，讨论了结构几何参数对带隙特性的影响，并根据带隙边界的振动模态发展了近似等效模型预测带隙的边界。刘荣强等[16-17]设计了一类板状声子晶体结构，并研究了其振动带隙特性，为声子晶体在隔振领域的实用化提供了新的设计思路。近年来，研究者也逐渐把研究的目光投向能够在空间三个维度上都获得宽频带隙的三维声子晶体结构。Chen等[18]设计了一类双连续的三维声子晶体结构，在简单立方晶格、体心立方晶格和面心立方晶格三种周期形式下分别获得了29%、54%和55%的最大相对带隙宽度。Matlack等[19]提出一种将钢块嵌与聚合物基体的简立方三维声子晶体结构，该结构的相对带隙宽度可达62%。Jiang[20-21]等研究了木堆结构的声子晶体，结果显示得到的相对带隙宽度小于30%。Delpero等[22]设计了一种由中空桁架构成的三维结构，相对带隙宽度达54.5%。另外，一些周期性结构在具有弹性波带隙的同时还能获得光子带隙，这类周期性结构被称为声光子晶体[23-26]。声光子晶体由于其在设计声光器件方面的巨大潜在价值正备受关注。

总体而言，目前对三维声子晶体的研究相对较少，且其中大部分结构获得的带隙宽度不够宽，而带隙的宽度很大程度上又影响着声子晶体的适用范围和稳定性。对此，本文设计了一种按金刚石晶格排布的三维“球-柱”结构。利用有限元方法计算了其能带结构，获得了超宽频的弹性波带隙；计算了带隙边界的振动模态，以研究宽频带隙的形成机理；分析了几何参数对带隙宽度的影响，以实现对弹性波传播的人工调控；计算了有限周期个数下该结构的弹性波透射谱，研究弹性波在结构中的传输特性。利用平面波展开法计算了该结构的光子能带结构，考察其是否具有光子带隙。

1 结构模型及计算方法

如图1(a)所示为结构的扩展单胞图，直径为D的介质球处于金刚石晶格的格点位置，晶格常数为a，相邻介质球之间通过直径为d的介质柱相连接，最终得到由单一材料形成的连续自支撑结构。图1(b)为结构的原胞，它由在扩展单胞中处于同一体对角线上的两个立方体顶点分别连接其邻近的三个面心所形成的平行六面体截取得到。图1(c)为金刚石晶格的布里渊区和不可约布里渊区示意图。

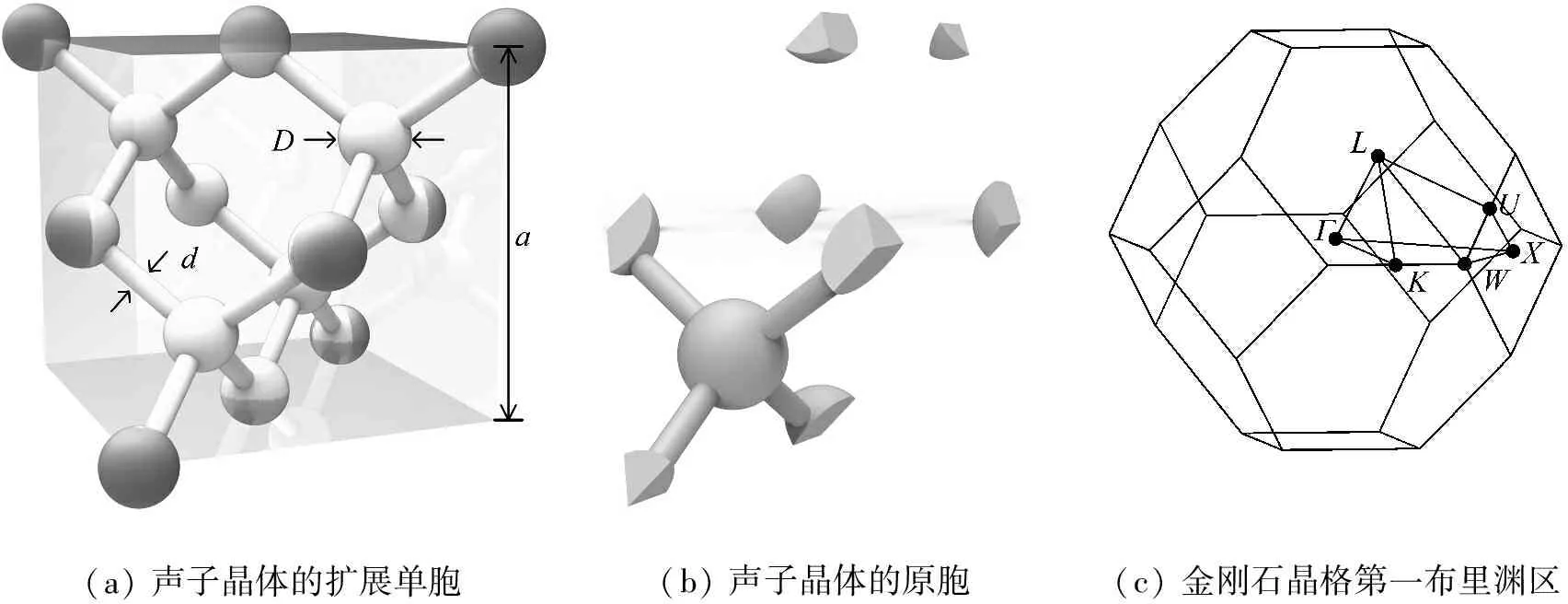
(a) 声子晶体的扩展单胞(b) 声子晶体的原胞(c) 金刚石晶格第一布里渊区

图1 声子晶体结构及金刚石晶格的第一布里渊区

Fig.1 The phonon crystal structure and the first Brillouin zone of the diamond lattice

目前对声子晶体能带结构的计算较多采用有限元法，利用商业有限元软件中的固体力学模块可数值计算声子晶体的能带结构，该模块下弹性波在介质中传播的控制方程为

(i=1,2,3)

(1)

式中：ρ为密度；ui为位移；t为时间；cijkl为弹性常数；xj(j=1,2,3)分别表示坐标变量x，y和z。

根据周期结构中波传播的Bloch定理，位移场u(r)可表示为

u(r)=ei(k·r)uk(r)

(2)

式中：r=(x,y,z)为位置矢量，k=(kx,ky,kz)为第一布里渊区内波矢，uk(r)是与声子晶体具有相同周期性的矢量函数。

离散化后原胞本征值方程为

(K-ω2M)U=0

(3)

式中:K为刚度矩阵；M为质量矩阵；U为节点位移。

将式(2)描述的Bloch定理沿周期性方向应用在原胞模型的边界上，边界位移满足

U(r+a)=ei(K·a)U(r)

(4)

式中：r为边界上节点的位置矢量；a为声子晶体格矢基矢量。

结合式(4)边界条件，令波矢k沿着不可约布里渊区的边界取值，求解本征值方程式(3)，最终可得到声子晶体能带结构。

2 结构模型及计算方法

2.1 弹性波带隙特性

本文计算中所用到的结构材料参数为：密度ρ=2 330 kg/m3，横波速度ct=5 360 m/s，纵波速度cl=8 950 m/s。带隙宽度通常采用归一化后无量纲的相对带隙宽度表示，定义为2(fup-flow)/(fup+flow)，其中fup和flow分别为带隙上、下边界处的实际频率值。取D=0.35a，d=0.06a，计算得到能带结构如图2(a)所示，图中纵坐标采用归一化频率，定义为Ω=fa/ct。可以看到在图中第十二和第十三条能带之间出现一段超宽频的完全带隙，带隙范围为0.434 5<Ω<1.895，其相对带隙宽度达到了125.4%。相比较而言，该金刚石结构声子晶体的带隙宽度已明显大于绝大多数目前其他已有三维声子晶体结构的带隙宽度。为进一步研究该宽频带隙的产生机理，计算了带隙边界位置结构的振动模态。图2(b)为带隙上边界的振动模态，表现为位于同一体对角平面内的连接柱在面内大幅弯曲振动，并带动介质球小幅地摆动；图2(c)为带隙下边界的振动模态，处于体对角线上的介质球和位于面心及顶点位置的介质球作反向振动，连接柱则类似于弹簧作受迫振动。可见介质球和连接柱在一定方向上的共振是宽频带隙产生的最主要原因。另外，在能带结构中带隙是以较低能带的极大值点和较高能带的极小值点为边界的，且能带极值在不可约布里渊区边界的高对称点取得。而金刚石晶格的布里渊区为截角八面体，非常接近于球形，各高对称点处对应波矢幅值大小较为接近，因此对应的频率大小也比较接近，这使得同一能带上频率极大值和极小值间相差不会很大，从而有利于在两条能带之间形成更宽的带隙。其次，该金刚石 “球-柱”结构与简单立方 “球-柱”结构相比，由于面心和体对角线位置上介质球的引入，使得结构对称性降低，这有利于能带简并的解除从而拓宽带隙。

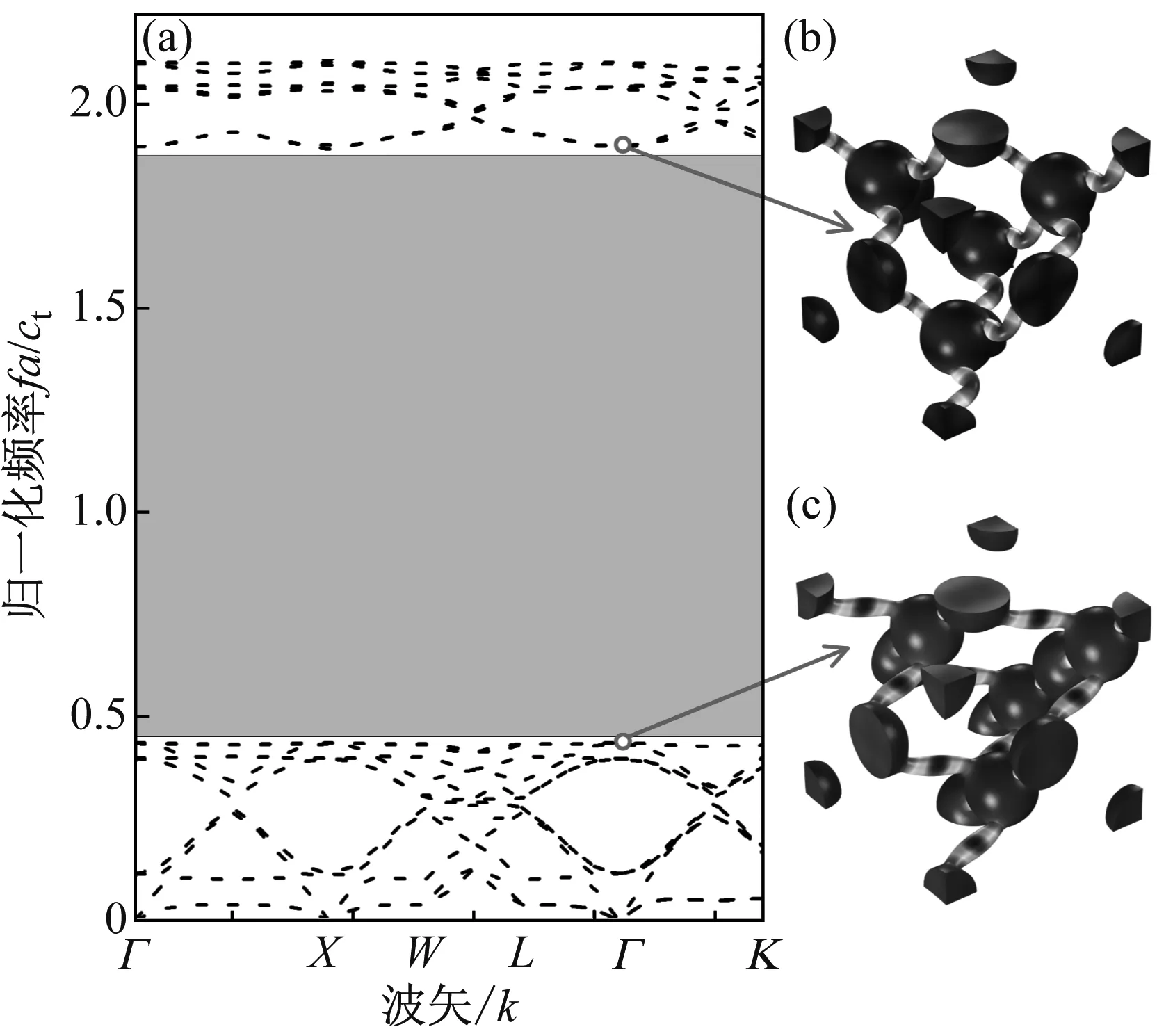
图2 声子晶体的能带结构带隙边界振动模态

2.2 几何参数对带隙宽度的影响

带隙的调控密切关系着声子晶体在减振降噪等方面的实际应用。考虑通过改变结构的几何参数来调整结构从而实现对带隙的调控。图3(a)为d/a=0.06时带隙上、下边界频率以及相对带隙宽度随介质球直径变化的情况。图中显示随着介质球直径增大，带隙上界频率显著变化，其频率值一开始迅速增大然后逐渐减小，带隙下界频率则是先缓慢减小而后逐渐增大。相对带隙宽度由此呈现出先增大后减小的变化趋势，在D/a=0.34附近达到最大。图3(b)为D/a=0.34时带隙上、下边界频率以及相对带隙宽度随连接柱直径变化的情况。随着连接柱直径增大，带隙下边界的频率变化更为明显，其频率值近乎线性地增大，而带隙上界频率缓慢减小。结构的相对带隙宽度随连接柱直径增大而不断减小。在几何参数D/a=0.33，d/a=0.05时，该结构的相对带隙宽度可以达到144.5%，基本是目前已被研究的结构中能够得到的最大相对带隙宽度。当然实际应用中介质球和连接柱的直径大小的取值还需要结合结构的强度和稳定性考虑。以上分析表明介质球直径D主要影响带隙上边界频率而连接柱直径d主要影响带隙下边界频率，D和d的改变显著影响带隙宽度，它们是实现带隙调控的一组关键参数。

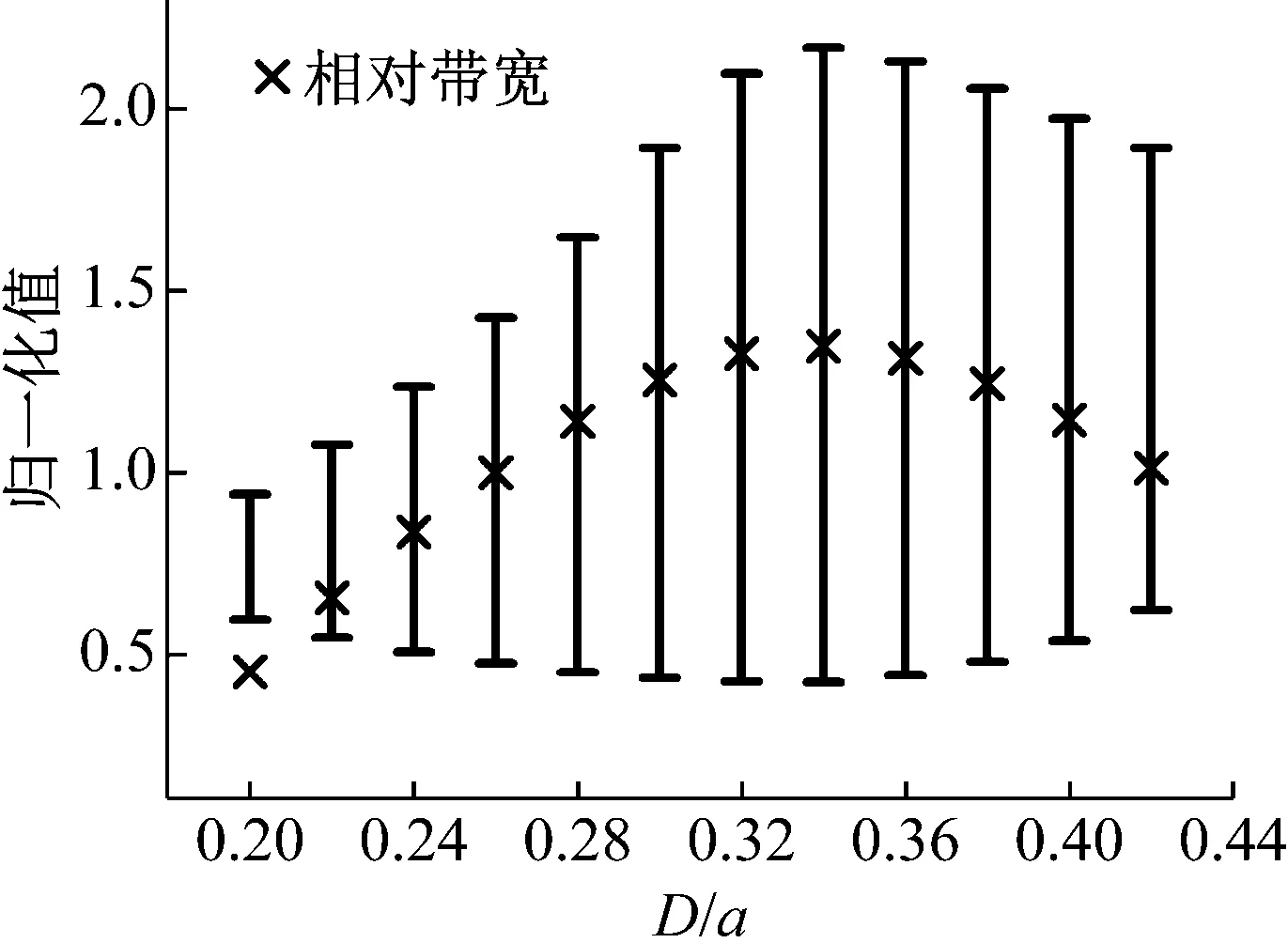
(a)

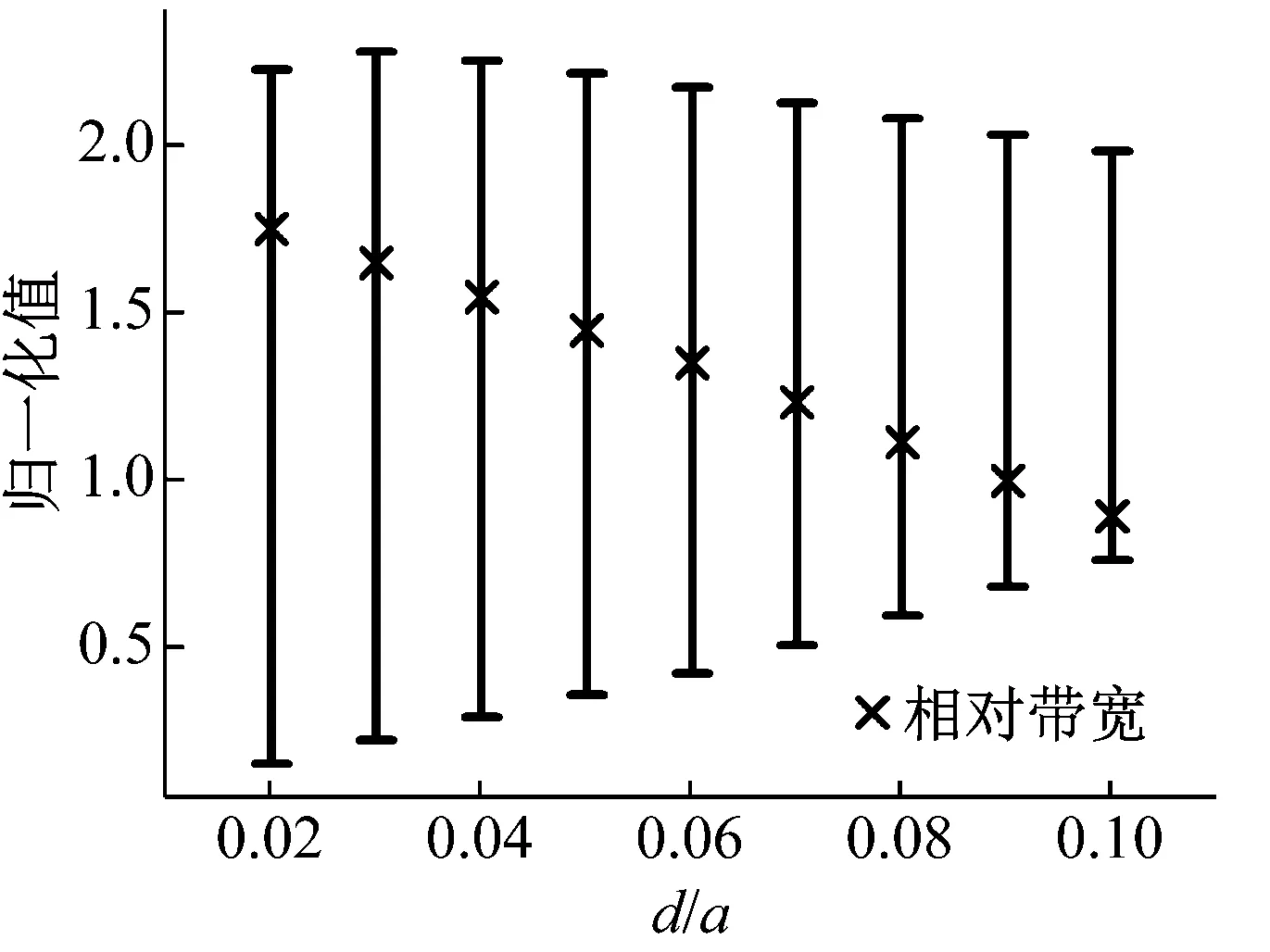
(b)

2.3 弹性波传输特性

选择有限层数的扩展单胞排成一列，在其四个侧面施加周期性边界条件，通过在模型左端边界施加激励，测量模型右端边界的输出响应可计算得到透射谱。图4(a)中实线为D/a=0.3，d/a=0.06时，由七层扩展单胞组成的有限周期结构的透射谱。可以看到频率域内出现非常大的振动衰减区域，其归一化频率范围为0.478 6<Ω<1.954，与图2能带结构中的带隙位置基本吻合。在带隙的中间位置振动衰减达到最大，图4(b)为带隙中Ω=1.213时完整结构的位移场分布，该频率下振动向右传递一个周期后无法沿着声子晶体结构继续传播。通过移除扩展单胞中两个体对角线上格点处的介质球，由连接柱直接在格点处连接，可构造出存在缺陷的结构。该缺陷结构的透射谱如图4(a)中虚线所示，能够看到在原带隙频率范围内出现频率范围非常小的五段通带。图4(c)为通带内Ω=0.753 7时结构的位移场分布，此时振动局域在缺陷处并沿着缺陷传播。值得注意的是，与常见二维声子晶体移除散射体引入线缺陷后在原带隙内几乎形成一条完整连续通带相比，引入缺陷后的金刚石结构声子晶体得到的是多段频率范围非常小且分隔开的通带。另外，通带之间仍然存在着带隙，只是带隙中的振动衰减程度大幅度降低。这是由于宽频带隙的产生主要是由介质球和连接柱的共振引起，结构周期性对带隙的影响作用相对更弱一些。此外，“球-柱”这种结构形式的连续性使得结构中形成的缺陷也并不完全。因此，该结构对处于带隙频率范围内的弹性波传播的抑制作用非常强且比较稳定。

(a) 有限结构的透射谱

(b) Ω=1.213时结构的 (c) Ω=0.753 7时结构的

2.4 结构的光子带隙

同时具有弹性波带隙和光子带隙的声光子晶体结构可以用于设计开发基于声光交互条件下的应用器件如声光传感器、声光开关、声光波导[27-28]等。通常具有全方位声光带隙的一维和二维声光子晶体结构较为常见，而由于分别有利于声子结构和光子结构的拓扑参数不同，三维声光子晶体结构则难以构建。Maldovan等推测固体材料和空气分别形成连续独立网络的三维结构可能同时产生弹性波带隙和光子带隙。因此，本文利用平面波展开法计算了该金刚石晶格“球-柱”结构的光子能带结构。取材料折射率n=3.6，几何参数D/a=0.33，d/a=0.1，计算得到能带结构如图5所示。可以看到在归一化频率0.553 1<Ω<0.635 6的范围内得到一段光子带隙，相对带隙宽度为13.9%。对于三维光子晶体，金刚石类结构相较于其他类型结构通常能得到更宽的带隙，相对带隙宽度一般在10%～30%[29]。因此，可以认为该金刚石“球-柱”结构得到的光子带隙宽度处于一个较宽的范畴。

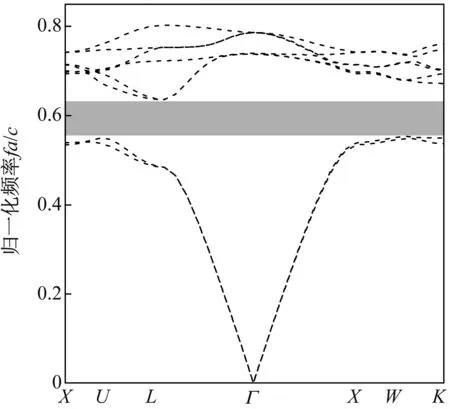
图5 能带结构

3 结 论

本文设计了一种由位于金刚石晶格格点处的介质球通过介质柱连接形成的三维声子晶体结构。该连续的结构由单一材料组成，具有良好的自支撑性。因此该结构形式有利于直接通过增材制造技术制备，而对于一些不宜直接成型的材料，可采用先制造出消失模具然后注塑的间接成型方式。利用有限元方法计算了其能带结构、振动模态和透射谱。结果表明，该三维金刚石晶格声子晶体结构可获得超宽频段的弹性波带隙。宽频弹性波带隙的产生主要由周期性排布的介质球和连接柱在一定方向上的共振引起。此外，金刚石晶格的布里渊区接近球形，这也非常有利于带隙宽度的拓宽。介质球直径D和连接柱直径d的变化分别主要影响带隙上边界和带隙下边界频率。连接柱直径一定，结构的相对带隙宽度随介质球直径的增大呈现先增大后减小的趋势；而介质球直径固定，带隙宽度随连接柱直径的增大而一直减小。因此，对于该类金刚石晶格“球-柱”结构，通过改变几何参数实现其带隙的调控和优化是较为直接且有效的。在几何参数D/a=0.33，d/a=0.05时，结构的相对带隙宽度可达到144.5%，远大于目前现有其他类型的三维声子晶体结构的带隙宽度。值得注意的是，该几何参数下结构的孔隙率达到84.6%，这使得该结构还呈现出轻量化的特点。该三维金刚石晶格声子晶体结构对处于带隙频率范围内的弹性波传播具有非常强的抑制作用，而且由于该结构是连续的且带隙主要有介质球和连接柱的共振引起，所以即使是在引入缺陷后的结构中仍能产生一定宽度的带隙且带隙内振动衰减超过100 dB。因此可以认为该结构对处于带隙频率范围内的弹性波传播的抑制作用强且稳定。此外，该结构在可打开超宽频的弹性波带隙的同时还具有较宽的光子带隙，其相对带隙宽度可达到13.9%。该三维金刚石晶格声子晶体结构可用于减振降噪材料和新型声光器件的设计开发。