柔性膜结构风致振动中的流固耦合效应研究

孙芳锦， 毕 鹏， 吕艳卓

(1.东南大学 混凝土及预应力混凝土结构教育部重点实验室，南京 210096；2.辽宁工程技术大学 建筑工程学院，辽宁 阜新 123000)

风与膜结构的流固耦合作用是被研究人员广泛关注但尚未深入研究的前沿课题之一。随着计算机软硬件技术的迅速提高，数值模拟方法已发展成为分析风与膜结构流固耦合作用的重要工具。目前研究膜结构风振中的流固耦合效应的数值方法包括弱耦合分区法、强耦合分区法和强耦合整体法[1]。弱耦合分区法是在每一时间步内先对流体控制方程和结构控制方程分别独立求解，然后将作用在流体域模型上的气动力荷载通过流体和结构的交界面传递给结构域模型，用来预测结构的位移，然后再将结构的位移作为新的荷载传递给流体域，此过程如此反复，直到结果收敛于指定值。强耦合分区法就是在流体域和结构域各自求解器的基础上再增加一次迭代循环，在每一个时间步求解非线性方程组，计算出全场变量的值。强耦合整体方法是指在每一时间步内对流体控制方程和结构控制方程同时联立求解；狭义的说，就是对整个流固耦合问题用一个方程组表示并进行求解[2-4]。

国内外学者大都采用强耦合分区法或弱耦合分区法对膜结构风振中流固耦合效应进行了研究[5-9]；采用强耦合整体方法计算流固耦合问题的研究还非常有限[10-12]，但强耦合整体方法在稳定性和精度等方面却显示出其优势。文献[13]推导出了风与膜结构的流固耦合计算的强耦合整体方程，并对典型形状膜结构的风振流固耦合计算进行了分析，研究结果表明采用强耦合整体方法求解风与膜结构的流固耦合作用具有在精度和稳定性方面都具有优势，但由于强耦合整体方法采用一个非线性方程组表示流固耦合系统，通常需要采用Newton方法线性化后进行求解。在求解该方程过程中，大量的机时都耗费在了对雅可比矩阵的反复集成和相应线性体系解的Newton修正中[14-15]，这往往会导致该问题的计算量非常大，因此对强耦合整体方程进行高效的求解是需要重点解决的问题之一。

本文针对柔性膜结构经历大变形的特点，对传统投影法进行修正来求解上述强耦合整体方程，在经典投影法的基础上，在校正步中引入压力修正因子迭代修正使原始动量方法中隐性定义的压力约束条件得到满足，并给出了该方法求解的过程。应用提出的修正投影法对经典二维流固耦合问题和三维柔性膜结构风致流固耦合作用进行计算，评估了本文修正投影法的性能和效率。

1 控制方程和边界条件

1.1 流体控制方程

流体控制方程由为不可压黏性Navie-Stokes方程(简称N-S方程)，即连续方程和动量方程

▽·νf=0

(1)

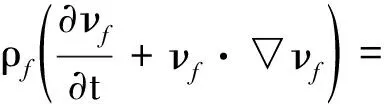
(2)

式中:νf为流体流动速度；▽为空间梯度;ρf为流体密度;σf为流体的全应力张量(压力和黏性力)，σf=μ[▽vf+(▽vf)T]-pI，μ是流体黏度；p为流体压力;fBf为流体体积力。

1.2 结构控制方程

膜结构可以看成是经历大变形的弹性体，其控制方程可由Total Lagrangian方程描述为

▽·σl+fs=0

(3)

上式表示T.L.方法中，差分平衡方程基于初始未变形位形的表达；σl是Piola-Lagrange应力张量，它是相对于未变形表面已发生变形位形的应力。

1.3 流体和结构的耦合

引入线弹性模型来处理流体域的变形，解决流体域和结构域交界面处的数据传递问题，实现流体和结构的耦合。线弹性模型的方程为

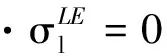
(4)

(5)

(6)

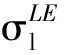
(7)

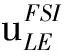
流体和结构在交界面上的耦合条件为

(8)

(9)

(10)

式中:νs是结构速度;us是未知结构位移;σc是Cauchy应力，σc=FσpFT/J，J=det(F)是雅可比行列式;ns=-nf,nf是流体边界面的外法线方向单位向量，ns是流体边界面的外法线方向单位向量。

1.4 流固耦合体系的强耦合整体方程

强耦合整体方程的推导就是对流体域、结构域以及线弹性模型方程进行时间和空间上的离散的过程。流体方程、结构方程和线弹性方程均采用Galerkin有限元法进行离散，时间上的离散采用隐式有限差分方法，具体推导过程可参见文献[13]。

膜结构风致流固耦合问题的加权残差方程fFSI可以写作

2 求解方法

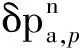
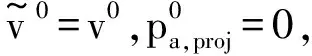
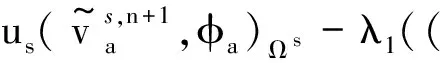
(16)

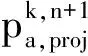
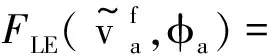
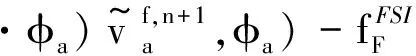
(17)

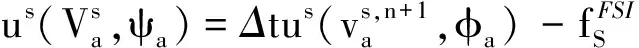
(18)

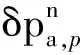
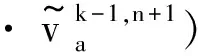
(19)

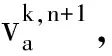
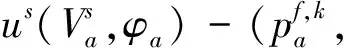
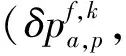
(20)

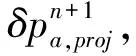
(21)

最后将上述预测得到的速度投影到无散向量场空间，得到非线性方程组的速度、压力和位移

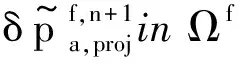
(22)

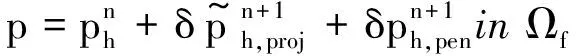
(23)

(24)

3 算例分析

3.1 二维流固耦合问题

这里应用上述模型对典型的流固耦合问题进行了计算[17]。实验中流体水的密度ρf=1 000 kg/m3，固体为类似橡胶材料，几何尺寸如图1所示。试验共分为FSI1、FSI2和FSI3三个试验，其中FSI1试验为稳态试验，FSI2和FSI3试验为非稳态流固耦合二维计算，这里分别对FSI2和FSI3试验进行计算。试验中为低雷诺数情况，试验中计算域长度L=2.5 m，高度H=0.41 m，结构模型包含刚性圆柱和其右后的一弹性杆，圆柱圆心位置(从计算域左下角位置算起)C为(0.2,0.2,)，半径为0.05。弹性结构杆件的长度为l=3.5，高H=0.02；右下角的位置是(0.6,0.19)，且其左侧与固定圆柱是完全连接的。整个结构控制点A(t)的位置是A(0)=(0.6,0.2)。受篇幅所限，这里仅给出模拟FSI3试验的计算结果。

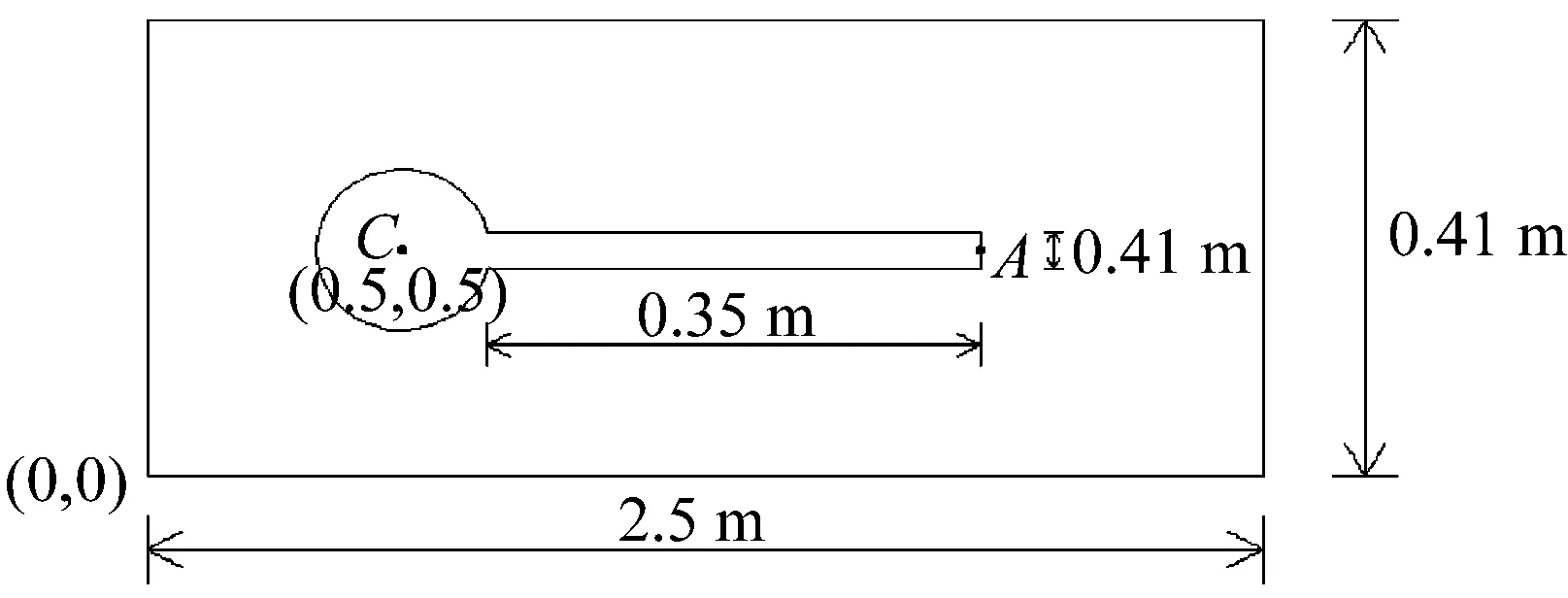
图1 经典流固耦合问题几何尺寸

设定λ1≈104经过多次修正迭代得到的结果与采用Newton-Rapshon求解方法的结果和原试验结果进行了对比。图2和图3分别给出了本文计算的弹性梁端结点A的不同方向位移时程，以及作用在圆柱和梁上的升力和阻力。

从图中可以看出，本文引入修正因子的投影法的计算结果与采用Newton-Rapshon求解方法和原试验结果非常接近，说明本文方法的正确性。

为了说明本文方法的求解效率，表1给出了采用本文方法计算得到弹性梁端结点A的x方向位移dx和y方向位移dy随不同修正迭代的误差范数变化，并与其他方法结果进行了对比。

从表1中可以看出，与传统Newton-Rapshon法相比，经过同样的迭代次数，本文中引入修正因子的投影方法的误差范数要小得多；且本文的方法只需经过较少的迭代次数便可以达到较小的误差，证明了本文方法的收敛速度快，误差小。

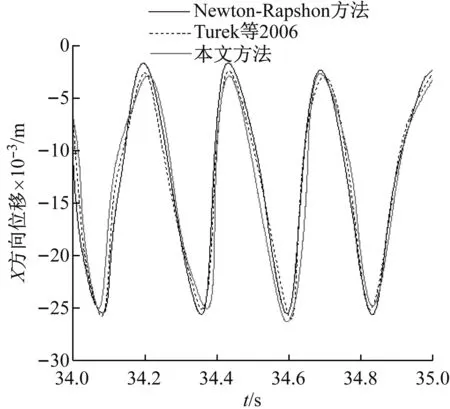
(a)

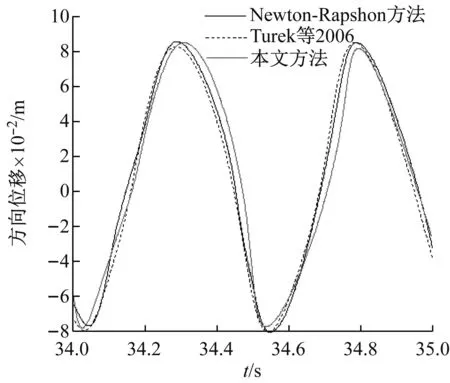
(b)

Fig.2 Displacement time history comparison at different directions of nodeA

表1 弹性梁端结点A的误差范数比较

3.2 三维柔性膜结构风致振动流固耦合效应分析

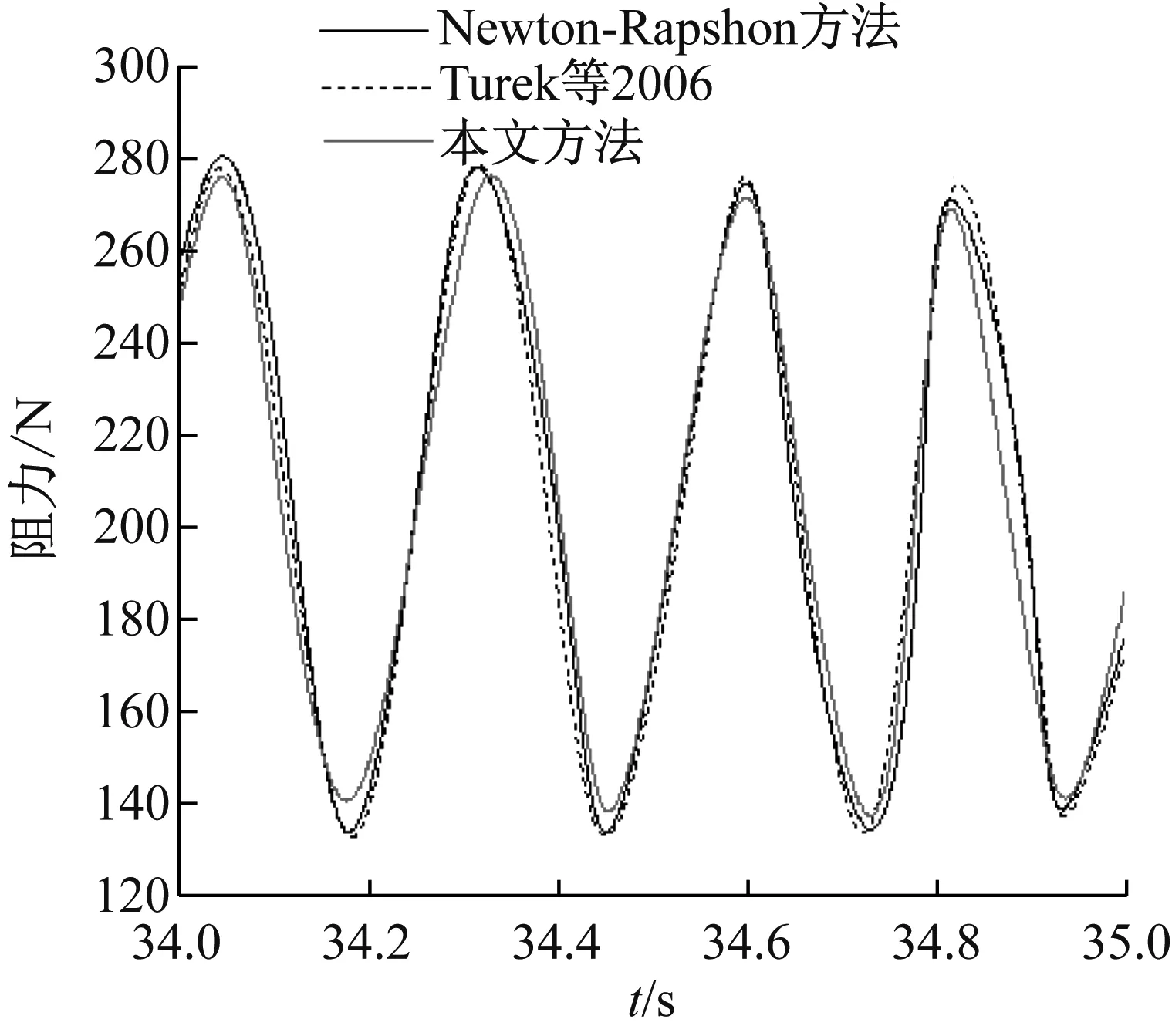
(a)

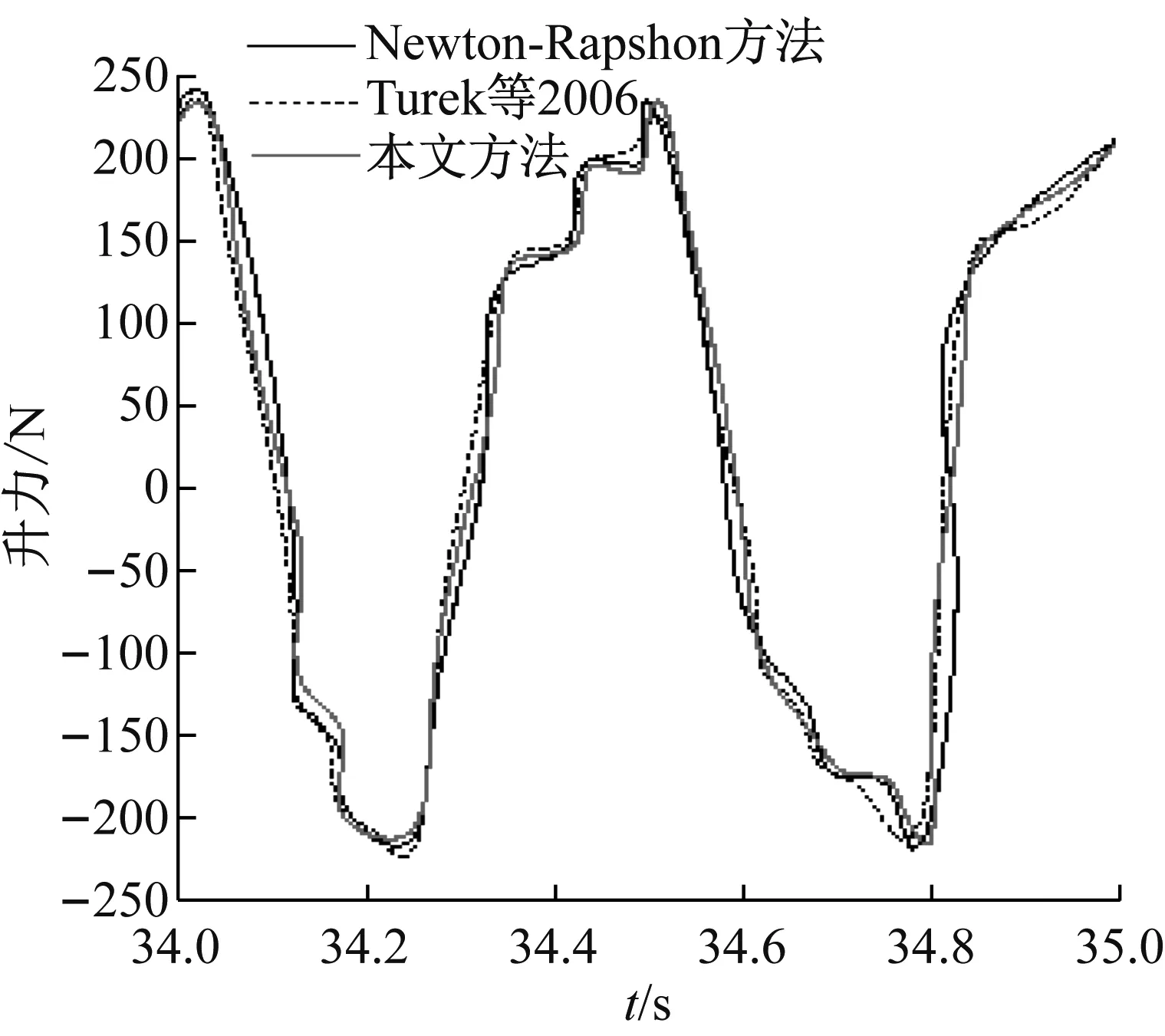
(b)

这里以典型的鞍型膜结构为例，应用以上的强耦合整体方法程序进行风振响应分析计算。膜结构的计算简图如图4所示，其基本参数如下：跨度L=20 m，高度H=5 m，矢跨比f/L=1/8，预张力T=2.0 kN/m，薄膜厚度为1 mm，单位面积的质量g=1.25 kg/m2，张拉刚度为Et=8.0×105N/m,剪切刚度Gt=1.2×104N/m，泊松比υ=0.3。由于本文重点考察修正投影法的性能，因此暂未考虑湍流的影响。以典型的三维鞍型膜结构为例，应用以上的强耦合整体方法和预处理器对其进行风振响应分析计算，计算中的具体参数设置与文献[13]相同，这里不再赘述。

为了说明本文的修正投影法的计算效率和性能，这里首先分析了修正投影法中修正值λ1对膜结构分区风压系数的影响，其中鞍型膜结构的分区情况见图5。

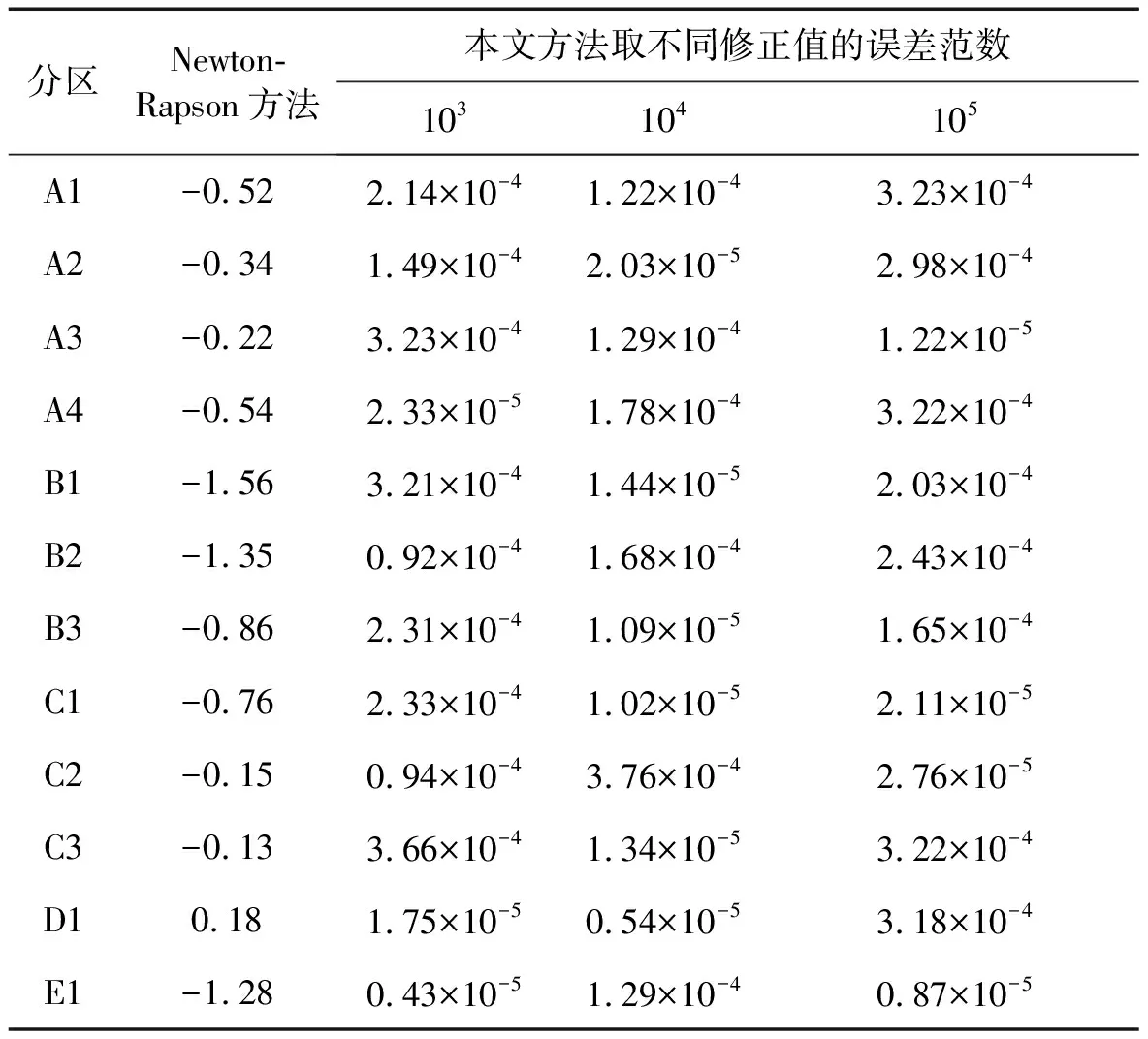
表2给出了本文方法中选取不同修正值时与Newton-Rapson方法的分区风压系数(0°风向角)相比的误差范数，其中Newton-Rapson方法的分区风压系数来自文献[13]，其中迭代次数为10次。

分析表2，可以得出如下结论，

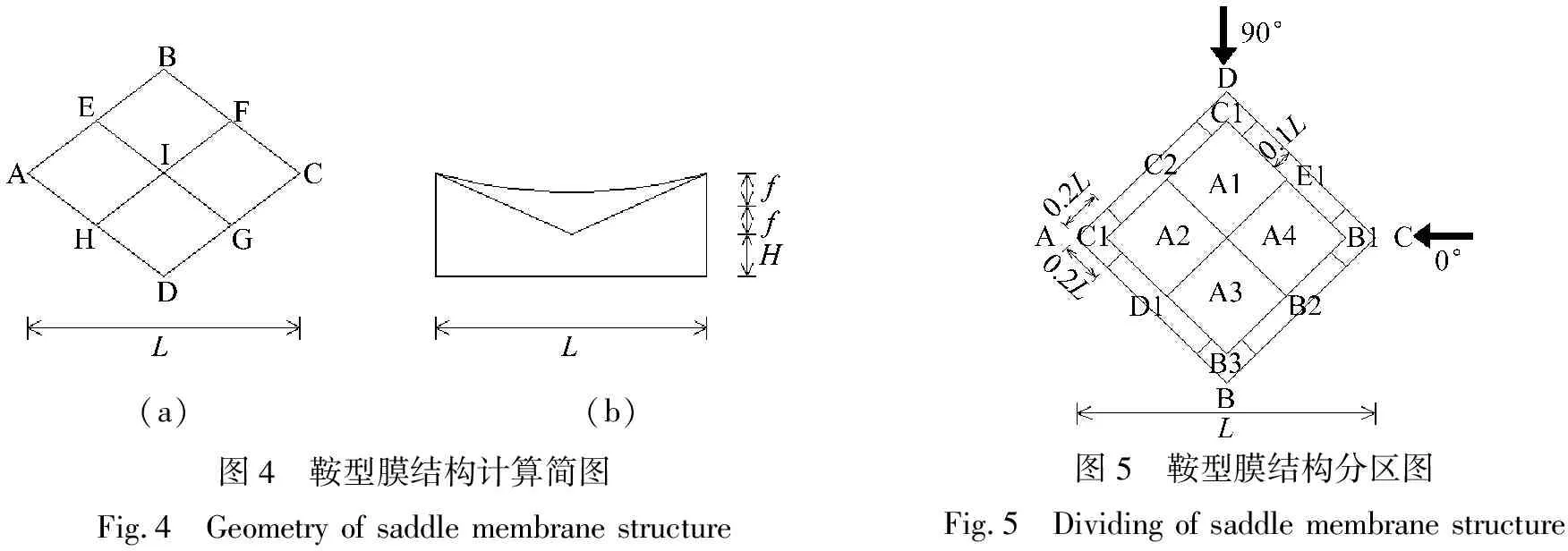
(a)(b)图4 鞍型膜结构计算简图Fig.4 Geometry of saddle membrane structure图5 鞍型膜结构分区图Fig.5 Dividing of saddle membrane structure

表2不同修正值对平均风压系数(均值)的影响

Tab.2Effectsofdifferentmodifedvaluesonmeanwindpressurecoefficients

分区Newton-Rapson方法本文方法取不同修正值的误差范数103104105A1-0.522.14×10-41.22×10-43.23×10-4A2-0.341.49×10-42.03×10-52.98×10-4A3-0.223.23×10-41.29×10-41.22×10-5A4-0.542.33×10-51.78×10-43.22×10-4B1-1.563.21×10-41.44×10-52.03×10-4B2-1.350.92×10-41.68×10-42.43×10-4B3-0.862.31×10-41.09×10-51.65×10-4C1-0.762.33×10-41.02×10-52.11×10-5C2-0.150.94×10-43.76×10-42.76×10-5C3-0.133.66×10-41.34×10-53.22×10-4D10.181.75×10-50.54×10-53.18×10-4E1-1.280.43×10-51.29×10-40.87×10-5

(1) 本文的修正投影法得到的分区风压系数与Newton-Rapson方法计算得到的分区风压系数非常接近，证明了本文方法计算三维膜结构风致流固耦合计算的正确性。

(2) 本文修正投影法的修正值λ1的取值对风压系数的影响并不是很大，可以看到，随着修正值λ1增大，风压系数误差范数的变化并不明显，但是计算中发现，修正值的增大会导致计算机时明显增加，且增加了计算不稳定的风险。因此修正值建议取在一定合适的范围内即可。

表3给出了迭代次数的变化对于风压系数的影响，这里还计算了0°风向角时分区风压系数与Newton-Rapson方法相比的误差范数变化，其中修正值λ1≈103。

分析表3可以看出，修正投影法的计算精度较高，且迭代次数对于风压系数是有重要影响的：迭代次数越大，风压系数的误差范数越小，结果越准确。但是要注意计算结果精确度和计算耗时之间的平衡。计算中发现，迭代次数平均增大达到约20%，计算精度提高约19%，计算耗时平均约增加7%，说明采用修正投影法计算膜结构的风致流固耦合风压系数，计算精度的提高速度是高于迭代次数和计算耗时的，因此如果需要得到更高精度的结果，在计算硬件条件容许的情况下是可以通过增加迭代次数实现的。

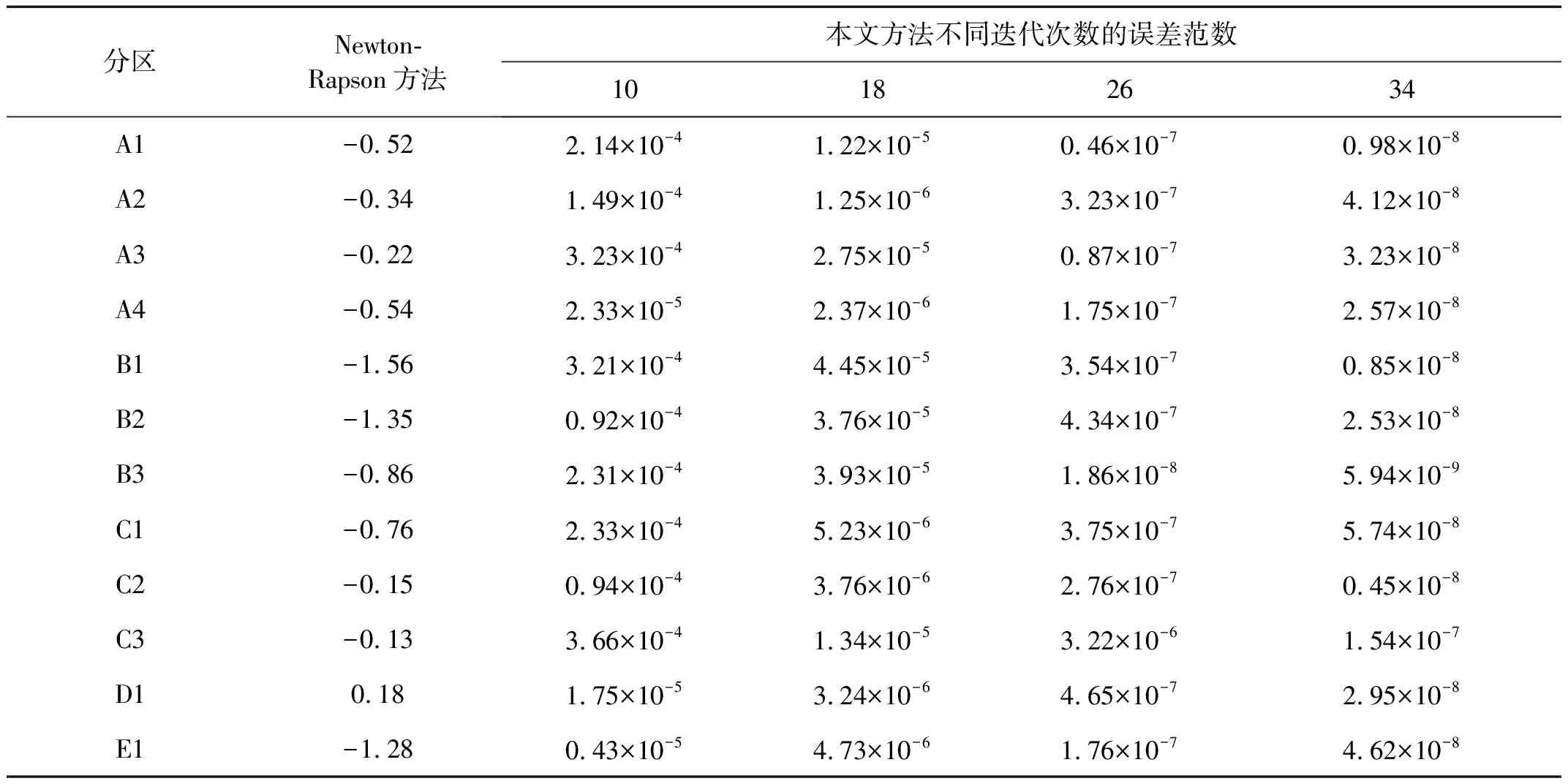
表3 不同迭代次数对平均风压系数(均值)的影响

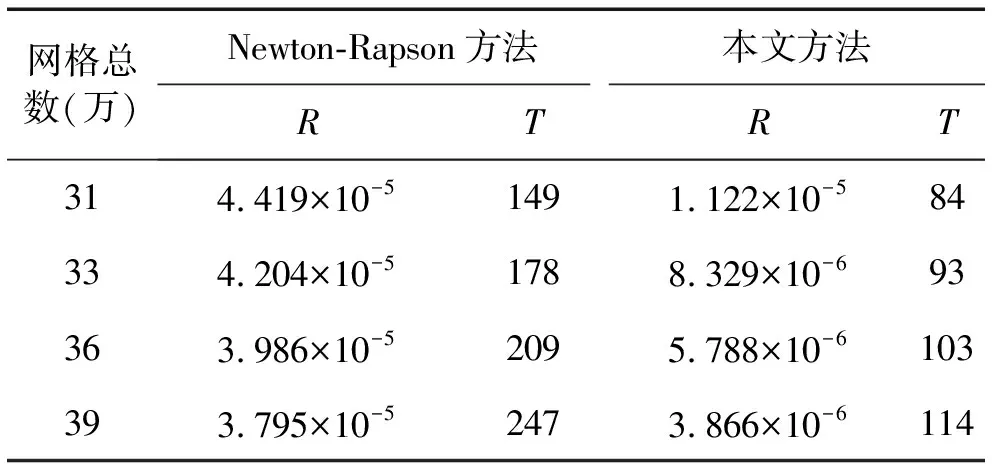
同时，为进一步说明本文修正投影法的计算精度和效率，本文还对比了不同求解方法在不同网格数下计算膜结构中点的前40 s的风振响应时，采用相同迭代数时的相对残差R和耗费机时T(小时)，其中修正投影法的修正值λ1≈103，对比结果如表4所示。

表4不同网格数下的相对残差和耗费机时

Tab.4Relativeresidualsandcomputingtimefordifferentmeshnumbers

网格总数(万)Newton-Rapson方法本文方法RTRT314.419×10-51491.122×10-584334.204×10-51788.329×10-693363.986×10-52095.788×10-6103393.795×10-52473.866×10-6114

分析表4可以看出，

(1) 在同样网格精度和迭代次数条件下，无论采用传统Newton-Rapson方法还是本文方法，随着网格的精细化程度提高，计算相对残差都逐渐减小，耗费机时也都增加。但本文修正投影法的相对残差和耗费机时均小于传统Newton-Rapson方法，说明本文方法的计算精度和效率都是较高的。

(2) 采用传统Newton-Rapson方法时，当网格精度平均提高约10%时，计算精度平均提高约5%，而耗费机时却平均增加了约20%，稳定性基本不受影响，表明网格划分的精细程度对于计算结果的精度和稳定性影响是不大的。

(3) 当采用本文修正投影法时，当网格精度平均提高约10%时，计算精度平均提高约30%，而耗费机时却平均只增加了约10%，稳定性同样基本不受影响；说明在同样网格精度提高的条件下，本文修正投影法的计算精度和效率显著提高，也说明本文方法的计算结果对网格的依赖度较高。

4 结 论

本文针对柔性膜结构经历大变形的特点，对传统投影法进行修正来求解上述强耦合整体方程，应用于二维流固耦合问题和三维柔性膜结构风致流固耦合作用进行计算，得到的主要结论有：

(1) 修正投影法可以用于柔性膜结构的风致流固耦合计算，且其计算精度和效率要高于传统Newton-Rapson方法。

(2) 修正投影法的修正值对于结果的影响不大，而计算迭代次数是影响结果的重要因素.

(3) 采用修正投影法的计算结果对网格的依赖度较高，计算中可以通过增加迭代次数的方法较大幅度的提高计算精度，且计算机时增加相对较少，计算稳定性不受影响。