风轮振动行为与尾迹的关联性研究

李佩林， 马剑龙,2， 汪建文,2， 张彦奇， 姜 勇， 吕文春,3

(1．内蒙古工业大学 能源与动力工程学院，呼和浩特 010051；2．风能太阳能利用技术教育部重点实验室(内蒙古工业大学)，呼和浩特 010051；内蒙古机电职业技术学院冶金与材料系，呼和浩特 010070)

叶片的振动行为会对周围的流场造成一定程度的拉伸和压缩，由于流固耦合效应，叶片的振动行为将更加复杂，故仅从叶片振动行为入手，研究提高风力机气动特性及使用寿命，势必会忽略造成叶片疲劳损伤的一些本质因素，因此研究风力机结构场与流场之间的内在关联机理，是解决风力机结构安全性和运行稳定性的关键所在[1-3]。特别随着风力机大型化和复合材料化发展的趋势加剧，许多结构材料优异的叶片更是因为忽略风轮振动与尾迹发展间的关联属性而惨遭夭折。作为典型的流固耦合问题，在数值计算方面，有效的解耦计算方法仍处于研究阶段，而试验方面，受限于试验设备及落后的监测方法，研究进展缓慢。

国外研究起步较早，典型的Kim等[4]利用CFD揭示了风速及风轮转速对风力机尾迹区及叶尖涡的影响效果，并结合PIV试验证明了风力机轮毂及叶尖附近的流场变化对风力机的动态响应影响最为显著。Maldonado等[5]使用合成射流致动器以提高风力机叶片运行稳定性，发现该装置使叶片的振动显著减小。Bekhti等[6]对比了某两种翼型在运行条件下的流固耦合效应，发现翼型迎角增加，叶片振幅增大。Howland等[7]对偏航条件下尾流结构进行了实验研究，发现风力机适当的偏航可以降风力机的尾流损失。Campbell等[8]利用自主开发的结构求解器结合流体求解器对大型风力机在稳态与非稳态入流条件下的流固耦合进行数值模拟。Viré等[9]使用非线性模型模拟流体与固体之间的相互作用，提出分别单独构建流体和固体动力学方程有限元模型的方法，进行流固耦合求解。Dose等[10]利用几何精确光束理论重建结构变形求解器，使其可以满足大型柔性叶片的流固耦合求解。Sessarego等[11]基于水平轴风力机空气动力学的三维黏性非黏性求解器(称为MIRAS)与用于航空领域的弹性代码FLEX5中的结构动力学模型开发了一中新的流固耦合求解模型。适用于解决叶尖大变形及高风速运行下的风力机流固耦合问题。Hsu[12]开发了新的流固耦合计算方法，利用多物理建模程序构建了风力机三维模型，对不同几何形状的叶片进行了流固耦合分析，该方法适用于湍流条件下风力机气弹响应分析。Hamdoon[13]通过MATLAB编写耦合气动模型和结构模型，使用Newmark隐式时间积分方法，实现数据在结构和流体之间的交换，得到叶片的气动弹性响应。Järpner等[14]基于流固耦合模型对碳纤维材质的风力机叶片进行了数值模拟，得出叶片气动弹性响应特征。

国内研究起步较晚，具有代表性的有Liu等[15]就大型风力机叶片在运行时发生强烈振动展开研究，发现轴向窜动对风力机气动特性的影响最为显著。姚世刚等[16]对风轮进行了全三维流固耦合数值模拟。陈文朴等[17]基于流固耦合研究了在流场作用下叶片结构的稳定性。Lee等[18]对玻璃钢材质的叶片进行流固耦合分析，发现在来流风25 m/s条件下，流固耦合作用使风力机输出功率减小17%。柯世堂等[19]基于大涡模拟(LES)对风力机气动力性能和尾迹流场进行了数值模拟，得出了塔架绕流特性及其表面的气动分布。

综上文献可知，目前对于风轮振动与尾流关联性的分析研究依然处于初步阶段，且多为数值模拟，相关试验的研究较少，且关联性与关联机理尚不明确。

1 测试实验

1.1 测试对象及测试系统

测试对象为木质直径1.4 m小型水平轴风力机，额定尖速比5.5。置于直流式风洞开口端，多场同步测试系统如图1所示。

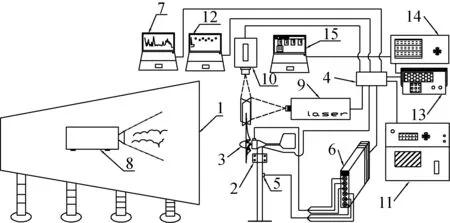
1-风洞；2-偏航装置；3-导流罩；4-同步触发器；5-三向加速度传感器；6-加速度信号采集前端；7-振动加速度采集控制电脑；8-烟雾发生器；9-激光器；10-高频CCD相机；11-激光器电源；12-流场信息采集控制电脑；13-电子负载；14-功率分析仪；15-电信号采集控制电脑

图1 多场同步测试系统

Fig.1 Multi-field synchronous test system

测试系统可实现发电机、塔架、基座振动加速度值与风轮尾迹发展的同步监测，步骤原理如下：

(1)试验工况中风速大小的调节通过风洞的变频器改变轴流式风机转速实现,而风轮转速的调节则通过调节外接电子负载的电阻值实现。

(2)试验开始前，需要利用标定靶盘对拍摄的流场区域进行标定，确定拍摄范围与分辨率，并完成CCD相机对焦等工作，标定完成后不可再挪动相机。偏航拍摄区域为靠近风洞开口端一侧的风力机叶片(即风轮上游)。靶盘标定参数，如表1。

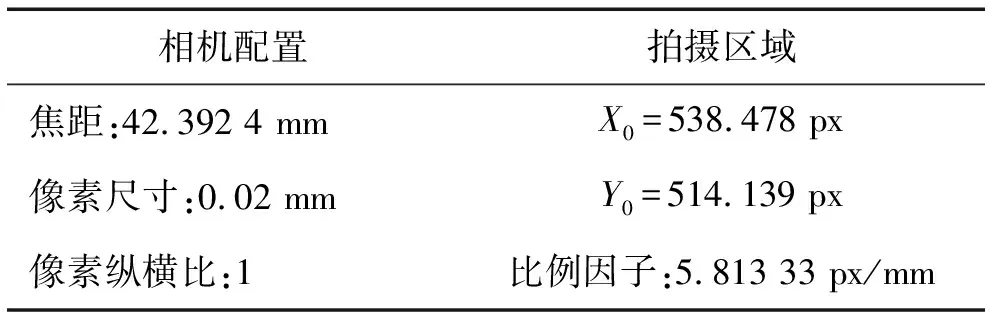
表1 靶盘标定参数表

(3)试验开始后，首先需开启风洞，根据所需风速调节风洞变频器，待出流稳定后，一名测试员触发位于风洞入口段的烟雾发生器，使其发射带有荧光粒子的烟雾并维持数秒。另一位测试员利用同步触发器，同时触发TR-PIV装置及PULSE19装置，开始采集所需试验数据。

(4)振动加速度信号通过与加速度传感器相连的数据线汇总于加速度信号采集前端，并通过网线实时传输回振动加速度采集控制电脑。

(5)风轮尾迹湍流信息则由高频CCD相机拍摄为连续的照片，采样频率1 000 Hz，拍摄时长0.5 s，拍摄数量500张，待拍摄并储存完毕后，所有图片通过与流场信息采集控制电脑连接的网线实现传输。

1.2 测试装置及安装方法

采用丹麦B&K公司最新研发的PULSE19结构振动分析系统完成振动加速度值的采集，如图2所示。

图2 加速度值测试系统PULSE19

采用德国LaVision公司研发的TR-PIV粒子图像测速技术系统完成风轮尾迹流动信息的采集，如图3所示。

图3 尾迹测试系统TR-PIV

加速度信号由四个振动加速度传感器负责采集，1#传感器的安转位置为发电机前端靠近风轮处的侧面，距地面150 cm与风轮轴心同高，2#传感器位于发电机顶端轴线正上方，距地面154.3 cm，3#传感器位于发电机中部侧上方，距地面153.3 cm，4#传感器位于塔架中上部与1#传感器同侧，距地面120 cm，具体安装位置如图6(c)所示。通过对比各传感器输出信号，发现1#与2#传感器信号输出更为可靠，且已有研究表明靠近风轮处传感器的输出信号更接近风轮真实的振动情况[20-21]。传感器X方向垂直于旋转平面指向风轮，Y方向平行于旋转平面水平向外，Z方向竖直向下。传感器通过卡槽固定在垫片内，垫片通过502胶固接在测点处。

运用TR-PIV拍摄风轮尾迹流动信息，高频CCD相机采用仰视拍摄的方式，将CCD相机镜头垂直向上放置在风轮叶片正下方，激光器位于风力机后1 m处发射垂直于旋转平面的水平片光源。该种拍摄方法，降低了相机架设重心，使相机拍摄时更为稳定，有效的保护相机，而又不降低拍摄要求与精度。

试验在位于内蒙古自治区新能源示范基地所属B1/K2型低速低湍流风洞开口实验段内进行，距风洞出口一定距离的适当位置处安装风力机并用紧固螺栓固定于地面，并为风力机机头处安装偏航装置，偏航装置为两个U型卡盘，根据试验所需偏航角度用紧固螺栓将机头与塔架固定。

风轮转速的调节通过美国Fluke公司研制的高精度六相功率检测分析系统Norma5000(如图4)与美尔诺可编程LED直流电子负载M9812(如图5)完成，根据所需转速计算出对应发电机电频率，并通过调节负载电阻，使发电机达到对应电频率，进而实现所需风轮转速。

图4 Fluke Norma5000Fig.4 Fluke Norma5000图5 电子负载箱Fig.5 Electronic load box

通过改变来流风速，尖速比，偏航角构成此次试验的试验工况，来流风速选取10～12 m/s，尖速比选取4.5～6，偏航角选取0°～30°，测试现场如图6所示。

(a) 风洞与风力机(b) TR-PIV安装位置(c) 加速度传感器(d) 信号采集

图6 测试现场

Fig.6 Test site

2 测试结果分析

2.1 频谱响应关联性分析

风轮叶片发生振动后，叶尖位置属于自由端且厚度偏薄，变形量较叶根及叶中大，对流场的挤压与拉伸较明显，故将叶尖附近的流场作为主要研究对象。

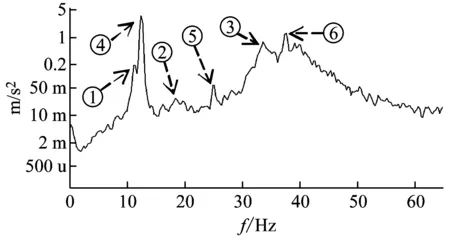
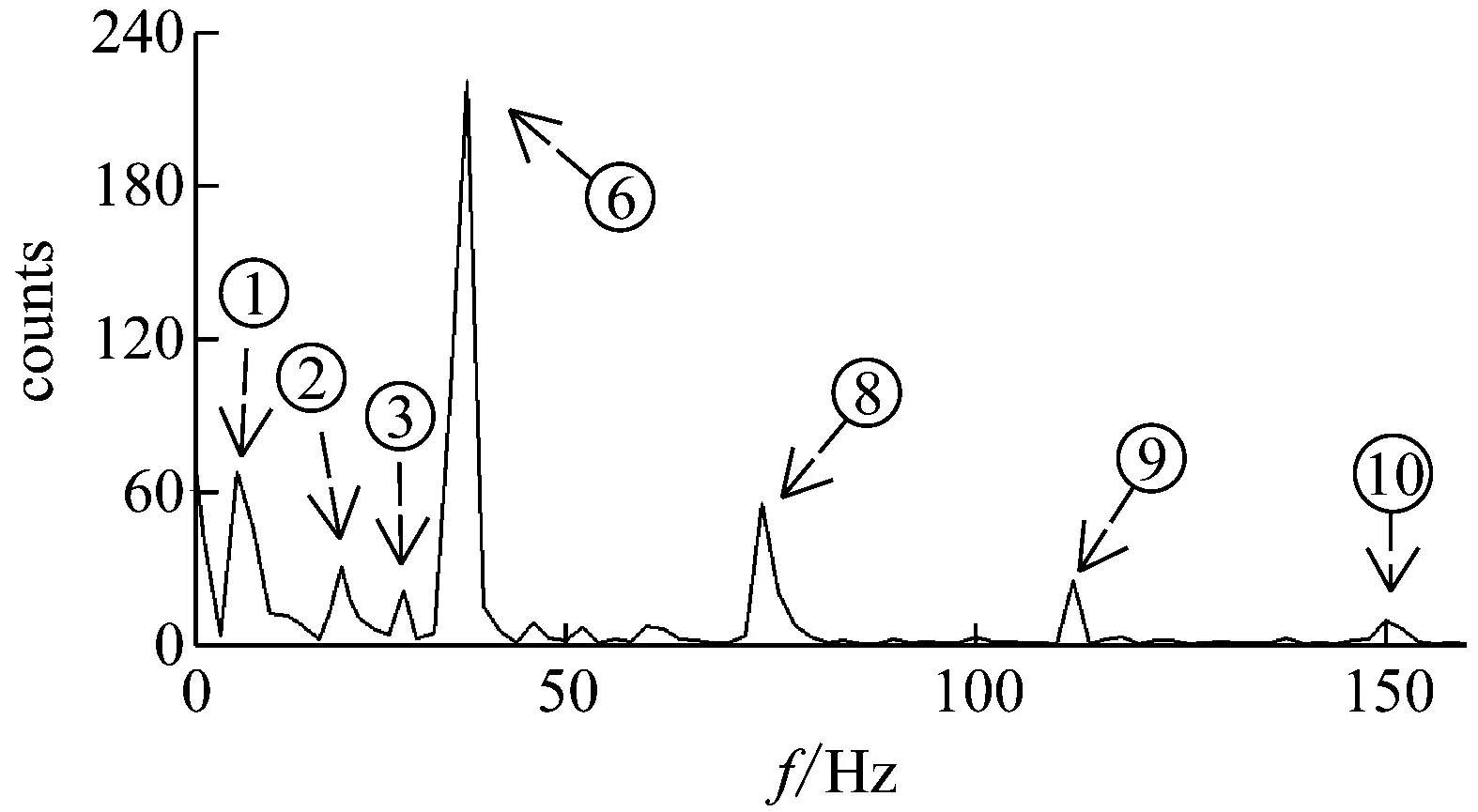
对1#加速度传感器采集的加速度值及靠近叶尖处尾迹流场中的一点进行FFT(快速傅里叶变换)分析，分别得结构场振动谱与流场功率谱，以来流风速v=11 m/s，偏航角β=0°，尖速比λ=4.5，5为例，如图7所示为结构场振动响应谱与流场功率谱。

定义：振动谱加速度值用m/s2表示，功率谱能量值用counts表示。

通过与模态试验参数对比，识别振动谱中各峰值所对应的特征振型，同时计算风轮旋转频率，与其频率相近的就是风轮的基频振动(旋转基频)，因是三叶片风轮，故湍流涡旋的脱落频率为3倍的旋转频率，功率谱中称为一次谐波，如表2所示。

由图7中各分图可发现如下特征：

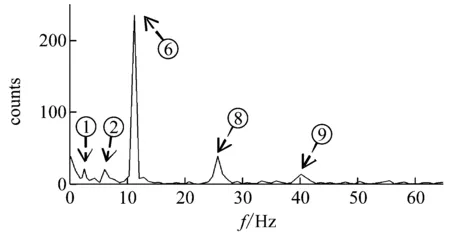
(a) λ=4.5振动谱

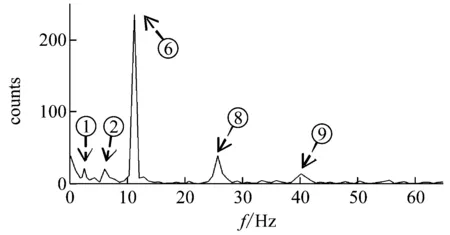
(b) λ=4.5功率谱

(c) λ=5振动谱

(d) λ=5功率谱

(1) 相近频率处振动响应谱与流场功率谱均出现了峰值，证明风轮发生倍频振动、轴向窜动、圆盘效应及1阶振动的能量传递到了流场中。理论分析：流体流动时会产生内摩擦力，流体在运动状态下具有抵抗剪切变形的性质，是流体的固有属性，因此当流固之间发生相互作用时，若不考虑流体密度变化，流体可视为不可压缩流体，具有质量和速度。故将叶尖及其后附近的流体作为一个系统，当来流风速与风轮转速一定时，叶片所受冲量一定，系统水平轴向方向合外力为零。根据动量守恒，当叶片发生位移并与空气发生摩擦和碰撞，叶片振动速度减小，动量减小，而一定质量的空气移动速度加快，动量增加，进而叶尖振动与流体脉动之间形成了一个联动系统，两个不同的物理场之间发生密集的动量传递与交换，当叶片振动频率变快，流体的脉动频率也增大。故当叶片发生特征频率下的振动时，叶尖附近的流体也会随着叶片发生相似的脉动。

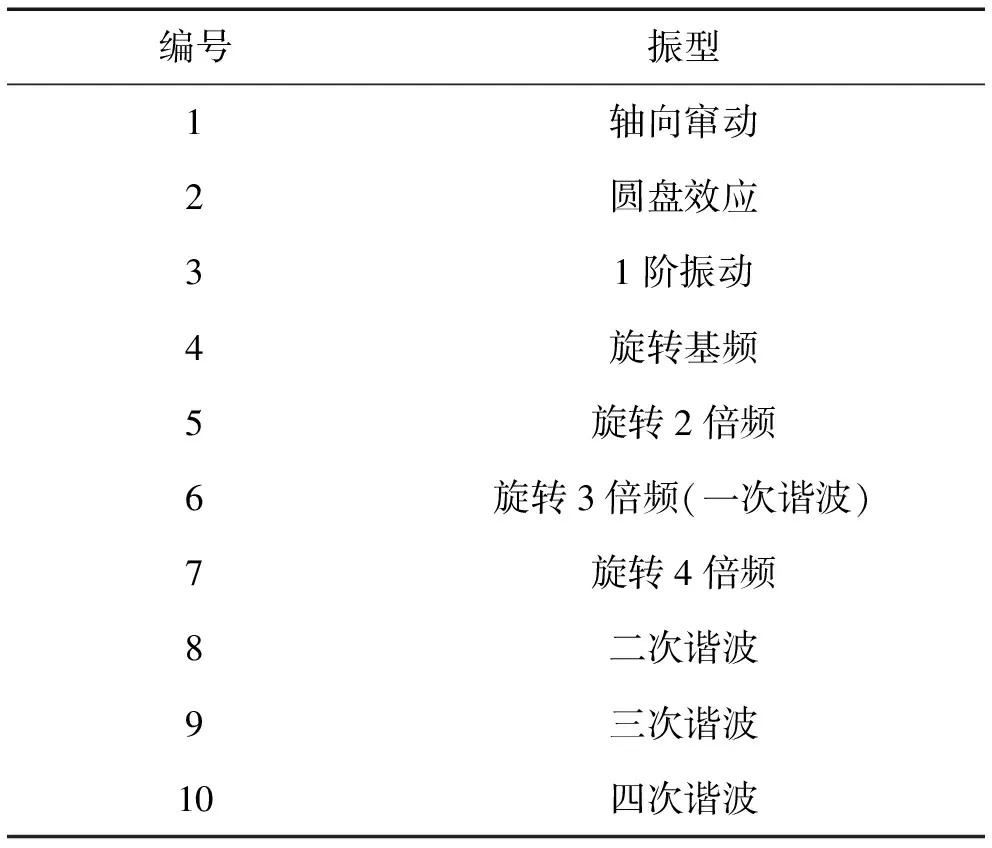
表2 振型参照表

(2) 定义λ为尖速比，Vib为振动频率，Pow为流场脉动频率。如表3、4所示，风速11 m/s，对比不同尖速比下，振动频谱与功率谱中对应峰值频率之间的相对误差δ=Δ/L×100%，Δ=|Vib-Pow|，L=Vib，得到δ<8.2%，对应关系较好。图7(a)所示，尖速比为4.5时，由于旋转基频与轴向窜动频率相近，故轴向窜动被旋转基频淹没。而对于能量谱中某些固有频率缺失可能是由于能量传递过程中的耗散或被淹没造成的。

表3 λ=4.5频率参照表

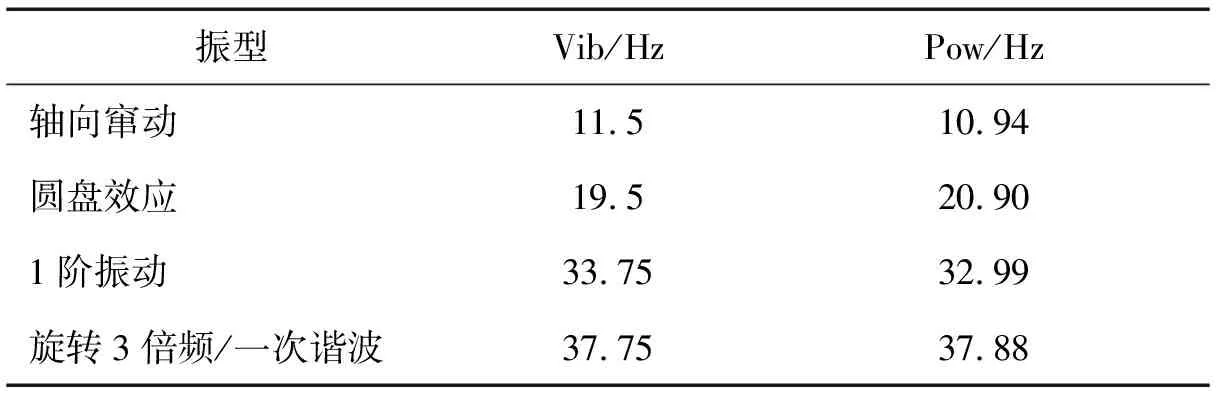
表4 λ=5频率参照表

(3) 若将功率谱中150 Hz以内能量峰值相加作为总和M，某振型对应的能量值为P，则通过该振型占总能量的百分比η=P/M×100%分析能量值的大小。由旋转三倍频产生的尾流一次谐波能量占尾流总能量的50%以上，故风轮转动产生的倍频振动是造成整体尾迹能量升高的最主要原因。

2.2 偏航对流固间关联性的影响分析

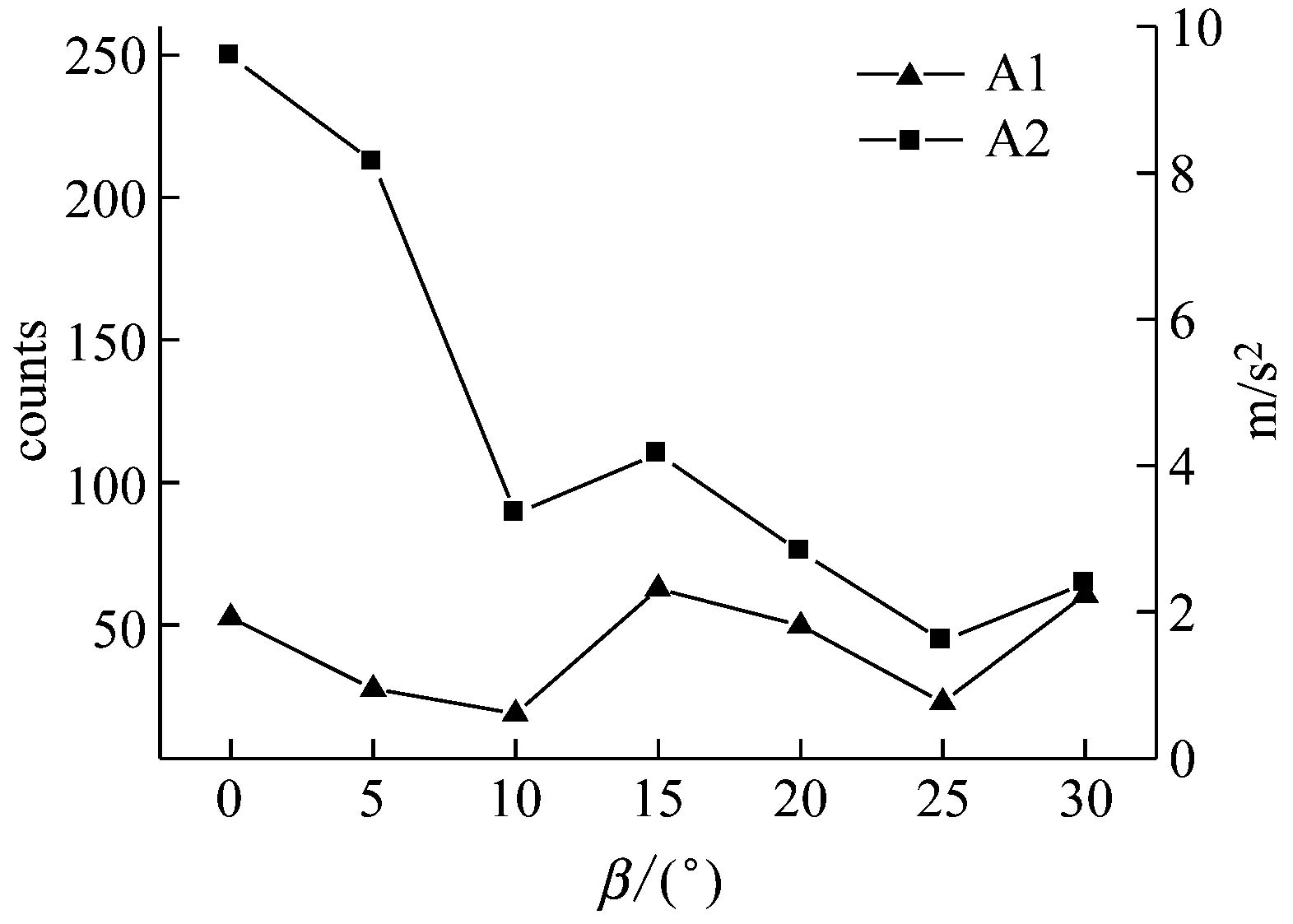
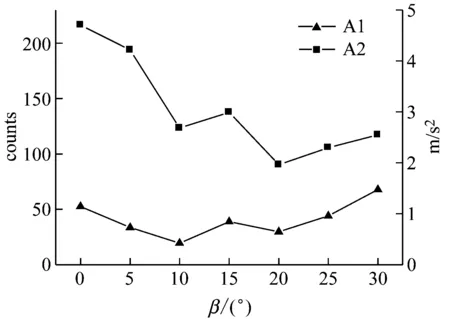
由上述分析可知，尾流能量集中于一次谐波，为了进一步探究偏航条件下叶片振动与尾流发展的关联性，提取不同偏航角下风轮旋转三倍频的加速度值与一次谐波的能量值，构建加速度值(m/s2)与能量值(counts)随偏航角的曲线图，如图8所示。

(a) 尖速比为4.5

(b) 尖速比为5

定义：A1为加速度值随偏航角变化曲线；A2为能量值随偏航角变化曲线。

通过对比图8中各分图，首先发现随着偏航角的变化加速度与能量值的变化趋势相同，风力机偏航条件下，风轮振动能量依然传递到了流场中；加速度曲线与能量值曲线之间的间距代表着风轮振动与尾流流体间相互作用的程度，发现偏航角小于10°时，叶片振动对风轮后流场的影响较大，风轮振动加速度值的微小变化，会引起流场能量值发生较大的幅值波动。而随着偏航角的增加，当偏航角为15°时，风轮虽然处于最恶劣偏航角，受到最大偏航激振力，振动加速度值增大，但由于尾流的偏斜与膨胀，外部主流区的流体与尾迹湍流发生掺混，尾迹的流动结构被破坏，并且偏航角增加后，叶片攻角增加，叶片表面流动分离逐渐扩大，进而使风轮的振动幅值对尾流的影响逐渐减小。

2.3 试验结果的可靠性及适用性分析

考虑到来流风况的特殊性，以相同的方法分析来流风速10 m/s与12 m/s，发现风轮振动与尾流之间同样存在密切关系，且具有随着偏航角的增加关联性减弱的特征。试验的工况中仅存在极个别的可忽略的微小差异，分析结果完全相同，可确定试验结果可靠。

由流体力学可知，若试验雷诺数的值比临界雷诺数Recr高，那么惯性力将远大于黏性力，因雷诺数不同带来的影响就可忽略。试验叶片为NACA翼型的改良加厚叶片，其临界雷诺数在105～106之内，已知，本文试验雷诺数大于临界雷诺数，故由风力机相似理论，对于完全相似的大风力机叶片，本文产生的试验结果同样适用。但当下大型风力机叶片多为玻璃纤维或碳纤维复合材料，叶片材质不同使得叶片在结构动力学特性方面存在较大差异，为了将理论研究与实际应用更加紧密的结合，下一步工作将对目前主流大型风力机模型进行测试研究。

3 结 论

(1) 提出了风轮振动信号与尾迹流场信息同步监测的方法，填补了相关测试方面的技术空白。

(2) 通过频谱响应分析，提出了以频率为纽带关联结构场与流场的新思路，以试验手段证明了风轮振动行为与尾迹流场确实存在密切关系；并发现风轮尾流脉动的主体能量为一次谐波。

(3) 对比风轮旋转三倍频与一次谐波幅值，发现加速度与能量值随偏航角的变化趋势相同，即使风轮发生偏航风轮振动与尾流间相互作用依然存在。并且偏航角小于10°时，尾流能量值对风轮振动加速度值的变化较为敏感，随着偏航角的增加，叶片表面流动分离以及外部流体与尾流掺混加剧，风轮尾迹结构遭到破坏，风轮振动与尾流之间的关联性减弱。

相关研究成果有可能为风轮及齿轮箱在远短于设计寿命期内频繁发生疲劳损伤事故提供新的解释，为风力机结构安全性设计、偏航控制方案的制定提供可借鉴的思路，同时为风力机流固耦合解耦方程的建立提供可靠的实验数据支持。