增量式监督局部切空间排列算法及齿轮箱故障诊断实验验证
2018-08-01田福庆梁伟阁
佘 博, 田福庆, 梁伟阁, 汤 健
(1.海军工程大学 兵器工程系,武汉 430000;2.北京工业大学 信息学部,北京 100124)
获取高维样本的低维嵌入子空间的降维方法在图像处理、故障诊断等方面得到了广泛的应用。LTSA作为一种非监督的流形学习降维方法,能有效提取高维样本的内在本质特征。在实际应用中,样本数据存在无标签信息和有助于识别分类的标签信息,而LTSA只能将所有样本作为无标签样本进行降维处理。在线监测机械设备状态应用方面,不断增加的状态数据对诊断算法的快速处理能力要求较高。LTSA作为一类批量处理降维方法,每次将新增样本加入到原始训练样本中,全部样本重新进行一次维数约简,而无法利用原始训练样本集降维的结果。随着动态数据的增加,批处理的方式耗时过长,不适合在线数据的处理。
监督学习能充分利用样本标签信息,增量式学习也能充分利用已获取的样本的低维嵌入结构,避免不必要的重复学习。监督流形学习方面,第1类方法通常是在样本k邻域选择中利用样本标签信息改进了样本间欧式距离矩阵,以确定样本更佳的近邻点[1];第2类方法是将监督算法与流形学习算法相结合[2],使得算法能处理样本标签信息。在增量流形学习方面,相关的研究方法主要有:第1类是线性化增量方法,如线性局部切空间排列(Linear Local Tangent Space Alignment, LLTSA)、迹比线性判别分析[3](Trace Ratio Linear Discriminant Analysis, TRLDA),以获取降维投影矩阵。第2类是基于标志点的增量学习,将标志点作为两个线性块的重叠点,利用重叠点在两线性块中低维嵌入坐标差值最小化原则,对新增样本低维坐标进行旋转、平移和缩放整合到原有样本中[4-5]。第3类是采用迭代的方法更新样本低维坐标,文献[6]对动态增加的全局坐标矩阵采用Rayleigh-Ritz法加速特征值的迭代计算,文献[7]迭代更新新增样本局部坐标矩阵,都是将高阶矩阵特征分解转化为低阶矩阵特征分解,降低了算法复杂度。第4类是采用最近邻近似方法,文献[8]提出利用新增样本最近邻点低维坐标线性估计新增样本点低维坐标。上述增量学习方法尚存在部分不足之处:①利用原有样本低维坐标获取新增样本低维坐标后,没有更新原有样本的低维坐标,随着新增样本的增加,新增样本与原有样本低维坐标间的差距会增大;②对新增样本的处理是逐个进行,不适合在线的数据处理。
本文提出一种增量式监督局部切空间排列算法(Incremental Supervised Local Tangent Space Alignment, ISLTSA),充分利用训练集中各类样本的标签信息,将散度矩阵融入LTSA算法中,构成监督LTSA流形约简方法(Supervised Local Tangent Space Alignment, SLTSA);对于批量增加的新样本,采用迭代的方法将动态增大的高阶全局坐标矩阵转化为低阶坐标矩阵进行特征值的计算,更新所有样本的低维嵌入坐标。将本文方法应用于齿轮箱的故障诊断中,并结合支持向量机SVM进行故障状态的识别。
1 增量式监督局部切空间排列算法(ISLTSA)
本文在改进局部切空间排列算法(LTSA)的基础上,分别提出了监督局部切空间排列算法(SLTSA)和增量局部切空间排列算法(ILTSA),结合以上两种改进算法形成ISLTSA算法。
1.1 局部切空间排列算法(LTSA)
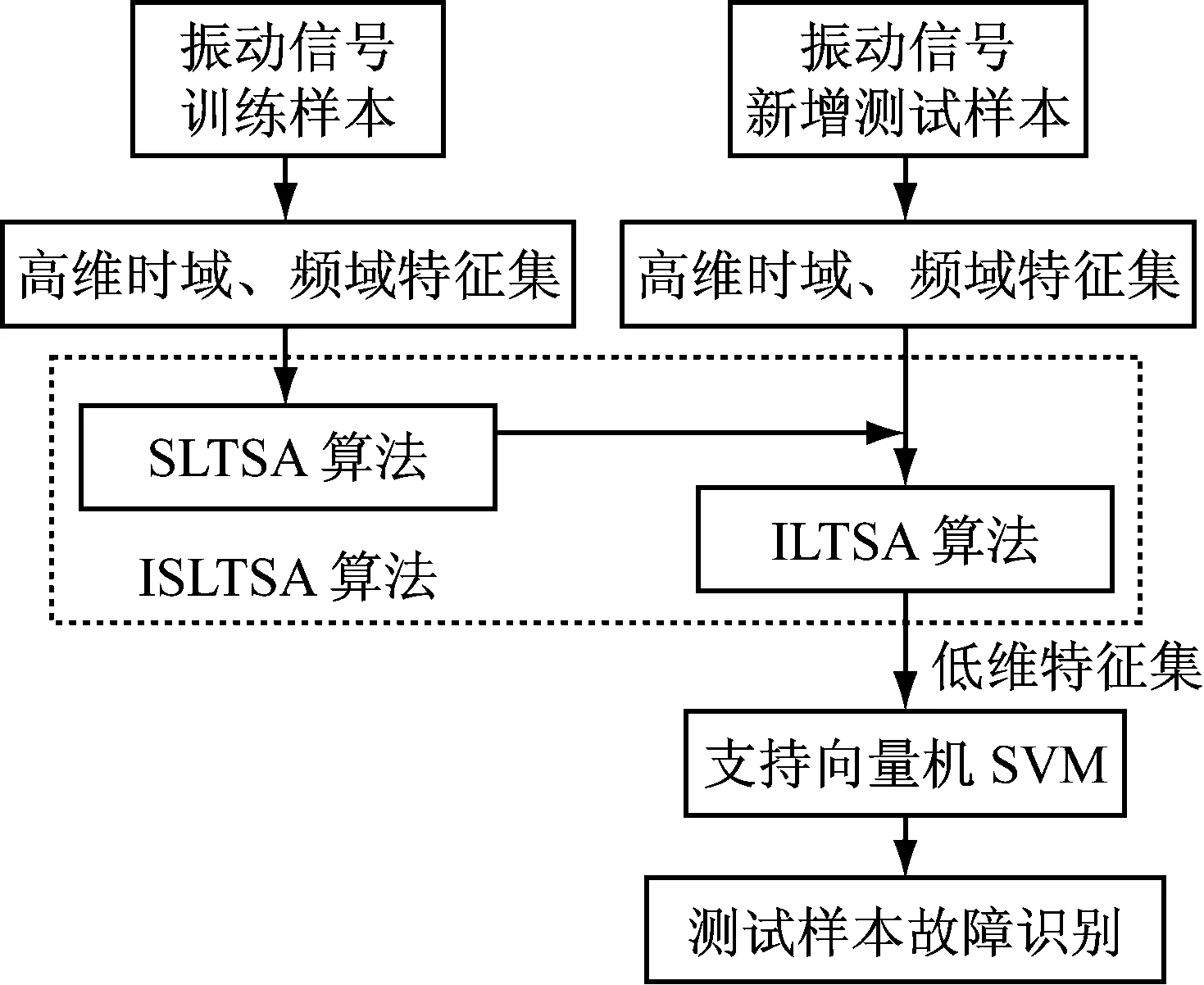
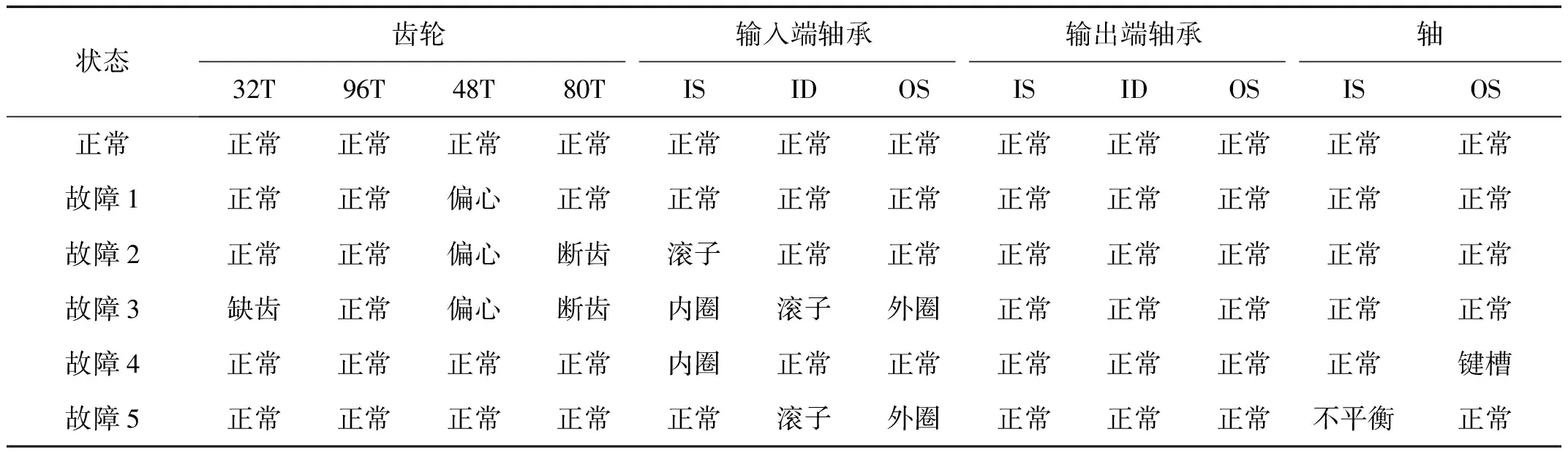
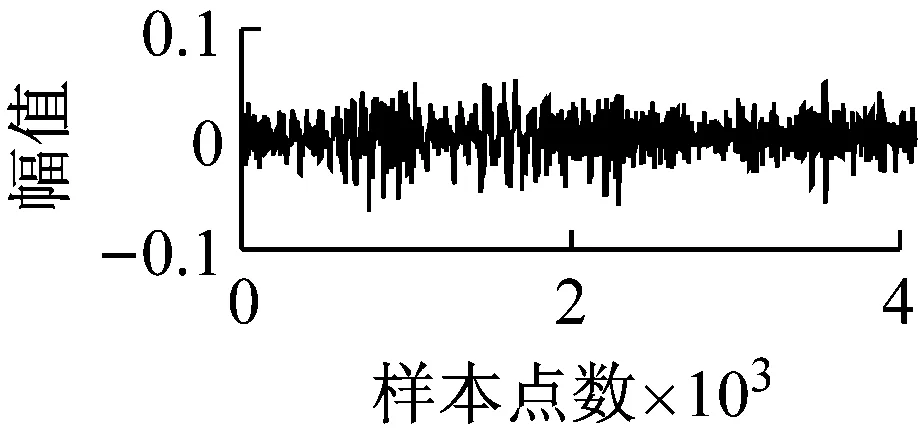
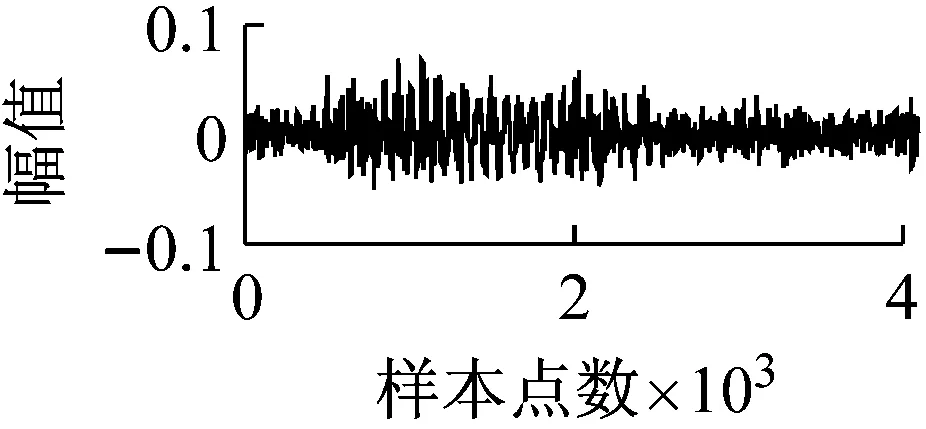
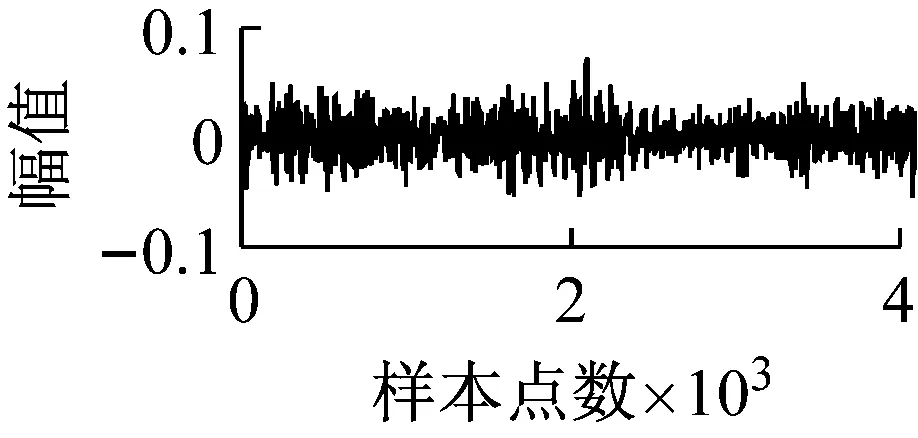
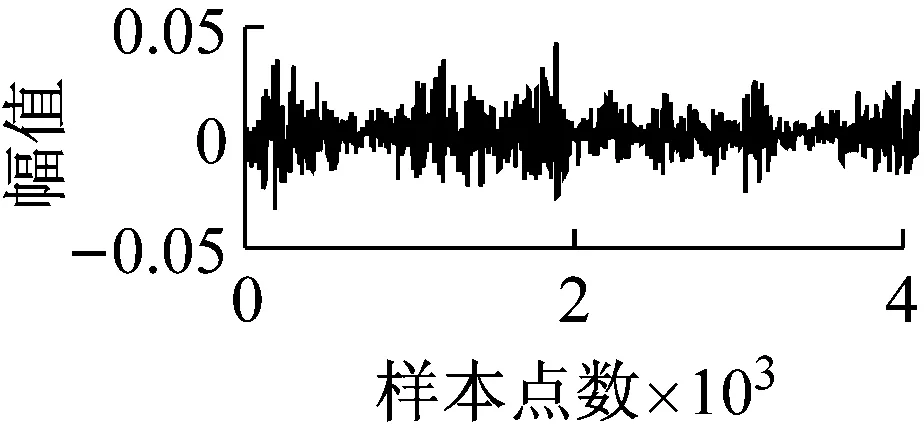
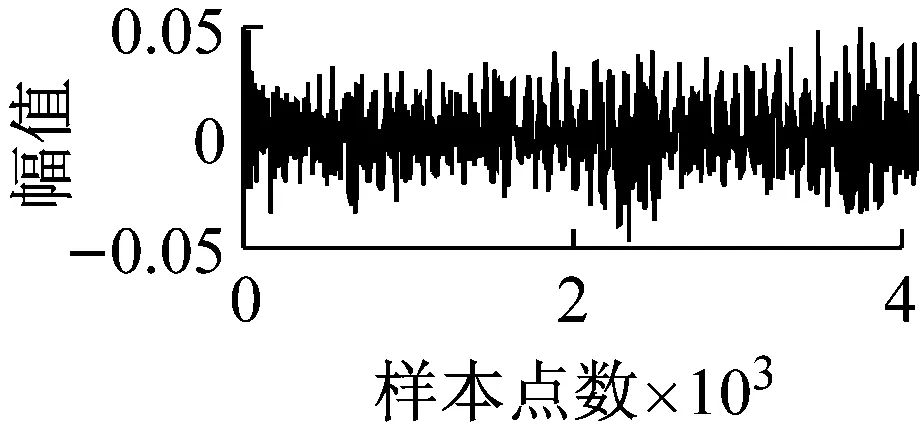
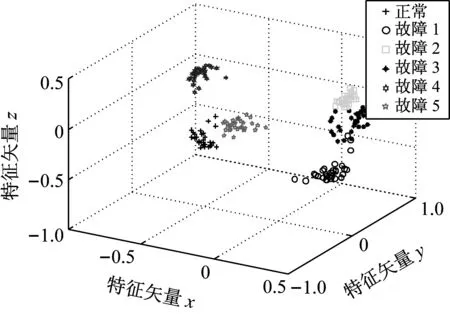
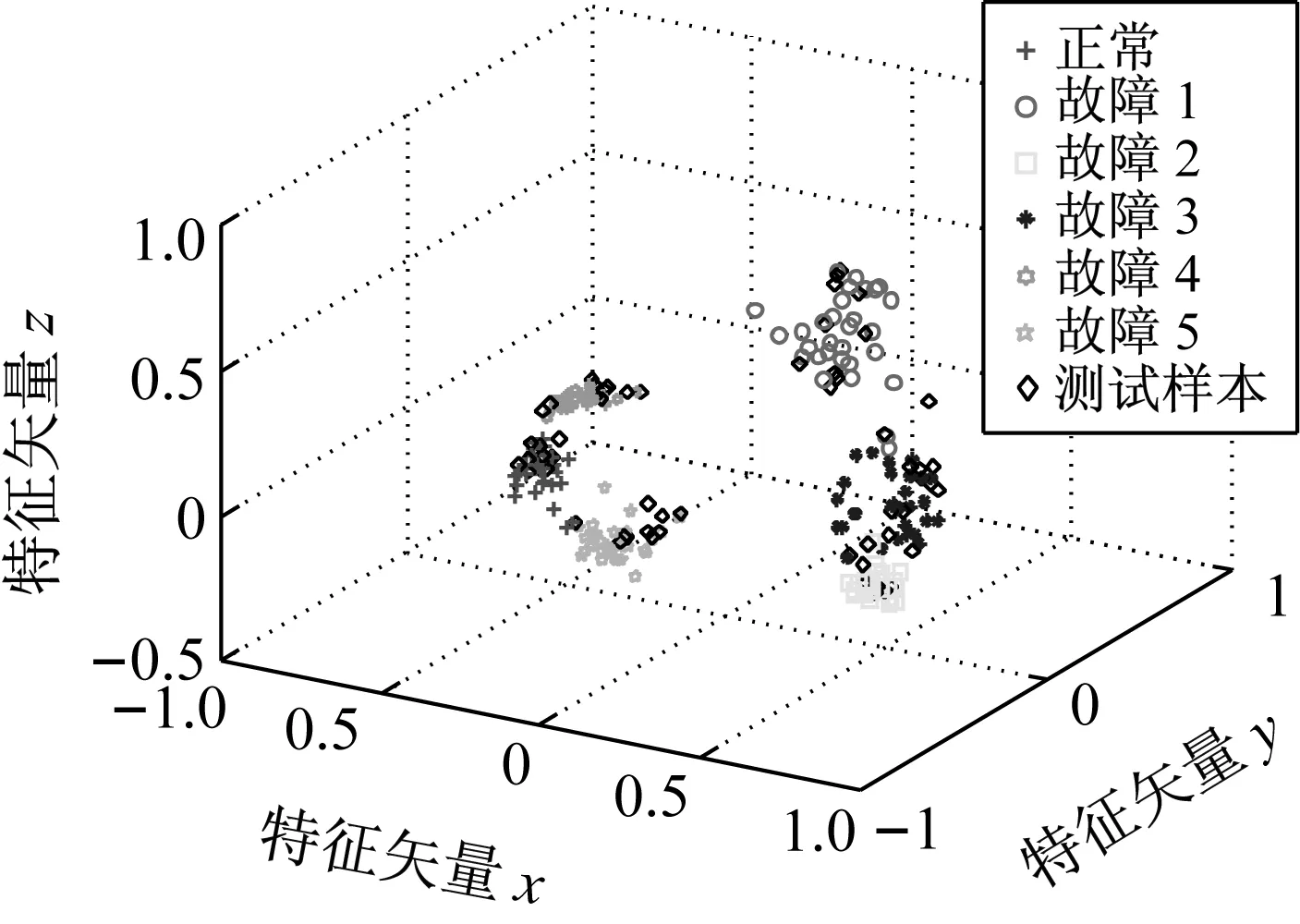
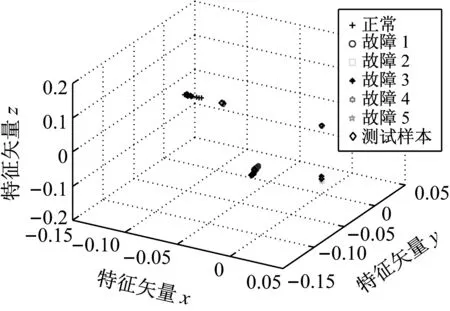
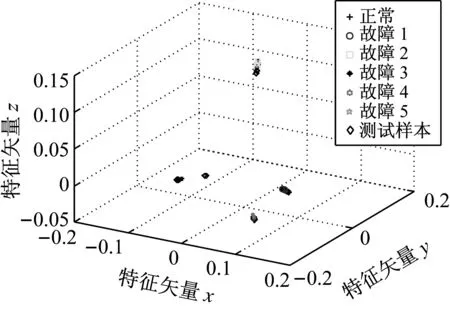
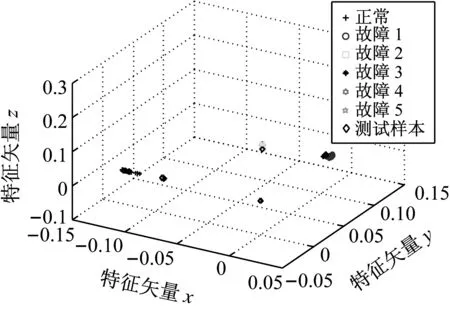
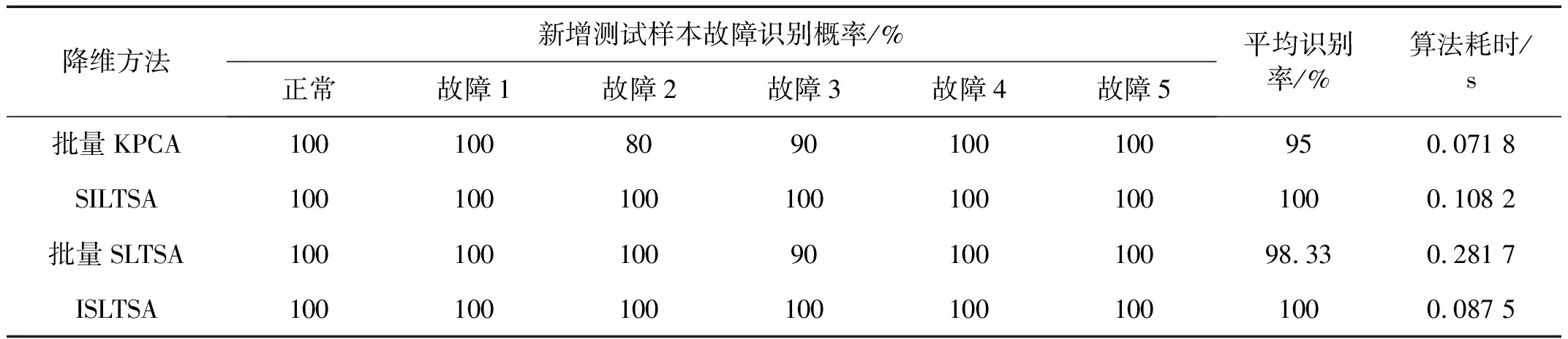
LTSA是基于切空间的流形学习算法,用近似的局部切空间来表示样本点所在流形的局部几何。将样本邻域中各数据点到局部切空间的正交投影在全局坐标系中进行排列,得到低维嵌入表示。LTSA算法将D维数据集X={x1,x2,…,xN}(xi∈RD)投影为d维数据集Y={y1,y2,…,yN}(yi∈Rd),d (1) 邻域选择。利用k-nearest neighbor近邻法,对给定样本集X中的每一个样本xi选择k个最近的样本(包括xi本身)构成局部邻域Xi=(xi1,…,xik)。 (2) 局部坐标拟合。对各局部邻域Xi,计算正交投影矩阵V使各样本到其投影的距离之和最小,即 (1) (2) (3) (4) LTSA算法在构建样本局部切空间中,将邻域内各点对切空间估计的贡献列为一致,而实际上,依据欧式距离进行邻域构造,各点对局部流形结构的贡献有差别[9]。采用权值wij反映邻域样本xij对切空间估计的贡献[10]。LTSA算法中局部坐标拟合的计算依据式(2)进行改进,如下: (5) LTSA是一种无监督学习算法,在实际应用中,数据集存在标签样本和无标签样本,充分利用标签样本进行训练,可提高得到的低维特征的可辨识性。线性判别分析(Linear Discriminate Analysis, LDA)是一种监督学习算法,其目的是使得原始空间中的类分辨信息在降维后在低维中依然得以保持,其中,类内散布矩阵Sw和类间散布矩阵Sb分别[11]为 (6) (7) (8) 既考虑高维数据的非线性结构,又考虑降维后低维坐标的判别特性,SLTSA算法的目标函数可进一步转换为 min tr(Y(αB+(1-α)(βLw+(1-β)Lb))YT) (9) 式中:参数α和β分别表示样本局部几何结构所占信息的比重和类内类间判别比重因子。 样本集X={x1,…,xN,xN+1,…,xN+L},前N个为训练样本,后L个为新增样本,新增样本加入数据集后,只改变部分训练样本的k近邻。定义近邻点变化了的训练样本点集合为XA,XA也包含了L个新增样本,IAi=(i1,…,ik)是XA中样本xi的k个近邻下标。全局坐标矩阵B更新如下 (1)对于样本集X中不属于XA的样本xj,Bnew(Ij,Ij)=B(Ij,Ij); (2)对于样本集X中属于XA的样本xi,初始化Bnew(IAi,IAi)=0,更新全局坐标矩阵 (10) 由更新的全局坐标矩阵Bnew计算新增样本低维坐标,目标函数如下 (11) (12) 将式(12)对YL求偏导,并使算式为0,有: (13) (14) 新增样本将改变部分训练样本的邻域,全局坐标矩阵Bnew也随之部分变化,当新增样本不断增加,难以直接对Bnew进行特征分解获取样本集的全局低维坐标。利用Rayleigh-Ritz迭代算法可加速特征分解,但一般文献中迭代初值的选择是直接采用训练样本的低维坐标和新增样本的低维坐标[12],实际上,新增样本的加入会使训练样本低维坐标发生轻微的改变。本文中对训练样本的低维坐标进行更新,并作为迭代初值,将式(12)对YN求偏导,并使算式为0,有: (15) 采用类似Rayleigh-Ritz的迭代算法[13]对全局坐标矩阵Bnew的特征值进行迭代计算,实现训练样本和新增样本的全局低维坐标的更新,迭代步骤如下 (2)由K·Zi=Qi-1,计算Zi; (3)对Zi进行QR分解,Zi=Vi·R; (4)令Vi=Vi(:,d+1),由(Vi)TK-1Vi=Ui∑(Ui)T计算Ui; (5)Qi=ViUi。 YN+L=Qi(:,2:d+1),即为更新后的全局低维坐标。由此,可将(N+L)×(N+L)阶的Bnew矩阵转化为(d+1)×(d+1)阶的矩阵分解,提高了计算效率。 假设样本集X={x1,…,xN,xN+1,…,xN+L},前N个为训练样本,后L个为新增样本,计算新增L个样本的全局低维坐标Yi(i=1,…,L),ISLTSA算法描述如下 步骤1:依据SLTSA算法,由式(9)对矩阵αB+(1-α)(βLw+(1-β)Lb)进行特征分解,得到N个训练样本的全局低维坐标Yi(i=1,…,N); 步骤2:依据ILTSA算法,对于新增L个样本,由公式(11)更新全局坐标矩阵Bnew; 本文选取齿轮箱振动信号11个时域特征(均值、峭度、均方差等)和13个频域特征(均方频率、频率方差、重心频率等)组成高维特征集[14]。故障诊断实现过程如图1所示,具体步骤为 图1 齿轮箱故障诊断流程 (1) 采集齿轮箱不同状态的原始振动信号作为训练样本,利用时频分析提取高维特征,并使用SLTSA算法获取低维嵌入坐标。 (2) 将齿轮箱状态监测过程中获取的振动信号作为新增测试样本,提取高维特征,并使用ILTSA算法获取低维嵌入坐标。 (3) 使用支持向量机进行故障模式识别,判断齿轮箱状态。 选择IEEE PHM Challenge[15]的齿轮箱振动数据,齿轮箱结构如图2,部分齿轮故障如图3所示。在齿轮箱输入轴和输出轴分别安装振动加速度传感器,采样频率为66.67 kHz,输入轴转速有五种工况,每种转速下又分为高负载和低负载两种工况,每种工况下有8种不同的状态。本文选用3 000 r/min、低负载下齿轮箱输出轴端的振动信号进行故障诊断,取6种不同状态的振动信号,由单一故障或多类故障组成,如表1所示。其中,32T、96T、48T、80T分别表示输入轴齿轮、中间轴齿轮1、中间轴齿轮2、输出轴齿轮,IS、ID、OS表示输入轴、中间轴、输出轴。各状态下的齿轮箱振动信号选取30组作为训练样本,每组采集4 096个数据点,另外,每种状态分别取10组数据作为新增测试样本。 图2 齿轮箱结构图 图3 齿轮故障:正常、缺齿、断齿 齿轮箱在不同故障状态下振动信号如图4所示,分别提取时域、频域的24维特征,为便于可视化,选取低维子空间的维数d=3,另外,本文所应用到的流形学习算法在构建局部邻域中均选取k=8。对于训练样本,分别采用KPCA、LTSA、SLTSA算法进行维数约简,三种方法的低维嵌入坐标分别如图5、6、7所示。其中,在SLTSA监督局部切空间排列算法中有两个参数α、β,结合支持向量机SVM优化故障识别概率进行参数选择,本文设置α=0.7,β=0.6。对于新增测试样本,分别采用批量KPCA、SILTSA、批量SLTSA、ISLTSA四种增量维数约简方法,低维嵌入坐标分别如图8、9、10、11所示。其中,批量KPCA和批量SLTSA都是将新增样本合并至训练样本进行降维;SILTSA也是监督增量LTSA算法,监督算法采用文献[1]中由样本标签重新定义样本间距离进行邻域的选择,新增样本局部低维坐标计算也采用文献[1]中由近邻点全局低维坐标进行加权,训练样本和新增样本全局低维坐标的更新采用本文的迭代方法;ISLTSA是本文提出的增量监督LTSA算法。 表1 齿轮箱故障状态 (a) 正常 (b) 故障1 (c) 故障2 (d) 故障3 (e) 故障4 (f) 故障5 由表2所示四种增量降维方法的故障识别率和算法所耗时间。文中仿真是在Windows7操作系统、Core i5-4590(3.3 GHz)环境下进行。批量KPCA方法耗时最少,但故障识别正确率最低。SILTSA和本文的ISLTSA方法故障识别正确率高,表明了充分利用样本标签能提高辨识度,相对于批量SLTSA算法,本文提出的增量方法耗时少,能减小算法复杂度。 图5 KPCA降维结果 (16) 图8 批量KPCA降维结果 Fig.8 Processing result of testing samples by KPCA 图9 SILTSA降维结果 图10 批量SLTSA降维结果 图11 ISLTSA降维结果 降维方法新增测试样本故障识别概率/%正常故障1故障2故障3故障4故障5平均识别率/%算法耗时/s批量KPCA1001008090100100950.071 8SILTSA1001001001001001001000.108 2批量SLTSA1001001009010010098.330.281 7ISLTSA1001001001001001001000.087 5 表3 各降维算法聚类度 如表3所示,SILTSA、批量SLTSA、ISLTSA算法的聚类度较小,KPCA聚类度大,结合图9、10、11和图5、6进行对比,KPCA、LTSA降维后样本坐标类内散度大,ISLTSA降维后样本类内散度小,也表明了本文提出的监督降维方法能取得较好聚类效果。 本文提出了一种新的增量监督局部切空间排列算法ISLTSA,在原始LTSA算法目标函数中融入了类内散度和类间散度矩阵,充分利用标签样本,使得低维嵌入坐标同类聚集、异类分离,将初步更新的训练样本低维坐标和新增样本低维坐标作为初始值,采用迭代的方法更新所有样本全局低维坐标,既能获取准确的高维样本低维嵌入坐标,也能降低维数约简的算法复杂度。通过与其它增量式降维算法对比,采用齿轮箱的故障数据验证了本文所提出算法的高效性,适合在线监测机械设备状态。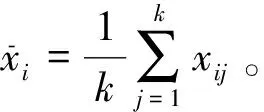
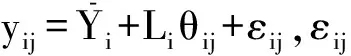
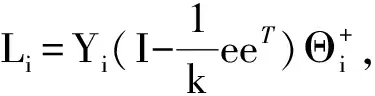
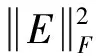
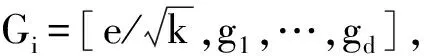
1.2 监督局部切空间排列算法(SLTSA)
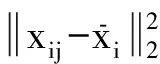
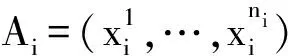
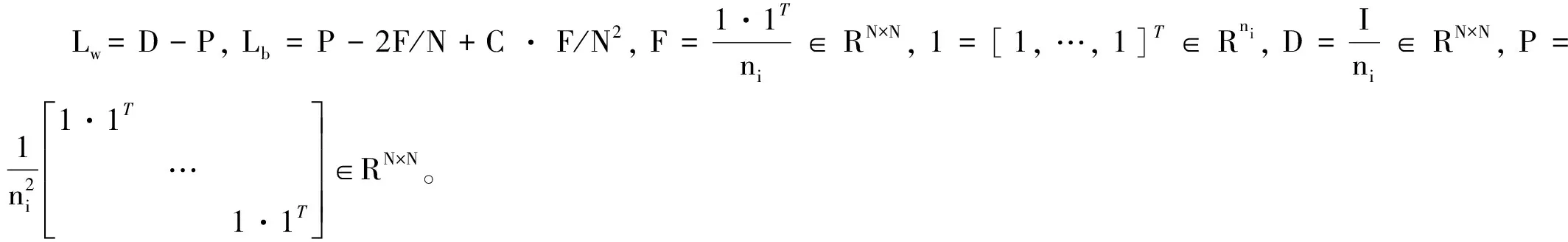
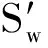
1.3 增量局部切空间排列算法(ILTSA)
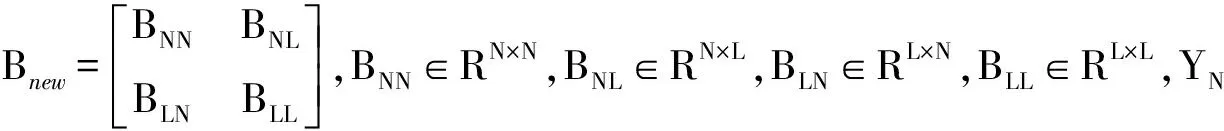
1.4 增量式监督局部切空间排列(ISLTSA)算法步骤
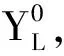
2 基于ISLTSA算法的齿轮箱故障诊断实验验证
2.1 齿轮箱故障诊断流程
2.2 实验数据


2.3 结果分析


3 结 论
