面向加工中心床身的改进BP神经网络优化系统

刘斯妤,史安娜,曹富荣,马晓波

(1.沈阳理工大学 机械工程学院,沈阳110159;2.沈阳机床集团,沈阳 110142)

智能机床的高速发展对机床提出了越来越高的要求,机床床身的进给系统为工件加工提供往复移动的作用,因此其动态特性对整机的加工精度影响很大[1-3]。采用有效的方法对机床的进给系统进行优化,对智能机床加工精度的提高有重要意义。

结构的优化设计可以归结为一个轻量化问题,通常以结构的质量为目标,结构的动静态特性为约束条件,对质量的最小化进行寻优。文献[4]建立了机床的动态模型并基于结合面进行了拓扑优化。文献[5]对机床进行了轻量化设计,并通过改变筋板的布局进行尺寸优化。文献[6]对加工中心的横梁进行了优化设计,在分析出薄弱部位的同时,对进给机构中重力、外力的作用以及轴承部位热的作用进行考虑。当今学者对机床进给机构的研究,通常没有考虑进给机构结合面的刚度作用,难以准确获得性能最优的结构优化方案。

本文以智能机床i5系列M4.5机床的床身进给系统为研究对象,在充分考虑其结合面特性的基础上,建立多软件的协同优化平台,形成一个智能机床进给系统的遗传算法和神经网络优化系统。在常规优化的基础上,采用灵敏度分析法、神经网络和遗传算法相结合,进行多目标优化,从而提高进给机构的动态特性。

1 进给机构的优化系统模型

机床进给机构的设计包括需求分析、部件结构设计、参数化建模、动态特性仿真及多目标优化等[7]。因此,本文构建由需求分析模块、部件结构设计模块、参数化建模模块以及优化模块组成的智能机床的优化系统模型,总体结构如图1所示。

图1 智能机床的优化系统模型

2 优化系统模型的构成与运算

2.1 需求分析模块

需求分析模块获取机床用户的主要需求,包括材料特性、零件间的约束条件和进给速度[6]。该床身进给机构的最大进给速度为0.9m/s,系统根据输入的需求参数计算机床的进给功率等,最终得知机床的总体结构。

2.2 部件结构设计模块

智能机床的床身进给系统的设计包括床身的零件尺寸、轴承类型、轴承刚度、丝杠类型、螺母预紧力、丝杠预紧力大小等,根据装配后的位置关系,对结构进行刚度、强度的校核,得出床身进给系统的部件结构。

2.3 优化模块

根据部件结构设计模块得到的参数,对床身进给结构在Solidworks软件中创建三维模型,通过导入功能导入到Ansys软件中,结构的材料如表1所示。为准确模拟结合面的接触情况,建立进给机构结合部的动力学模型。该进给机构中的固定结合面为螺栓结合面,即8个地脚螺栓与地面进行固定,床身的质量为800kg,地脚螺栓为高强度螺栓,螺栓的强度等级为10.8级,螺栓的拧紧力矩为2200N·m。

表1 结构材料参数

通过计算结合面上的平均接触压力,可以将结合面简化为一个结点G。利用吉村允效积分法计算出G点各方向上的等效弹簧刚度分别为

K1,2=αPnβΔS

(1)

Kx=∬K1Pndxdz=Kz

(2)

Ky=∬K2Pndxdz

(3)

式中:Pn为分量作用力;ΔS为接触面积;K1、K2为刚度值;α、β为与结合面的材料、加工方式等因素相关的值,α=1110430;β=0.863。

根据简化刚度计算结果,将刚度值施加在床身的中心处,准确模拟结合面的刚度,其他固定结合部计算结果如表2所示。

表2 固定结合部刚度值 N/m

滚珠螺旋传动系统是由螺母、丝杠和滚珠等组成,而系统的刚度由定位精度和传动精度决定,刚度越高,传动的精度越高。丝杠在工作时受轴向力、重力和扭转变形的作用,因此该系统采用两端固定的支撑方式,如图2所示。

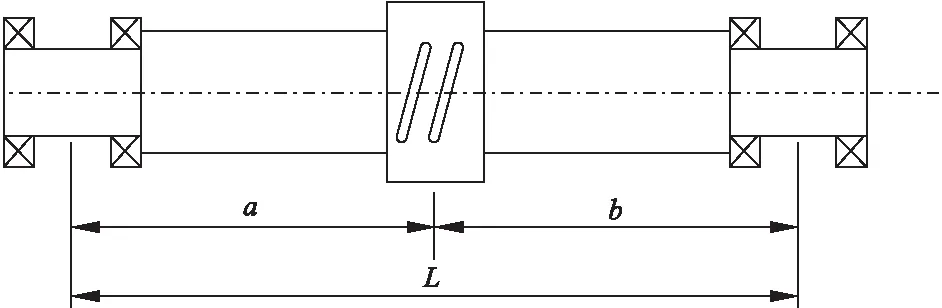
图2 丝杠的支撑方式

计算该丝杠的刚度

(4)

式中,P为工作载荷,δ为弹性变形量。

轴向的变形量为

(5)

(6)

式中:δ1为丝杠轴向位移;a、b为螺母至两端支撑的距离;d1为丝杠螺纹内径;E为弹性模量,K1为轴向刚度值。

当a=b时,K1取得最小值

添加有限元模型的边界条件,丝杠添加轴向的弹簧刚度值490N/μm,床身下方采用地脚螺栓进行固定,对地脚螺栓添加弹簧刚度值,精确的模拟床身与底面之间的连接形式,最后提交到运算器中进行求解。

考虑到加工精度和整机的动态特性,在满足机构进给行程情况下,以机床进给系统的质量、一阶固有频率和静变形为目标函数,进行多目标优化[8]。由于进给机构的尺寸变量较多,选择设计变量时,通常先对机构进行灵敏度分析,找出关键参数作为设计变量。根据灵敏度分析的结果,床身内部x方向的筋板厚度x1、y方向的筋板厚度x2及床身的厚度x3对静、动态分析结果有很大影响,因此选择这3个变量为设计变量。

2.4 神经网络-遗传算法寻优

由于传统的数学计算方法难以求解神经网络,而BP神经网络(Back-Propagation Network)是对非线性函数进行权值训练的网络,且结构简单,计算速度快,可以较为便捷的解决多目标优化问题,因此采用BP神经网络通过神经元之间的连接阈值和权值建立映射关系[9]。由于求解神经网络过程中计算量较大,因此对于床身影响较大的三个尺寸参数可以建立其与一阶固有频率、总质量和静变形的关系,进行样本点的学习。

通过采集动静态分析的样本数据,建立关键尺寸与固有频率之间的非线性映射关系。设置BP神经网络训练过程中最大训练次数为9000次;选择遗传算法优化时,设置其种群规模为80、最大进化代数为8900。繁殖后代得到新的种群并采用遗传算法优胜劣汰,经过迭代运算,寻求最优解,具体数据如表3所示。

前50组为训练数据,即对权值和阈值进行修正,直到收敛为止,50～60组为测试数据。将以上数据导入到BP神经网络中进行模型建立,将训练误差设置成10-5,使精度足够高。测试后,得到准确的神经网络模型。

考虑到床身的固有频率和质量的影响,在表3中选取最优解,得到最终的优化结果。针对智能机床床身的优化系统运算过程如图3所示。

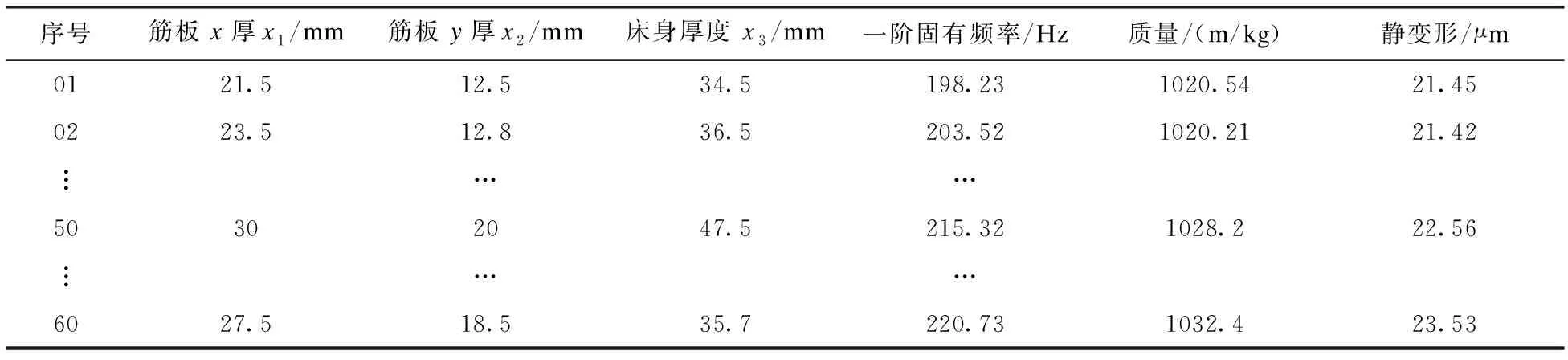
表3 BP神经网络训练、测试数据

图3 智能机床床身的优化系统运算

根据有限元仿真结果,建立进给机构的多目标优化模型,床身进给机构多目标优化的数学模型为

(7)

式中:xi为设计变量;F(x)为目标函数;gu(x)、hv(x)为约束函数和等式约束函数;xil、xim为设计变量的上限和下限。

以BP神经网络训练获得的模型为依据,建立目标方程,用Matlab中的GA工具箱进行求解,寻求最优解(将最优解的数值保留两位小数),为获得更为准确的优化模型,将最优值代回到Ansys Workbench中,分析结果,得到优化前后尺寸参数及固有属性的变化[10]。求解后将数据储存在数据库中,按照前面静态分析、模态分析的方法对优化后的机构进行分析比对,如表4所示。

表4 优化前后尺寸参数的变化

优化后机床床身固有频率提升、质量降低,且静变形量减小。证明该机床床身动态特性提高,抗振性得到提升,验证了该智能机床优化系统的有效性。

3 结束语

针对智能机床的进给机构建立了一种多学科优化系统,利用吉村允效法建立结合面的动力学模型,相比虚拟材料法处理结合面,结果更为准确;采用神经网络、遗传算法相结合的方式进行寻优,不但大大减小了计算时间,且使寻优结果更为准确,最终通过实验验证了该系统的可行性。该系统的优化设计模块,可以较为清晰的进行优化设计计算,解决了数据与拓扑关系丢失的问题,实现了优化设计信息的资源共享,提高了智能机床的精度和水平。