一种锥规化的近似解法
2018-08-01顾世煜
李 扬,顾世煜
(1.沈阳理工大学 理学院,沈阳 110159; 2.东北中山中学,沈阳110001)
锥规化是一种特殊的凸规化,是线性规划的推广,是在一个仿射空间和一个正则锥的交集上,求线性目标函数的极大或极小值。锥规化问题涵盖了线性规划、凸二次约束规化、半正定规化、二次锥规化。近些年,由于锥规化理论和算法的发展,且在投资组合优化、最小风险套利、协方差矩阵的逼近等方面有广泛的应用,因而锥规化是数学规划领域的一个活跃的研究方向。锥规化问题是NP难问题,这种问题没有一个多项式时间的算法。Bomze等[1]尝试用可行下降法对锥规化求解,然而这种方法无法证明解的收敛性,并且需要额外的工作去找出一个可行的起始点,而找可行起始点的难度不亚于解决原问题。Zilinskas[2]使用一种单纯形划分的方法去解锥规化问题的对偶问题,但模型求解的运行时间过长。Deng等[3]将锥规化问题近似转化为一个二次规化问题,然后利用在椭球域上的非负二次函数定义的对偶锥,解一个线性锥规化序列,得到原问题的近似解。以上研究得到的近似解要么计算繁琐,要么得到解的近似程度不高。
本文引入建立在集合FSOC上的一种非负二次形式锥,利用一系列的非负二次形式锥近似计算一种有用的NP难锥规化问题,是利用对一种标准单形的划分去逼近对偶锥的方法,根据半正定规化的解法,得出NP难锥规化问题一个比较好的下界,进而得到原问题的一种近似解。随着对标准单形的分割越来越细,同时逼近锥规化问题(P)下界的误差也越来越小。
1 基本概念
给定集合S⊆Rn,在S上的非负二次形式的锥定义为
CF={M∈Sn|xTMx≥0,∀x∈F},
式中Sn是n阶实对称矩阵,其对偶锥[4-5]是
式中,cl表示闭集,Cone表示集合的锥包。
一种标准的锥规化[2]的形式如下:
minf(X)=D·X
s.t.Ai·X=bi,i=1,2,…,m,
(P)
X∈C*
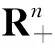
锥规化在二次规化和组合最优化中非常有用[6],Burer[7]证明了带有线性和0-1约束的二次规化问题都可以改写为锥规化模型(P),许多组合最优化也都可以转化为模型(P)问题,但模型(P)是NP难问题,即不能在多项式时间找到最优解,这就需要找到其近似解。
2 基本性质
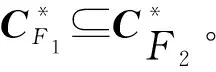



定理2设F⊆Rn是闭凸集,则CF=CCone(F)。


定理3对于上述定义的二阶锥FSOC和GSOC,有FSOC=Cone(GSOC)。

由定理2与定理3的结果,显然有以下推论:
推论 对于上述定义的二阶锥FSOC和GSOC,有CFSOC=CGSOC。
3 锥规化模型(P)的近似解


(AP)



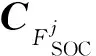
假设标准单形Δ划分为Δ=Δ1∪Δ2…∪Δk,那么(AP)模型可改进为:
(APP)
此问题的对偶问题如下:
(DAAP)

4 结束语
本文建立在集合FSOC上的一种非负二次形式锥,利用一系列的非负二次形式的锥近似计算一种有用的NP难锥规化问题(P),利用对标准单形的划分去逼近对偶锥,根据半正定规化的解法,得出这种NP难锥规化问题的一个比较好的下界,进而得到原问题的一个近似解。对于模型(APP),随着分割步骤的反复进行,标准单形Δ被分割的越来越细,同时逼近锥规化问题(P)下界的误差也越来越小。更好的逼近原来锥规化问题(P)的近似解。
