基于分簇的近似KNN的查询优化算法

黄 月

(沈阳理工大学 自动化与电气工程学院，沈阳 110159)

数据查询是无线传感器网络(Wireless Sensor Networks,WSN)研究的重要内容之一。由于传感器网络分布在较大的监测区域内，因此会产生大量的分布式数据，且节点资源非常有限，查询过程将消耗大量的能量，因此研究高效的数据查询方法将会提高网络的生存时间[1-3]。

K近邻(K-Nearest Neighbor)查询即查询距离给定查询点最近的K个对象，在WSN中K近邻查询的查询结果不仅取决于单个节点的数据，而且还与其他节点的数据有关联，因此，K近邻查询属于传感器网络中的复杂查询问题[4]。传感器网络的数据查询可以分为基于位置的查询(location-based query)和基于数值的查询(value-based query)。基于位置查询的目标是查询相关空间位置上及其周围节点的信息；基于数值查询的目标是查询某一数据及其周围数据的信息。基于位置的查询获得较多研究成果：Yingqi Xu等[5]提出GRT算法，利用节点的空间信息建立全局树结构进行查询。J.Winter等[6]提出KPT算法，该算法利用节点之间互相通信建立近邻信息，然后通过广播通知通信半径内的节点上传k-1个信息，该算法不需要建立检索结构，算法适用性较强。Yingqi Xu等[7]提出IWQE算法，该算法采用地理路由协议，首先在查询范围内选择查询节点，查询节点负责广播查询请求，当查询节点收到采集信息后，将信息与查询请求发送至下一跳的查询节点。由于传感器网络的数据分散且数据相关性较大，基于数值的查询大都集中在Top-k[8]研究，因此研究基于数值的KNN查询具有较高的实际和理论意义。Yongxuan Lai等[9]提出KVC算法，首先根据节点测量的数据进行分簇，然后在簇内选择存储节点，该算法将数据在网内进行处理，减少了数据的通信量，但当网络的数据较分散时，效果变差。李斌阳等[10]提出基于过滤器的近似一维KNN查询优化算法(FAKNN)，该算法利用经验值作为过滤器，通过过滤器阻止无效数据的发送，从而节省节点能量。

本文提出一种基于分簇的近似KNN查询优化(Approximate K-Nearest Neighbor Based Clustering——CAKNN)算法，提出基于位置、数据的分簇算法，该算法将测量数据值及物理位置接近的节点分为一簇，因此会减少数据传输跳数，降低节点能量的消耗，但当地理位置较远的节点测得相近的数据时，会导致簇与簇之间测量数据的范围产生重叠，基于数据离散度的查询算法，通过簇头节点报告的信息，基站可以确定查询存储节点的数量及查询个数，从而解决簇之间测量范围重叠的问题。整体算法可以分为初始化阶段和查询阶段。

1 查询系统的建立

本文基于以下假设：

(1)传感器网络中存在三类节点：基站、存储节点和采集节点。在网络初始化阶段基站负责接收数据、对节点进行分簇及选择存储节点，并广播每个存储节点的测量范围，在查询阶段基站负责发送查询指令；存储节点具有较大的存储能力。

(2)查询阶段，采集节点以固定频率采集数据，并将数据传送给存储节点，若存储节点的测量范围与其他存储节点的测量范围产生重叠，则存储节点向基站发送更新报告，否则不发送。若基站接收到存储节点的更新报告，则重新进行分簇及存储节点的选择。

(3)在较小的时间间隔和区域内，节点的监测信息具有相似性，即监测信息变化较小。

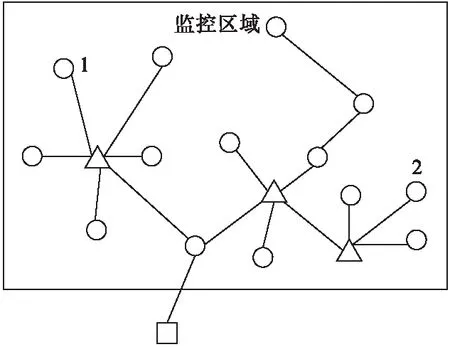
图1 查询系统结构图注：○传感器节点；△存储节点；□基站。

1.1 LVC算法

由于传感器节点广泛分布在较大的监测区域内，若两个节点的测量数据值比较接近，但位置相距较远(如图1节点1和节点2所示)，只考虑测量数据进行分簇(如K均值分簇)，则簇与簇的测量范围不会产生重叠，即将簇的测量范围从小到大依次排列得到[lb1,hb1],…[lbm,hbm]，则lbk≥hbk-1,(k=2,…,m)。但可能将两个相距较远的节点分在一个簇内，当节点向存储节点传送数据时会消耗较多的能量。本文提出一种基于位置-数据的分簇(Location-Value Clustering,LVC)算法。

算法伪代码如下所示：

LVC算法伪代码初始化:N个节点,分簇的数量为Cluster_num-1。while (有两个以上的簇测量范围重合)Cluster_num=Cluster_num + 1;为每个簇任意分配一个节点Cluster(i)={NVi}。while (簇的集合发生变化)计算每个簇的测量中心CVCi=∑mj=1valuej计算每个簇的位置中心CLCi_X=∑mj=1xj CLCi_Y=∑mj=1yjfor i=1:N 计算节点i到每个簇测量中心的距离Dist_Value( j ); 计算节点i到每个簇位置中心的欧氏距离Dist( j ); MaxDist=Max(Dist); 若Dist(t)

1.2 存储节点的选择

当传感器网络分簇完成后，基站根据每个簇包含的节点集合及节点的测量值建立簇的参数矩阵[cid,sp_id,size,mean,var,lb,hb]，cid为簇的ID号；sp_id为该簇存储节点的ID号；size为簇内的节点数量；mean为该簇测量值的均值；var为该簇测量值的方差；lb为该簇的测量下限；hb为该簇的测量上限。设簇i的集合为Clsteri={NV1,NV2,…,NVm}，用线性规划模型确定存储节点：

(1)

sp∈Clusteri,NVi∈Clusteri,

dist(NVi,sp)即为节点i到存储点sp的欧式距离。

当簇内节点的查询数据发生变化但簇之间的测量范围没有产生新的重叠，即lbk≥hbk-1,(k=2,…,m)，簇头仅向基站报告新的均值和方差，不用报告每个节点的变化情况，因此可以降低能量消耗，延长网络生存时间。若簇之间的测量范围产生新的重叠，则重新分簇。由于存储节点需要不断监听网络状态，因此要消耗较多的能量，可以周期性选择存储节点周围的节点作为新的存储节点。

2 查询处理

当查询指令[qv,k]到达后，基站根据簇头的数据特点〈cid,sp_id,size,mean,var,lb,hb〉判断查询哪些簇的存储节点，然后基站向传感器网络发布查询命令〈qv,k,spid,〉给特定的存储节点，其中查询命令qv表示要查询的数值，spid={sp_id,sp_num}表示将要查询的存储节点的集合，sp_num表示查询在该簇内距离qv最近的sp_num个数据。由于本文的LVC算法考虑了位置信息，因此，两个簇之间的测量范围可能会产生重叠(如图2所示)。

图2 簇的测量范围

若查询数据只存在一个簇内，即lbi≤qv≤hbi，则查询存储节点的数量为1，sp_num=z；若查询数据存在于两个簇内或在两个簇的测量范围之间(hbi≤qv≤lbi+1)，则查询存储节点的数量为2，即sp_num1+sp_num2=z。当查询存储节点的数量为2时，最直接的方式是将两个簇内的所有测量值都传送给基站，然后由基站计算K近邻，但当簇内节点较多或k较小时这将消耗较多的能量，本文提出基于数据离散度的近似KNN 数据查询算法解决sp_numi数量分配问题。根据查询数据在簇内出现的概率估计出每个簇的查询数量，降低传输数据的数量，从而降低网络的能量消耗，该算法伪代码如下：

初始化:sp_num1=0,sp_num2=0,pd1=1,pd2=1P1=12πvar1exp-(qv-mean1)2(2var1) P2=12πvar2exp-(qv-mean2)2(2var2) for i=1:qif ((pd1·P1)>(pd2·P2)) sp_num1=sp_num1+1 pd1=pd1·P1else sp_num2=sp_num2+1 pd2=pd2·P2endend

3 仿真与结果分析

在300m×300m区域内，160个传感器节点随机部署进行仿真实验，传感器节点的通信半径为50m，路由协议采用GPSR[11]协议。

图3给出LVC分簇后的结果，其中簇1和簇2的数据比较接近，但二者地理位置相距较远，由图3可知，LVC算法可以将测量数值相近但地理位置相距较远的节点分类。

图3 LVC算法效果

图4给出三种算法在不同查询率下平均传包率的对比。查询率：当节点向存储节点传送一个数据包时，基站向存储节点发送查询指令的次数。平均传包率=查询一次传送数据包的总个数/节点数量。

图4 平均传包率与查询率的关系

由图4可知，随着查询率的提高，本文提出的CAKNN算法与KVC算法均提高；由于Naïve算法不受查询率的影响，因此，平均传包数不变；但CAKNN算法与KVC算法的平均传包数始终小于Naïve算法。当查询率小于0.7时，CAKNN算法优于KVC算法，其中最大可提高30.36%；当查询率大于0.7时，KVC的算法略优于CAKNN算法。平均传包率越小，系统传送数据包的数量越少，节点消耗能量越少，网络生存时间也就越长。由图4可知本文提出的CAKNN算法具有更低的平均传包率，因此网络的生存时间更长。

4 结论

提出基于位置-数据的分簇方法，该算法首先将测量数据值和地理位置接近的节点分为一簇，降低了网络的能量消耗，然后利用数据的离散度确定查询存储节点数据的个数，解决了簇之间测量范围重叠的问题。仿真结果表明：通过与Naïve算法、KVC算法比较，本文提出的CAKNN算法具有较低的平均传包率，节约了节点的能量，提高了网络的生存时间。