基于N 进制位权下NAF 的椭圆曲线标量乘算法

赵增

（上海海事大学信息工程学院，上海 201306)

0 引言

椭圆曲线密码体制（Elliptic Curve Cryptography，ECC）被Miller[1]和Koblitz[2]分别的独立提出以来，受到密码学科研工作者的广泛关注和高度重视。ECC与其他公开的密码体制对比，它拥有自己的优点，例如运算效率高、安全等级相同时ECC所需密钥长度短、ECC所需的带宽少等。这些优点促使ECC能在安全领域得到广泛应用和研究。在当今信息化，大数据的时代，信息安全关乎重大，如何更迅速使得信息加密与解密也至关重要，因此ECC运算效率的提高也是该领域研究者的研究热点。

在有限域Fq上椭圆曲线上的标量乘（点乘）是实现ECC加解密的关键步骤，这直接影响到ECC的运算效率。有个大的整数k和有限域Fq上椭圆曲线上的一个基点P，所谓的椭圆曲线上的标量乘就是计算kP。为了提高椭圆曲线密码体制的运算效率，可以从有限域Fq上椭圆曲线上的标量乘着手。以前的研究者提出了二进制方法、NAF方法、Montgomery标量乘、Frobenius标量乘和固定基窗口方法等[3-5]。但是以上的算法要么是基于正整数k的分解方式，要么是基于底层域的减少点加与倍点上的求逆次数，这两种方式从而来提高椭圆曲线上点乘的运算效率。没有用这两种方式交互融合，互相促进的方式来提升椭圆曲线上点乘的运算效率。

针对以上问题，本文提出了一种基于N进制位权的非相邻形式的椭圆曲线标量乘的快速算法（简称为NBW-NAF算法）。NBW-NAF算法在实现过程中利用预计算生成预置表，通过查询预置表使得算法的在进行多次点乘运算时效率得到提升。又由本文新提出的N进制位权的非相邻形式的特点，这种编码方式比常规二进制的编码的位数更短，而且结合非相邻形式的特点，极大减少了NBW-NAF算法主要循环步骤中的点加和N倍点的运算次数，从而使得NBW-NAF算法拥有更高的运算效率。

1 相关知识介绍与分析

本节对椭圆曲线上的点群的运算的概念进行介绍，之后对现有的个别方法进行举例分析，提出有待改进的方向。

椭圆曲线上的点群的运算可以概括的分为两层，即底层的点加与倍点运算和上层的点乘运算。

对于底层的点加与倍点运算，由于在不同的特征的有限域Fq上的椭圆曲线的点加与倍点运算有少许差异，篇幅有限，本节只介绍在特征等于2的有限域上的点加与倍点运算的情况。其他情形查考文献[6]。

其中a,b∈F2m，其判别式b≠0，其无穷远点记为∞。对于任意的Q=(x2,y2),P≠±Q其上的点加公式P+Q=(x3,y3)为：

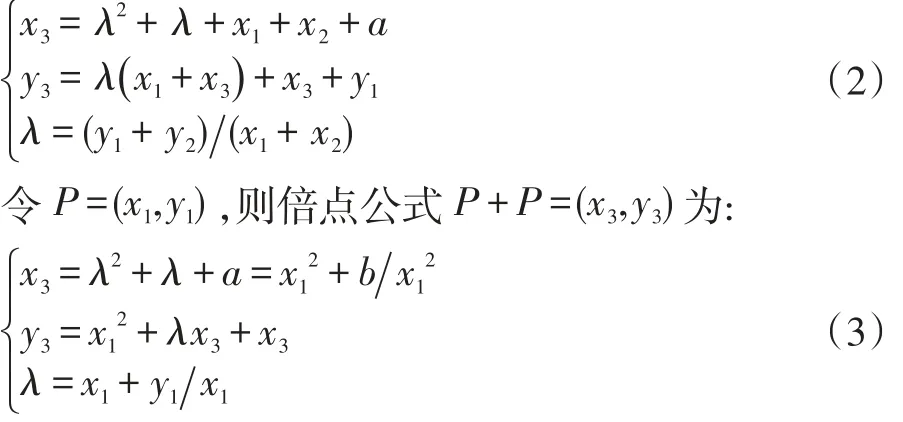
文献[8]在公式（3）的基础上提出直接计算4P，8P，16P的公式。文献[9]在此基础上给出了直接计算2sP，1≤s≤m的公式。令2sP=(xs,ys)，P=(x0,y0)即得公式：其 中 cs= δ2,as=λ2+δλ,bs=as-14+δλxs而 δ=as-1cs-1,λ=as-12+bs-1cs-1,初始值 a0=x0,b0=y0，c0=1。

而文献[10]给出了直接计算3P，5P，3kP，5kP的计算方法。

2 基于N进制位权的非相邻形式的椭圆曲线标量乘的快速算法

2.1 正整数展开成N进制位权的非相邻形式

为了提高椭圆曲线上的计算点乘kP的效率，先把整数k转换成N进制，之后用N进制位权的非相邻形式来表示整数k，即下文中的算法1来实现。

（1）N进制位权的非相邻形式定义及性质

定义1数制中的一个m位整数k，在数k的任意编码位置处都有相应的与其对应的单位权值，我们把这一单位权值称为与其位置对应的位权。

例如，一个8位十六进制编码的整数k，其编码为F1010E01。整数k的第0位处的数值为1，其位置相应的权值为160，此位置处代表的数据为 ，此时把整数k的第0位记成K0，把K0相应的权值称为K0位权。

性质（N进制位权的非相邻形式的性质）令k是一个正整数。

●K一定存在N进制位权的非相邻形式，并记为NBW-NAF(k)。

●NBW-NAF(k)在k的所有带符号形式中具有最少的非零位。

●NBW-NAF(k)的长度最多比k的N进制形式的长度大1。

●NBW-NAF(k)的长度最多比k的N进制形式的长度小1。

定理1对于任意正整数N和已知椭圆曲线上某一基点P，我们一定可以推导出直接进行计算在有限域F2m

上椭圆曲线的点乘NP运算公式。

（2）正整数展开成N进制位权的非相邻形式的构造过程

由N进制位权的非相邻形式的定义，其中没有任意连续相邻的不同位权处的数值是非零的，并且每一位权处的数值不大于■■N22。因此在把正整数k转化为NBW-NAF(k)的算法中有如下的步骤。

首先，利用进制转换把正整数k转换成N进制，即，用k除以N，得到整数商和余数，记录余数，之后，用k减去余数从而整除N得到的整数来更新原来的整数k的值，再用新得到的整数k除以N，得到新一轮的商和余数，如此反复，直到最后k迭代成0为止。即算法1中第2步～第8步中得到的(N_Ki,…,N_K1,N_K0)就是正整数k的N进制表达式。

之后，对正整数k的 N进制表达式(N_Ki,…,N_K1,N_K0)从右到左执行更新分离算法使得任意相邻位权处的非零数不相邻。即算法1中第11步到第18步，每次处理2个位权位置处的数值。

最后，经过前两个步骤之后得到的返回数(Kl-1,…,K1,K0)即为正整数k的N进制位权的非相邻形式。其伪代码如算法1所示。

算法1正整数展开成N进制位权的非相邻形式的算法

输入：输入正整数k，选用k的N进制形式中的N（N＞1）

输出：代表正整数k的 NBW-NAF(k),即表示为：(Kl-1,…,K1,K0)

2.2 基于N进制位权的非相邻形式的椭圆曲线标量乘的快速算法的实现

由于N进制位权的非相邻形式中每一位置处的位权和其相邻处的位权差值不再是2倍关系，所以椭圆曲线密码体制中的倍点公式不能直接用到现在的N进制位权的非相邻形式的椭圆曲线点乘运算中。在特征为2的有限域F2m上的椭圆曲线上的点乘，我们可以有定理1推出直接进行计算NP的公式。在此基础上，我们结合算法1得到的正整数展开成N进制位权的非相邻形式进行展开，从而得到计算有限域F2m的椭圆曲线上的点乘。如下算法2所示。

算法2基于N进制位权的非相邻形式的椭圆曲线标量乘的快速算法

输出：输出椭圆曲线密码体制中点乘的值，即kP

1. 调用正整数展开成N进制位权的非相邻形式的算法，并把输入参数k，N传递给此算法。此算法返回k的NBW-NAF（k），即：(Kl-1,…,K1,K0)

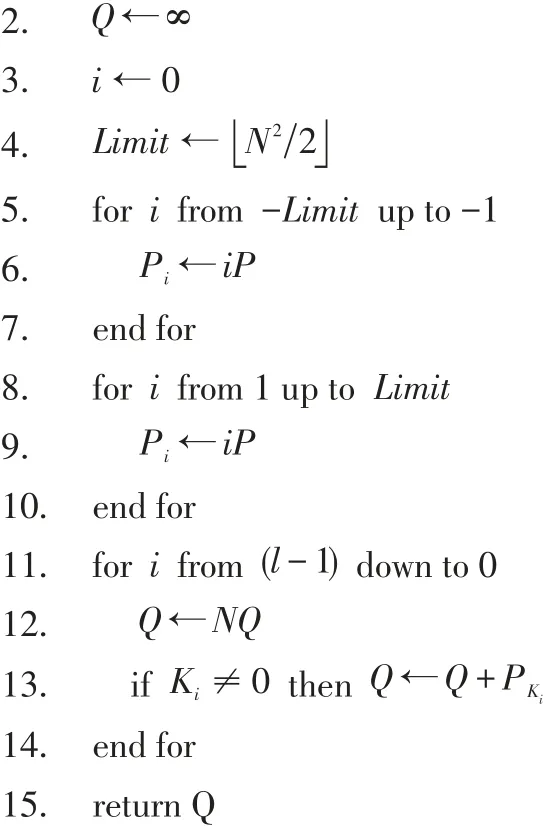
3 算法分析与仿真实验

首先对NBW-NAF算法进行理论证明与分析，然后把NBW-NAF算法与其他相关算法进行对比。为了比较的公平性与合理性，本文对实验中的单位进行了统一的归一化处理。

3.1 NBW-NAF算法的正确性分析

（1）算法的终止

对于算法1的步骤（2）到步骤（8），由于正整数k是有限的，所以算法1可以跳出while循环，由步骤（9）可知m是有限的，所以算法1的步骤（11）到步骤（18）也会执行完，因此算法1也一定会终止。同理算法2也一定会终止。

（2）算法的正确性

算法的正确性证明：

由N进制位权的非相邻形式的性质可得，算法1一定可以把正整数k转化为NBW-NAF(k)。由算法1中第2步～第8步可知(N_Ki,…,NK1,NK0)=k，又由第11步到第18步可知(N_Ki,…,NK1,NK0)=(Kl-1,…,K1,K0)，所以k=(Kl-1,…,K1,K0)=NBW-NAF(k)。在k=(Kl-1,…,K1,K0)=NBW-NAF(k)的基础上，又由定理2和算法2的第11步到第13步可得NBW-NAF算法的椭圆曲线点群上的点乘运算可以表示为：

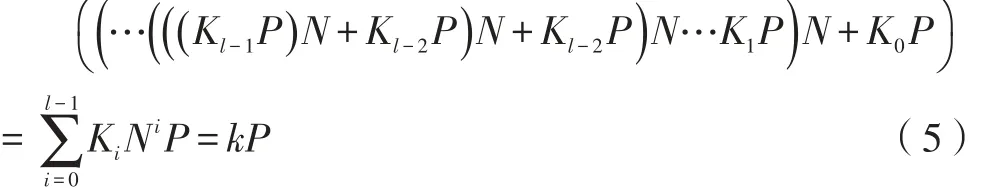
由公式（5）的可得NBW-NAF算法计算点乘kP的运算是正确的。

3.2 仿真实验

为了到达实验的公平性与合理性，采用的是NIST推荐的椭圆曲线[11]定义在有限域F2m，椭圆曲线方程为：y2+xy=x3+ax2+b，基点为P(Px,Py)，其中阶数为n，该椭圆曲线的参数设置见表1。以0x开头的数据代表16进制数据。

表1 椭圆曲线参数设置表

为了进行合理公平的比较，我们为其选择了共同的实验环境，其设置2.6GHz的i7处理器，8GB的内存空间。我们选择的编程工具是Visual Studio 2015，编程语言是C++。随机生成6组256位随机正整数。然后用这6组正整数与基为P(Px,Py)做点乘。下表2列出不同算法件的对比结果。由表2得NBW-NAF算法在N=2的情况下与二进制NAF算法的效率相当，在N＞2效率提高了26.91%～31.72%。

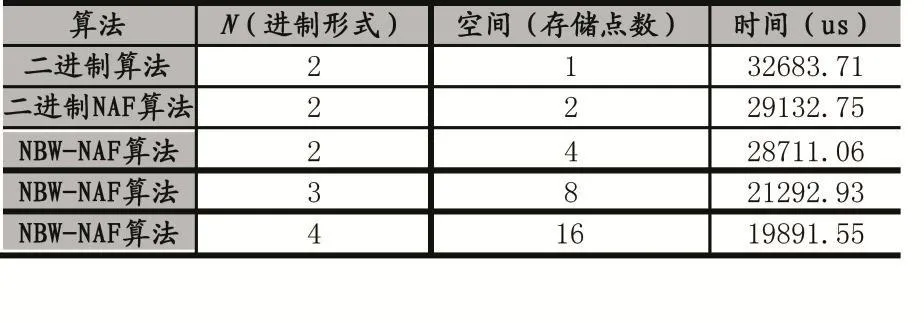
表2 不同算法点乘运算比较表

4 结语

本文提出了一种基于N进制位权下非相邻形式的椭圆曲线标量乘算法：NBW-NAF算法。该算法结合了N进制位权下非相邻形式下的优势与多进制下算法移位操作需要多倍点运算的优势，使得整体运算中求逆的次数大大减少，又通过查询预置表，从而有效减少了运算过程中的时间开销。本文对NBW-NAF算法的可行性、正确性分析证明以及效率分析验证进行了详细的描述。仿真实验表明，与其他同类算法对比,NBW-NAF算法具有更高的运算效率。