基于BOTDA 布里渊增益谱拟合的去噪算法研究
2018-08-01徐飞耀安博文陈元林
徐飞耀,安博文,陈元林
(上海海事大学信息工程学院,上海 201306)
0 引言
BOTDA(Brilouin Optical Time-Domain Analysis),即布里渊光时域分析技术,是一种基于受激布里渊背向散射的分布式光纤传感技术。该技术根据光纤中背向布里渊散射光的频率偏移量与光纤应力和温度的变化呈良好的线性关系这一原理,可以同时测量得到光纤路径上被测量范围内连续的应力和温度信息,具有测量精度高、传输距离长、测量范围大,抗电磁干扰、耐腐蚀等诸多优点。该技术在桥梁、隧道、管道及大型结构物等健康状况的监测领域具有广阔的应用前景[1]。
在分布式光纤传感系统中,由于光纤放置环境复杂多变,其周围的温度、湿度、应力等各种因素,以及在信号传输转化过程中系统自身所引起的噪声,使得待检测的信号在中远距离传输情况下被噪声严重干扰[2]。空间分辨率、测量精度、测量实时性和传输距离是分布式光纤传感系统的重要性能指标[3],作为具备高测量精度和高分辨率的传感设备,如何准确快速提取布里渊增益谱的关键信息即布里渊中心频率成为提高BOTDA测量精度的关键之一。目前,获得布里渊中心频率的方法主要是对布里渊增益谱的二维离散数据进行曲线拟合,由波峰位置确定中心频率,国内外学者在这一问题上进行了深入研究并提出多种优化算法。文献[4]分析了入射脉冲宽度远小于10ns(光子寿命)情况下背向布里渊增益谱,通过实验数据对比提出了更加准确的洛伦兹-高斯线性权重优化组合的Pseudo-Voigt模型;文献[5]提出了无需经过曲线拟合快速方便的互相关学习法、深度学习法和亚像素级精度的重心提取算法,具备更大的扫频范围和良好的实时性;文献[6]利用定积分法改正了半峰宽的初值选取方法,提高了单峰背向布里渊散射谱的拟合精度。上述方法在实验模型和曲线拟合方法上进行了改进,忽略了噪声对于实验结果的影响。文献[7]在使用小波变换方法没有考虑实时性对于系统的重要性。本文将基于真实BOTDA设备数据对背向布里渊增益谱进行研究,通过提取不同长度光纤尾端位置的背向布里渊散射数据的噪声及对噪声功率谱进行分析,提取出噪声特征并对原始数据进行针对性去噪处理,提高了中远距离情况下布里渊增益谱的准确性和实时性。
1 BOTDA工作原理及模型选取
光在光纤中传播时大部分光是向前传播的,但由于光纤材料的光学性质(如密度、材料组成、温度、应力等)存在微观不均匀性,入射光束的一小部分光在原来的传播方向产生散射现象,主要包括瑞利散射、布里渊散射和拉曼散射,如图1所示。由于同时对温度和应力具备更高的敏感性和测量距离长等优点,布里渊散射更受关注。
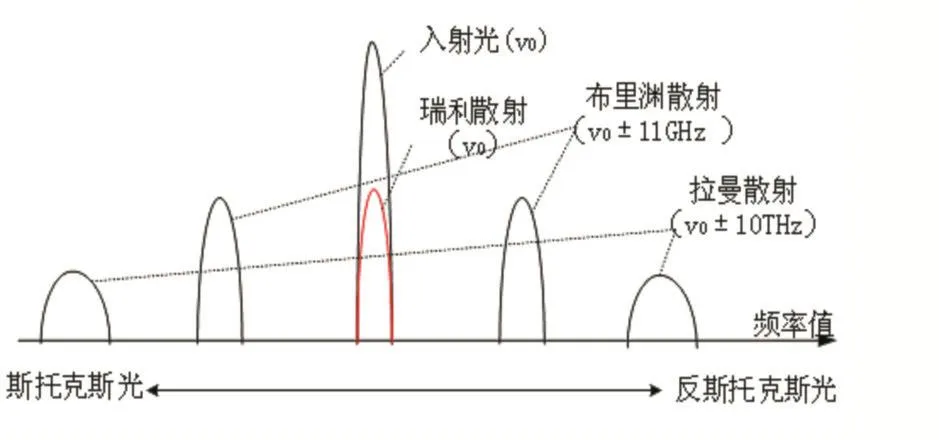
图1 光纤中主要的三种散射形式
BOTDA是通过分析光纤中受激布里渊背向散射光的频率偏移量来计算光纤路径上各点的应力和温度信息。布里渊散射同时受应变和温度的影响,当光纤沿线的温度发生变化或者存在轴向应变时,光纤中的背向布里渊散射光的频率将发生偏移,频率的偏移量与光纤应变和温度的变化呈良好的线性关系:

其中ΔVB为布里渊光频移变化量,Δε为传感光纤(离入射端面距离)处的应变变化,ΔTR为传感光纤处的温度变化,Cε和CT分别为光纤的布里渊散射频移应变系数和温度系数。
由上述公式可知,获取布里渊散射频移量,即可计算出对应的应变或者温度信息。布里渊散射频移量的获取原理如图2所示。
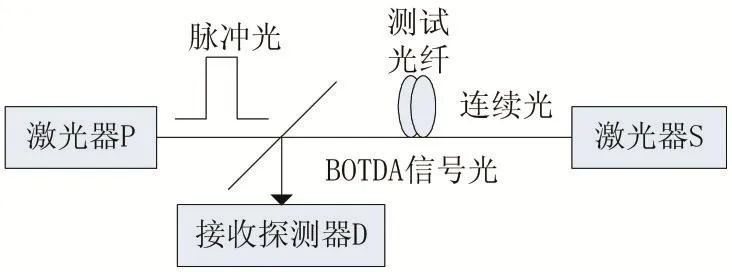
图2 BOTDA工作原理框图
接收探测器D接收的背向散射光能量与脉冲光和连续光的频差有关,当泵浦光和探测光的频差同光纤中某区域的布里渊频移相等时,在该区域就会产生布里渊放大效应(受激布里渊散射,Stimulated Brillouin Scattering,SBS),此时探测能量值最大,对应的频差称为布里渊中心频率。系统通过扫频方法获取中心频率,定义脉冲光与连续光的频差范围[f1,f2]为扫频范围,以步长Δf在[f1,f2]区间内依次改变脉冲光和连续光频差进行探测,探测器D可接收到对应能量值,如图3所示,横坐标为频差,纵坐标为频差对应的功率值。
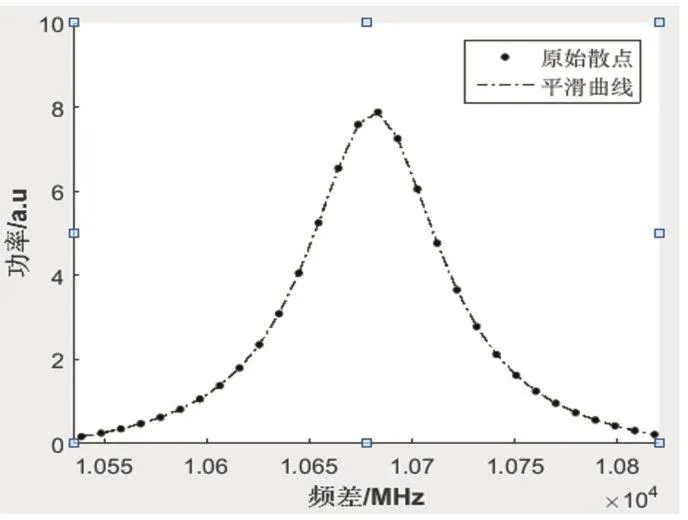
图3 布里渊增益谱功率扫频图
利用检测系统检测从光纤一端耦合出来的连续光功率,及通过对背向布里渊增益谱的离散数据进行曲线拟合得到的对应光谱的波峰位置,即可得到光纤中对应位置能量转移达到最大时的布里渊频移量,然后根据布里渊频移与应力温度的对应关系,即可得到应力、温度数据,从而实现光纤数据的分布式测量。
理论上,布里渊增益谱为洛伦兹(Lorentzian)型曲线,如图4所示。
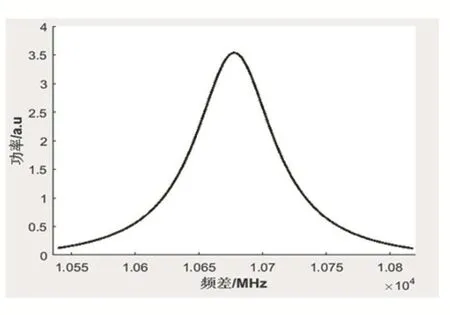
图4 洛伦兹(Lorentzian)型曲线
布里渊增益谱光功率的洛伦兹函数数学表达式为:

2 研究方案概述
本文技术路线如图5所示。首先对布里渊增益谱数据进行采集,分析采集到的原始数据并对其参数进行评估。通过参数确定噪声存在对于数据的影响,将噪声从数据中分离并对其做功率谱分析,根据信号和噪声功率谱分布确定去噪方法进行数据处理,最后对不同方法处理数据的效果进行对比,得出结论。
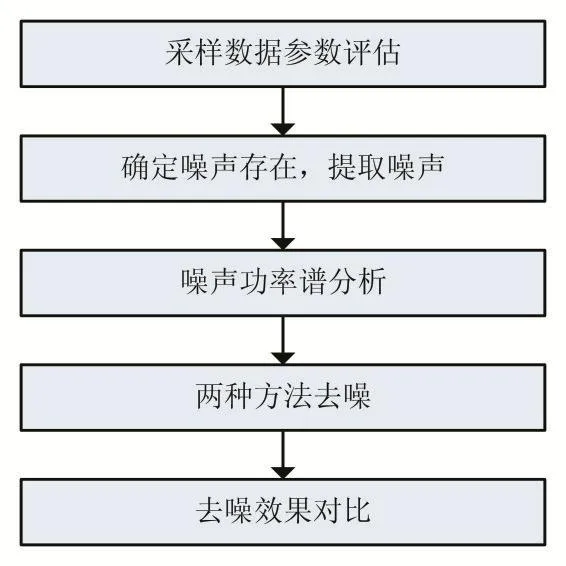
图5 噪声处理流程图
3 研究过程及关键技术
3.1 实验条件及数据采集
实验目标是采集不同长度光纤尾端位置的布里渊增益谱信号。实验中采样步长0.32m、脉冲宽度10ns、频差范围为10530MHz-10800MHz、扫频间隔10MHz。实验光纤在12.7摄氏度室温情况下的布里渊中心频率为10676.15MHz,每次采样数据为连续扫频8000次的平均值。
在上述参数条件下进行数据采集、方法设计、结果分析和讨论。
对于最小二乘法的非线性曲线拟合,高斯-牛顿迭代法具备更好的全局搜索、判断能力和更高的收敛速度。本文使用传统方法对上式中的参数进行取初值,设置迭代次数为30,当到达迭代次数后停止计算,此时结果作为输出。
BOTDA系统中有很多噪声来源且很难被消除,包括光源噪声、光传输噪声和光电接收噪声。随机均匀噪声可以通过多次叠加平均的方式进行去除,该结论已被多次验证,所以本文将重点放在叠加平均无法去除的非均匀噪声上,所有原始数据均已通过叠加平均去噪。
在实验前期,通过BOTDA设备采集光纤长度分别为1km、3km、5km和10km的尾端数据,在不同长度光纤情况下固定点连续采集20组数据(记为i)、每组采集数据包括30个频差点的布里渊散射数据(记为 j),其中第15个频差点的位置接近布里渊中心频率。四种 长 度 光 纤 原 始 数 据 分 别 记 为 Aij、Bij、Cij、Dij(1≤i≤20,1≤j≤30)。
3.2 原始数据离散度分析
首先,使用MATLAB工具对四种不同长度光纤的布里渊增益谱数据进行归一化处理,计算原始采样数据方差,结果如图6:
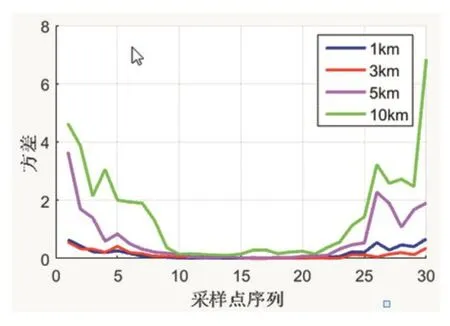
图6 布里渊增益谱原始数据方差
由图6可以看出,随着光纤长度的增加,布里渊频谱数据的离散程度随之增大,且相同长度光纤布里渊增益谱数据的离散程度由布里渊中心处向两边增大。
使用高斯-牛顿迭代法对采集的布里渊增益谱离散数据进行拟合。曲线拟合得到的布里渊中心频率及其方差如图7和图8所示:
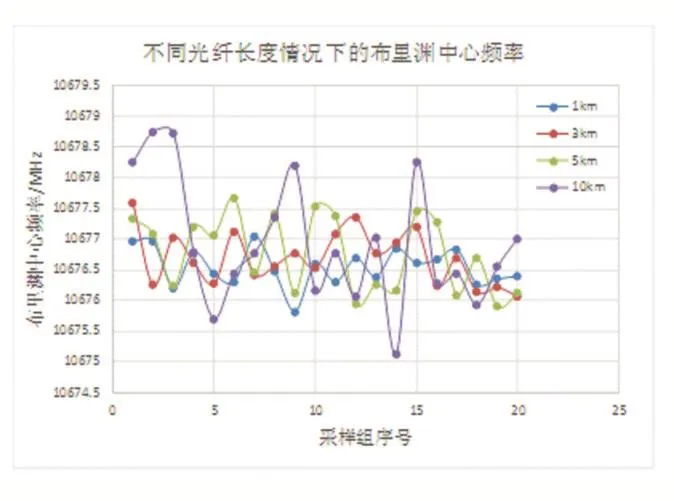
图7 布里渊中心频率
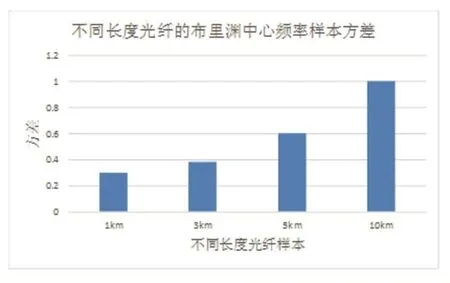
图8 不同长度光纤布里渊中心频率方差
由图7和图8数据可以看出,随着光纤距离的增加,布里渊增益谱中心频率数据的离散程度增大、准确度下降,说明噪声存在并对数据造成严重影响,准确提取布里渊增益谱的特征变得十分困难。有效去除噪声才是提高长距离情况下布里渊增益谱准确性的关键。
3.3 噪声提取
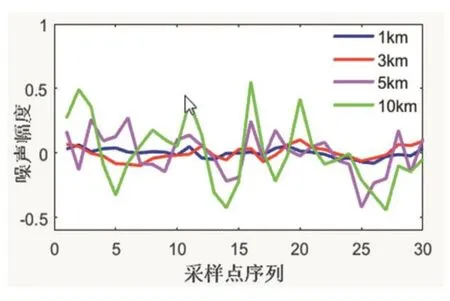
图9 布里渊增益谱噪声
3.4 噪声功率谱分析
对不同长度光纤的原始数据和噪声数据分别进行AR功率谱估计,展示信号功率随频率的变化情况。根据本文布里渊中心频率所处的位置位于采样点i=15左右,对该处数据做AR功率谱分析,结果如10所示。
从图10中通过对比可以看出,在对原始数据进行多次叠加平均去除白噪声后,不同长度光纤的信号功率谱能量主要集中在低频段,噪声数据的功率谱较为平稳,在400Hz以上的高频段信号数据功率谱和噪声数据功率谱几乎重合,所以,应该对含有大量噪声的高频段原始数据进行滤波去噪。
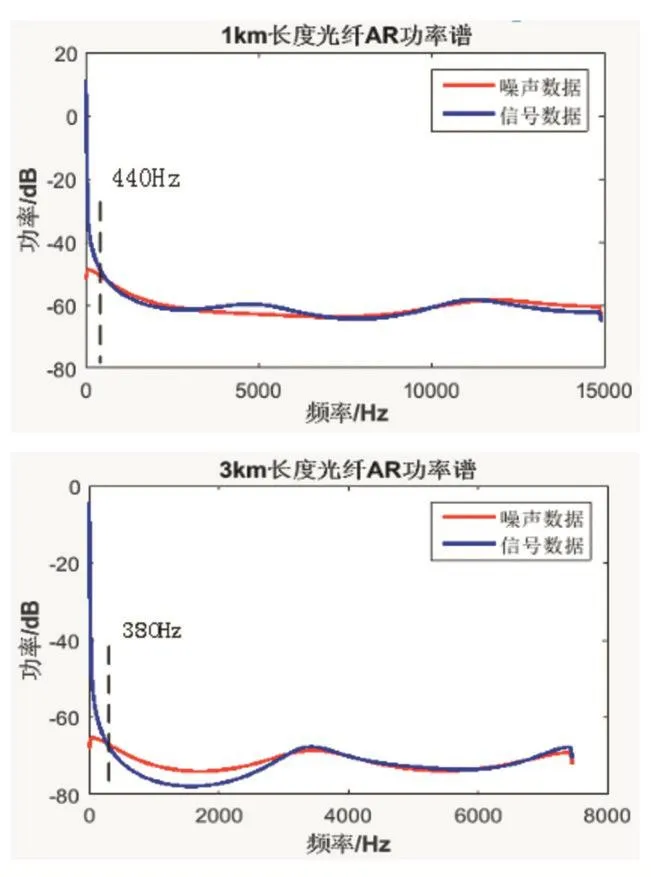
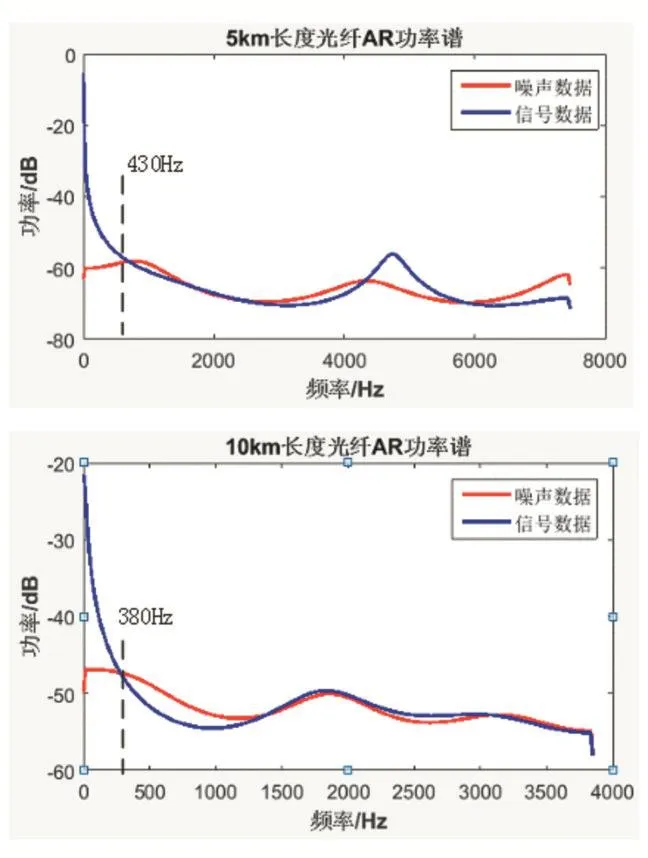
图10 不同长度光纤AR功率谱
3.5 不同去噪方法
(1)低通滤波器去噪
滤波是将信号中特定波段的频率滤除的操作,是抑制和防止干扰的一项重要措施,其基本原理是根据变换域频谱特征对信号中频率成分选择的过程。由于巴特沃斯(Butterworth)滤波器在同频带的频率响应曲线最为平滑,结合本文信号和噪声频谱特征,选择巴特沃斯低通滤波器进行信号去噪处理。
(2)小波去噪基本原理
小波变换的基本思想是用2个或2个以上的函数(小波基)去逼近原函数[8]。由于信号中有用部分和噪声具有不同的时域特性,因此,通过选取合理的阈值可以有效去除噪声信号[9]。
小波去噪主要分为以下三个步骤[10]:
①选择合适的小波基和分解层数,计算各层小波分解的系数;
②针对每一分解层次选择一个阈值,对高频系数进行处理,去除集中在高频部分的噪声成分;
③针对每一分解层次,对低频系数和阈值量化处理后的高频系数进行小波重构,获得去噪后的信号。
流程图如下[11]:
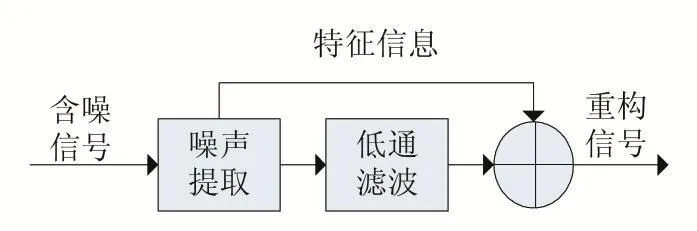
图11 小波信号去噪过程图
小波去噪方法主要分为三类:模极大值重构滤波、空域相关滤波和小波阈值滤波[12]。由于信号在空间上表现出一定连续性,因此在小波域有效信号所产生的小波系数其模值往往较大;而噪声在空间上没有连续性,经过小波变换后在小波域表现出很强的随机性,因此选择合理的阈值就能很大程度上抑制噪声而降低对有效信号的伤害。根据信号特征对阈值进行对应改变的软阈值函数因使得小波系数整体连续性较好、不会产生附加震荡、信号更加平滑等优点得到广泛应用。
4 去噪算法效果对比
4.1 方法一:低通滤波器法
根据图10对数据进行AR估计得到的功率谱,对于长度为1km、3km、5km和10km的光纤,分别选择440Hz、380Hz、430Hz和 380Hz作为低通滤波器的截止频率,对数据进行滤波处理。
首先,将原始数据进行滤波处理,通过对应截止频率的低通滤波器,如图12所示。
从图12可以看出,滤波之后的布里渊增益谱曲线更加平滑,噪声减少。其布里渊增益谱中心频率和方差如表1、2所示。
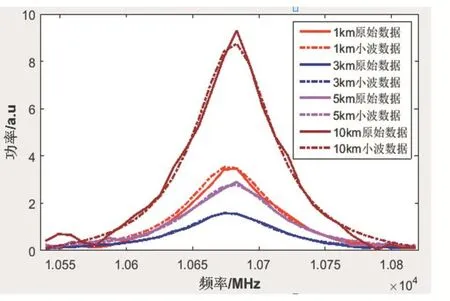
图12 滤波器去噪前后布里渊增益谱
4.2 方法二:小波变换去噪法
对于小波变换去噪方法的效果,进行以下验证实验。本文以布里渊中心频率准确度和方差作为去噪效果衡量的指标。通过实验测试,选择效果最好的“db4”小波基、分层数为3层,实验所得数据如图13所示,统计结果如表1、2所示。
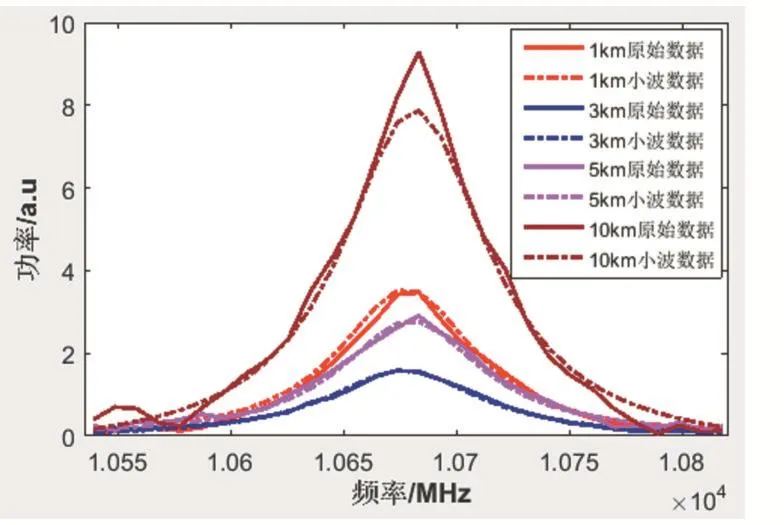
图13 小波去噪前后布里渊增益谱
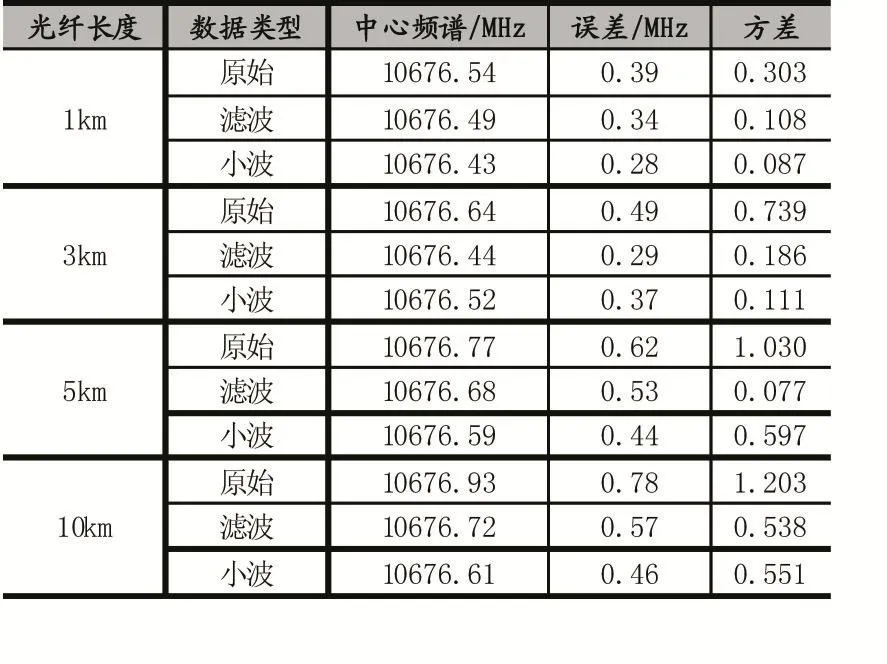
表1 不同去噪方法效果对比

表2 不同方法耗时比较
从上面表格中数据可以看出,在布里渊中心频率计算误差和方差方面,滤波方法和小波变换都具备良好的滤波效果,数据误差和方差得到改善,方差改善尤为明显,使得布里渊中心频率的准确性得到大幅提升。但在单点滤波耗时方面,低通滤波器方法耗时明显低于小波变换,仅是后者的1/26,对于中远距离光纤监测在实时性方面具有十分明显的优势。
5 结语
随着传感光纤长度的增加采样信号中的噪声也随之增加,进而影响BOTDA布里渊中心频率的准确性,限制其能力及应用。经上述研究分析可以看出,中短距离传感光纤中包括均匀噪声和非均匀噪声,均匀噪声可以通过叠加平均的方式去除,对于非均匀噪声的去除,本文使用低通滤波器滤波和小波变换两种方法进行对比,实验结果表明,两种方法对于BOTDA系统噪声的去除具有良好的效果,尤其数据方差得到明显提升。然而,巴特沃斯低通滤波器在实时性方面表现更加优秀,在监测中远距离光纤系统情况下具备明显优势。该结论可以为中远距离光纤监测系统中BOTDA有效性和实时性的提高问题提供参考。
