间隙单元在独立舱式液货船强度计算中的应用
2018-07-30赵文斌
叶 旭 赵文斌 江 淼
(上海船舶研究设计院,上海 201203)
0 前言
独立舱式液货船是一类特殊类型的船舶,独立舱与主船体之间采用支撑垫块进行连接,支撑结构只能承受垂向压力,不承受垂向拉力。中国船级社上海规范所在 《独立液货舱沥青船结构审图原则》(初稿)[1]中建议用杆单元来模拟支撑垫块,通过在计算中逐步删除出现拉应力杆单元方法进行手动迭代分析,从而得到最终结果。张廷辉[2]等采用杆单元模拟的方法对某一沥青船进行有限元分析。这些可以看出,传统的分析方法都是采用杆单元来模拟垂向垫块,虽做法原理简单,但过程复杂,需要分析人员干预较多,随着工况种类的增加,工作量也成几何级增加,并且容易出错。
间隙单元(GAP)具有只受压不受拉的特性,与垂向支撑垫块的受力特点一致,因此选用GAP来模拟支撑结构,采用非线性计算的方式进行分析。本文采用了NASTRAN中的GAP单元,借助通用的PATRAN前处理软件来完成非线性设置,适用于比较复杂的工况。为了说明GAP单元的正确性,同时用杆单元来模拟垂向垫块,并将两者的结果进行了对比。
1 计算分析
1.1 计算模型
选取某型独立舱式沥青船进行分析计算,模型如图1所示。垂向支撑垫块分布如图2所示(共170块),垂向垫块在横向强框架上分布如图3所示。
1.2 边界条件
边界条件按照中国船级社上海规范所《独立液货舱沥青船结构审图原则》(初稿),如表1所示。

图1 沥青船舱段模型

图2 垂向垫块分布
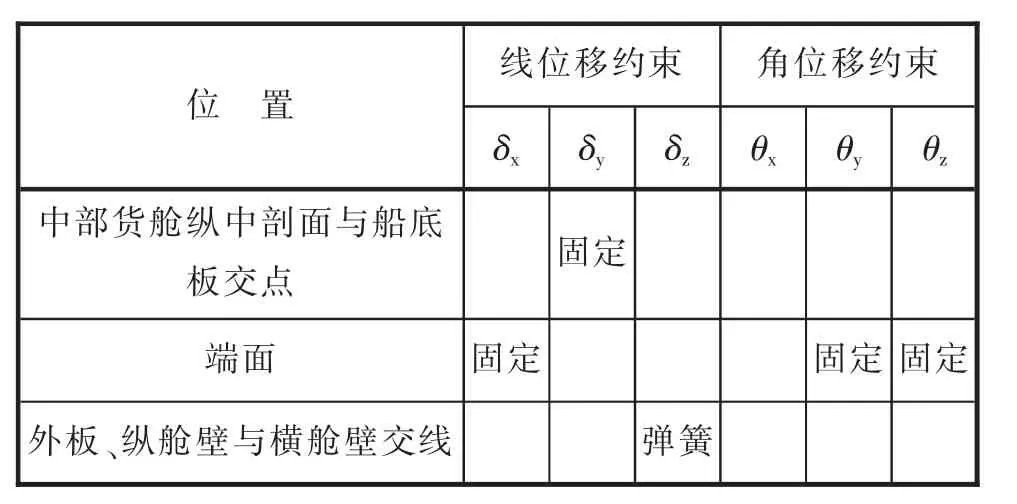
表1 边界条件

图3 典型横向强框架垂向垫块分布
1.3 计算工况
根据中国船级社上海规范所《独立液货舱沥青船结构审图原则》(初稿),选择某一计算工况,如表2所示。
1.4 计算结果
采用一维GAP单元模拟计算,垂向垫块支反力分布如图4所示,数值为0表示垫块不承受垂向压力,图5为实际承受垂向压力的垫块分布。图4和图5 中黑色和灰色分别表示垂向支撑块A和B。
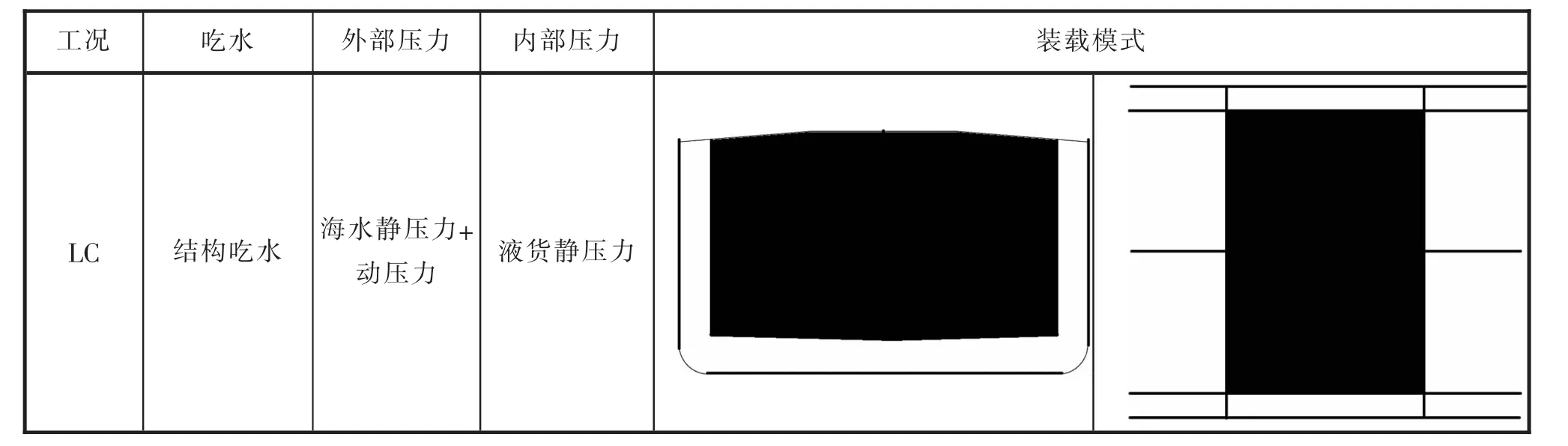
表2 计算工况
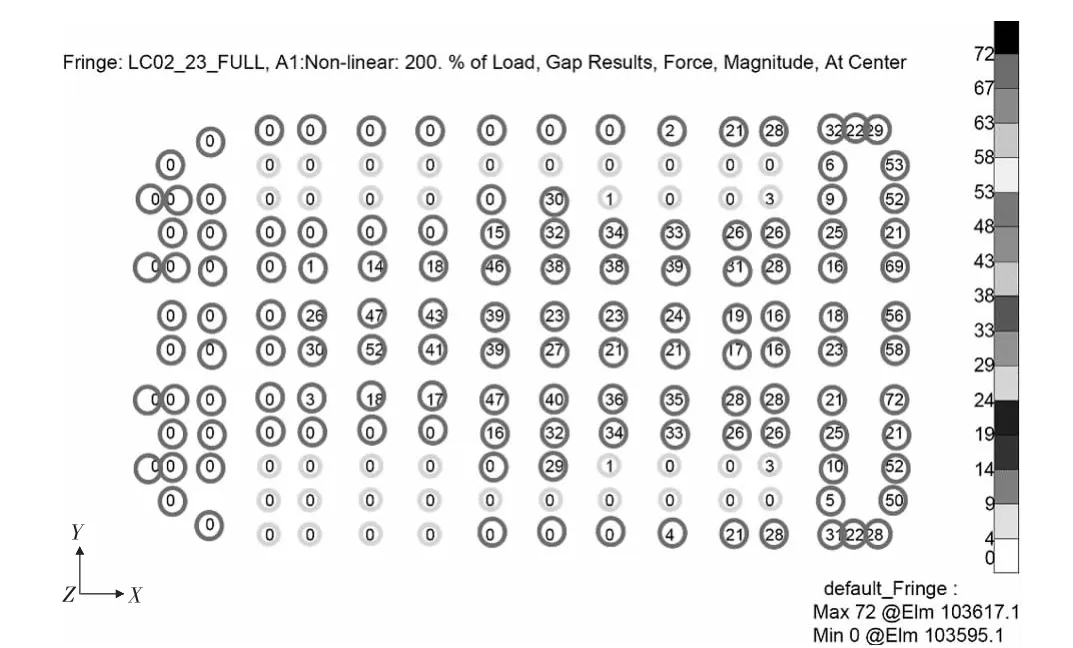
图4 所有垂向垫块支反力分布(单位:10 000 N)
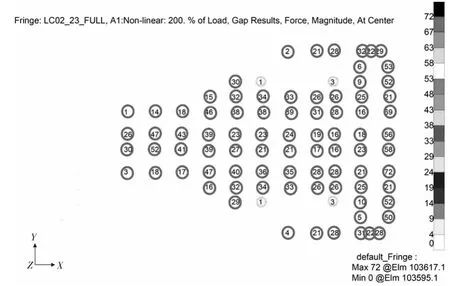
图5 实际承受垂向压力的垫块支反力分布(单位:10 000 N)
从图5中可以看出,实际只有约一半(88/170)的垂向垫块承受压力,其他垫块在结构变形后与独立舱脱离接触。
1.5 杆单元
为了验证GAP单元计算的准确性,采用《独立液货舱沥青船结构审图原则》(初稿)上推荐的杆单元来模拟垂向垫块,杆单元抗压刚度和GAP单元一致,计算工况同1.3。初始杆单元布置和图2一致,如图6表示(大圆圈表示垫块类型A,小圆圈表示垫块类型B)。先进行第1次计算,逐个判断杆单元的相对变形,将受压的杆单元保留,删除受拉的单元,最后保留的垂向垫块数量为146块,如图7所示,即第1次计算有24个受拉的杆单元被删除。
重复上述计算过程,经过8次计算后,所有的垂向垫块均为受压状态,计算完成,最终保留的垫块数量为88,如图8所示。
从图5和图8可以看出,通过GAP单元得到的计算结果和杆单元的计算结果完全一致,这验证了GAP单元模拟垂向垫块的可行性和准确性。

图6 原始分布垫块

图7 第1次计算保留垫块

图8 第8次计算保留垫块
由于杆单元不能直接得到支反力,以图8的bar 1和bar 2为例计算杆单元支反力大小。
首先读取杆单元计算结果的变形值,bar 1的上下两个节点的垂向变形值为28.578 04 mm和28.699 42 mm,bar 2的上下两个节点的垂向变形值为28.881 53 mm和29.012 54 mm。杆单元的刚度为4 300 000 N/mm。支反力大小分别为:
bar 1:
4 300 000×(28.699 42-28.578 04)=520 000 N
bar 2:
4 300 000×(29.012 54-28.881 53)=560 000 N
计算结果和图5中GAP单元的支反力大小一致。
2 GAP刚度研究
使用GAP单元模拟垂向垫块需要计算垫块的抗压刚度,下面研究不同的抗压刚度对计算结果的影响。以上文1.3的例子进行计算,原始的垫块抗压刚度如表3中A0和B0所示。计算4种方案,方案1将GAP单元的刚度整体提高到原始方案的100倍,方案2将GAP单元的刚度整体提高到原始方案的10倍,方案3将GAP单元的刚度整体降低到原始方案的1/10,方案4将GAP单元的刚度整体降低到原始方案的1/100,将4个方案计算得到的垂向垫块支反力和原始方案进行比较,结果如图9~图12所示。
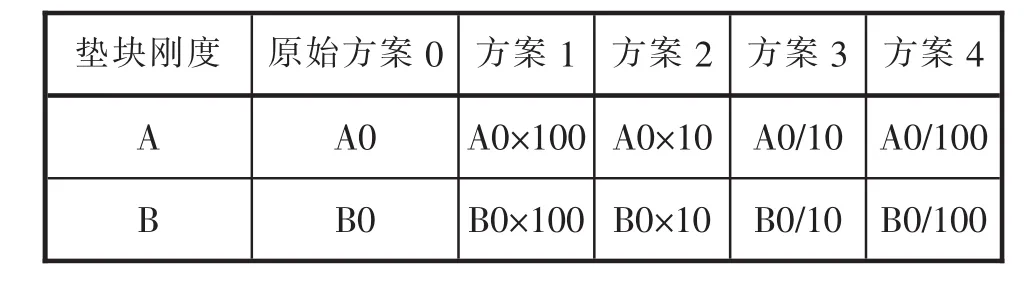
表3 计算方案

图9 方案1和原始方案0垂向垫块支反力差值(单位:10 000 N)

图10 方案2和原始方案0垂向垫块支反力差值(单位:10 000 N)

图11 方案3和原始方案0垂向垫块支反力差值(单位:10 000 N)

图12 方案4和原始方案0垂向垫块支反力差值(单位:10 000 N)
从图9和图10可以看出,GAP单元的整体刚度提高到原先的100倍或10倍时,垫块的支反力和原始方案相比差别很小,只有个别区域出现了差异,可以认为刚度提高对结果不产生影响。从图11和图12中可以看出,GAP单元的刚度下降得越多,支反力的差别越大,差别最大有原先的一半以上。经分析,垂向垫块相对于主船体或独立舱而言,可以看成一个比较刚性的构件,主要用来传递垂向载荷,本身变形可以忽略,GAP单元的刚度整体提高只是将垂向垫块的相对刚度增大,传递的载荷大小基本不变,所以计算得到的支反力没有什么差别。当GAP单元的刚度整体刚度降低10倍或100倍时,垫块已经不能被看成是一个刚性连接结构,GAP本身所产生的变形就会影响独立舱和主船体结构的刚度分布。从图13可看出,当GAP的刚度降低到原始方案的1/100时,各个垫块处的支反力分布得更加均匀,图纸框线区域的支反力从最大72(单位:10 000 N)降低到38(单位:10 000 N)。可以预测,当GAP单元的刚度减小得更多时,垂向垫块的支反力将会更加均匀。

图13 方案4的垂向垫块支反力(单位:10 000 N)
由此,可以得出结论:垂向垫块的刚度整体提高对支撑垫块的支反力影响很小;垂向垫块的刚度整体降低时,支撑垫块的支反力差异较大,结果是不正确的。计算中最好能够准确估算出垫块的抗压刚度。如果实在无法正确估算出刚度值,可以给出一个相对较大的值,计算出的结果是相对可靠的。
3 结语
使用GAP单元模拟独立舱式液货船上的垂向垫块,迭代过程由软件自动完成,保证了计算的准确性。采用杆单元模拟垂向垫块,需要手动删除受拉的杆单元,逐步迭代直至收敛,计算效率低下,计算的准确性需要分析人员严格把控,完成难度较大,不同的计算工况下垂向支撑块的受力分布也不同,每更换一次工况,需要从头开始进行分析迭代。为了追求经济性,垫块的布置都需优化设计,这需要大量的计算,使用杆单元模拟垂向垫块几乎是不可能的。
垂向垫块的抗压刚度对计算结果是有影响的,使用GAP模拟时最好能够提供一个正确的刚度值,或者设计者提供一个相对较大的值,这样对计算结果影响较小。
GAP单元也有自身的不足:它只考虑垂向刚度,忽略了垫块与独立舱的摩擦作用,故设计者需要在后期单独予以考虑。
