关于“你发现了什么”问题的思考

重庆市人和街小学（400015） 刘绪毅

《义务教育数学课程标准（2011年版）》指出：“数学教材为学生的数学学习活动提供学习的主题、基本线索和知识结构，是实现数学课程目标、实施数学教学的重要资源。”人教版教材在中年级的内容中设置了相当一部分的“你发现了什么”的习题，目的是让学生在探究过程中发现规律，领悟数学思想，从而有效积累数学活动经验。怎样将“你发现了什么”的教学目的落到实处，是每一位教师都要思考的问题。

一、梳理分析，理清思路

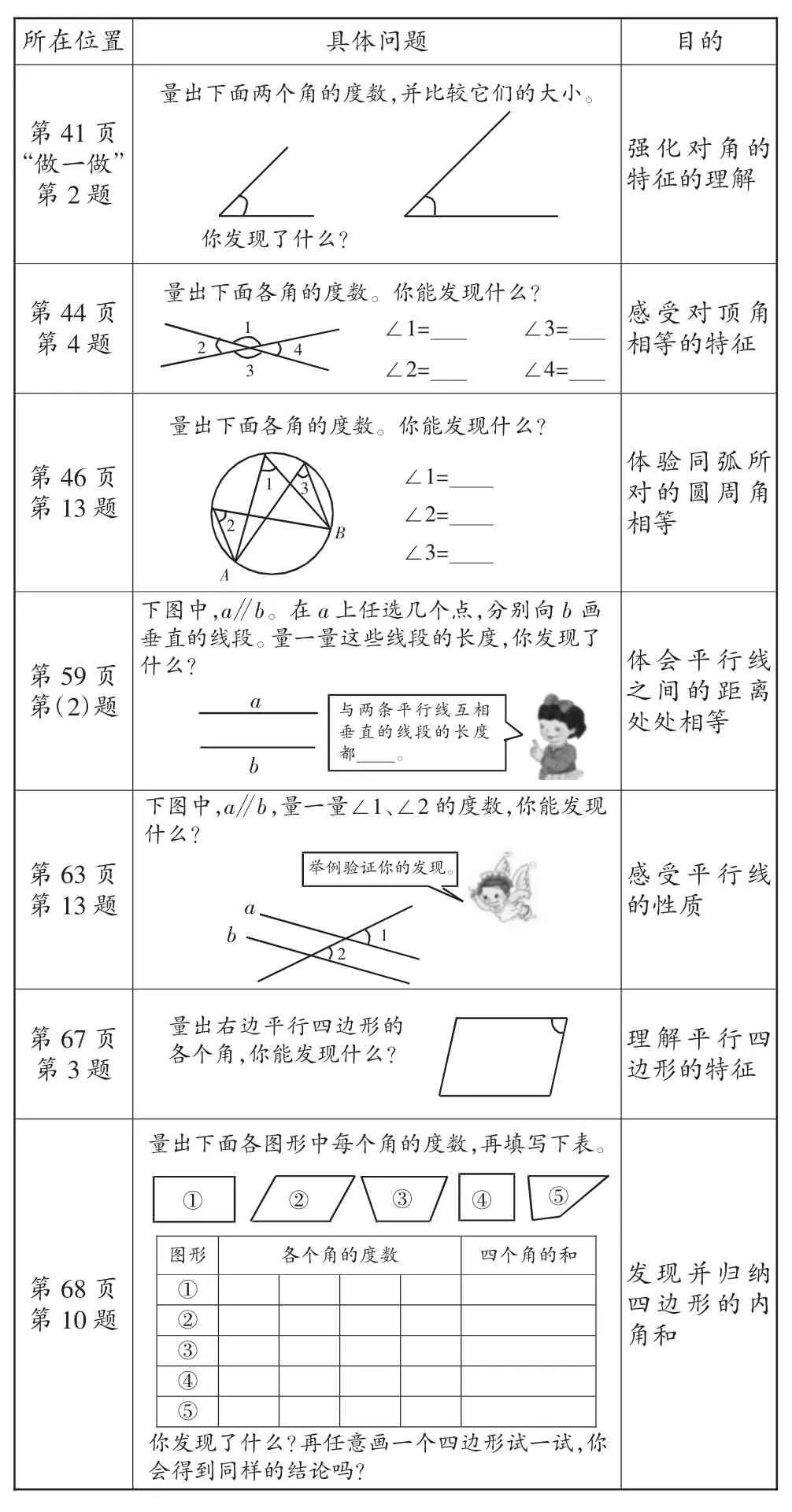
人教版教材四年级上册“你发现了什么”的习题分析表

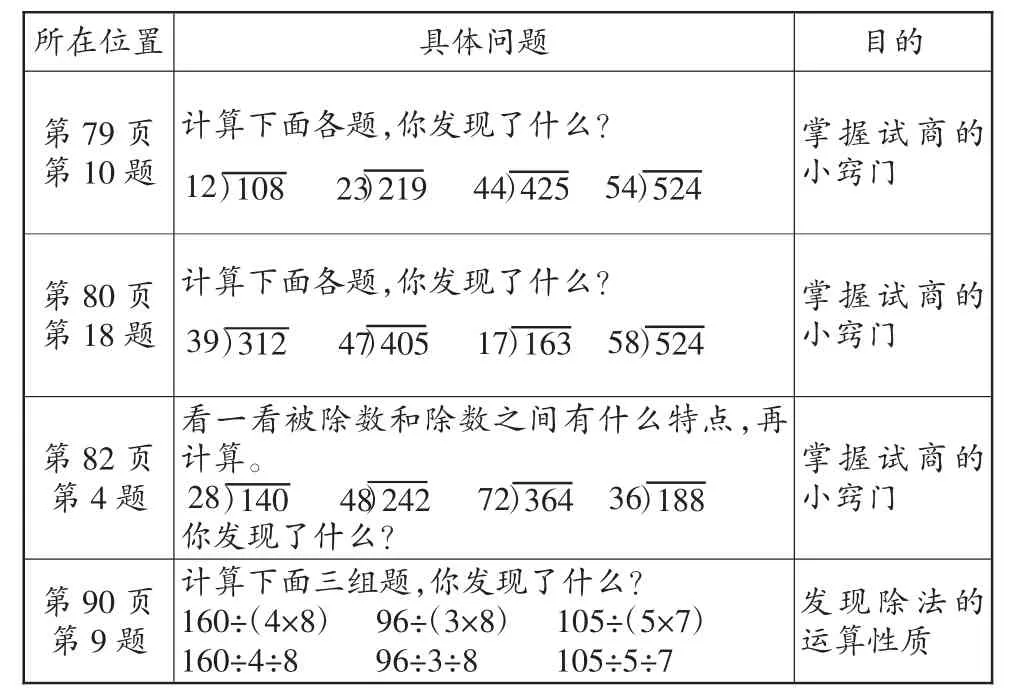
（续上表）

从上表可以看出，“你发现了什么”的习题的编排特点：编者十分重视这类问题，所以数量非常多，但主要集中在“图形与几何”和“数与代数”领域，要求教师不但要让学生经历规律的探究过程，使学生通过操作、思考和交流获得经验，感悟数学思想，发展抽象思维，培养推理能力，还要通过探究的过程，培养学生学习数学的信心，激发学生探究数学的热情，激励学生的创造精神，发展学生的数学素养。

二、理解本质，经历过程

如何帮助学生经历探究的过程？以人教版教材四年级上册第68页的第10题为例进行具体论述。

1.创设情境，激起学生探究的欲望

师：你能根据四边形的特征给下面的四边形分类吗？

生1：可以分为五类。长方形、正方形、平行四边形、梯形和不规则四边形。

生2：我认为可以分为三类。平行四边形（包括长方形和正方形）、梯形和不规则四边形。

生3：我同意生2的看法，因为长方形和正方形都是特殊的平行四边形，他的分类更简洁。

师：你们知道图①和图④的四个内角的和分别是多少吗？

生（齐）：长方形和正方形的四个内角的和都是360度，因为每个角都是90度。

师：你们真聪明！那图②、③、⑤的四个内角和是多少？

生4：可能都是360度。

2.聚焦疑点，引导学生探究

师：怎样验证猜测是否正确呢？

生5：用量角器测量，然后把量得的度数加起来，就能知道猜测正确与否。

师：那就请动手测量这五个图形各个角的度数，并将测量的结果填在下表中。

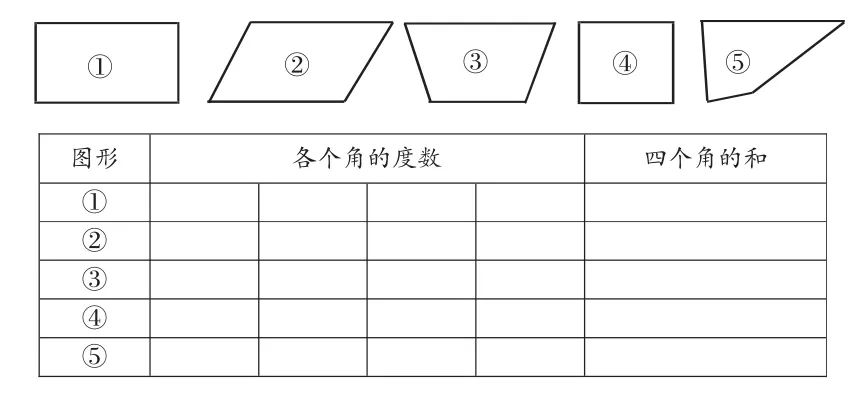
①②③④ ⑤图形 各个角的度数 四个角的和①②③④⑤

3.达成共识，引导学生验证

师：填完表后你有什么发现？

生6：无论是长方形、正方形，还是平行四边形、梯形，它们的四个内角的和都是360度。

生7：这五个四边形的内角和都是360度。

师：通过测量得出这五个四边形的内角和都是360度。现在请大家再任意画一个四边形，看看能得到同样的结论吗？

师：通过测量、计算、填表，你发现了什么？

生（齐）：任意四边形的内角和都是360度。

4．回顾反思，培养学生的反思意识

师：回顾今天的探究过程，你有什么收获？

生8：通过从特殊到一般的方法初步归纳出四边形的内角和为360度，然后通过验证，证明四边形的内角和确实是360度。

生9：通过今天的学习，我学会了用这样的方法去探究其他的数学知识。

师：数学真的很奇妙，数学知识就在我们的身边，只要大家有一双慧眼，就能发现很多数学规律。大家也可以用同样的方法去探究三角形、五边形、六边形等图形的内角和。只要善于思考，善于总结，就能发现很多数学规律。

学生通过测量、计算、填表，逐步发现并归纳出“四边形的内角和是360度”这一规律，体验了从特殊到一般的思维方法，发展了自身的合情推理能力。波利亚认为，学习任何知识的最佳途径是由自己去发现，因为这种发现所形成的理解最深刻，所掌握的规律、性质和联系也最牢固。因此，在教学中，教师首先让学生利用原有知识经验进行探究，初步感知数学现象的共同特征；其次，在探究的过程中让学生经历观察、比较、分析、概括的过程，从具体到抽象，培养学生的合情推理能力；再次，建构规律，让学生去验证，在得出规律以后，教师要基于学生的视角去验证、去证明、去解释；最后，教学“你发现了什么”的主要目的是让学生研究数学方法，促进学生思维能力的提高，因此需要引导学生回顾和反思，总结活动经验，进而内化学习数学的方法。

三、对这类问题的再思考

1．问题驱动，激励学生探究

《义务教育数学课程标准（2011年版）》指出：“数学教学要着重培养学生的数学核心素养，让学生学会从数学的角度来分析问题，用数学的思想方法来解决问题。”因此，教师要改变传统的教学方式，鼓励学生质疑问难，引导学生从不同的角度提出有价值的数学问题，从而深入思考。例如，对于四年级上册第41页“做一做”的第2题，当学生量出两个角的度数后，教师可以这样引导：“通过刚才的操作，你有什么问题吗？”学生会提出“角的大小与边的长短有关吗？”“角的大小到底与什么有关？”等问题。又如，在教学完四年级上册第79页第10题、第80页第18题、第82页第4题后，教师可以提出：“通过刚才的规律，你有什么问题想说吗？”学生会说：“原来除数是两位数的除法，书中说‘一般’用‘四舍五入’法试商，我认为还可以根据实际情况使用口诀‘同头无除商八九，除数折半估商五’试商。”这样，学生在提出问题、分析问题和解决问题的过程中，逐步掌握学习数学的策略方法，进而提高学习能力。

2．数形结合，引发深刻的理解

《义务教育数学课程标准（2011年版）》明确指出：“几何直观主要是指利用图形描述和分析问题。借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。几何直观可以帮助学生直观地理解数学，在整个数学学习过程中都发挥着重要的作用。”如四年级上册第68页的第10题，教师可在学生学习了三角形的内角和知识后再一次呈现，分别将四边形、五边形、六边形……分成若干个三角形，学生就能发现多边形的内角和是180°×（边数-2）。

又如：如果 1＝12，1＋3＝22，1＋3＋5＝32，那么 1＋3＋5＋7＝（ ）2，1＋3＋5＋7＋9＋11＋13＝（ ）2。

教师可以启发学生从数与形的联系中探索规律。因为教学的目的不是简单地让学生利用加法运算得到答案，而是引导学生通过发现规律解决问题，学会思考。

3．适度拓展，促进思维的发展

《义务教育数学课程标准（2011年版）》指出：“义务教育阶段的数学课程，强调从学生已有的生活经验出发，让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程，进而使学生获得对数学理解的同时，在思维能力、情感态度与价值观等多方面得到进步和发展。”教师要读懂教材，用好教材，适当增加一些“你发现了什么”的问题，培养学生发现规律和运用规律的能力。例如，当学生学习了长方形和正方形的面积以后提出“运用长方形和正方形的面积能不能解决计算中的问题？”时，教师可以出示“小明在计算乘法时，误把6写成了9，结果积多了27，正确的积是多少？”“121×121-120×120”等习题，并提问：“你能借助长方形和正方形的最大面积画图解决以上问题吗？”又如，教学两位数乘法后，教师可以出示习题：一条铁丝长40厘米，将它围成一个边长是整厘米的长方形，怎样才能使面积最大？最大面积是多少？你有什么发现？你的发现还能用到其他的地方吗？请写出来。对于这道习题，一位学生是这样写的：

今天刘老师给我们布置了这样一道题∶一条铁丝长40厘米，将它围成一个边长是整厘米的长方形，怎样才能使面积最大？最大面积是多少？你有什么发现？你的发现还能用到其他的地方吗？请写出来。

如果长方形的长、宽、面积分别为 A、B、S，则 A＋B＝40÷2＝20（cm），列表如下：

A B S A B S 1 19 19 11 9 99 2 18 36 12 8 96 3 17 51 13 7 91 4 16 64 14 6 84 5 15 75 15 5 75 6 14 84 16 4 64 7 13 91 17 3 51 8 12 96 18 2 36 9 11 99 19 1 19 10 10 100

从上表可以看出,面积最大为100平方厘米，即当长为10厘米、宽为10厘米时，面积最大。通过观察得到这样一条规律：长和宽越接近时，面积越大；长和宽相等时，面积最大。用一句话归纳∶周长相等的长方形和正方形，正方形的面积更大。

这个规律也可以用来解决这道题：下面四道算式的积，谁最大？

30×20 25×25 31×19 26×24

因为四道算式的两个因数的和都是50（一定），25×25构成的是“正方形”，所以25×25的积最大，即两个因数的和一定，因数相差越小，积越大,所以 25×25＞26×24＞30×20＞31×19。

正如弗赖登塔尔所说：“数学学习是一种活动，这种活动与骑自行车一样，不经过亲身体验，仅仅从看书、听讲解、观察他人的演示是学不会的。”在“数与代数”领域中探究数的规律，不能游离于数的认识，要把数的关系与空间形式结合起来。在“图形与几何”的探究中，要结合具体的内容，渗透推理的方法，关注学生的几何思维的发展。“你发现了什么”的教学是一个让学生经历操作、观察、讨论、验证、应用的过程，是一个促进过程性目标达成的过程。因此，教师要充分利用好教材，让学生在探究中掌握科学的探究方法，从而提高学生的数学素养。