策略分析，优化提升——高中数学不等式高考试题分析与教学策略研究

江苏省常熟外国语学校 孔令华

不等式在高中数学知识体系中占据着重要地位，与函数、方程、数列、立体几何等知识都有一定的交集，并对学生的问题解决能力产生着极大影响，是检验学生学习情况的重要介质。鉴于不等式的重要作用，近年来，高考试题中也逐渐加大了不等式题型的所占比重，这些试题涵盖了不等式的概念、解法、证明、线性规划等多项内容，考验着学生对不等式知识的掌握程度，同时也检验着教师教学策略的有效性。对近年来高考试题中出现的不等式问题进行全面分析，其目的是为了制定具有针对性的教学策略，籍此以最大限度发掘不等式的教育潜力，培养高中生的学科素养。本文现结合教学实践，围绕高考试题分析与教学策略探究两个维度进行探究。

一、高考试题中不等式问题的考查分析

近年来，高考试题中逐渐增多了不等式考题。以2015年高考为例，统计发现，2015年全国卷理科考试中与不等式相关的试题约占全部试题总数的18.5%，试题以必修作为考试的重点对象。其中，不等式概念类试题约占不等式试题总数的2%；解不等式类试题占不等式试题总数的36.7%；证明不等式类试题占不等式试题总数的8.2%；含参数不等式的成立问题占不等式试题总数的18.4%；线性规划类问题占不等式试题总数的16.3%；基本不等式类占不等式试题总数的10.2%；取值范围和最值占不等式试题总数的8.2%。

具体形式方面，很多试题是与其他知识相结合后再求解的题型，如不等式与函数结合、与数列结合等等。

试题分析：答案B。这是一道典型的关于不等式性质的试题，这道题的特别之处在于它将函数与不等式相结合，考验学生在面对实际问题时能否灵活运用知识以及能否正确处理函数与不等式的关系。由此可见，每一项知识都不是独立的，在教学过程中，教师需将不同类型的知识进行糅合，着力于培养学生的数学思维，而不能让学生通过死记硬背来掌握知识。

例2 （2011上海卷·理15）若 且 ，那么，下列不等式关系中恒成立的是（ ）

试题分析：答案为D,这道题属于不等式的应用这一范畴，考验的是学生对不等式知识的掌握情况，包括不等式应用和成立条件的判断等等。题的特点在于它将“ ”这一关键条件置于题的第二项，一旦学生在读题时忽略这一关键，则必将影响解题的结果。因此，在教学实践中，教师应引导学生善于观察和思考，对不等式的各项构成要素进行充分的揣摩和掌握，从而提高问题解决能力。

试题分析：这道题也是一道典型的不等式求参类试题，通过读题可知，试题仍然是将不等式与函数相结合，通过函数性质、最值问题与不等式恒成立问题的相互作用来加强解题的难度。然而，这道题却有着很多种解法，而关键在于学生是否具备化归思想，能否化繁为简，找准解题的切入点。因此，教师在教学中需要引导学生反复进行一题多解的尝试，籍此让学生掌握数学的思想方法，从而提高解题效率。

通过上述高考中出现的三道不同类型的不等式试题可以看出，目前高考评测学生的主要标准已不再是“知识储备”和“临场发挥”，而是“数学思维”和“问题解决”。其中，数学思维是解决一切数学问题的“万能钥匙”，而“问题解决”则强调知识的灵活运用，两者相辅相成，是检验学生学科素养的重要依据。因此，高中数学日常教学的设计和组织也应针对高考试题有所调整，将培养学生的数学思维和问题解决能力作为一项常态任务纳入教学目标体系，从而提高教学质量，推动学生不断发展。

二、高中数学不等式的教学策略探究

1.基于数学思维培养的不等式教学设计

数学思维的形成是一个逐渐积累的过程，因此，数学思维的培养也应由浅至深，通过让学生掌握解决数学问题的思想方法，形成数学思维，提高学科素养。

以“解一元二次不等式”教学为例，对于这一课，学生们之前曾学习过一元一次不等式的解法，那么，在学习一元一次不等式时运用了哪些数学思想方法？是否可以运用相同的方法来解一元二次不等式？带着疑问，笔者以解一元一次不等式为突破口，让学生通过回顾旧知识来发现数学思想方法的共通性，籍此形成数学思维，提高问题解决能力。

在课堂开篇，笔者首先设计了探究小课题：一元一次不等式与一元一次方程和一次函数的关联。

探究过程：

（1）以多媒体展示函数图象：

x 2 2.5 3 3.5 4 4.5 5 y -3 -2 -1 0 1 2 3

分析上表可知：

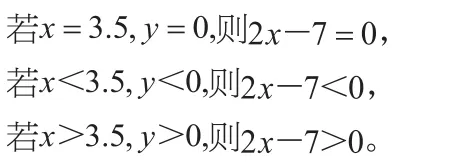
（3）提问：如何运用数学思想方法列式？

（4）学生合作探究。

利用数形结合，可得出结论：

解集为……

如此，则让学生们归纳出了解一元一次不等式所用的数学思想方法，而在此基础上，笔者导入新课，再围绕解一元二次不等式设计探究小课题。

师：前面的探究主要针对的是三个“一次”之间的关系，那么对于三个“二次”，即一元二次不等式、一元二次方程和二次函数的关系，又该运用怎样的探究方法？

探究过程：

（1）多媒体展示函数图象：

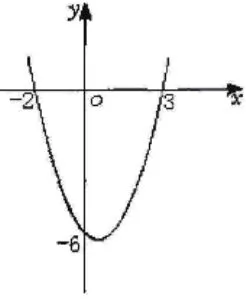
x -3 -2 -1 0 1 2 3 4 y 6 0 -4 -6 -6 -4 0 6

结合上表分析：

（3）合作探究：再次利用分析三个“一次”时所运用的数形结合的思想方法，分析一元二次不等式的解集，则结果如下……

综上所述，通过新旧知识的相互印证，使学生们体验了数学思想方法的共通性。通过两次解题的对比，学生们自然而然地会对“数形结合”这一思想方法产生深刻印象，从而形成“数学思维的作用大于知识储备”这一观念，由此则培养了他们的数学思维，加强了日常教学与高考试题之间的联系。

2.基于问题解决培养的不等式教学设计

通过分析高考中关于不等式的相关试题可知，问题解决是考验学生综合能力的一项重要标准。高考试题惯于将不同类型的知识相结合，其主旨不是为了检验学生的知识量，而是检验学生是否具备灵活运用知识的能力，因此，在教学中，教师需将培养学生的问题解决能力作为一项重点目标来加以落实，让学生能够学有所用，提高数学素养。

在实践中，教师可将解不等式与生活实际联系起来，将解不等式的过程转化为解决生活实际问题的过程，以此来培养学生的问题解决能力。

如题：某渔场为扩大产量，计划建造一个新养鱼池。新池容积为4800m2，深度为3m，假设新池的池底每平方米预算为150元，池壁每平方米预算为120元，那么，怎样设计才能将使造价最低？预算最低价为多少？

针对这道题，教师需要让学生首先将实际问题抽象为数学问题，继而让学生们运用自己熟悉的解不等式的方式来归纳答案，而学生解不等式的过程，即是培养问题解决能力的过程。

此外，教师还可直接引用发生在学生身边的一些具体实例，让学生通过分析将实例抽象为不等式。例如：质检部门规定酸奶中脂肪含量不得低于2.5%，蛋白质含量不得低于2.3%，而怎样才能将两个数据抽象为不等式组？通过这些生活化问题，能让学生在潜意识里将数学与生活联系起来，形成知识应用意识，提高问题解决的能力。

严格来说，高考试题是高中数学不等式教学的“风向标”，它隐含了社会发展对学生素质提出的要求，因此，考查高考试题的类型和特点，为日常教学提供参考依据，是提高教学质量、推动学生不断成长的重要途径。