巧用数形结合法破解绝对值函数的最值

浙江省宁波市第四中学 (315016) 蒋亚军 魏定波

这是2017年浙江高考数学第17题，涉及绝对值函数的最值问题历来受到竞赛、自主招生、高考命题者的青睐，它的解法离不开分类讨论，这种通法明显比较繁琐，本文从另一角度——“数形结合”法破解这类问题.

1 构建主元函数的图像

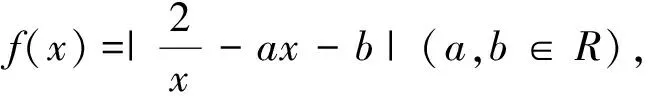
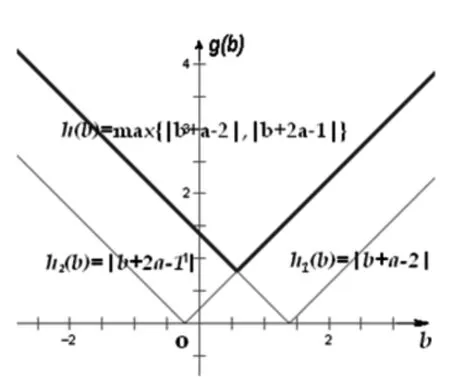
图1

解析:所求问题等价于求函数y=f(x)在[1，2]上的最大值，由于a>0，f(x)max=max{f(1)，f(2)}=max

{|a+b-2|，|2a+b-

1|}(如图1)，记g(b)=max{|a+b-2|，|2a+b-1|},依题意得g(b)≥m.

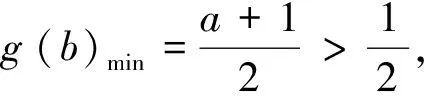
例2 (2015年高考(湖北卷)文科第17题)a为实数，函数f(x)=|x2-ax|在区间[0,1]上的最大值记为g(a).当a= 时，g(a)的值最小.

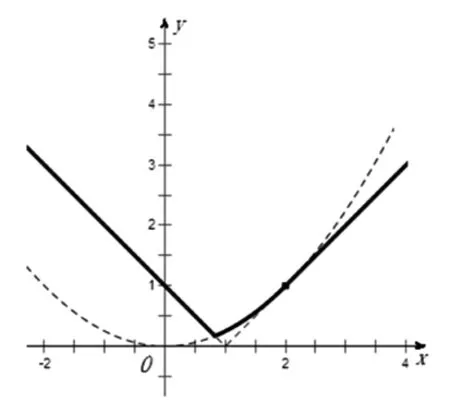
图2

评注：对于数学中的多元参数问题，若按常规思路确定主元，可能导致问题复杂化，此时，若能针对题目的结构特征，改变思考的角度，选择其参变量为主元，另辟蹊径，往往可使问题化难为易，结合相关的思想方法，迅速获解.

2.发挥图形的直观功能

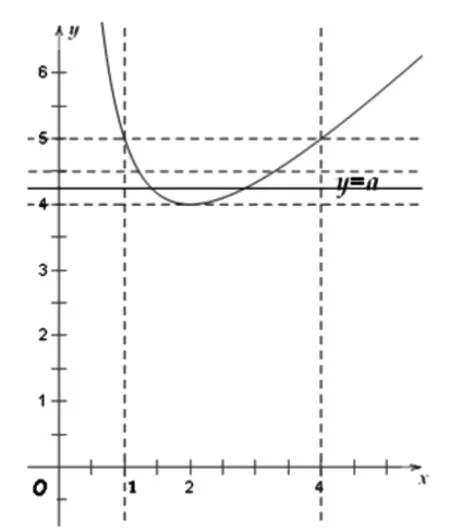
图3

解析:考虑到f(x)=

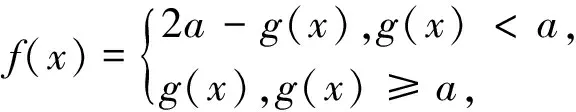
例4 (2011北约自主招生试题)求|x-1|+

|2x-1|+|3x-1|+…+|2011x-1|的最小值.

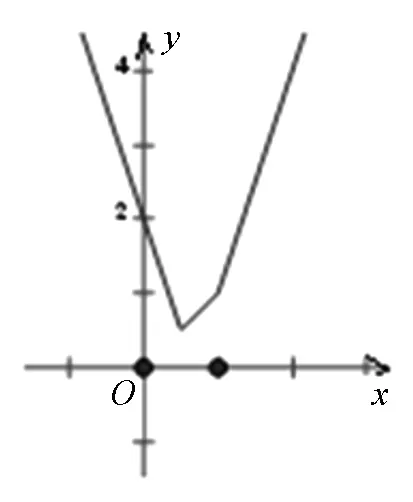
图4-1

解析:设f(x)=|x-1|+|2x-1|+|3x-1|+…+

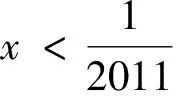
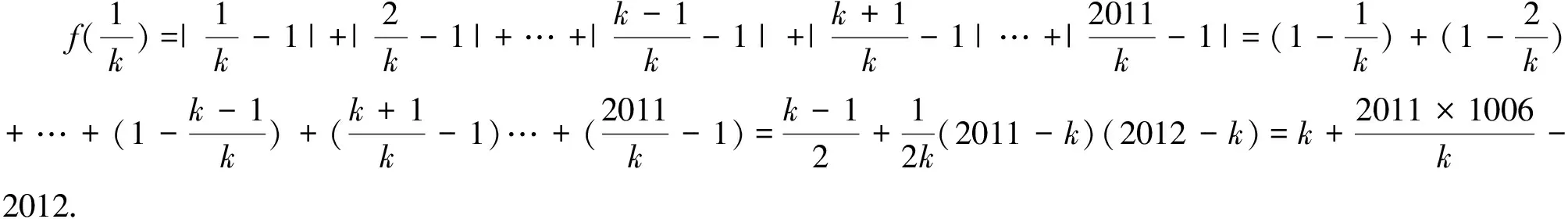
图4-2

由于函数y=x+

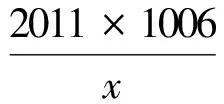
评注：2003年颁发的《普通高中数学课程标准(实验)》中明确提出“高中阶段的数学教学应加强几何直观教学，重视几何图形在数学学习中的作用，鼓励学生借助直观来思考”.运用几何直观来思考，解决最值函数的性质问题，省去了繁琐的参数讨论和复杂的计算过程，显得更加直观与简单.

3.借助函数的逼近模型

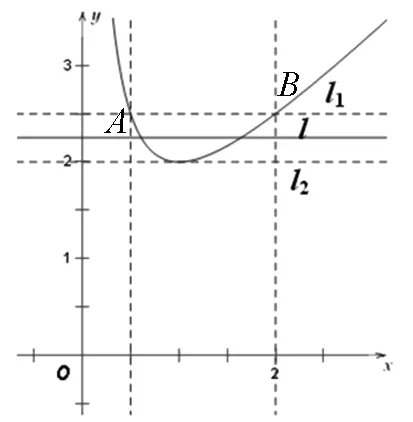
图5

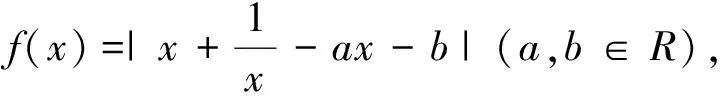
图6

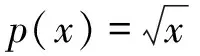
评注：上述问题的实质是俄罗斯数学家切比雪夫的最佳函数逼近问题，虽然超出了目前教学大纲，但是我们借助熟悉的“线性回归”的思想，通过直观图形容易找出p(x)的最佳一次逼近q(x)=ax+b来.这样一来，一个多参数的最值函数问题达到有效的、简单的解决.

4.运用线性规划的方法

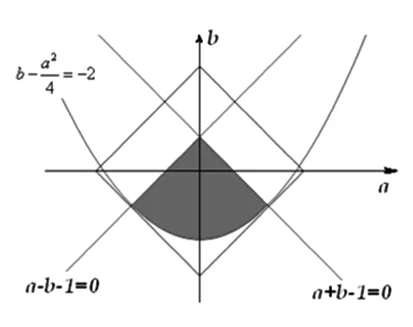
图7

例7 (2015年浙江省高考数学(理)科第18题)已知函数f(x)=x2+ax+b(a,b∈R)，记M(a,b)是|f(x)|在区间[-1,1]的最大值.

(Ⅰ)证明：当|a|≥2时，M(a,b)≥2；

(Ⅱ)当a，b满足M(a,b)≤2时，求|a|+|b|的最大值.

解析:对于(Ⅰ)可以用构建主元函数的图像的方法解决.

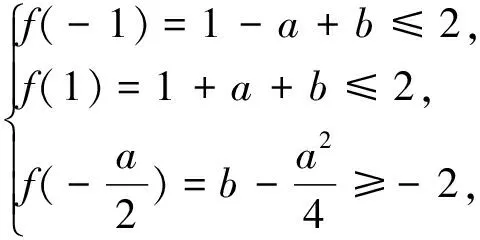
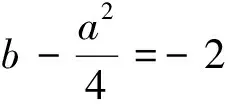
评注：解决二次函数中多个参数的综合性问题，借助线性规划的原理，运用数形结合的思想方法是不错的选择，它能避免一些复杂的不等式转换，改变学生的思维定势.