一维Rydberg原子—腔系统

晏 浩 纪安春 孙 青

(首都师范大学物理系，北京 100048)

0 引 言

过去几十年来，量子多体问题和量子相变的研究在凝聚态物理学中得到了广泛的关注.随着量子光学的发展和超冷原子物理学的兴起，原子与光场相互作用的研究变得越来越有趣和重要，并受到了很多理论工作者和实验工作者的青睐.特别是在20年代的物理学成果中，玻色—爱因斯坦凝聚(BEC)在理论上的发现和实验上的实现，进一步推动了原子与场相互作用领域的发展与壮大.

原子与光场相互作用的研究在量子光学、超冷原子物理和凝聚态物理中都占有非常重要的地位，而且关于量子相变很多方面的特性在理论和实验两个角度都已经出现了很多理论成果和实验成果.在著名的Dicke模型中，当考虑到一种两能级冷原子气体与光学腔耦合时，原子与光相互作用的非局域相干性就很好地支持了相变理论中的超辐射(SR)相变观点，而且许多先前的研究已经表明，不同的量子相特征的显示与不同的参数调校关联性很强[1-4].

在这篇文章中，我们研究了固态相、超流相(SF)和超固态相(SS)之间的相边界问题以及给出了相应的基态、激发态能量表达式.我们考虑的模型是两能级的里德堡原子与光学腔的耦合系统，对原子考虑了它们之间偶极—偶极相互作用的最近邻项(C6).我们从三个不同角度对系统模型进行处理，分别是平均场理论、强耦合展开和量子Monte Carlo模拟，由此给出了相应的全参数空间的量子相图.

1 哈密顿模型

我们考虑的哈密顿量可如下表达：

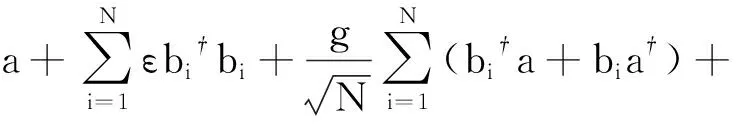
(1)

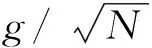
当g为零时，哈密顿量是对角化的，此时可以解析求解.简化哈密顿量后，方程(1)变为上式中μa=μ-ω和μb=μ-ε代表有效化学势.为了避免光子数出现无穷大，我们假定μa和μb均小于零，也就是没有里德堡原子处于激发态.当增大μb至大于零而小于2C6时，只有子晶格原子在近邻排斥作用下跳跃到激发态上，而当μb大于2C6时，源于化学势的能量增益能够克服排斥能，进而导致系统进入Mott绝缘态.为了解决这个问题，可以选取有限的g值跳跃，并采用平均场理论、强耦合展开和量子蒙特卡罗模拟进行处理.

(2)

2 平均场理论

平均场理论下系统波函数如下给出：

(3)

其中 |0〉是系统真空态，代表所有的原子都处在基态上，λ和θ都是可变参数.为了找到基态能，我们需要对每个位置的平均场能量求极值：

EMF≡ 4〈λ,θ|H|λ,θ〉/N+Const

=-gλ(sinθA+sinθB)-μaλ2-(μb-C6)·

(cosθA+cosθB)+C6cosθAcosθB．

(4)

这里我们假设对不同子晶格A和B来说θ是相同的.

图1 平均场理论得到的相位图，图(a) Δ=3, 图(b) Δ=2, 图(c) Δ=1 和图(d) Δ=0.5 均取 C6 为单位长度

由于μa远大于零时λ无限大，故我们只考虑μa<0的情况.因此，我们对平均场能量EMF求极值时取λc=-g(sinθA+cosθB)/(2μa)，因为它是λ的二次函数.将λc带入到平均场能量EMF中可得：

EMF= -g2(sinθA+sinθB)/(4μa)-(μb-C6)·

(cosθA+cosθB)+C6cosθAcosθB.

然后通过数值模拟的方法，分别就上式中θA和θB对能量求极值，由此可得图1所示的全参数空间的相图.

图1中，Mott-0 和 Mott-1分别标识Mott绝缘态没有占据和完全占据两种状态.首先，我们定义Δ=μb-μa作为化学势失谐量，当Δ大于Δc1=2C6时，Mott-0 和 Mott-1 两种状态同时存在；当Δ小于Δc1时，只有Mott-0状态存在.其次，在逐渐减小Δ的过程中维持(π,π)电荷密度波(CDM)的固态相叶会收缩，直到Δ小于零时系统中只存在Mott-0状态和超流相(SF)状态.

系统的临界相是超固态相(SS)，它能够维持(π,π)CDM并且是可压缩的，然后通过计算不同子晶格的平均场密度ρ=cos(θ/2)2=(cosθ+1)/2，能够发现它们之间的差异大于0而小于1.因此它既不是固态相也不是超流相.

为了更好的理解相变问题，我们利用强耦合展开分析Δ>Δc区域的临界线问题.

3 强耦合展开

在强耦合g≪C6区域，我们将交换项作为对角部分的微扰来处理，所以我们就可以利用熟悉的量子力学微扰理论来计算临界线，也就是比较基态能量和准粒子激发态能量.

(5)

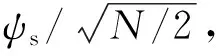
(g2/Δ+g2/(Δ-2C6))/2,

(6)

因此其临界线为μbc3=2C6-g2/(2Δ-4C6).

Em1= -(μb-C6)N+μb-2C6-

(7)

所以临界线为μbc4=2C6+g2/(Δ-2C6).同样对于粒子激发来说，其零级波函数ψm1=a†ψ1，所以其二级能量为：

(8)

通过比较得到的能量即可知道我们所求的临界线为μac=-g2/(Δ-2C6).

从临界线的表达式出发我们可以看出不同的不可压缩的状态的叶片会随着Δ的增加而收缩，这种特性是合理的，因为很大的化学势失谐量 Δ 可以减少二级跳跃.为了详细地搞清楚不同相及其相边界问题，我们运用随机级数展开来模拟系统，这种展开也是一种量子蒙特卡罗的算法模拟.

4 量子蒙特卡罗

从图2可知，在半填充固相和超流相之间存在着一种居间相，它具有有限的结构因子和可压缩性，这种压缩性具有很小的有限尺寸影响.如果其密度低于一半，我们便可确信这是一种由空穴激发而诱导的超固态相(SS).

图2 结构因子 S(Q)/N(实线)和压缩性 κ∕10(虚线)，其中已取 C6=1 和Δ=3，并考虑不同温度和尺寸 β=100,L=100(圆状)，β=100,L=150(方状)和 β=500，L=150(三角状).插图为平均密度ρ

接下来我们看看不同的相变问题.从图3的左侧我们可以发现超固态相能稳定地存在于固相和超流相之间，并且它的区域几乎不受Δ影响.与之相比，粒子激发诱导的超固态相表现出相同的性质.类似于三角晶格中得到的超固态相[5]，这里的超固态相与固态相之间的相变属于二级相变，而超固态相与超流相之间的相变则属于一级相变.由于图3中横轴是用μbc2和μbc3调谐定标的，所以很容易得出固态相叶会随着Δ的增加而出现收缩，这与我们用平均场理论得出的结果一致.

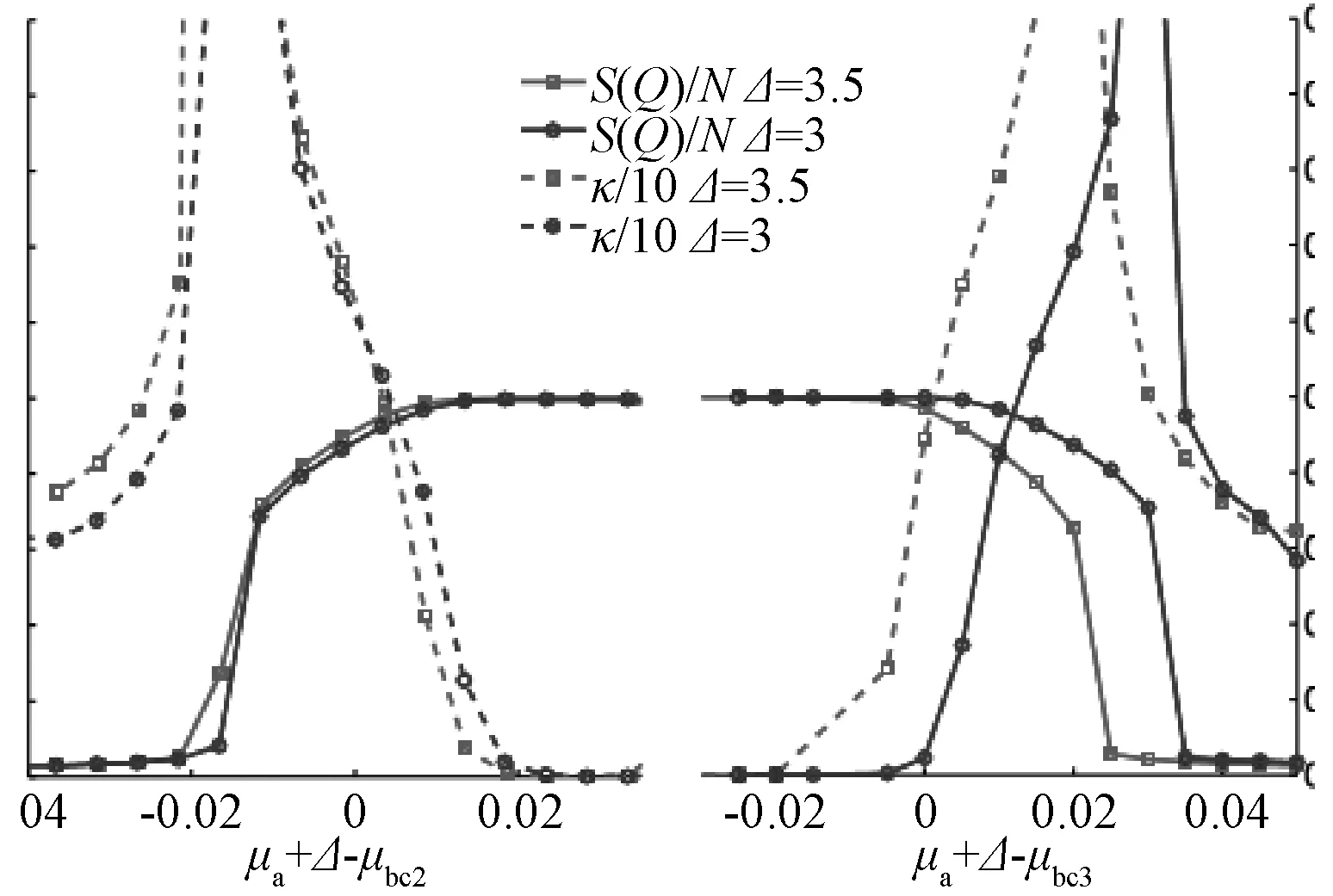
图3 结构因子 S(Q)/N(实线)和压缩性 κ∕10(虚线)，其中已取 C6=1， g=0.8(0.6)，β=100， L=100 分别代表左侧(右侧)，同时左、右侧分别是空穴激发和粒子激发

在图4中我们得到了Δ=3 时的相图，其临界线很好地吻合了先前强耦合展开工作中的结果[5-6].依据平均场理论的预测，由粒子激发诱导的超固态相的区域要较小于空穴激发诱导的区域，然而两者的超固态相区域都很窄，这种性质同考虑次近邻相互作用的方形晶格得到的超固态相很类似[7].

图4 由三种方法平均场理论、强耦合展开和量子蒙特卡罗模拟得到的相图，已取C6=1 和 Δ=3

5 结 论

本文主要研究的是一维情况下里德堡原子与腔场相互作用的系统，通过平均场理论、强耦合展开和量子蒙特卡罗模拟，我们得到了全参数空间的相图.除了Mott绝缘态之外，我们不仅发现了π电荷密度波的部分填充固态相，当交换项g值很大时还发现了超流相，最重要的是发现了位于固态相与超流相(SF)之间的稳定的超固态相(SS).

同时，粒子激发诱导的超固态相相比空穴激发诱导的更加不稳定，最后我们还发现前面文中定义的化学势失谐量Δ强烈地影响着不同相的存在和形状.