控制力矩陀螺MIMO解耦控制实验

2018-07-27钱玉恒王佳伟杨亚非

实验室研究与探索 2018年7期

钱玉恒，王佳伟，杨亚非

(哈尔滨工业大学飞行器控制实验教学中心,哈尔滨 150001)

0 引言

随着航天科技高速发展，航天器种类愈加繁多，用途愈加广泛，精度与稳定性要求越来越高，要达到航天器高精度要求，姿态稳定性控制是基础。航天器的姿态控制一般采用控制力矩陀螺(Control Moment Gyroscope，CMG)作为执行器[1-4]，如国际空间站应用的单框架力矩陀螺或双框架力矩陀螺，需要配置力矩陀螺构型，使多个陀螺可协同动作，进而实现姿态控制作用。目前有近400个航天器采用CMG作为姿态控制系统的主要执行器，我国天宫一号和二号已使用CMG作为飞船执行机构[5-6]，与此同时，针对CMG的有关研究成果越来越多[7-10]。美国ECP公司生产的Model 750型CMG是一种能够全面验证力矩陀螺特性的实验装置，已应用到众多世界知名大学，促进了对力矩陀螺的研究和教学。通过对CMG数学模型分析发现，陀螺框架之间存在耦合力矩，转盘旋转速度的变化会对外框架形成力矩干扰，造成外框架的速度波动，而内外框架的耦合又会影响外框架速度精度，进而影响输出力矩精度。针对力矩陀螺的耦合问题，已经有文献提出一些解耦方法[11-12]。

本文首先介绍Model 750 CMG的结构及数学模型，随后对轴锁定时CMG单轴控制的有效性和局限性展开了控制方法实验分析，这种单轴控制方法在轴自由状况下无法取得较好的解耦控制效果。文中结合系统耦合二阶模型特点，针对CMG的多轴耦合问题，采用了最优控制方法实施解耦控制实验，实验表明该方法解耦控制有效。

1 实验装置组成及数学模型

1.1 实验装置组成

实验装置由机电部分、控制箱、运动控制卡及应用程序组成。

(1) 机电部分是力矩陀螺主体，如图1所示。主体部分有4个旋转轴，转子D和框架C、B、A分别绕轴1～4旋转，每个轴安装的编码器分别测量各轴角位移；永磁直流伺服电动机1带动大惯量转子D旋转，提供输入惯量，永磁直流电动机2通过绞盘皮带驱动框架C旋转，输入控制力矩，框架C、B、A分别带有滑环。

图1 机电部分

(2) 控制箱是运动控制卡和机电部分之间的接口部件，主要含电动机驱动、编码器检测、接口匹配及安全措施(惯性开关、制动器)等部分。

(3) 运动控制卡的核心任务是执行实时控制程序，起到控制器作用。支持数据采集、安全检测、状态判断，可输出各种控制信号。运动控制卡可接收和解释计算机发出的程序指令，也能通过数据总线向计算机发送数据。

(4) 应用程序依托计算机，支持“类C”语言的控制器设计、轨迹定义、数据采集、绘图系统、执行指令等。丰富的底层函数和良好的人机界面为装置提供了一个非常强大的实验环境。

1.2 数学模型

CMG框架坐标系如图2所示[13]，组成转子D和框架C、B、A 4个固连坐标系，对应的4个转动轴为1～4轴。其正交单位向量分别为di，ci，bi，ai(i=1,2,3)，设置惯性参考坐标系N的正交单位向量为Ni(i=1,2,3)，每个坐标系均满足右手定则，q1定义为D在d2方向的角位移；q2定义为C绕c1相对B的转角；q3为B绕b2相对A的转角，q4被定义为A绕a3相对N的转角，这4个角度确定了系统的构形，图2的构形对应角度为qi=0(i=1～4)。

图2 控制力矩陀螺框架坐标系

系统所有部件的质心位于转子D中心，它也是所有框架轴的中心。在只考虑旋转动力学情况下，相对于其各自的坐标系，给出主惯性矩阵如下：

(1)

式中：Ix,Jx,Kx(x=A,B,C,D)分别表示部件A、B、C和D中绕各自第i(i=1,2,3)方向的转动惯量。

定义A在N中的角速度：

NωA=ω4a3

(2)

同理，定义以下角速度

AωB=ω3b2，BωC=ω2c1，CωD=ω1d2

(3)

则角速度关系式为

(4)

每个坐标系都可以通过转换矩阵转换到惯性坐标系。考虑到由C施加于D的转矩T1，以及由B施加于C的转矩T2，有：

(5)

式(1)～(5)唯一地确定系统的动力学方程。通过拉格朗日方程可以求解运动方程，其形式为:

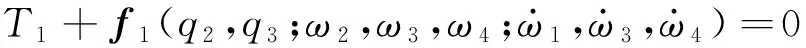
(6)

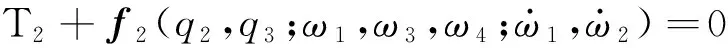
(7)

(8)

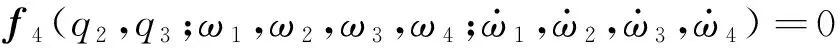
(9)

根据方程(6)～(9)在操作点附近的泰勒级数展开式的前两项，就可求出其线性化运动方程。稳定平衡点被定义为ω1=Ω，q2=q20，q3=q30，则线性化方程为:

(10)

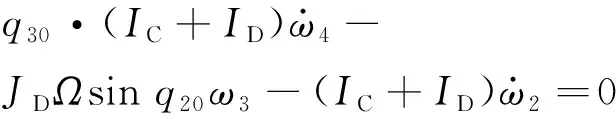
(11)

JDΩsinq20·ω2-JDΩsinq20sinq30·ω4-

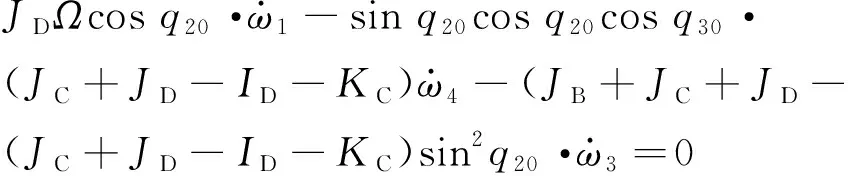
(12)

JDΩsinq20sinq30·ω3-JDΩcosq20cosq30·ω2+

(ID+KA+KB+KC+(JC+JD-ID-

KC)sin2q20+sin2q30

(IB+IC-KB-KC-(JC+JD-ID-KC)·

(13)

式(10)～(13)表示CMG在任意操作点下，各种构形的线性动力学，式(10)～(11)为驱动方程，式(12)、(13)为约束方程，式(10)～(13)简化为状态方程：

(14)

式(14)表明，力矩陀螺各旋转轴之间存在耦合，控制系统完全是多输入多输出系统(MIMO)。

2 零平衡点双轴控制实验

(15)

式中，ω3和ω4已无耦合。对式(15)进行拉氏变换，得出下列传递函数：

(16)

q4/T2=

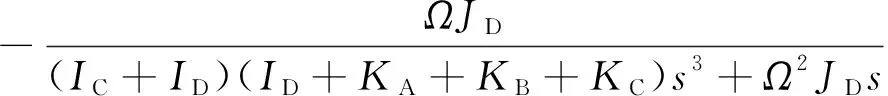
(17)

q2/T2=

(18)

将参数代入式(16)～(18)得:

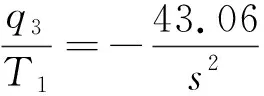
(19)

(20)

(21)

说明系统为单输入单输出系统，ω3和ω4之间无耦合。其中，q3/T1是大惯性对象的反作用陀螺力矩问题，大惯性对象属于典型对象，在锁定2、4轴时，采用PID方法控制单轴输出角度q3已获得较好控制效果[13]。而q4/T2是串级对象的控制陀螺力矩问题，在锁定3轴时，应用PID、极点配置和LQR等方法控制单轴输出角度q4，均取得较好控制效果，经过控制实验结果比较，LQR控制方法较其他方法具有更好的动态和静态特性[14]。

如果取消轴锁定条件，系统自由度变为4个，各轴旋转波动将会形成互扰耦合，如果实验初始位置正确(见图3)，互扰将会较弱，采用PID和LQR方法分别控制q3和q4，控制效果也是比较理想[15]。

根据式(16)，PID控制q3框图见图4。图中：r1、u1为控制算法输入和输出；KA3=-ke3ku1，负号表示转动方向相反；ku1=1.28×10-5为控制算法输出对应的扭矩T1输出增益；ke3=2 547×32为编码器3增益。

海事部门要积极与当地政府积极沟通协调，联合海洋渔业局等相关职能部门，加大对非法占用防台应急锚地的查处力度。充分发挥VTS、智慧海事监管服务系统的作用，结合现场执法，加大对锚地的巡航巡查，及时制止渔业养殖等非法占用防台锚地行为。协调地方政府相关职能部门对在锚地水域设置的养殖区进行清理整顿。开展联动执法，减少渔业养殖等非法用海活动对船舶锚泊带来的影响。

根据式(17)，LQR控制q4框图见图5。图中：

D(s)=(IC+ID)(ID+KA+KB+

KC)s3+Ω2JDs

(21)

图3 零平衡点双轴控制力矩陀螺的位置

图4 PID控制轴3框图

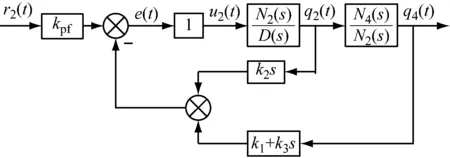
图5 LQR控制轴4框图

N2(s)=ke2ku2(ID+KA+KB+KC)s

(22)

N4(s)=-ke4ku2ΩJD

(23)

r1、u1为控制算法输入和输出；ke2=3 883×32为编码器2增益；ku2=9.07×10-5为控制算法输出对应的扭矩T2输出增益；ke4=2 547×32为编码器4增益；kpf为滤波器增益，r2(s)与q4(s)的匹配项。

同时输入幅值r1=r2=200的方波阶跃信号，双轴零平衡点控制经过反复调试。控制q3的PID参数确定为：kp=4.5；kd=0.89；ki=0。借助LQR参数优化思路，控制q4的LQR参数经寻优后，确定

K=[k1k2k3]=[-4.5 0.076 -0.23]

kpf=-4.5

控制曲线如图6所示。

图6 零平衡点双轴控制阶跃响应曲线

同理，零平衡点双轴控制斜坡跟踪曲线见图7。图中：r1为轴1控制输入；q3为轴3控制输出；r2为轴2控制输入；q4为轴4控制输出。

受框架不平衡力矩和框架轴承摩擦等影响，q3与q4存在互扰耦合。双轴阶跃响应曲线表明，q4的阶跃变化对q3交叉耦合略大；q3的阶跃变化对q4交叉耦合较少。双轴斜坡响应曲线在q4饱和情况下，对q3交叉耦合不明显。因此，在零平衡点处，上述PID、LQR控制方法可行。

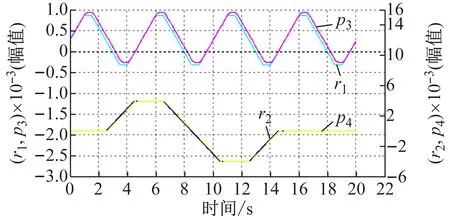
图7 零平衡点双轴控制斜坡跟踪曲线

3 非零平衡点双轴控制实验

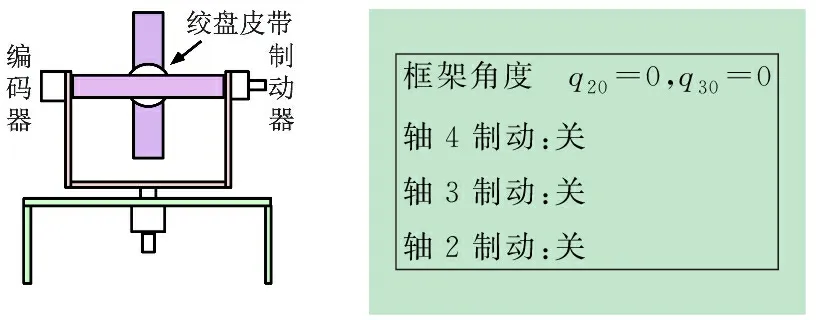
在零平衡点条件下，各轴之间的互扰轻微，采用普通的控制方法就能达到控制效果。根据实验现象，系统耦合随着非零平衡点角度增加而变大，在q2=20°和q3=-20°时(见图8)，耦合现象十分明显，这与式(14)的理论分析一致。将图8角度作为耦合控制实验位置能较好地反映控制的解耦效果，确定有效的控制方法和策略。为便于控制曲线分析，将q2=20°和q3=-20°初始位置的控制指令和编码器输出设置为零，即参量零化处理后，进行阶跃响应和斜坡跟踪响控制实验，观察控制效果。

框架角度 q20=20,q30=20轴4制动:关轴3制动:关轴2制动:关

图8 非零平衡点双轴控制力矩陀螺的位置

3.1 反作用力矩和陀螺力矩激励的双轴控制

仍采用上述双轴控制方法，非零平衡点反作用力矩和陀螺力矩激励的双轴控制阶跃响应和斜坡跟踪曲线如图9和图10所示。从图9、10可见，非零平衡点控制比零平衡点控制交叉耦合严重，特别是q3耦合极其明显。这是由于在陀螺力矩作用下，轴2旋转力矩将引起一个绕轴3的力矩，在q2≠0状况下，q2的变化会引起q3状态变化。同理，q4的速度突变，也会引起q3状态变化。这说明，反作用力矩和陀螺力矩激励的双轴控制方法在非平衡点处解耦效果不佳。

3.2 MIMO双轴解耦控制

考虑到力矩陀螺属性和实验现象，可判断出系统输出变量q3,q4,ω2,ω3,ω4均对耦合有影响。为此选取q2,q4,ω2,ω3,ω4作为状态反馈变量，从中分析各变量对耦合的影响程度。而式(10)～(13)表明，q3和q4之间的耦合呈现二阶系统特征，适合采用PD控制策略解耦，考虑到系统软件平台功能和实验的可实现性，结合实验教学效果等因素，最终选用LQR最优控制方法实施MIMO控制，利用求得最优状态反馈增益矩阵，获取最优控制律。最优多变量控制框图如图11所示。

图9 反作用力矩和陀螺力矩激励双轴控制阶跃响应曲线

图10 反作用力矩和陀螺力矩激励双轴控制斜坡跟踪曲线

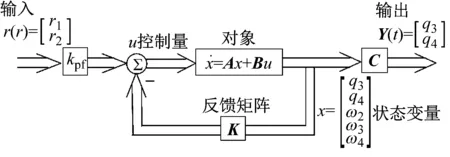
图11 最优多变量控制框图

LQR反馈控制律设计为u=-Kx，其中参数矩阵为

式中：k12、k15是控制q3输出的去耦合PD控制参量；k21、k24是控制q4输出的去耦PD控制参量，从中起到消减交叉耦合作用。

针对q20=20°,q30=-20°非平衡点模型，通过求解Riccati方程，使用LQR综合算法找到可以最小化代价函数J的控制器K，代价函数，

选择Q=C′C，使得预期输出q3和q4的误差最小，

解耦控制实验的难点在于反馈矩阵参数K调试，反复实验最终确定反馈增益矩阵

MIMO双轴解耦控制的阶跃响应和斜坡跟踪曲线如图12和图13所示。

图12 MIMO双轴解耦控制阶跃响应曲线

图13 MIMO双轴解耦控制斜坡跟踪曲线

反馈矩阵参数实验曲线表明q3,q4,ω4对参数耦合程度影响较为明显，反馈增益矩阵的q3,q4,ω4在反馈控制律中所占权重最大，反馈增益参数既起到了控制作用又发挥了解耦作用。对q20=20°，q30=-20°情况，由于引入LQR代价函数J使q4的误差最小化，当q4阶跃信号状态时，q3交叉耦合与前面控制方法相比减少很多。但受到q4带宽略增影响，对q3的阶跃输入时，q4的交叉耦合与前面控制方法相比有轻微增加。在斜坡跟踪控制效果图能看出，解耦控制跟踪效果很好。

注意，上述LQR解耦方法对PD控制有效的耦合关系解耦效果显著，对于复杂的耦合系统，LQR方法有效性需要实验验证。另外，本实验也可拓展至其他非零平衡点，获取更多非零平衡点最优控制参数，为其他智能化方法提供研究参考。