雷达辐射源信号识别特征参数集的构建方法

刘 飞, 何明浩, 韩 俊

(1.空军预警学院, 湖北 武汉 430019; 2. 中国人民解放军95174部队, 湖北 武汉 430040)

0 引 言

随着数据采集、存储、传输技术的快速发展,雷达辐射源信号(radar emitter signal,RES)识别方法逐渐从传统的信号脉冲描述字转向了基于脉冲波形数据的脉内特征参数[1-2]。因此,挖掘和提取更能表征RES的脉内特征参数成为研究热点,如:频谱特征[3-4]、时频特征[5-9]、双谱特征[10]、模糊函数特征[11-12]、相像系数特征[13]、熵特征[14-17]、复杂度特征[18]等出现在各文献研究中。各种脉内特征参数的挖掘应用一定程度上解决了传统识别方法中的错分误判问题,提高了雷达辐射源识别的准确率。

然而,脉内特征参数在工程应用中的一些局限性也慢慢涌现出来[19-20]。一个常见的局限性就是大多特征仅对限定调制类型的RES具有较好的识别性能,而难以识别其他调制类型的RES[21-22]。例如,时频特征对单载频信号、线性调频信号、非线性调频信号有很好的识别效果,但对频率编码信号和频率分集信号却无能为力;再如,模糊函数特征对频率编码信号和频率分集信号有很好的识别效果,但对非线性调频信号和线性调频加二相编码信号的识别率却并不高。另一个局限性是单个特征的识别率随仿真条件的变优而有趋于“边缘效应”的现象,不能突破自身识别率的“瓶颈”[23-24]。在特征提取仿真试验中,当特征维数达到一定值后,增加特征维数并没有带来明显的识别率收益,相反,提取较高维数的特征会显著提高识别时间成本。

针对上述问题,本文拟通过组合不同种类的特征,构建特征参数集,集聚各特征参数在不同调制类型RES中的识别优势,提升基于特征参数集的识别方法的通用性和准确性。

1 特征组合及性能分析

特征组合是指将两种及以上不同特征参数,通过特征数据的连接,变为一种新的特征的过程。给定两种分别为m维和n维的特征，即A={a1,a2,…,am}和B={b1,b2,…,bn},则他们可以按以下方式组合，即

[A,B]={a1,a2,…,am,b1,b2,…,bn}

(1)

或:

[B,A]={b1,b2,…,bn,a1,a2,…,am}

(2)

上面2种组合方式,仅是2种特征参数特征数据连接顺序的不同。由式可知,特征组合后的维数为2种对应特征的维数之和,即A和B的特征组合维数为m+n。

1.1 特征种类对识别性能的影响

讨论不同类型的特征参数组合对识别性能的影响。对引言中提及的7种特征进行仿真分析,仿真条件为:训练数据的样本量为3 500(每种特征500个),测试数据的样本量为700(每种特征100个),分类器为支持向量机(support vector machine,SVM),SVM核函数为径向基函数(radial basis function,RBF),RBF参数γ=0.200 0,惩罚系数C=0.100 0。

分别以每种特征为对象,与其他特征进行组合,特征组合性能仿真结果如图1所示,图1中,横坐标“1”至“6”分别代表其他特征,次序与频谱特征、时频特征、双谱特征、模糊函数特征、相像系数特征、熵值特征、复杂度特征一致。

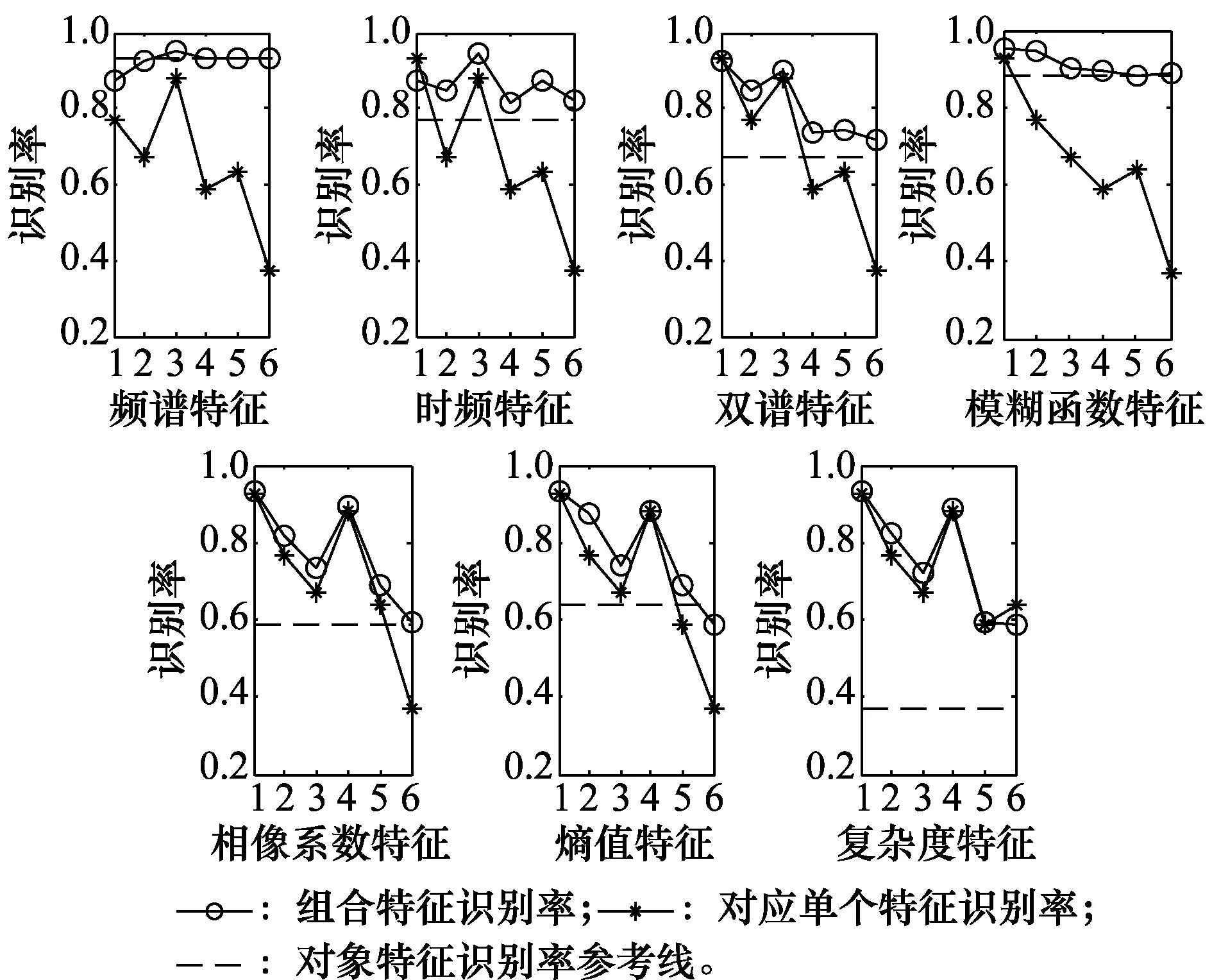
图1 各种特征与其他特征组合识别性能Fig.1 Recognition performance of various characteristics combined with other characteristics

由图可知,特征组合对识别性能的影响有以下3种情况:

(1) 组合特征识别率同时高于对象特征和其他特征,如双谱特征、模糊函数特征、相像系数特征,说明此类特征与其他特征的组合对双方均是有益的,属于互利型特征;

(2) 组合特征识别率高于对象特征而部分低于其他特征,如时频特征、复杂度特征,说明此类特征与其他特征的组合对自身是有益的,而对其他特征并不一定有益,属于利己型特征;

(3) 组合特征识别率高于其他特征而部分低于对象特征,如频谱特征、熵值特征,说明此类特征与其他特征的组合对其他特征是有益的,而对自身并不一定有益,属于利它型特征。

总体来说,组合特征的识别性能与单个特征相比是提升的,在仿真中没有出现组合特征识别率同时低于对象特征和其他特征的情况。

1.2 组合顺序对识别性能的影响

讨论特征分别按照式(1)与式(2)进行组合对识别性能的影响。将7种特征按频谱特征、时频特征、双谱特征、模糊函数特征、相像系数特征、熵值特征、复杂度特征的次序两两进行组合,由此得到的特征组合称为顺序组合;将上述组合的次序进行交换,由此得到的特征组合称为反序组合。在第1.1节的仿真条件下,各特征组合的顺序和反序识别率如图2所示。

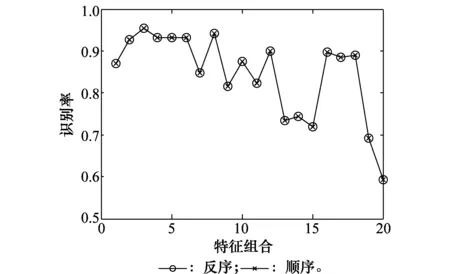
图2 特征组合顺序对识别性能的影响Fig.2 Effect of characteristic combination order on recognition performance

由图2可知,各特征组合的反序识别率与顺序识别率完全一致,说明特征组合排列次序的改变对识别性能是没有影响的。通过对其他特征组合方式的仿真验证,均有此结论。因此,特征组合式(1)和式(2)是等效的。

1.3 特征个数对识别性能的影响

讨论不同个数的特征参数组合对识别性能的影响。为讨论问题的完备性,将单个特征作为特征个数为1的情况纳入对比分析。根据特征组合公式,对于N种不同类型的特征参数,特征组合方式的总数为

(3)

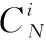
在对7种特征所有组合方式的性能分析中发现,特征组合可分为2种情况:

(1)优型组合,如i=2、i=3、i=5时,识别率排名第1的组合方式等,他们的识别率高于对应特征的其他所有组合情况,定义该类组合为优型组合。优型组合实现了特征参数识别率的提高,是在进行组合时最希望得到的结果。

以i=5中排名第一的组合为例,其对应特征为时频特征、双谱特征、模糊函数特征、相像系数特征、熵值特征,对应特征的其他所有组合与该组合的识别率对比情况如图3所示,图3中横坐标为其他组合序号,虚线为该组合识别率参考线98.43%。

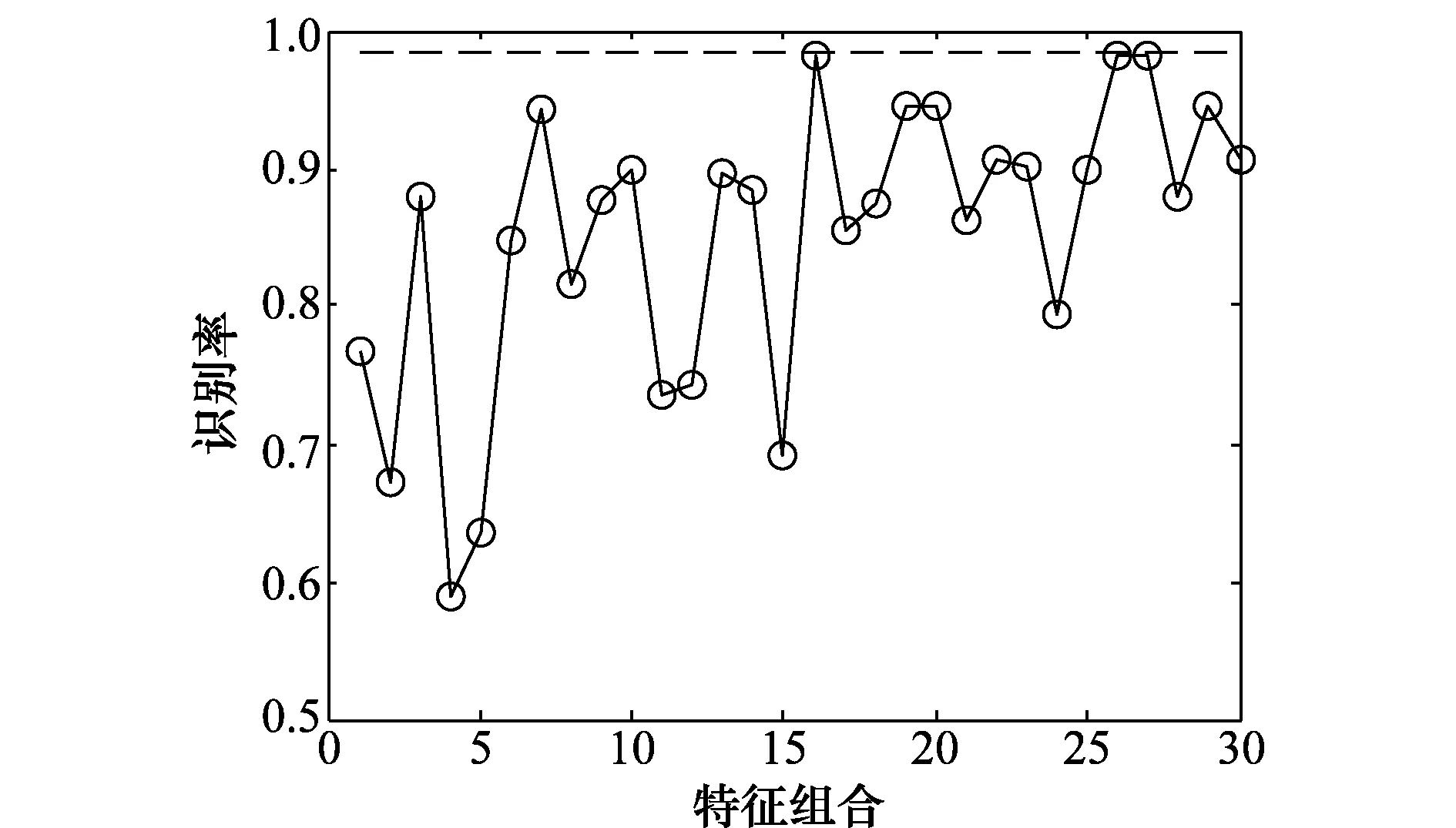
图3 优型组合示例图Fig.3 Example diagram of optimal combination

由图3可知,其他组合的识别率均低于该组合识别率,图3中接近虚线的3个识别率分别为98.29%、98.14%、98.29%,故该组合为优型组合。

(2)非优型组合,如i=2至i=7时,识别率排名倒数第一的组合方式等,他们的识别率低于对应特征的所有组合中的部分组合情况,定义该类组合为非优型组合。非优型组合并没有实现相对所有特征参数识别率的提高,所以在实际应用中往往舍弃这类组合。

以i=5中排名倒数第1的组合为例,其对应特征为频谱特征、时频特征、双谱特征、模糊函数特征、复杂度特征,对应特征的其他所有组合与该组合的识别率对比情况如图4所示,图4中横坐标为其他组合序号,虚线为该组合识别率参考线77.57%。

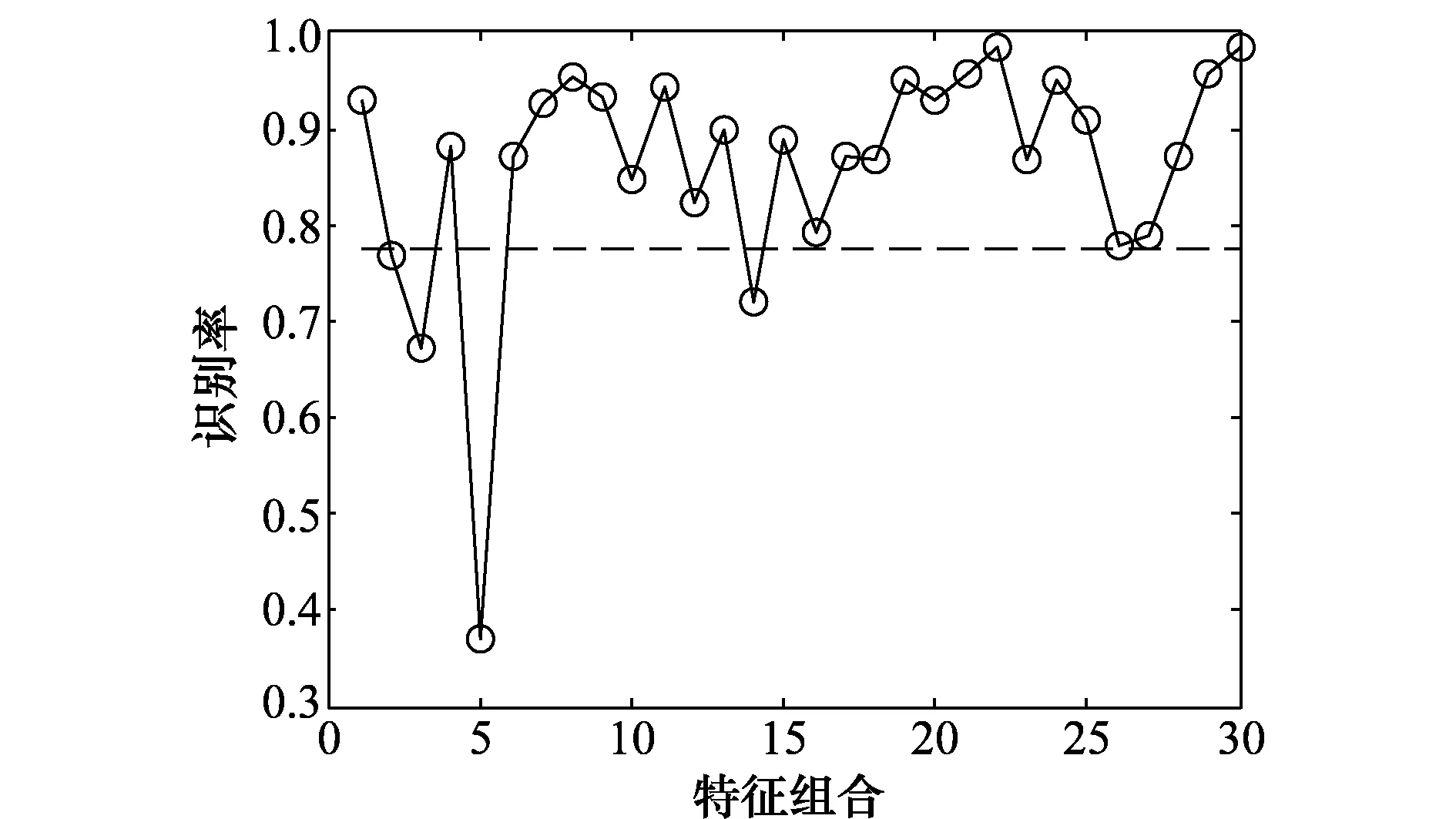
图4 非优型组合示例图Fig.4 Example diagram of non-optimal combination

由图4可知,其他组合的识别率有低于该组合识别率的情况,也有高于该组合识别率的情况,故该类组合为非优型组合。

2 特征参数集构建规则

特征参数集是特征组合(含单特征)中优型组合的一种,若记某特征参数集为Θ,所有特征参数组合构成的集合为Ω,则{Θ}为Ω的一个子集,即:{Θ}⊂Ω。所有特征参数集构成的集合Ψ,Ψ是对Ω的精简,即:Ψ⊆Ω,在识别率上Ψ和Ω是等效完备的。

根据第1.3节对优型组合的定义,优型组合的识别率高于对应特征的其他所有组合情况,同样,特征参数集的识别率应高于组成参数集对应特征的其他所有组合情况。设某特征参数集Θ={Θ1,Θ2,…,Θn},由对应特征Θ1、Θ2、…、Θn的其他组合构成的集合记为Λ,由Θ1、Θ2、…、Θn组成的特征参数集全集记为Ψ,则关于特征参数集Θ有以下结论成立:

(1)Θ的识别率高于Λ中所有元素的识别率，即

p(Θ)>p(κ|Λ)

(4)

式中,p(·)为识别率函数,κ为Λ中的元素。

(2)Θ为Ψ中含特征参数个数最多的集合,当θ为全特征参数集时,与Λ互为补集，即

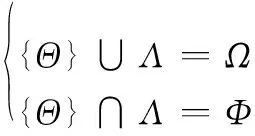
(5)

式中,Φ为空集。

(3) 当Θ为单特征参数集时,{Θ}=Ψ,Λ=Φ。

(4) 所有单特征构成的组合{Θ1},{Θ2},…,均为特征参数集。

(5) 对于特征个数分别为n、n+1的特征参数集Θn和Θn+1,若满足Θn⊂Θn+1,则称Θn和Θn+1为同源特征参数集。同源特征参数集的最大识别率是随特征个数递增的,即

max(p(Θn+1(Θ1,Θ2,…,Θn)))>

max(p(Θn(Θ1,Θ2,…,Θn)))

(6)

因此,对于从特征参数组合中找出所有的特征参数集,可根据其构建规则,按特征个数递增的步骤进行标记。

步骤1标记所有单特征组合为特征参数集;

步骤2对所有的两个特征组合,与对应的单特征组合进行比较,若某组合识别率均高于单特征,则标记该组合为特征参数集;

步骤3对所有的3个特征组合,与步骤1、步骤2中对应的特征参数集进行比较,若某组合识别率均高于已标记的对应特征参数集,则标记该组合为特征参数集;

步骤4后续个数的特征组合,可类似步骤3,与之前所有已标记的对应特征参数集进行比较,依次标记是否为特征参数集。

3 特征参数集时间成本分析

对于同源特征参数集,特征个数越多识别率越高,然而,高的识别率有可能耗费较高的时间成本。在RES识别中,由于SVM属于基于统计学习的分类器[25-28],其分类模型可提前通过学习训练获得,因此,参数集的时间成本主要由识别过程的2个环节产生,一是特征提取环节产生的特征提取时间,另一是分类识别环节产生的分类识别时间。

计算算法时间的常用方法有2种,一种是计算该算法中所有语句的频度之和[29],另一种是计算算法执行时用到的加减乘除等运算的次数[30-31]。这2种方法通过对算法的详细分析均能准确地定量计算出算法的时间,但是,随着算法开发平台和对应计算机语言的发展,大量使用各种算法包和隐性封装各种函数,使准确分析出算法的步骤变得十分困难。因此,本文采用工程应用中常用到的统计分析方法,来获取特征提取时间和分类识别时间。

3.1 特征提取时间

由于特征参数的提取时间和原始波形数据的长度有关,而原始波形数据的长度与信号采样率和脉冲宽度有关,对于未知信号,信号的脉冲宽度是不能事先获得的,所以,原始波形数据的长度也无法事先确定。但是,为便于统一决策参考,这里将原始波形数据的基准长度定义为2 048(采样频率为120 MHz时,脉宽范围为8.54～17.06 μs)。

分别根据特征提取算法,对随机产生的不同调制类型的原始波形数据做特征提取实验,记录每次实验耗费时间,如此进行200次蒙特卡罗实验,将实验时间均值作为特征提取时间。表1所示为各特征参数的提取时间,实验平台参数为:英特尔i3双核CPU,主频1.70 GHz,内存4.00 GB,Windows 8.1中文版64位操作系统。

表1 特征参数提取时间

3.2 分类识别时间

SVM在进行RES识别时,分类识别时间主要与样本的维数有关,在7种特征参数中,频谱特征、时频特征、双谱特征、模糊函数特征的维数为256维,记为一次变换特征,相像系数特征、熵值特征、复杂度特征的维数为2维,记为二次变换特征。由于一次变换特征与二次变化特征在维数上相差较大,多次仿真实验表明,当一次变换特征与二次变换特征组合时,二次变换特征的维数对分类识别时间的影响较小。0～4个一次变换特征及其分别与1～3个二次变换特征组合的分类识别时间如图5所示,图5中横坐标依次为1个二次变换特征的组合、2个二次变换特征的组合、3个二次变换特征的组合、1个一次变换特征的组合、1个一次变化特征与1个二次变换特征的组合、1个一次变化特征与2个二次变换特征的组合、……、2个一次变换特征的组合、2个一次变化特征与1个二次变换特征的组合、……、4个一次变化特征与3个二次变换特征的组合。

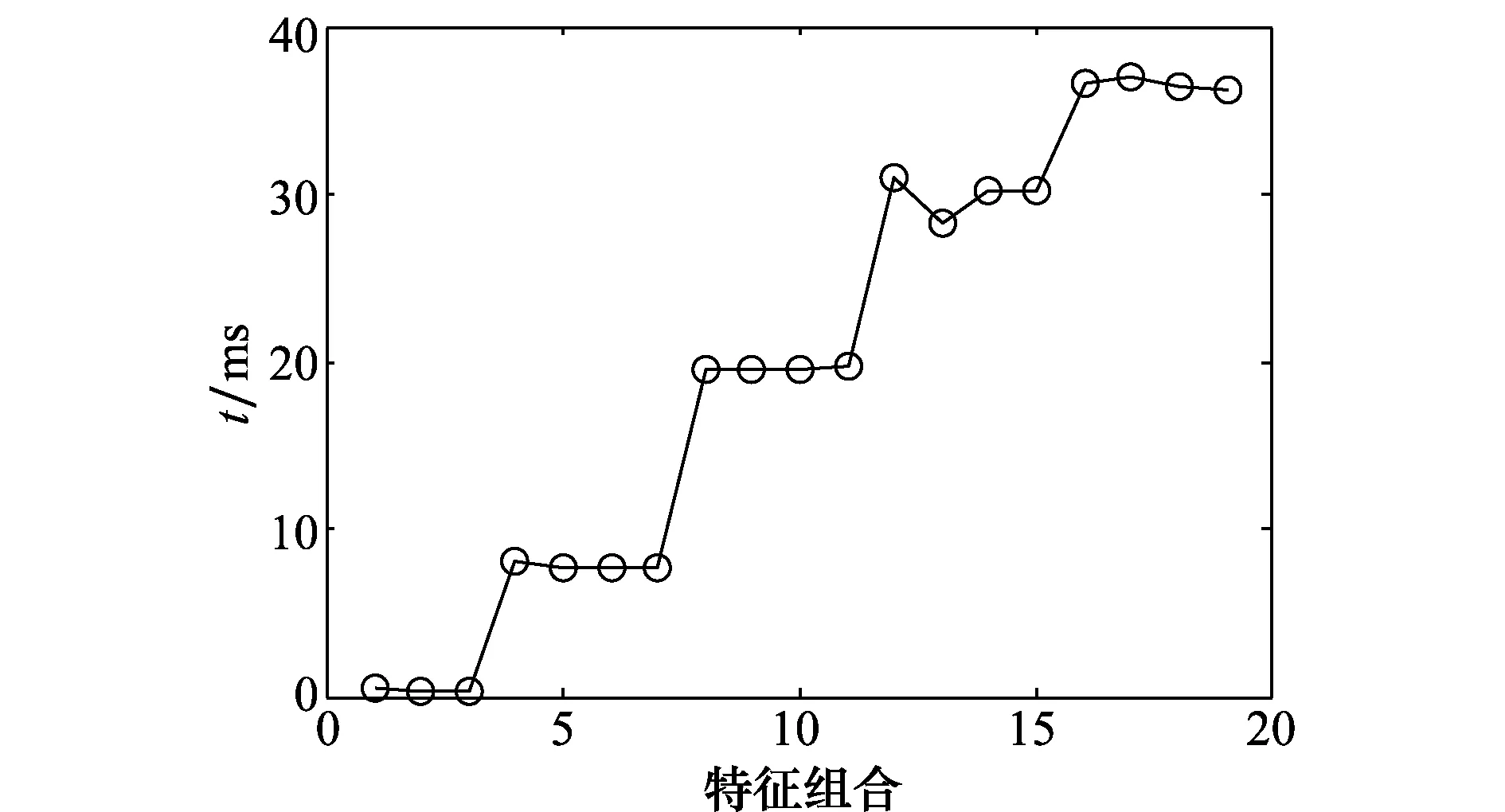
图5 特征组合分类识别时间图Fig.5 Time map of characteristic combination classification and recognition

由图5可知,特征组合分类识别时间随一次变换特征个数的增加呈阶梯状递增,因此,按照一次变换特征的个数,可将分类识别时间分为5个等级,分别对应0～4个一次变换特征及其与二次变换特征组合方式。通过多次蒙特卡罗实验,获得不同等级的分类识别时间如表2所示(实验平台参数同上)。

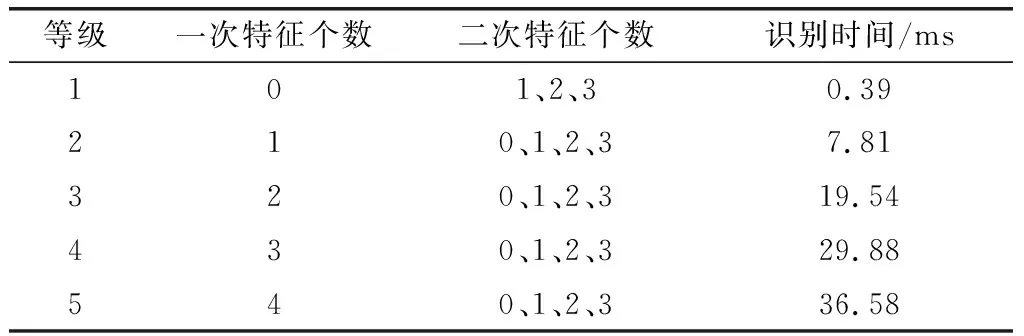
表2 特征组合分类识别时间

3.3 总时间成本

在RES识别中,特征提取环节和分类识别环节之间为串联关系。因此,特征参数集的总时间成本为特征提取时间和分类识别时间之和,即

T=Tc+Ts

(7)

式中,T为参数集的总时间成本；Tc为特征提取时间；Ts为分类识别时间。

(8)

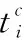
若Θ={Θ1,Θ2,…,Θn}中属于一次变换特征的个数为m,则参数集分类识别时间为

(9)

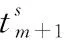
4 2种典型特征参数集的应用构建

根据上述特征参数集的构建规则和时间成本计算方法,得出7种特征的所有参数集的识别率和时间成本如表3所示,表中,fft、stft、bi、amb、cr、en、cp分别代表频谱特征、时频特征、双谱特征、模糊函数特征、相像系数特征、熵值特征、复杂度特征。

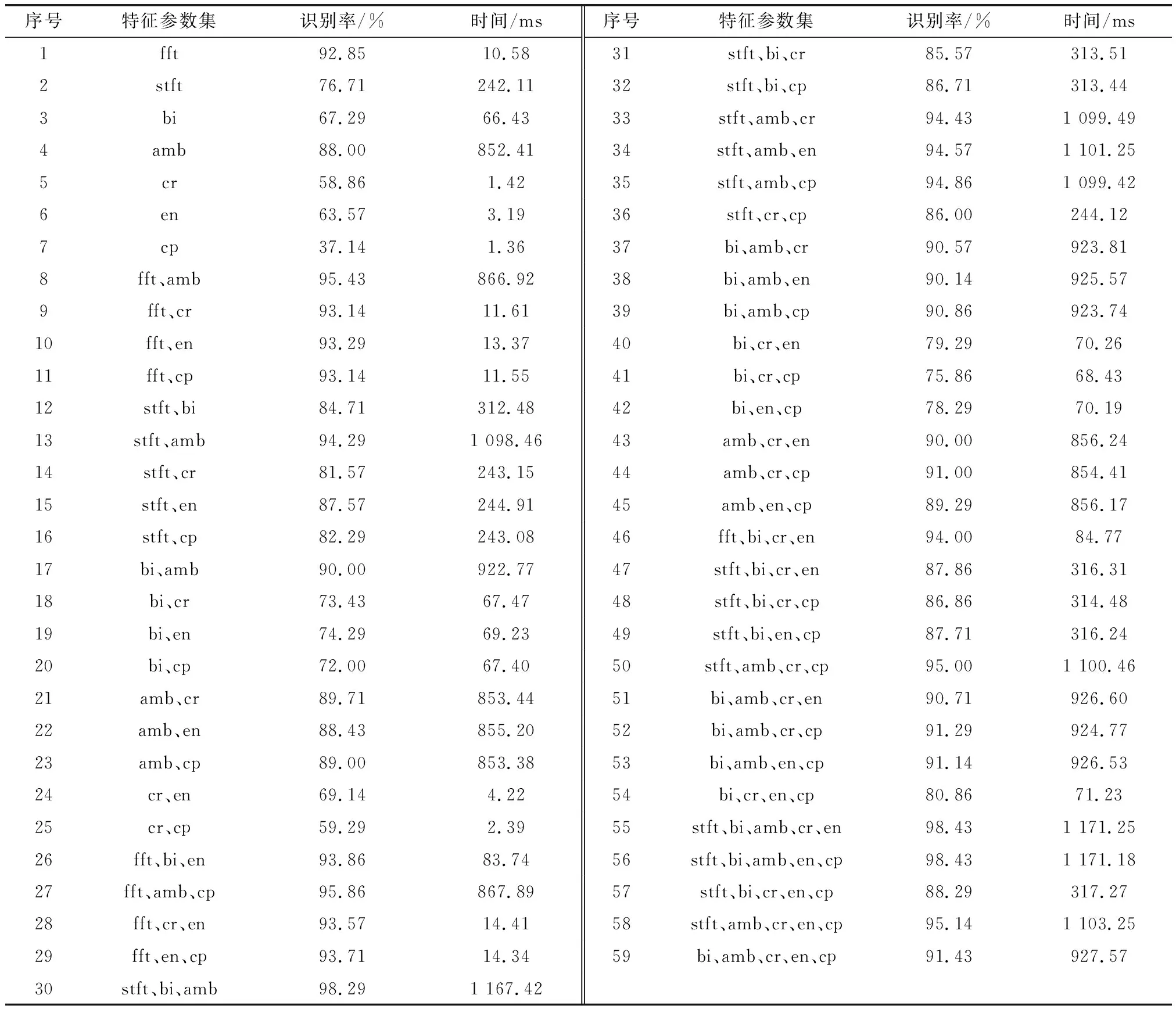
表3 特征参数集的识别率和时间成本

各特征参数集的对应识别率和时间成本数据按式(10)进行归一化。

(10)

式中,dmax、dmin分别为数据序列{d1,d2,…,dn}中的最大值和最小值。

归一化后的特征参数集识别率与时间成本之间的关系如图6所示。

由图6可知,特征参数集的识别率和时间成本之间并没有出现严格一致的变化关系,也就是说特征参数集特征组成情况与识别率、时间成本之间没有恒定的单调关系,因此,需要根据实际需求做出最优的决策——在获得较高识别率的同时消耗较小时间成本。

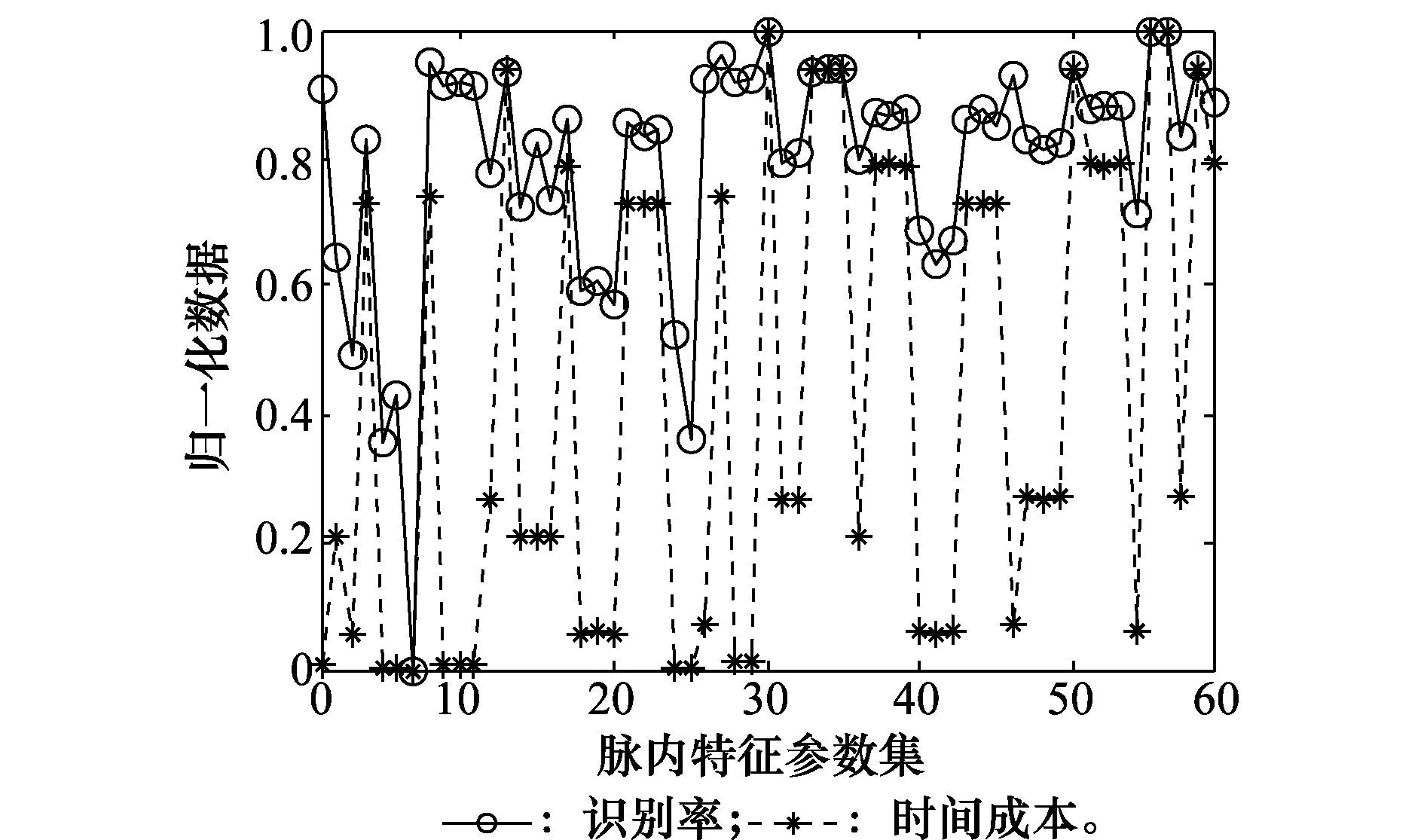
图6 特征参数集识别率与时间成本对应关系Fig.6 Relationship between recognition rate and time cost of characteristics parameters

在RES识别中,有2种情况是经常遇见的,一是现场采集波形数据,实时识别RES;二是采集存储波形数据,事后识别RES。对于第1种情况,最优决策是在限定识别率条件下,选择时间成本最小的特征参数集,该特征参数集定义为时效集;对于第2种情况,最优决策是在限定时间成本条件下,选择识别率最高的特征参数集,该特征参数集定义为精准集。

4.1 时效集

记特征参数集为Θ,所有特征参数集构成的集合为Ψ,则时效集为

ΘAE=

Θ|(Θ∈Ψ,min(T(Θ))|p(Θ)≥p0)

(11)

式中,T(Θ)为特征参数集的时间成本；p(Θ)为特征参数集的识别率；p0为限定识别率。

根据定义式(11),构建特征参数时效集的方法步骤如下:

步骤1将所有特征参数集的识别率表和时间成本表按特征参数集的构建方式进行对应合并整合;

步骤2找出所有识别率高于限定识别率的特征参数集;

步骤3找出步骤2中时间成本最小的特征参数集。

例如,某实时识别场合,给定最低识别率为85%,根据合并整合的特征参数集表(表3),筛选出特征参数集有序号1、4、8、9、10、……,上述特征参数集中,时间成本最小为10.58 ms,对应序号1,特征参数集构成为频谱特征,此即为满足需求的时效集。

4.2 精准集

记特征参数集为Θ,所有特征参数集构成的集合为Ψ,则精准集为

ΘCP=Θ|(Θ∈Ψ,max(p(Θ))|T(Θ)≤T0)

(12)

式中,p(Θ)为特征参数集的识别率；T(Θ)为特征参数集的时间成本；T0为限定时间成本。

根据定义式(12),构建特征参数精准集的方法步骤如下:

步骤1将所有特征参数集的识别率和时间成本按特征参数集的构成方式进行对应合并整合;

步骤2找出所有时间成本小于限定时间的特征参数集;

步骤3找出步骤2中识别率最高的特征参数集。

例如,某实时识别场合,给定最低每次识别时间在1 s以内,根据合并整合的特征参数集表(见表3),筛选出特征参数集有序号1、2、3、……、27、……,上述特征参数集中,识别率最高为95.86%,对应序号27,特征参数集构成为频谱特征、模糊函数特征、复杂度特征,此即为满足需求的精准集。

5 结 论

为突破单个脉内特征参数识别性能的“边缘效应”,获得更高的识别率,从特征参数的组合入手,提出特征组合的方式和相关约定,并重点研究了特征种类、特征个数、信号环境对特征组合识别性能的影响。在此基础上,进一步对特征组合中的优型组合进行研究讨论,提出特征参数集的构建规则和生成方法,并就特征参数集的时间成本进行了分析。最后,根据识别率和时间成本因素,构建了2种典型的特征参数集——时效集和精准集,为脉内特征参数集在RES监测、侦察、分析等工程应用方面奠定了良好的理论基础。