分段优化RRT的无人机动态航迹规划算法
2018-07-27李文广孙世宇李建增胡永江
李文广, 孙世宇, 李建增, 胡永江, 张 岩
(陆军工程大学石家庄校区无人机工程系, 河北 石家庄 050003)
0 引 言
目前,大多数的航迹规划主要研究在静态威胁下如何规划航迹[1-3],对于突发威胁下的动态航迹规划问题相关文献较少。在实战背景下,只考虑静态威胁对无人机飞行安全的影响是不符合实际任务要求的。无人机动态航迹规划就是解决无人机在发现突发威胁时,该如何重新规划局部航迹的问题。这有利于提升无人机对于复杂战场环境的适应能力和生存能力,同时更符合实战背景,所以研究无人机动态航迹规划意义重大。
在无人机动态航迹规划方面,学者们做了大量的工作:文献[4]提出了一种改进的快速扩展随机树(rapidly-exploring random tree, RRT)算法,提升了算法搜索路径的效率和可行性,路径的可跟踪性更强。但该算法只考虑了静态威胁下的航迹规划问题,不符合实战任务要求。文献[5]提出了稀疏A*和人工势场相结合的动态航迹规划算法。该算法首先利用稀疏A*算法完成全局航迹规划,然后在出现突发威胁的情况下结合人工势场法完成局部航迹规划。其充分利用了稀疏A*和人工势场法的优点,同时避免了出现局部极小的缺陷。但稀疏A*算法需要前期对规划空间进行预处理,算法效率不高,并且用稀疏A*算法的航迹代价函数去近似描述局部航迹的代价,误差较大。文献[6]提出了基于动态贝叶斯网络(dynamic Bayesian network, DBN)威胁评估模型与模型预测控制(model predictive control, MPC)路径规划算法相结合的方法。该算法首先利用DBN模型评估得到突发威胁的威胁等级,然后结合航迹规划算法规划动态航迹。其能够解决一般不确定的突发威胁以及尾随无人机的突发威胁的动态航迹规划问题。但考虑空中威胁(敌机)并不是实战条件下的主要威胁来源,实用性不强。文献[7]提出了一种基于动态步长的实时航迹规划算法,即无人机在飞行过程中实时规划飞行航迹,若出现突发威胁,则通过设置子目标点的方法,规划局部航迹。该算法将规划空间进行了简化处理,降低了问题的复杂度,同时提升了算法在威胁区域搜索航迹的精度。但由于整个规划过程都是实时的,对算法的实时性要求非常高,也对无人机的智能化程度要求非常高。
上述航迹规划算法都针对突发威胁下的动态航迹规划问题进行了不同算法的创新和改进,但仍存在以下问题:前期全局航迹规划效率较低,导致整体规划效率不高;DBN威胁评估模型对于突发威胁的等级评估结果可信度不高;算法对无人机智能化程度要求太高,实用性不强。
针对以上问题,本文提出了分段优化RRT的无人机动态航迹规划算法(dynamic path planning of unmanned aerial vehicle based on segment optimization RRT, DPPUAVSORRT)。该算法首先利用分段优化RRT算法生成全局航迹。然后在规划空间中若有对无人机飞行安全产生影响的突发威胁,则根据新的威胁信息确定局部航迹规划的起点和终点,并使用分段优化RRT算法生成从新起点能够绕过突发威胁并回到原航迹的局部航迹。若无,则继续沿着全局航迹飞行直至目标点。最后通过实验对所提出的方法进行了验证。
1 算法流程
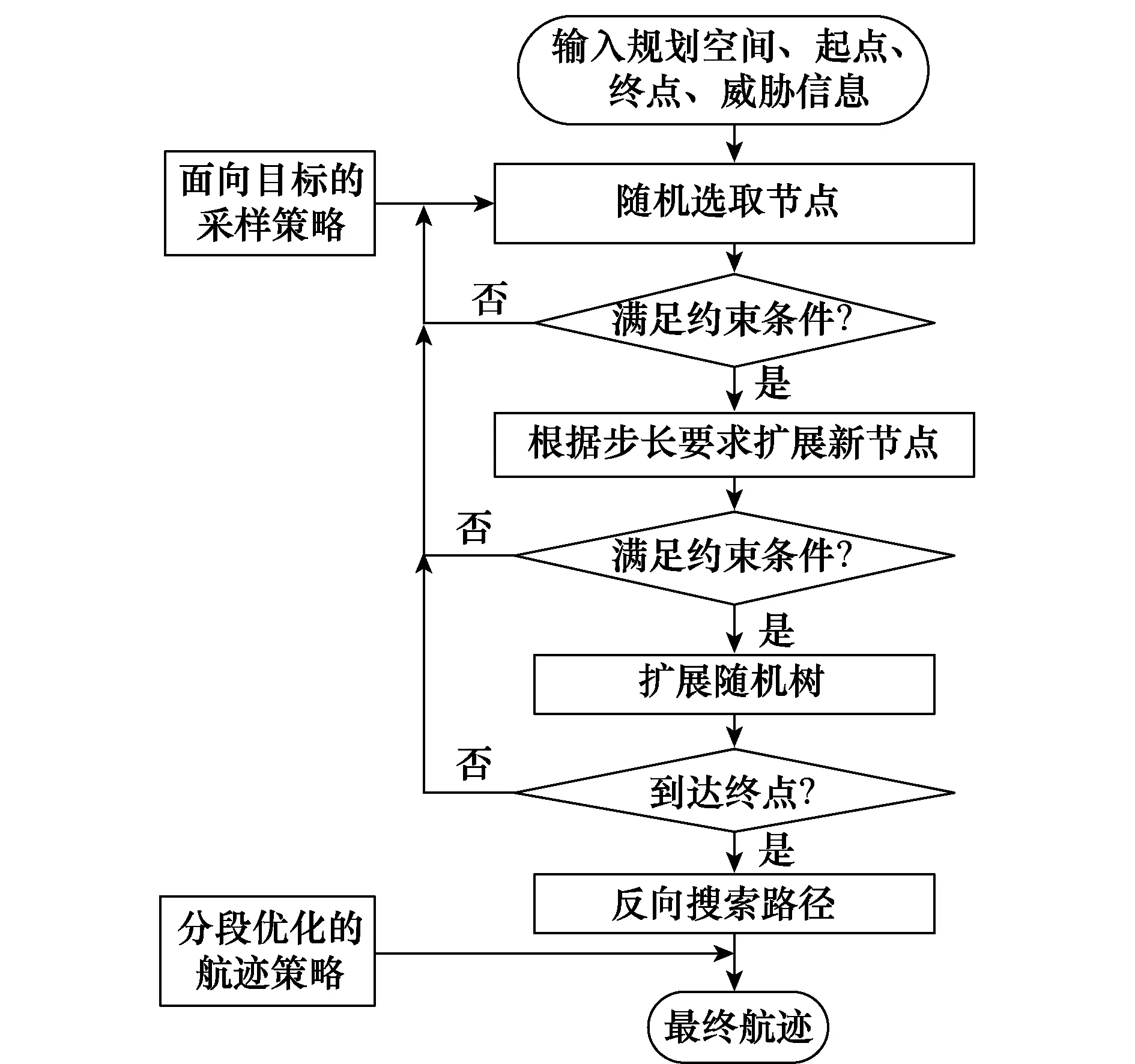
DPPUAVSORRT算法流程如图1所示。

图1 DPPUAVSORRT流程图Fig.1 Flowchart of DPPUAVSORRT
步骤1规划全局航迹。根据已知的战场情报信息和任务要求,利用分段优化RRT算法规划从起点到终点的全局航迹。
步骤2威胁实时检测。无人机沿着全局航迹飞行时,利用各类传感器实时探测战场信息,同时不间断接收地面的情报信息。判断规划空间中是否有未知突发威胁产生,且突发威胁的位置、类型和作用范围是否对无人机的飞行安全有很大影响。
步骤3更新规划空间。根据步骤2的结果,若有突发威胁,则更新整个规划空间的威胁信息,包括威胁的位置、类型和作用范围等(将威胁作用范围放大1.2倍);若无,则无人机继续沿着全局航迹飞行,并继续探测战场信息。
步骤4确定新的起点。动态航迹规划算法首先根据突发威胁的相关威胁信息,判断所有航程点中最先可能处在威胁作用范围内的航程点pj和最后可能处在威胁作用范围内的航程点pk(2 步骤5规划避让航迹。根据步骤4确定的起点和终点,利用分段优化RRT算法搜索得到避让突发威胁的局部航迹,使得无人机能够成功绕过突发威胁并回到原航迹。 相关说明: (1) 假定全局航迹的前两个航程点和最后两个航程点之内不会有未知的突发威胁。 (2) 将威胁作用范围扩大1.2倍,是为了在规划局部航迹时,降低航迹的威胁代价以及无人机被击落的概率。 (3) 利用分段优化RRT算法规划得到的航迹经过B样条曲线法平滑后是大量拟合航迹的点,通过对这些拟合点的处理,设置均匀分布的若干航程点,可确保设置的起点pj-2和终点pk+2不会距离突发威胁太近,提高规划的成功率。 分段优化RRT算法流程如图2所示。 图2 分段优化RRT算法流程图Fig.2 Flowchart of segmented optimization RRT 步骤1搜索节点。在整个规划空间中根据面向目标的采样策略随机选取节点。 步骤2节点筛选。根据步骤1选取的节点,判断其是否满足所有约束条件。若满足,则执行步骤3;若不满足,则执行步骤1。 步骤3扩展随机树。在随机树中找到离节点最近的叶节点,并根据步长要求扩展新的节点(该节点也必须满足所有约束条件),将新的节点加入到随机树中。若不存在,则执行步骤1。 步骤4反向搜索。当随机树扩展到终点或距离终点在一个步长以内时,反向搜索随机树,找到起点和终点之间的最短航迹。 步骤5分段优化。根据分段优化的航迹策略对所有航程点进行处理,分段优化航迹。 传统RRT算法在扩展随机树时,是对整个规划空间进行随机采样并得到随机节点prand,这样虽然有利于对未知的规划空间进行探索,保证了树节点在规划空间中的均匀分布,但实际上在规划空间中的部分区域扩展随机树对寻找路径没有实质性的帮助,反而导致了随机树扩展效率低,搜索路径速度慢的缺点。 面向目标的采样策略是通过设定引导因子来改变随机节点的采样规则。引导因子是将终点pend以一定的概率q(引导因子的大小就是q值的大小)作为随机节点prand(prand=pend),导致随机节点的选取并不完全是随机的。这样使得随机树扩展时向目标位置生长的趋势更加明显,减约了随机树在部分规划空间的扩展过程,大大减少了随机树扩展过程中随机节点的数目,不仅使搜索路径更具有目的性,而且有利于随机树快速扩展至目标点。 现有的大部分RRT改进算法都考虑了规划后的航迹是否满足无人机最小转弯半径等无人机自身性能的约束[1,4,8],于是对随机节点prand的选取提出了不同的约束条件,确保规划得到的航迹能够满足无人机的性能约束。但这一方面限制了算法对于各类无人机的通用性,另一方面增加了随机树扩展过程中的运算代价,对算法搜索路径的效率产生一定影响。 分段优化的航迹策略是将数据结构中“二分查找法”[9]的思想引入到RRT算法中。首先利用基于面向目标的采样策略RRT算法规划得到一系列航程点(按飞行顺序排列),接着利用二分法将所有航程点一分为二,并从后一半航程点中找到能与目标点pend直接相连且与所有障碍不相交的航程点,记为Pn-1(记pend=Pn),然后对起始点pstart和Pn-1之间的航程点再进行分段优化处理,得到Pn-2,重复以上步骤直到所有航程点处理完毕。 分段优化的航迹策略处理的航程点数量远远小于随机节点的数量,所以该优化策略的计算量远小于对随机节点的选取考虑无人机性能时的计算量,同时由于该改进策略不需要结合无人机的具体性能约束,使得算法通用性不受限制,并且该优化策略能够大大缩短路径长度。 相关性说明:分段优化的航迹策略不仅仅采用“二分法”,也可根据算法效率和精度的要求,对基于面向目标的采样策略RRT算法规划得到一系列航程点(按飞行顺序排列)多划分几段进行优化。 采用分段优化RRT规划得到的航迹是由几条线段组成的,但部分线段相交的拐点部分不够平滑,不利于无人机在拐点处的机动飞行,需进行平滑处理。 由于B样条曲线法兼备了Bezier曲线法的几何不变性、仿射不变性等优点,同时克服了由于整体表示带来不具备局部性质的缺点[10],使其在航迹规划中应用广泛。本文利用B样条曲线法对拐点部分路径点进行拟合,生成平滑路径。 B样条曲线方程可写为 (1) 式中,控制顶点为di(i=0,1,…,n);k次规范B样条基函数为Ni,k(u)(i=0,1,…,n),最高次数为k。基函数是由一个称为节点矢量的非递减参数u的序列U:u0≤u1≤…≤un+k+1所决定的k次分段多项式。 B样条的基函数采用Cox-deBoor递推公式,即 (2) 式中,i为节点序号;k是基函数的次数,共有n+1个控制点。 传统RRT算法的随机节点选取是在整个规划空间中随机选取的,使其能够对规划空间的未知区域展开搜索。而待扩展节点的概率是收敛于均匀分布的[11-14],算法具备概率完备性。本文引入面向目标的采样策略影响了算法随机节点选取的规则,下面从理论上对引入面向目标的采样策略RRT算法的概率完备性进行证明。 假设Dk(p*)表示节点p*与随机树上最近节点之间距离的随机变量。dk表示该随机变量的取值,k表示节点数,ε表示扩展步长。 定理1在n维有界规划空间U中(包含威胁),起始点pstart和目标点pend在同一连通区域内,当引入面向目标的采样策略RRT算法的随机树节点数趋向于无穷大时,扩展节点pi等价于目标点pend的概率为1。即 (3) 式中,Ufree表示安全子空间,即规划空间中无威胁障碍的区域。 证明设p*为Ufree中的任意一点,O(p*)表示以p*为圆心,ε为半径的圆形区域,则有 O(p*)={p‖p-p*‖≤ε} (4) O′(p*)表示O(p*)与Ufree的交集,则有O′(p*)=O(p*)∩Ufree,μ(O′(p*))>0,μ表示集合的测度。 初始i=1时,d1(p*)=ρ(pend,p*),其中ρ(pend,p*)表示p*与起始点的距离。当随机树不断扩展,随机节点prand位于O′(p*)内的概率满足 P{prand∈O′(p*)}>0 (5) 假设所有节点均在O′(p*)的外部,算法进一步扩展。当prand=p*时,依据pnew的扩展方法可知,Dk+1(p*)的数学期望是 E[Dk+1(p*)|prand=p*] (6) 当prand≠p*时,有 E[Dk+1(p*)|prand≠p*]≤E[Dk(p*)] (7) 进一步可得到 E[Dk+1(p*)]=E[qr·(Dk+1(p*)|prand=p*)+ (1-qr)·(Dk+1(p*)|prand≠p*)] (8) 式中,0 由此可以得出,引入面向目标的采样策略RRT算法在扩展过程中使得p*与随机树节点之间的距离在逐渐缩小,当且仅当随机树节点数趋于无穷大时,节点位于O′(p*)的概率为1,即 由此可知,引入面向目标的采样策略实质上只是改变了Ufree区域的大小,并没有改变传统RRT算法有界连通性以及随机采样性,保证了算法的概率完备性。同时在扩展节点趋于无穷时,保证扩展节点仍然服从于随机节点采样分布。 证毕 下面对引入面向目标的采样策略RRT算法的收敛性进行证明。 证明设X和Xi分别是传统RRT算法和引入面向目标的采样策略RRT算法的节点概率分布密度函数,且pstart和p*位于同一连通区域内,则存在一个序列p1,p2,p3,…,pn以及对应的O(p1),O(p2),…,O(pn)圆形区域,且满足pstart∈O(p1),p*∈O(pn),则有 Oi(pi)∩Oi+1(pi+1)≠∅,i=1,2,…,n-1 (9) (10) 设第i次扩展时Ufree中未被引入面向目标的采样策略RRT算法搜索到的区域为 Yi={p*∈Ufree|ρ(p*,q)>ε,∀ζ∈Hi} (11) ρ(p*,q)为p*与随机树节点q之间的距离,Hi为此时的节点集合,μ(Yi)为Yi的测度,且有Yi+1⊆Yi,当i→∞时,μ(Yi)→0。根据概率函数的光滑性,可知Xi概率收敛于X。 由上述证明可知,引入面向目标的采样策略RRT算法仍然是收敛的。 证毕 工作站配置:Thinkstation D30,CPU:Intel Xeon E5-2620 (双处理器),64G内存,64位Win7系统。 编程工具:Matlab 2015(64位)。 3.1.1 数据集 实验设置200×200的二维无量纲规划空间,起点为(10, 10),终点为(190, 190),用红色五角星表示。其中分别设有8个威胁区域,10个威胁区域和12个威胁区域,用黄色圆形区域表示。3种规划空间如图3所示。 图3 3种规划空间Fig.3 Three types of planning space 3.1.2 实验对象及相关参数设置 对象1分段优化RRT算法是以一定的引导因子q选取目标点pend作为prand。实验对q值在[0,1)(q=1时,无法成功规划航迹)范围内,每隔0.1取值,并进行仿真实验(步长设置为ε=5)。记录每个q值下的100次仿真数据。 对象2随机树扩展时,若随机节点prand和pnear(随机树上离prand最近的节点)之间的距离大于一个步长,则在pnear沿着prand的方向上,扩展一个步长ε得到新的节点pnew;若不大于,则直接将prand作为pnew。实验对步长ε值取1,3,5,8,10,12,15,20,25,30,35,40,45,50(引导因子q=0.5)。记录每个ε值下的100次仿真数据。 3.1.3 评估准则 指标1随机树节点数。随机树节点数是指在完成路径搜索时,扩展随机树的节点数。随机树节点数越少表征算法搜索路径时采样点越少,算法效率越高。 指标2路径代价。路径代价是指航迹规划算法计算得到路径的长度,这是航迹规划所关心的一项重要指标。因为在无人机性能有限的条件下,路径代价直接决定着规划的航迹是否可行。 指标3算法运行时间。算法运行时间是指在相同的硬件条件下算法的运行速度。在完成相同目标时,算法运行时间和算法效率呈负相关。 3.1.4 实验结果及分析 q值对算法性能影响的实验对比结果如图4所示。 图4 q值对算法性能的影响Fig.4 Effect of q value on the performance of the algorithm 将实验结果分析如下: (1) 由图4可知,整体上当q=0(等价于传统RRT算法)时,随机树节点数和算法运行时间都远大于其他情况,路径代价也大于其他情况,表明引入面向目标的采样策略RRT算法效率优于传统的RRT算法。 (2) 在第一种规划空间中,随机树节点数呈现递减趋势,但当q>0.5时,递减趋势很小,此时增大q值对随机树节点数的影响很小。路径代价随着q值的增大呈递减趋势。而算法运行时间在0.1 (3) 在第二种规划空间中,随机树节点数和路径代价的变化趋势与第一种规划空间相似。而算法运行时间在q>0.5时的增长趋势相对于第一种规划空间更加明显。但算法运行效率均低于第一种规划空间。 (4) 在第三种规划空间中,随机树节点数和路径代价的变化趋势与前两种规划空间相似。特别的是算法运行时间的变化趋势在q≥0.5时增长更快更明显。算法运行效率均低于前两种规划空间。 以上结果表明,增大q值能够有效降低算法的随机树节点数、路径代价以及在一定范围内降低算法运行时间。但较大的q值反而会降低算法运行效率,这是由于较大的q值使得随机节点prand以较大的概率选取目标点,导致随机节点的选取比较单一,不利于随机树的扩展。同时越复杂的规划空间,搜索路径的效率也比较低。 ε值对算法性能影响的实验对比结果如图5所示。 图5 ε值对算法性能的影响Fig.5 Effect of ε value on the performance of the algorithm 图5(a)步长为1时的随机树节点数(3种规划空间)远大于其他情况,为了实验数据显示更加客观形象,所以未在折线图中表示。图5(c)步长为1时的算法运行时间(规划空间2和规划空间3)远大于其他情况,也未在折线图中表示。 将实验结果分析如下: (1) 由图5可知,随着ε的增大,随机树节点数呈现递减趋势。路径代价开始在一定范围内波动,之后随着ε继续增大,呈现递增趋势。而算法运行时间也在一定范围内呈现递减趋势,过大的ε值反而会增大算法运行时间。整体上看在适当范围内选择ε的值能够有效降低算法运行效率。 (2) 在第一种规划空间中,随机树节点数呈现递减趋势,但当ε>25时,递减趋势很小,此时增大ε值对随机树节点数的影响很小。路径代价开始在一定范围内波动(ε为3时规划空间1的实验数据误差较大),之后随着ε增大,呈现递增趋势。而算法运行时间在5<ε≤35时变化很小,此时算法已经能够很快搜索得到路径。但当ε>35时,算法运行时间有增长的趋势,此时增大ε值反而降低了搜索路径的效率。 (3) 在第二种规划空间中,随机树节点数、路径代价以及算法运行时间的变化趋势与第一种规划空间相似。但算法运行效率均低于第一种规划空间。 (4) 在第三种规划空间中,3类性能指标的变化趋势同前二种规划空间。算法运行效率也均低于前两种规划空间。但路径代价在ε>30时增长趋势更快更明显。算法运行效率均低于前两种规划空间。 以上结果表明,在一定范围内增大ε值能够有效降低算法的运行效率。但较大的ε值反而会提升算法路径代价以及运行时间,大大降低算法运行效率。这是由于较大的步长虽然有利于减少随机树的扩展,简约了随机树扩展的空间。但是随着规划空间的复杂度提升,较大的步长使得扩展节点的失败率也在增大,只能通过更远距离的绕行来避开威胁,反而增大了路径代价和算法运行时间。 综上所述,引导因子q和步长ε的值在一定范围内能够提高算法搜索路径的效率,其取值不仅要考虑规划空间的复杂度也应结合具体任务要求、威胁态势和其他情报信息等条件。 3.2.1 实验对象及相关参数设置 实验对象:在设置的规划空间中,利用分段优化RRT算法计算得到起点和终点之间的路径。 仿真参数设置如表1所示。 表1 仿真参数设置 3.2.2 实验结果及分析 分段优化RRT算法实验结果如图6所示。 图6 分段优化RRT算法实验结果Fig.6 Simulation results of segmented optimization RRT 图6(a)、图6(b)中蓝色表示扩展的随机树,红色表示搜索得到的路径。图6(c)蓝色表示采用分段优化的航迹策略优化后的路径,红色表示B样条曲线法平滑后的路径。表2是对航迹进行分段优化前后的路径长度实验对比数据。 表2 分段优化前后路程比较 将实验结果分析如下: (1) 图6(a)的随机树扩展遍布整个规划空间,图6(b)的随机树扩展只分布在路径沿线的局部区域,表明引入面向目标的采样策略的RRT算法在扩展随机树的过程中大大节约了扩展空间,使得随机树向目标点扩展趋势更加明显,提升了算法搜索路径的效率。 (2) 图6(c)蓝色路径是分段优化RRT算法搜索得到的路径,由几条线段组成,相比于传统RRT算法大大减少了无人机进行机动转弯的部分。同时,由表2可知,分段优化RRT算法相对于传统RRT算法缩短了11.53%左右的路径长度。表明引入分段优化的航迹策略一方面能够减少无人机的机动转弯,算法的通用性更强;另一方面能够缩短路程长度,降低路径代价。 数据集以及相关参数设置均同第3.2节。动态航迹规划实验结果如图7所示。 图7 动态航迹规划实验结果Fig.7 Simulation results of dynamic path planning 图7中绿色圆点表示航程点,红色圆形表示突发威胁区域,绿色五角星表示动态规划航迹的起点和终点,淡蓝色表示局部航迹规划搜索得到的路径,紫色表示分段优化后的路径。 将实验结果分析如下: (1) 图7(a)是突发威胁所处的位置、范围对无人机沿着全局航迹飞行没有影响的情况下,无人机无需重新规划局部航迹,仍沿着全局航迹飞行即可。 (2) 图7(b)是突发威胁的作用范围与全局航迹相交时,无人机需规划局部航迹的情形。此时算法能够生成避让突发威胁的局部航迹,并重新回到原航迹。 (3) 图7(c)与图7(b)相似,区别在于图7(c)在突发威胁的两侧存在两个狭窄通道,只有通过上方的通道绕行才能避开突发威胁。而算法能够根据威胁信息在可行的通道内规划局部航迹,确保无人机能够安全避让突发威胁。 (4) 实验表明算法能够准确判断突发威胁的位置和范围是否会对无人机的飞行安全产生影响,若有影响,则算法能够成功规划得到新起点和终点间的路径并回到原航迹。 本文提出分段优化RRT的无人机动态航迹规划算法,并通过实验验证了算法的可行性与优势,主要得到以下结论: (1) 面向目标的采样策略能大大简约随机树在规划空间的扩展,提升算法搜索路径的效率。 (2) 分段优化的航迹策略使得算法的通用性更强,同时减小了路径代价,使得整体航迹代价更小,实用性更强。 (3) DPPUAVSORRT能够准确判断突发威胁对于无人机的飞行安全是否有影响。若有,则规划局部航迹,确保无人机能够安全避让突发威胁。若无,则无人机继续沿着全局航迹飞行。2 分段优化RRT算法
2.1 算法流程
2.2 面向目标的采样策略
2.3 分段优化的航迹策略
2.4 航迹平滑
2.5 算法的概率完备性及收敛性证明
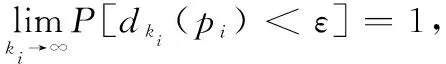
3 实验验证
3.1 分段优化RRT算法参数设置实验



3.2 分段优化RRT算法实验

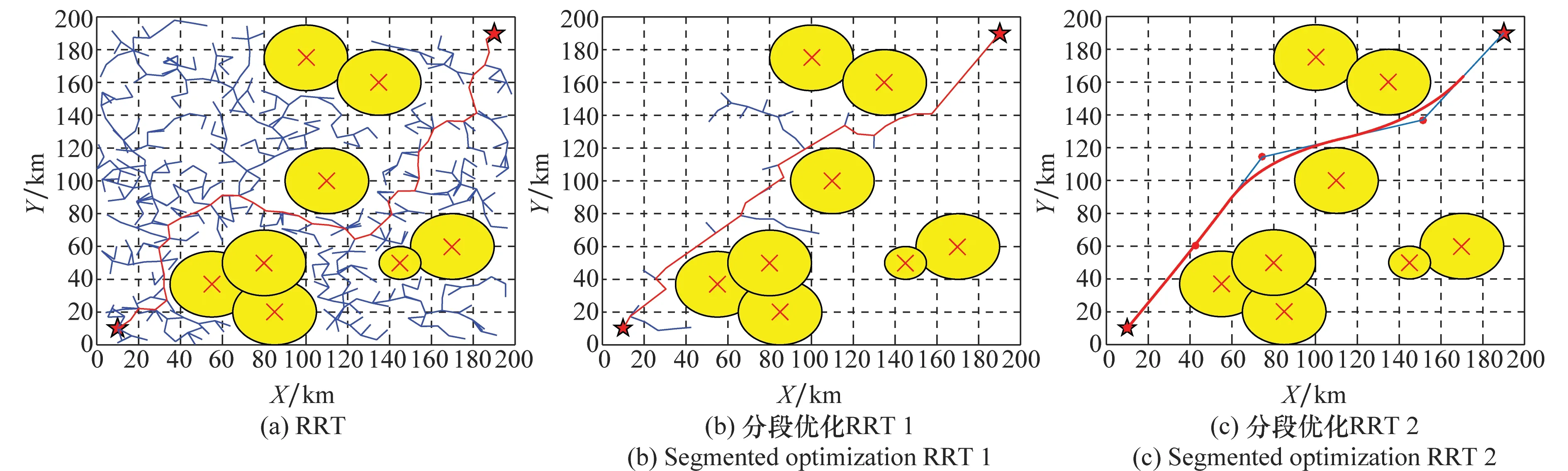

3.3 动态航迹规划实验

4 结 论
