基于极化单脉冲雷达的角度估计方法

刘业民, 邢世其, 李永祯, 孙 豆, 王雪松,2

(1. 国防科技大学电子信息系统复杂电磁环境效应国家重点实验室, 湖南 长沙 410073;2. 国防科技大学研究生院, 湖南 长沙 410073)

0 引 言

雷达主动寻的方式因其全天时、全天候、作用距离远等优点而备受精确制导武器青睐,其在末制导跟踪过程中,通常采用单脉冲技术来实现目标角度测量。利用箔条形成质心干扰是舰艇对抗精确制导武器的有效方法[1],当存在质心干扰时,若继续采用传统的单脉冲技术测量目标角度,通常会产生较大的角误差,最终导致精确制导武器偏离打击目标[1]。因此,如何有效地对抗箔条质心干扰,是提高精确制导武器作战效能的根本所在,具有非常重要的军事意义。

关于如何对抗箔条质心干扰的问题,梳理目前公开的文献报道,大概归纳为4种思路:第1种思路是箔条质心干扰检测[2],这是抗箔条质心干扰的前提和基础;第2种思路是先抑制干扰,再直接用传统的和差通道单脉冲比估计目标的角度[2-4],该思路在抑制干扰时需要目标或者干扰的极化描述子先验信息;第3种思路是用极化对比等方法增强目标信号的同时抑制干扰,再用常规和差通道单脉冲比来估计目标的角度[5],该思路通常同时需要目标和干扰的极化描述子先验信息;第4种思路是在不抑制箔条干扰的情况下,通过信号处理的方法直接估计目标和干扰的角度,这种思路的核心思想是把抗箔条质心干扰的本质看作是不可分辨的两个目标的角度估计问题。目前,国内外对单脉冲测角雷达不可分辨的两(多)个目标角度估计的研究较深入。文献[6]使用两个连续的脉冲数来计算同分辨单元内两个非起伏目标的角度;文献[7]通过一种巧妙的建模方法,得到了文献[6]的解析解,这种方法必须满足Sherman条件,即在两个脉冲回波中,两个目标的回波必须具有相同的幅值比与不同的相位差,这种方法对脉间是快起伏的目标往往难以奏效;文献[8]提出了一种基于单脉冲比的统计特性来估计两个不可分辨的瑞利起伏目标的角度,该方法需要知道两目标的雷达散射截面(radar cross section,RCS)比值;文献[9]提出了用最大似然(maximum likelihood,ML)法来估计两个不可分辨目标的角度,在此基础上,文献[10]发现了最大似然法计的闭合解,相比于文献[9],大大降低了计算复杂度,不足之处是文献[9-10]均需预先知道两个目标的RCS;此外文献[6-10]所提的角度估计方法都是针对相同类型的两(多)个目标,而对于箔条质心干扰,目标与干扰属于不同类型。文献[11]提出了一种利用极化单脉冲雷达抗质心干扰的方法,但该方法需要预先知道箔条的极化比信息。在实际应用中,由于两(多)个目标是不可分辨,通常情况下难以获取其RCS(或RCS的比值)、干扰的极化比等先验信息。为此,文献[12]提出一种基于单脉冲测角系统中“差-差”通道信息,结合正常和、方位差、俯仰差通道信息,由于“差-差”通道信号表征了两个目标方位差信号与俯仰差信号的耦合量,因此可以通过求解包含4个复等式的方程组来解算两个不可分辨目标的角度,随后,一些学者对四通道解算两个不可分辨目标的方法展开研究[13-14]。值得指出的是,当两目标在俯仰角上接近时,该方法解算出的两目标方位角角度值会存在很大的方差[12],而在质心干扰中,目标和箔条在俯仰角上通常情况下是很接近,差别主要体现在方位角上[3]。因此,该方法在质心干扰场合中受到一定程度上的应用限制。

基于上述背景和问题,本文以传统单脉冲测角系统为对象,在文献[15]提出的双极化单脉冲雷达系统和差信号模型的启发下,提出了一种基于极化单脉冲雷达的角度估计方法,该方法由传统单脉冲雷达系统的单极化天线改为采用双极化天线,目前公开报道双极化天线已应用于雷达导引头[16],因而不会因平台空间问题而限制其应用。本文所提方法具有以下几个优点:①相比于文献[7-11]所提方法,本文方法无需预先知道两目标的RCS(或RCS的比值)、干扰的极化比等先验信息;②相比于文献[9]的ML估计方法,本文方法计算复杂度小,有利于实时估计目标的角度;③本文所提方法既可用于估计两个不同类型目标的角度,也可用于估计两个相同类型目标的角度,适用范围宽。论文共分4部分:首先阐述了一种双极化和差信号模型;接着分析了在箔条质心干扰条件下雷达接收机输出信号的概率分布;然后在双极化和差信号模型、目标和干扰输出信号特征的基础上,提出了一种基于极化单脉冲雷达估计目标角度的方法,并给出了估计目标角度的流程图;最后对本文所提方法进行了仿真实验,并与其他文献方法进行了估计性能对比。

1 双极化和差信号模型

图1给出了双极化单脉冲雷达系统和差信号模型,与传统典型的单脉冲雷达系统相比,本文所阐述的模型中每个子波束的天线馈电单元由传统的单极化天线改为采用双极化天线。为了保证目标在交叉极化通道中有足够的信噪比,定义雷达正交极化基为线性旋转基(a,a⊥),其中,a代表45°线极化,a⊥代表-45°线极化[17],并假定天线馈电单元合成发射45°线极化波,每个子波束的天线馈电单元同时接收45°线极化波和-45°线极化波。进一步假设A、B、C与D表示对应子波束接收到的复回波信号,则双极化系统两种极化6路和、方位差(azimuth, Az)与俯仰差(elevation, El)通道接收信号可以表示为

sa=Aa+Ba+Ca+Da

(1)

sa⊥=Aa⊥+Ba⊥+Ca⊥+Da⊥

(2)

daAz=(Ca+Da)-(Aa+Ba)

(3)

da⊥Az=(Ca⊥+Da⊥)-(Aa⊥+Ba⊥)

(4)

daEl=(Aa+Ca)-(Ba+Da)

(5)

da⊥El=(Aa⊥+Ca⊥)-(Ba⊥+Da⊥)

(6)

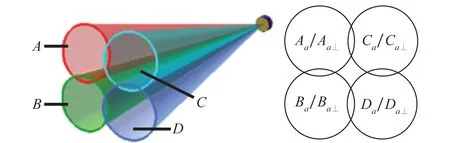
图1 双极化单脉冲雷达系统和差信号模型Fig.1 Signal model of the sum and difference channels based on dual polarization monopulse radar system

单脉冲雷达导引头利用4个子波束来估计目标水平和俯仰角。当存在箔条质心干扰时,目标与箔条干扰处于同一距离分辨单元,目标和干扰的俯仰角是基本相同,角度差异主要体现在方位向。因此,在下面的章节里,主要讨论一维角度域,即只分析目标方位角。值得指出的是,本文提出的估计目标方位角的算法与俯仰向处理结果具有相似性。

2 箔条质心干扰条件下雷达接收机输出信号概率分布

当箔条质心干扰存在时,则一个距离和角度分辨单元里同时包含目标和干扰信号,那么单脉冲测角系统和差通道中所接收到的回波信号可表示为

sa,p=xaa,p+yaa,p+nsa,p

(7)

sa⊥,p=xa⊥a,p+ya⊥a,p+nsa⊥,p

(8)

daAz,p=κaθ1xaa,p+κaθ2yaa,p+nda,p

(9)

da⊥Az,p=κa⊥θ1xa⊥a,p+κa⊥θ2ya⊥a,p+nda⊥,p

(10)

式中,s代表和通道;d代表差通道;下标p∈{I,Q},当p=I或p=Q分别表示和、差通道中回波信号的实部或虚部;xaa,p和xa⊥a,p分别表示共极化(aa)和交叉极化(a⊥a)通道中目标的回波信号;yaa,p和ya⊥a,p分别表示共极化和交叉极化通道中箔条的回波信号;θ1和θ2分别表示目标和干扰的偏轴角,即目标和干扰在单脉冲测角系统的角度信息;κa和κa⊥分别表示共极化和交叉极化通道的单脉冲斜率,在天线设计阶段,该参数先验可知;nsa,p、nsa⊥,p、nda,p和nda⊥,p分别为和差通道的热噪声和杂波信号。

在反舰应用场合中,假设共极化通道中舰船目标的RCS服从斯威林IV起伏模型[3],且交叉极化通道中舰船目标的RCS也服从斯威林IV起伏模型[15]。那么共极化和交叉极化通道中舰船信号回波的概率分布函数(probability density function,PDF)可分别表示为

(11)

(12)

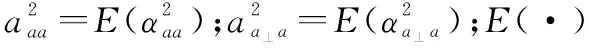
(13)

(14)

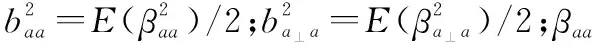
(15)

(16)

(17)

(18)

式中,Var[·]表示求方差操作符,在本文中假设各路通道中的热噪声和杂波的方差是已知的,在大多数情况下,目前单脉冲测角系统都能够对其很好地估计[10]。

3 估计目标角度及流程

根据文献[2-3,8],本文提出的信号模型假设也满足以下几个条件:①回波信号的实部和虚部彼此相互独立;②若采用频率分集技术[8],则同一通道中不同脉冲间的回波信号相互独立;③同一或不同和差通道中,舰船回波信号、箔条干扰回波信号与噪声之间相互独立。为此,不难求得和差通道中所接收到回波信号的二阶统计量分别为

(19)

(20)

(21)

(22)

(23)

(24)

另一方面,和差通道中所接收到的回波信号的二阶统计量可通过回波原始数据被估计出来,即

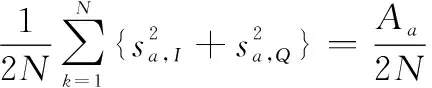
(25)

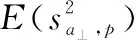
(26)

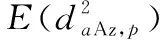
(27)

(28)

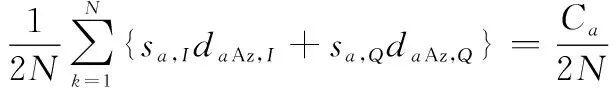
(29)

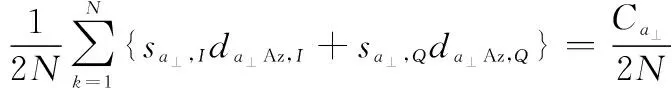
(30)

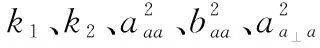
(31)

式中,中间变量定义为

(32)

(33)

(34)

(35)

(36)

(37)

(38)

(39)

(40)

(41)

综上所述,估计目标角度算法流程如图2所示。此外,从式(31)可以看出,求解舰船目标角度有两个值,选择哪个值,取决于舰船目标和箔条干扰角度的相对大小,当θ1>θ2时,可以确定舰船目标的估计偏轴角为

(42)

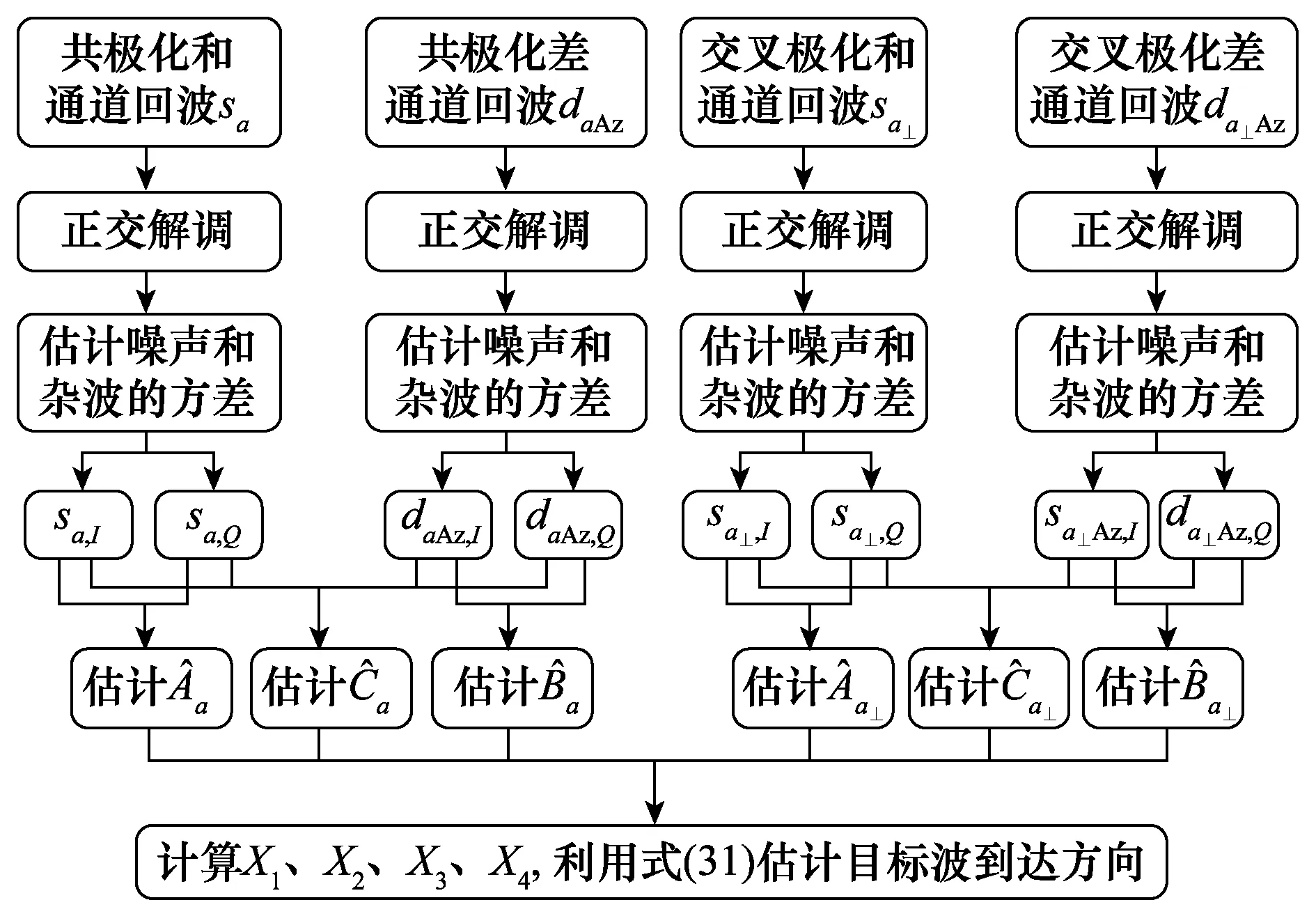
图2 估计目标角度算法流程Fig.2 Main workflow of estimate the target’s angle

值得指出的是,选择式(31)目标角度的两个值,可以通过文献[3]所提出的方法来判断,在检测到箔条质心干扰的同时,该方法同时可以确定舰船目标和箔条干扰角度的相对大小。

4 仿真实验

根据前面章节的理论分析,本小节通过仿真实验定量分析不同的脉冲数、信干比(signal-to-interference ratio,SIR)、信噪比(signal-to-noise ratio,SNR)以及箔条云分布等因素对本文所提方法估计目标角度性能的影响,并与其他文献方法进行比较。

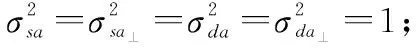
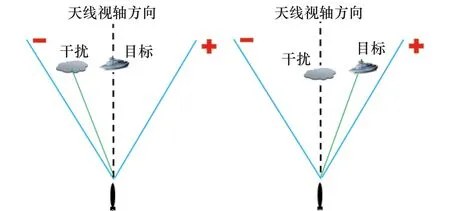
图3 仿真实验中目标和干扰相对位置关系示意图Fig.3 Sketch map of the relative position of target and interference in the simulation experiment

图4给出了不同的脉冲数、SIR和SNR对本文所提方法估计目标角度性能影响的仿真结果,蒙特卡罗仿真实验次数为5 000。图4(a)定量分析了不同脉冲数对目标角度估计性能的影响,仿真参数设定为:共极化通道中目标平均功率为30 dB,SIR=-4 dB;交叉极化通道中目标功率约为22.8 dB,假设箔条云为均匀球面分布,则有共极化通道中箔条干扰平均功率是交叉极化通道的3倍[18],即交叉极化通道箔条干扰功率约为20.2 dB。从图4(a)可以看出,即使固定了SNR和SIR,随着脉冲数N=4到N=12的增加,估计目标角度的均方根误差(root mean square error,RMSE)减小,这是因为随着脉冲数增加,对应式(25)～式(30)中回波信号的二阶统计量估计越准确,因而求得的目标角度误差越小。图4(b)给出了不同SIR对目标估计角度性能的影响,仿真参数设定为:共极化和交叉极化通道目标平均功率分别为25 dB和23.8 dB,N=8。质心干扰中形成的箔条云RCS一般是舰船目标RCS的2～3倍[2],故在仿真实验中SIR的取值范围可设为[0.3, 0.5], 即SIR∈[-5 dB,-3 dB]。从图4(b)中明显看出,SIR越大,估计目标角度的RMSE越小,这对抗箔条质心干扰是有利的,因为导弹在跟踪目标过程中,单脉冲跟踪系统根据估计目标的角度来调整天线轴指向目标方向,随着跟踪时间的推移,会出现波束切割箔条云的情况[19],相比于目标和箔条都在波束内部的情形,在这种情况下,SIR变大,估计目标角度的误差更小,这有利于对目标的测角估计。图4(c)分析了不同SNR对目标角度性能的影响,仿真参数设定为:N=8,SIR=-4 dB,共极化通道中目标平均功率是交叉极化通道的1.2倍。图4(c)标签中的SNR数值是从共极化通道计算得到的。从图4(c)中可以看出,SNR越大,估计目标角度的RMSE越小,SNR从20 dB增大到25 dB时,估计目标角度的RMSE得到了平均约0.023的改善,当SNR达到25 dB以上,继续增大SNR到30 dB,估计目标角度的RMSE改善的平均值仅约0.001。因此,仿真实验表明,本文所提的方法在中高SNR(如25 dB以上)情况下,可以获得较好的估计性能。

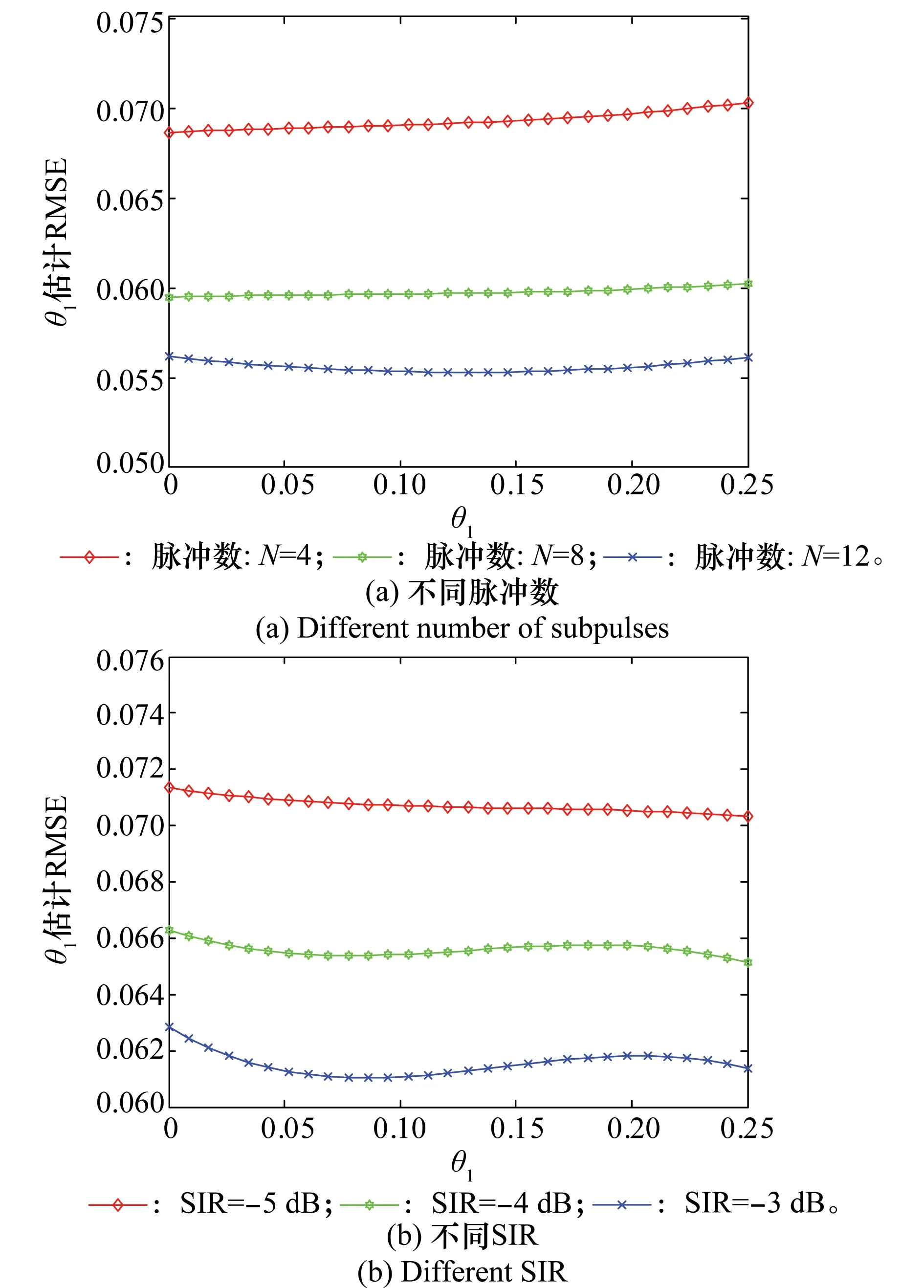
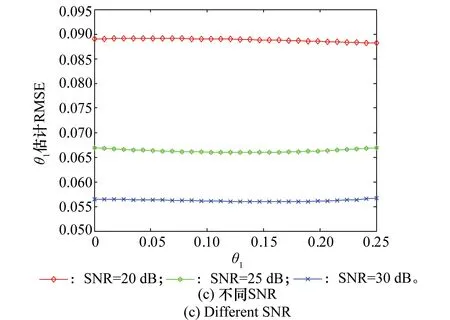
图4 不同的脉冲数、SIR和SNR对本文所提方法估计目标角度的性能影响 Fig.4 Effect of performance of the angle estimator for various values of subpulses, SIR and SNR

图5给出了不同的Δθ(即,舰船目标与箔条干扰的分开角度大小)对角度估计性能的影响,仿真参数设定为:脉冲数为8,共极化通道中目标平均功率为25 dB,SIR=-4 dB;交叉极化通道中目标功率约为23.8 dB,箔条云的分布类型为均匀球面分布。从图5中明显看出,Δθ越大,角度θ1的RMSE越大,这与文献[8]和文献[10]得出的结论是一致的。针对这种情况,文献[8]给出了一种跟踪策略:当Δθ小于半个和波束宽度时,用一组脉冲数可有效地跟踪目标;而当Δθ介于半个和一个和波束宽度之间时,用两组连续脉冲数跟踪目标效果会更好。

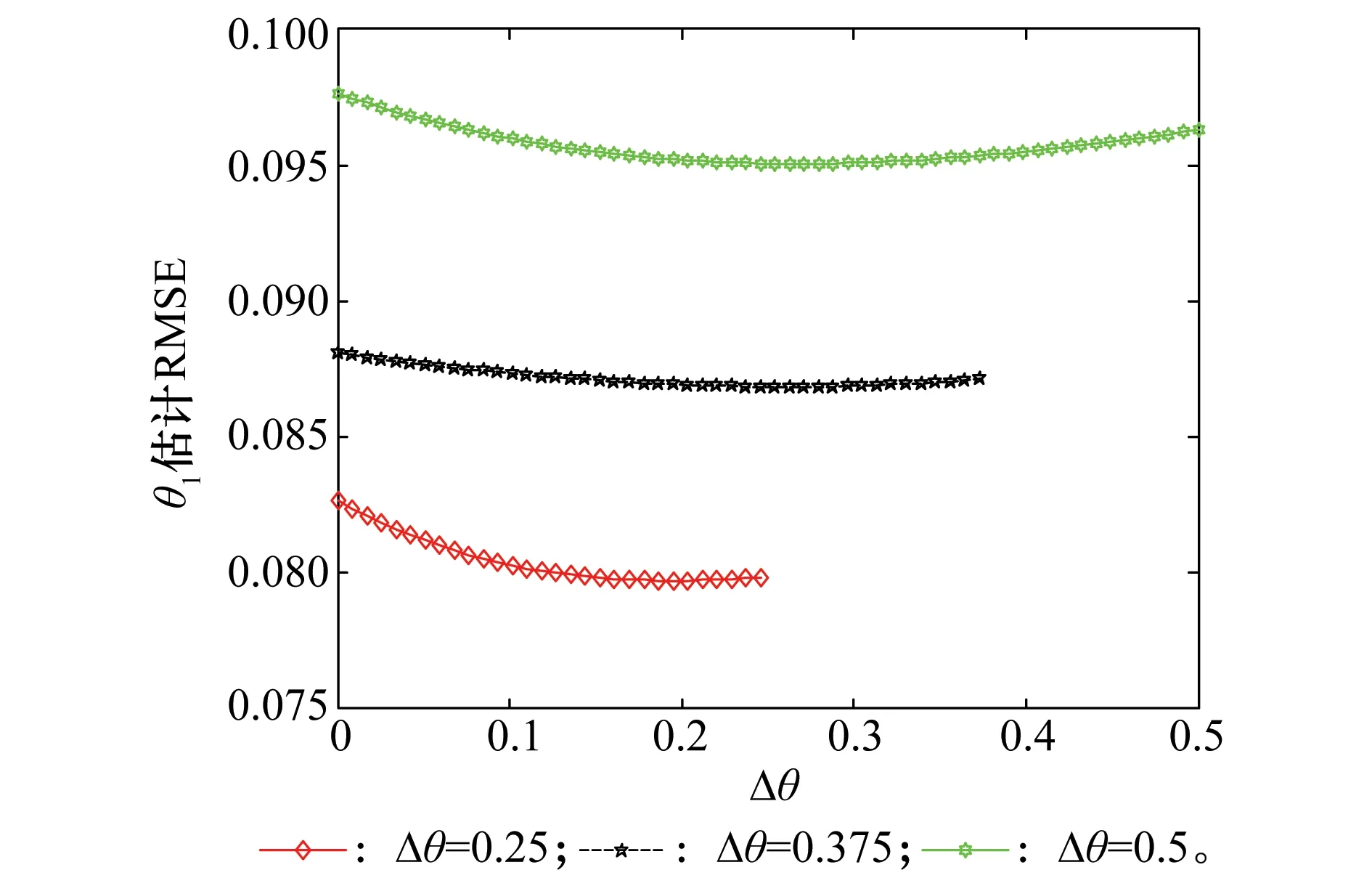
图5 不同的Δθ对角度估计性能的影响Fig.5 Effect of different Δθ on angle estimation

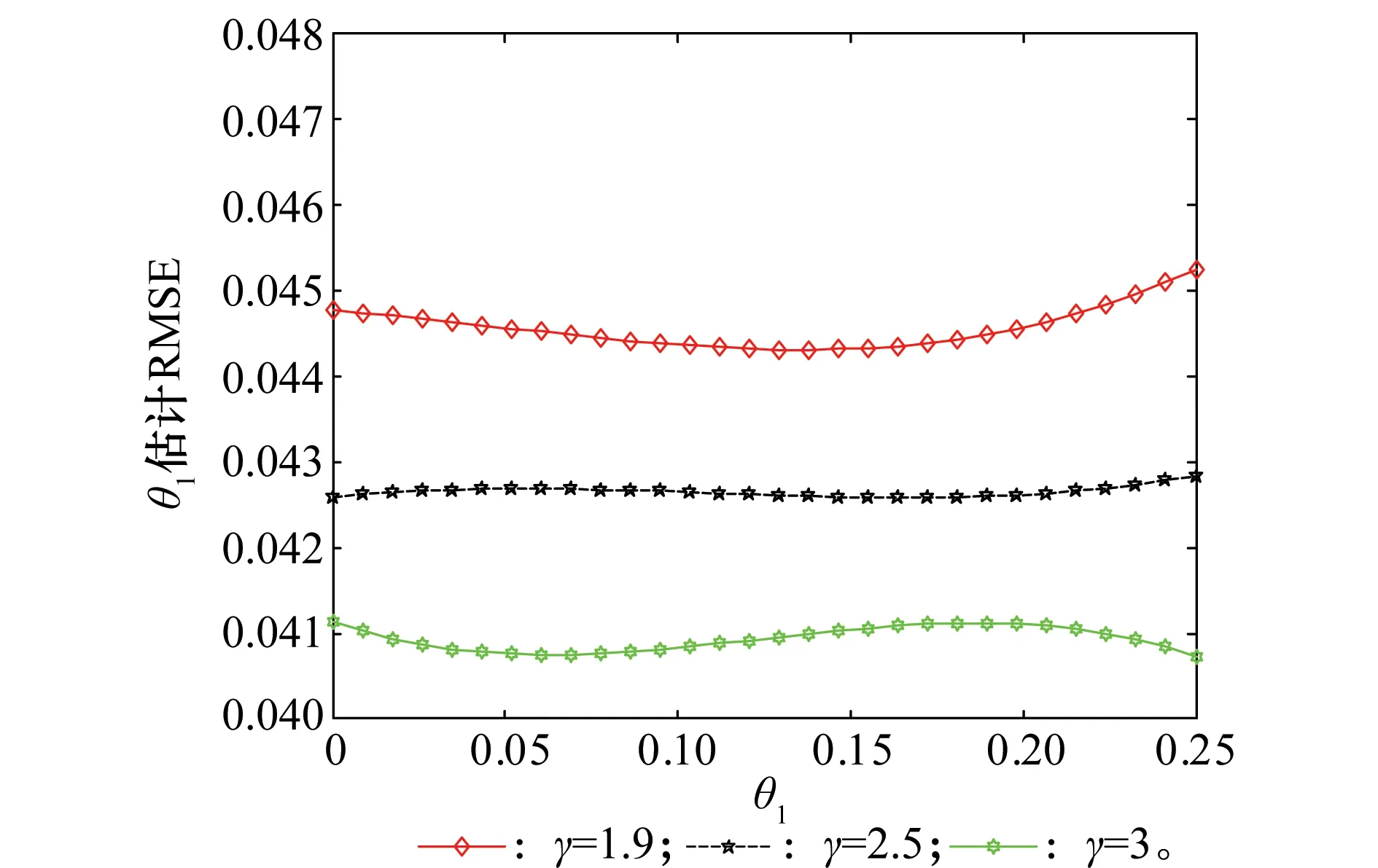
图6 箔条云分布对角度估计性能的影响Fig.6 Effect of chaff clouds’ distribution on angle estimation

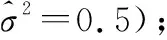
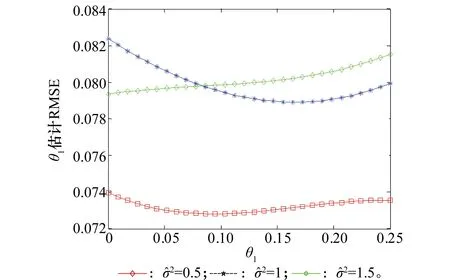
图7 噪声方差估计偏差对角度估计性能的影响Fig.7 Effect of estimate bias of the noise variance on angle estimation

为验证本文所提方法的估计性能,现与文献[8]的Blair方法、文献[9]的ML方法、文献[10]中的NM2方法以及文献[11]所提方法进行估计性能对比。仿真实验中,考虑两个斯威林II型目标,两个目标的角度差θ1-θ2=0.25,假设目标2为箔条干扰,箔条分布类型为球面均匀分布,各通道的噪声方差均为1,且估计准确。做3组仿真实验。第1组仿真实验参数设定为:SNR=20 dB,SIR=-5 dB,N=4;第2组仿真实验参数设定为:SNR=25 dB,SIR=-4 dB,N=8;第3组仿真实验参数设定为:SNR=30 dB,SIR=-3 dB,N=12,交叉极化通道中两目标的平均功率各自比共极化通道的低约3 dB。Blair方法、ML方法和NM2方法只考虑共极化通道回波信号。在3组仿真参数设定情况下,图8给出了本文方法与NM2方法、ML方法、Blair方法和文献[11]所提方法估计目标1的角度性能对比仿真结果(目标2的角度估计性能的仿真结果与目标1类似,故文中没有给出仿真结果)。在3种对比方法中,均假设各自的先验信息是已知的,即在NM2方法、ML方法和Blair方法中,两个不可分辨目标的RCS比值是已知的,在文献[11]方法中,箔条干扰的极化比是已知的。从图8的仿真结果中,可以看出:①随着子脉冲数增多,SIR和SNR增大,5种方法的估计性能均有所提高;②每组仿真结果中,ML的估计性能最佳,但该方法需要采用二维数值搜索方法来获得目标的角度,计算复杂度较大[10],不利于实时处理;③本文方法低于NM2方法的估计性能,这是因为本文所提方法在NM2方法的思路上,巧妙利用了极化信息维度,从而解决了NM2方法需预先知道两个不可分辨目标的RCS比值这一先验信息的问题,从3组仿真实验容易看出,随着子脉冲数增多,SIR和SNR增大,两者的估计性能基本接近,例如,在图8(c)中,本文所提方法估计目标角度的RMSE仅比NM2方法平均约低0.003;④从图8中可以看出,对于Blair方法,在θ1=0时,Blair方法的估计性能与ML方法相当,随着θ1的变化,Blair方法在θ1两端(即θ1=0和θ1=2.5)的估计性能比中间部分要好,出现这种情况的原因是为了确保估计目标角度有实数解,Blair方法给出了一些边界限制条件[8],此外,与NM2方法一样,Blair方法也需要预先知道两个不可分辨目标的RCS比值的先验信息;⑤文献[11]方法对箔条干扰的极化比的估计精度依赖性较大,在中低SNR的情况下,该方法估计性能比本文所提方法要差一些,当高SNR的情况下(见图8(c),SNR=30 dB),由于能够较准确地获得极化比的估计值,从而文献[11]方法估计精度优于本文所提方法。值得指出的是,在箔条质心条件下,由于舰船目标和箔条干扰是不可分辨,因而箔条干扰的极化比通常难以获得,文献[11]指出,极化比通常由经验值获得,在这种情况下,本文所提方法比文献[11]方法更实用一些。综上所述,相比其他4种方法,本文提出方法在无需目标或干扰的先验信息条件下,计算复杂度小,实用性较好,且估计目标角度的总体性能比较稳定。

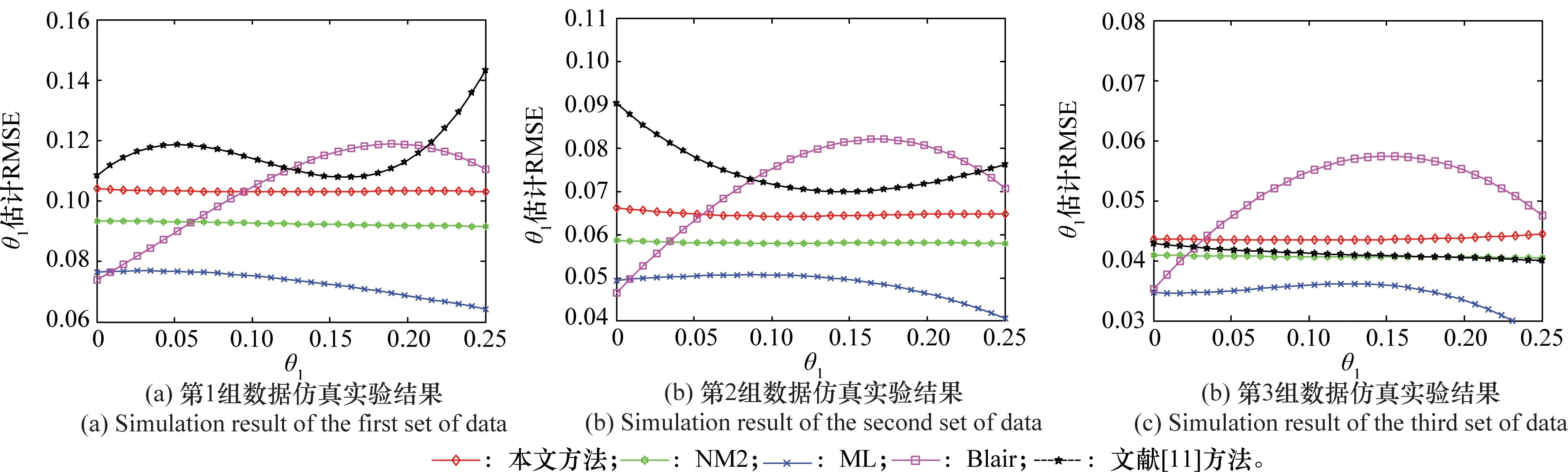
图8 本文方法与其他文献方法估计目标角度性能对比Fig.8 Compare the performance of the angle estimator with the other methods

5 结 论

本文在传统的单脉冲雷达系统的基础,利用极化信息,阐述了一种双极化和差信号模型,在此基础上,提出了一种基于极化单脉冲雷达估计目标角度的方法。该方法无需预先获取目标和干扰的先验信息,且在不同的脉冲数、SIR、SNR以及不同箔条分布类型的条件下,估计性能良好,是一种简单、实用的参数估计方法。理论分析和仿真实验均表明,在箔条质心干扰的情况下,该方法估计目标角度的可行性和有效性。值得指出的是,在反舰应用场合中,假设海杂波服从高斯分布,这与实际情况不是很吻合,这正是下一步将要研究的问题。