行星传动柔性销均载特性分析
2018-07-27
(中国飞机强度研究所,陕西 西安 710065)
0 引言
国内外行星传动系统均载措施主要有控制公差,提高制造、安装精度;中心构件浮动的均载措施;弹性构件均载技术[1-2]。柔性销技术属于弹性构件均载技术,它将行星轮固定在柔性的行星架上,达到行星齿轮间的载荷均布。柔性销能够在圆周方向独立承受弯曲,这样无论传递扭矩多大,都比较有利于行星齿轮间的载荷均匀分配[3]。
1 结构组成
柔性销具有扭转顺从性,通过双悬臂结构实现:两个切向力施加于柔性销行星齿轮上时,行星架上悬臂销轴的弯曲引起的角度挠度可以由来自相反方向的悬臂套筒弯曲所引起的角度挠度抵消,这种结构保证了齿向的均载性[4-5]。结构如图1。
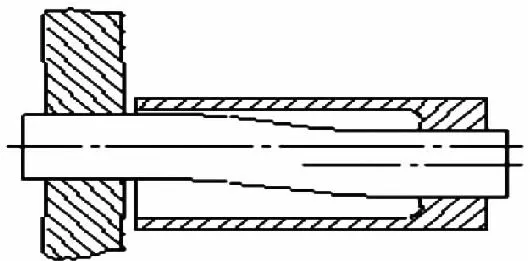
图1 柔性销双悬臂结构示意图
2 模型建立
2.1 模型简化
模型结构:柔性销轴、行星架简化模型、行星齿轮简化模型。三维结构如图2。
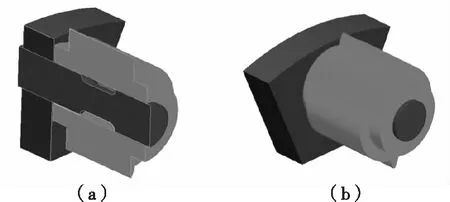
图2 柔性销三维简化模型
2.2 边界条件及载荷
以某行星轮系受载情况作为模拟工况,载荷大小:686.946 kN;柔性轴与行星架及轴套结合面处是过盈配合,利用FEA软件ANSYS接触模块模拟,并定义初始过盈量;柔性轴与行星架及轴套两端焊接部位采用节点耦合模拟;行星架(部分)侧面全约束;齿轮与内齿圈、太阳轮啮合面受力大小与方向均相同,如图3。
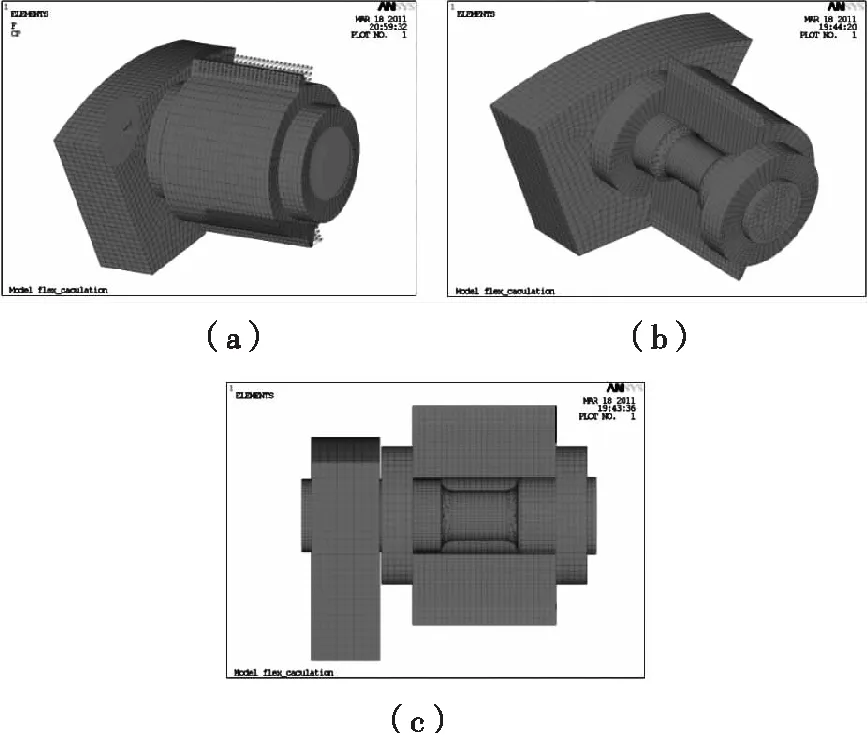
图3 柔性销结构有限元载荷及边界条件设置
3 计算结果
以下分别列出100%载荷和50%载荷时候,柔性销轴的变形规律。并根据计算结果,提取了柔性轴中心线的位移曲线。
3.1 100%载荷
100%载荷时,有限元计算结果如图4、图5。
用最小二乘法对柔性销轴右侧悬臂结构位移进行拟合,得到变形函数:y=1.204+0.00285x,从而得到行星架上悬臂销轴的弯曲引起的角度挠度为0.1633°,相对于周向线位移2.288 mm,此角度挠度可忽略不计。因此,100%载荷时柔性销具有较好的扭转顺从性。
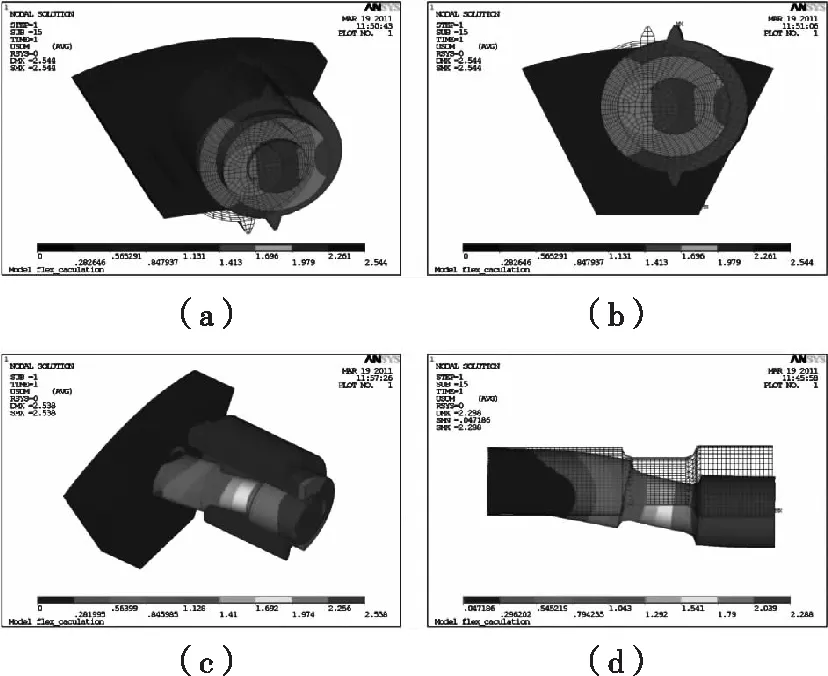
图4 100%载荷时柔性销轴整体位移云图
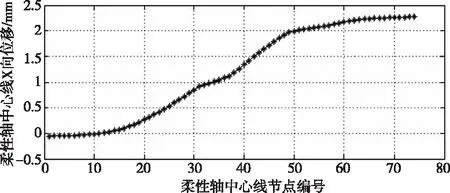
图5 100%载荷时柔性销轴中心线上节点位移分布曲线
3.2 50%载荷
50%载荷时,有限元计算结果如图6、图7。
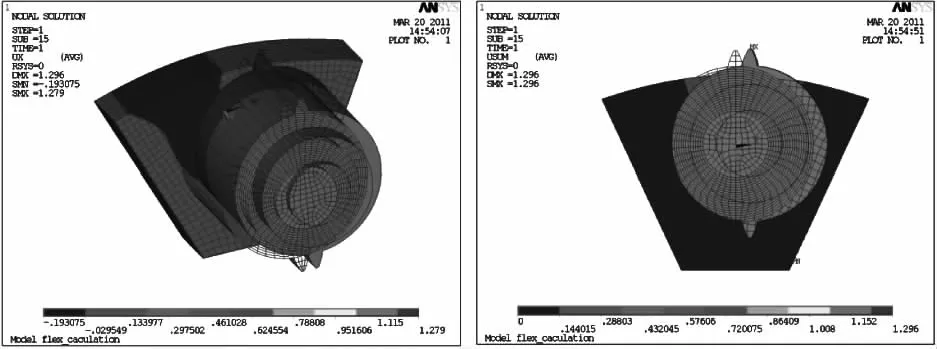
图6 50%载荷时柔性销轴整体位移云图
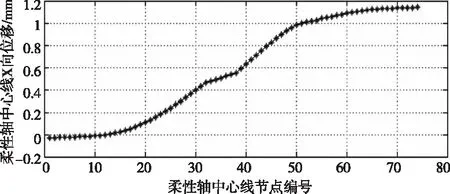
图7 50%载荷时柔性销轴中心线上节点位移分布曲线
参照图7中坐标系,采用最小二乘法对柔性销轴右侧悬臂结构位移进行线性拟合,得到变形函数:y=0.482+0.002623x,从而得到行星架上悬臂销轴的弯曲引起的角度挠度为0.1503度,相对于周向线位移1.195mm,此角度挠度可忽略不计。因此,50%载荷时柔性销具有较好的扭转顺从性。
4 均载特性
本文采用集中参数法建立行星传动系统动力学方程[6],如图8。将行星传动系统各构件看做刚性体,支承处、回转副和啮合副处刚度及阻尼用等效弹簧表示。假设:不计齿轮啮合时摩擦力的影响;原动机和负载的惯性、输入和输出扭矩的波动忽略不计;采用集中质量模型,相同结构具有相同的物理参数及几何参数;忽略各构件轴向移动自由度和非轴向扭转自由度(模型中考虑的因素:太阳轮、N个行星轮、内齿轮、行星架的横向振动和轴向扭转,齿轮啮合综合误差,齿轮副啮合间隙,啮合刚度)因此,每个构件有三个自由度:2个径向移动自由度和1个轴向扭转自由度,整个系统有3(3+N)个自由度。
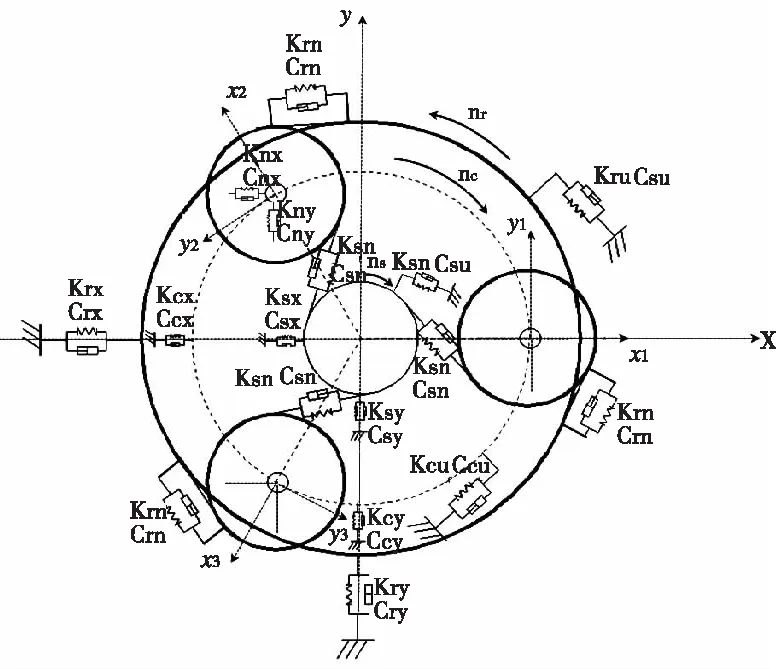
图8 行星传动多自由度动力学模型
计算得柔性销支承刚度kn=1.67×106N/m,带入多自由度动力学模型,其他参数不变,求解得到方程数值解,最终得到柔性销动力学均载特性,如图9。
从图9可看出系统动力学载荷分配不均匀系数为1.04。可见采用柔性销均载装置具有较好的均载特性。
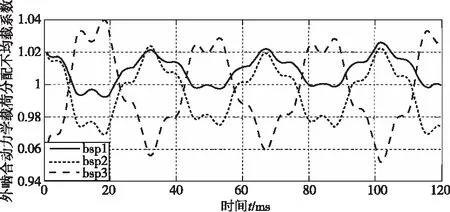
图9 柔性销均载系统动力学载荷分配不均匀系数
5 结论
通过对行星传动柔性销结构模拟计算,得到以下结论:1)柔性销结构具有较好的扭转顺从性;2)柔性销结构的行星传动系统具有较好的均载特性。
