考虑不同加载条件的粉砂质泥岩损伤特征

张向东，曲 直，李 军

(辽宁工程技术大学土木与交通学院, 辽宁 阜新 123000)

0 引 言

随着基础设施的不断建设，在矿山、隧道、硐室等工程建设过程中，会遇到各种类型的软岩。粉砂质泥岩是一种常见的软岩，粉砂质泥岩的矿物组成主要由黏土矿物、长石、石英等组成，其形成过程是经过长时间的挤压、脱水、重结晶等作用后形成的钙泥质胶结或者是粉泥质结构，其物理性质具有易裂、易碎性、透水性较差等。因此，在围岩开挖的过程中，开挖的扰动、爆破的震动必将引起岩石中微裂隙或孔洞的继续发展或扩张，岩石发生劣化，岩石的力学性质发生改变，造成岩石的损伤。在施工过程中，安全隐患频出，经常成为施工者的一个重大难题。在软岩损伤方面，国内外大量学者针对岩石的力学性质及其本构方程做了大量的研究。杨永杰等[1]对灰岩进行了三轴压缩声发射试验，利用声发射参数，对三轴压缩状态下的灰岩进行损伤演化分析；李杭州等[2]通过假设软岩微元强度分布统计概率，对软岩的统计损伤变量进行了定义，并依据统一强度理论建立了三轴应力状态下的软岩损伤统计本构模型；朱杰等[3]通过大量的岩石瞬时和蠕变试验，以及损伤力学和流变力学的相关理论，建立了一个能反映白垩系地层冻结软岩力学特性的本构方程。

邓肯-张(Duncan-Chang)模型是J M Duncan等人提出的岩土类材料的非线性双曲线本构模型[4-5]。项良俊等[6]对新岩滑坡膨胀性软岩Duncan-Chang模型及归一化特征进行了一系列的研究；王军保等[7]采用三轴压缩试验，研究砂岩的力学特性，并对Duncan-Chang模型进行了改进。尽管上述学者对Duncan-Chang模型进行了大量的研究，以及模型优化，很少有人将Duncan-Chang模型应用到软岩领域或是研究与软岩加载过程产生损伤的相关问题。

由大量的工程实例表明[8]，矩形巷道在开挖的过程中会出现应力集中现象，造成巷道变形，其中顶、底板主要发生拉应力集中，两帮主要发生压应力集中。若顶底板的岩体较为坚固，两帮为较为软弱的粉砂质泥岩，在高压应力作用下，顶板岩体强度较高，损伤较小，顶板变形不是很明显；两帮岩体较软弱，岩石在高压应力作用下，岩石内部的微裂隙或孔洞将会发生较大的发展或扩张，变形较大，两帮被压坏，其破坏主要表现为巷道片帮，所以开挖矩形巷道后，要及时对两帮进行加固处理。由于巷道开挖后的应力释放，围岩应力重新分布，岩体围压将会改变，并且不同的开挖方式以及循环进尺将会直接影响巷道的变形大小和变形速率，因此掌握不同围压、不同加载速率下粉砂质泥岩的加载损伤特性对巷道的施工与支护具有重大意义。

本文通过对Duncan-Chang模型变换得到了用切线模量表达的损伤变量表达式，将其与本文提出的切线模量符合负指数关系的控制方程相结合，建立了考虑损伤特性的粉砂质泥岩的加载应力-应变损伤演化模型。并通过实验加载以及超声检测来验证模型的合理性。

1 粉砂质泥岩损伤演化模型

邓肯-张(Duncan-Chang)模型是一种广泛地用于分析岩土体受到荷载时变形特征的本构模型。该模型是依据康纳尔(Kondner)大量土的三轴试验结果建立起来的，发现三轴加载过程中的加载曲线具有双曲线特征，可以表示成如下形式[9]。

(1)

式中：σ1、σ3分别为轴压和围压；ε1为轴向应变；a、b分别为与偏应力和轴向应变有关的试验曲线拟合参数，可用以下关系进行确定。

(2)

式中：E0为初始变形模量或初始切线模量。

设(σ1-σ3)f为岩土体发生破坏时的偏应力，若应力-应变曲线接近于双曲线，则根据一定应变所对应的偏应力(如ε1=15%)作为(σ1-σ3)f，若加载曲线存在峰值，(σ1-σ3)f选用峰值点所对应的偏应力，根据摩尔库伦准则，(σ1-σ3)f可表示为：

(3)

式中：φ为内摩擦角；c为黏聚力。

若定义Rf为破坏比(或强度发挥系数)，其形式可由下式来表示。

(4)

根据加载过程中，任意点的应变与偏应力之间的关系为：

(5)

式中：Et为加载曲线上任一点的切线模量。

对式(1)进行变形，考虑式(5)的应力-应变关系，Duncan-Chang模型可变成如式(6)的形式。

(6)

试验初始时的试样的无损切线模量为E0，加载过程中发生损伤时的切线模量为Et。法国学者Lemaitre根据等效应变假设，提出了损伤变量D可用式(7)来确定[10]。

(7)

对式(6)进行变形，D可以表示为：

(8)

考虑到粉砂质泥岩的本构方程是围岩加载过程的应力应变关系，所以从损伤力学的角度出发，损伤力学认为，损伤材料的本构关系可由无损伤材料的本构关系导出，只需将应力转换成有效应力形式[11]，如式(9)。

(9)

以实测的应力-应变曲线的斜率作为泥岩的初始剪切模量E0,泥岩的损伤本构方程可以表示为：

(10)

根据大量实验研究表明[12]，岩石的切线模量Et受偏应力的影响，切线模量Et会随着偏应力的增加而逐渐衰减，最终趋近于0(图1)。由试验规律曲线假设切线模量Et随偏应力的变化符合负指数规律，建立如下方程：

(11)

图1 切线模量-偏应力关系曲线Fig.1 Deviatoric stress-tangent modulus curve

式中：a、q为控制方程的参数，参数a与式(2)中的意义相同，决定了初始模量E0的位置；q决定了衰减的速率。

若令σ=σ1-σ3，由式(10)和式(11)可得：

(12)

由式(8)可得：

(13)

(14)

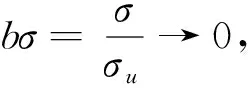
(15)

对式(8)进行变形可得：

(16)

对模型(15)两边进行求导，将σ=0代入可得：

(17)

图2 不同参数的损伤应力-应变曲线Fig.2 Damage stress-strain curve of different parameters

2 实验测试与模型验证

2.1 试件的采集与加工

为了分析粉砂质泥岩在不同围压以及不同加载速率加载条件下的变形特性和强度特性，本文采用TAW-2000电液伺服岩石三轴试验仪(图3)对试件进行加载试验。该设备组成部分包括：门款式刚性主机、系统油源、围压控制系统、自平衡压力室、控制柜、电控箱、主机等。

图3 TAW-2000电液伺服岩石三轴试验仪Fig.3 TAW-2000 electro-hydraulic servo rock triaxial equipment

粉砂质泥岩选自山西省大同市南阳坡煤矿，测试试件利用锯石切割机切割并在磨石机上打磨，最终制成尺寸为Φ50 mm×100 mm的标准圆柱形试件。

试验方案：采用TAW-2000电液伺服岩石三轴试验仪对不同围压、不同加载速率条件下的试件进行三轴加载试验。其中，加载速率设为0.10 mm/min、0.15 mm/min和0.20 mm/min，围压设为5 MPa、10 MPa和15 MPa。

2.2 测试结果及分析

通过TAW-2000电液伺服岩石三轴试验仪对粉砂泥岩试件进行三轴加载试验，并得到其在不同围压和不同加载速率下所对应的应力-应变曲线(图4)。

图4 不同围压条件下三轴加载应力-应变曲线Fig.4 Stress-strain curves under different confining pressures

由图4曲线可以看出，在加载速率相同条件下，极限偏应力随围压的增大而增大，并依次经历弹性变形阶段、峰前塑性变形阶段、破坏阶段和残余强度阶段。在围压相同的条件下，例如当围压为σ3=15 MPa时，分别采用加载速率0.10 mm/min、0.15 mm/min和0.20 mm/min时峰值所对应的应变分别为1.72%、1.46%、1.10%，极限偏差应力值分别为144.929 MPa、165.718 MPa、187.341 MPa， 随着加载速率越大，粉砂质泥岩的峰值应变值逐渐减小，抗压强度明显提高，这是由于岩石内部矿物间排列是紧密镶嵌的。当一个矿物受力时，必然会引起周边矿物移动，使矿物间的初始裂隙和新裂隙逐渐扩展，在较小加载速率条件下裂隙有较充足的时间发生调整和发展，最终由于变形较大使软岩破坏，其强度较低，峰值应变较大；而当加载速率较大时，岩石内部的微裂隙来不及充分发展，由于加载速率较大，导致矿物间剧烈挤压使较坚硬的矿物破坏，因而强度较大，峰值应变较小。

由试验后的破坏试件可知，最后试件破坏形式主要是单斜面的剪切破坏，偏应力作为岩石破坏的主要驱动力，偏应力的大小等于第一主应力σ1与围压σ3之差。根据图4应力应变曲线，以围压σ3作为最小主应力，以偏差应力峰值与围压之差作为轴向应力σ1，画出所对应的极限状态下的Mohr应力圆，通过作出试件破坏时的主应力Mohr应力圆的包络线(即为抗剪强度曲线)(图5)，即可得出试件在不同加载速率条件下的力学参数，结果见表1。

图5 抗剪强度包络曲线Fig.5 Envelope curve of Shear strength

ν/(mm·min-1)c/MPaφ/(°)0.105.88480.158.69490.2010.6850

3 加载损伤分析

对于破坏比Rf的确定，大量学者对其做了相关的研究，破坏比Rf取值因人而异。为此Duncan等人在总结大量资料的基础上建议采用如下方法确定[13]。

(18)

式中，下标70%、95%分别表示偏应力(σ1-σ3)的大小等于发生破坏时应力差(σ1-σ3)f的70%、95%时所对应的数据。

根据图4的测试结果，曲线存在峰值，采用峰值作为破坏应力差(σ1-σ3)f。粉砂质泥岩在不同围压下的破坏比计算结果见表2。

由表2可以看出，破坏比Rf是一个随围压变化而逐渐演变的一个参量。由于围压会改变岩石内部的微裂隙、孔洞的愈合程度，因此当岩石处在不同围压的条件下时，岩石受到荷载作用而产生的损伤程度将发生变化，并且损伤变量D是一个随围压σ3和轴压σ1变化而变化的参量。由式(4)和Duncan给出的经验公式(18)，损伤变量的经验演化公式为：

(19)

由式(19)可知，损伤变量是一个无量纲参量。由式(8)可以看出D是受σ=σ1-σ3影响的参量，并且σ3对岩石的损伤发展有一定的抑制作用，而σ1会加剧岩石的损伤。加载的偏应力越大，岩石的损伤越严重。由于峰后阶段软岩已经破坏，不同试件由于其自身裂隙、节理分布不同，损伤程度差异较大，本文主要研究粉砂质泥岩在不同围压和加载速率条件下破坏前的损伤变化规律(峰前部分)，根据试验加载曲线并结合式(19)，绘制出在不同加载速率条件下的损伤变量D与偏应力σ1-σ3的关系图像(图6)。

表2 破坏比Rf计算结果

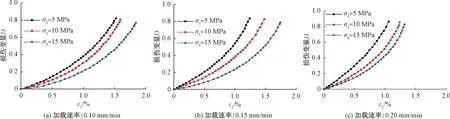
图6 损伤变量与应变的关系Fig.6 Relationship between damage variable and strain

图6可以看出，损伤变量是一个随ε增加而逐渐增加的参量，在加载速率为0.20 mm/min时，当所施加围压分别为5 MPa、10 MPa和15 MPa时的损伤变量值分别是0.862、0.851、0.829，围压越大损伤变量值越小，这与围压对岩石的破坏有抑制作用的事实相一致；在围压为15 MPa时，加载速率分别为0.10 mm/min、0.15 mm/min和0.20 mm/min时所对应的损伤变量分别为0.768、0.789、0.829，加载速率增大粉砂质泥岩的损伤加剧。这与加载速率较大的破坏试件，裂隙数较多的客观事实相一致。因此，本文提出的损伤关系模型符合粉砂质泥岩加载过程的损伤规律。

4 模型及实验结果正确性验证

在工程中，为了快速、简洁的测验混凝土的密实程度以及内部裂隙常常采用超声波方法进行检测，国内外学者利用超声波对岩石的力学性质以及损伤程度做了大量研究。本文采用TICO混凝土超声波测试仪对加载过程中的试件进行损伤超声检测(图7)。

图7 TICO混凝土超声波测试仪Fig.7 TICO concrete ultrasonic tester

张树光[14]利用超声检测法对冻土损伤过程进行测试，根据超声波在发生损伤材料的传导速度衰减特征，认为损伤变量数值与材料的密度以及波速的二次方有关，建立了如式(20)所示的声速与损伤变量的关系。

(20)

式中，ρt为损伤材料的密度，ρ0为无损材料的密度，为损伤材料的超声波速，为无损材料的超声波速。

由于加载过程中试件质量与体积接近不变，因此ρt≈ρ0。在温度为20 ℃条件下，经测试试件在无损状态下的平均波速为2 430 m/s，在加载速率为0.20 mm/min时，围压分别为5 MPa、10 MPa和15 MPa时对加载过程中各阶段试件进行超声检测，应变每增加0.1%测试一次波速，绘制出波速ν与应变ε1的关系(图8)。

由超声波速测试结果并结合式(20)可得各个阶段试件的损伤变量值(图9)。由超声检测结果显示可知，在围压分别为5 MPa、10 MPa和15 MPa时，加载损伤峰值分别为0.873、0.864、0.843，均略大于三轴压缩试验测试的损伤变量值，其原因在于超声检测时将试件从三轴试验机上取下，在取下的过程中，试件围压被卸载，内部微裂隙继续扩张、裂化，损伤加剧。由此可以看出本文所提出的的粉砂质泥岩损伤本构模型以及试验结果能较真实的反映粉砂质泥岩的损伤特性。

图8 应变与波速的关系Fig.8 Relationship between strain and wave velocity

图9 超声波检测损伤演化曲线Fig.9 Damage evolution curve by ultrasonic testing

5 结论

本文通过对Duncan-Chang模型变换得到了用切线模量表达的损伤变量的表达式，将其与本文提出的切线模量符合负指数关系的控制方程相结合，建立了考虑损伤特性的粉砂质泥岩的加载应力-应变损伤演化模型。

(1)三轴压缩试验表明：不同围压条件下，损伤变量随围压增加而减小；不同加载速率条件下，损伤变量随加载速率增加而增加。

(2)本文利用TICO混凝土超声波测试仪对加载过程中的粉砂质泥岩进行超声检测，根据超声波在发生损伤材料的传导速度衰减特征，得到了加载过程中粉砂质泥岩的损伤规律。