降雨条件下抗滑桩边坡三维稳定性分析

李 宁，刘冠麟，许建聪，张利伟，李玉成，王 晓

(1.上海理工大学环境与建筑学院，上海 200093；2.同济大学地下建筑与工程系，上海 200092；3.四川省城乡规划设计研究院，四川 成都 610081)

0 引 言

我国有新老滑坡30余万处，其中灾害性的约1.5万处，每年发生的滑坡数以万计，经济损失高达100亿元以上[1]。抗滑桩作为一种有效的边坡支挡结构，以其结构形式简单、刚度大、抗力大、施工便利等优点被广泛应用于大型滑坡灾害的治理中[2]。长期以来，国内外学者针对抗滑桩边坡进行了大量的研究工作：Cai[3],雷文杰[4],Wei[5]及年廷凯[6]采用有限元强度折减法对桩间距、桩位、桩的刚度等对抗滑桩边坡稳定性及滑面形式的影响进行了研究；吕庆[7]，杨雪强[8]分别采用平面应变有限元法及理论方法对抗滑桩桩后土拱效应的作用机理及发育规律进行了研究；申永江[9]对两种常用的双排抗滑桩的抗滑效果进行了研究，并指出刚架双排桩能够更好的发挥抗滑效果；Wang[10]采用离心模型试验对面荷载作用下抗滑桩边坡的渐进破坏进行了研究。

但以上研究均未涉及降雨作用，而大量的滑坡实例表明，降雨尤其是暴雨是诱发滑坡等地质灾害的主要因素，尤其是我国南方以及中南、西南地区雨量充沛，这些地区的山地或人工边坡在雨季常发生滑坡，因此，这些地区的抗滑桩多工作于降雨环境中，并在降雨条件下发挥其抗滑作用，因此对降雨条件下的抗滑桩边坡进行研究，将更有助于我们了解抗滑桩的实际工作情况。此外，在降雨条件下抗滑桩边坡稳定性的变化规律如何？是否与前人在不考虑降雨时得到的变化规律相似？这将直接关系到前人在不考虑降雨时得到的抗滑桩边坡的规律性结论能否直接用于多雨地区抗滑桩的设计实践，是目前亟待解决的问题之一。

为此，本文在对ABAQUS软件进行二次开发的基础上，结合典型边坡算例，开展了降雨条件下抗滑桩边坡的三维稳定性分析，着重研究了降雨条件下设桩位置及桩间距对边坡安全系数的影响，并与不考虑降雨条件时的影响规律进行了比较，进而找出两者在变化规律上的不同之处并阐明其原因，以期为多雨地区的抗滑桩设计提供参考依据。

1 降雨条件下抗滑桩边坡稳定性分析原理

本文采用饱和-非饱和渗流结合有限元强度折减法对降雨条件下抗滑桩边坡的稳定性进行数值模拟，以下将对其计算流程以及计算过程中涉及的降雨边界处理进行详述：

1.1 降雨入渗边界的处理

降雨入渗边界比较复杂，以往的数值模拟中多采用定边界进行处理[11]，而朱伟[12]与陈学东[13]通过土柱降雨入渗试验，指出降雨入渗边界是随降雨时间而不断变化的动边界，其具体形式要根据地表径流情况来确定：

(1)未出现径流时

此时降雨将全部入渗，因此其边界流量应满足：

(1)

kr——相对渗透系数；

xj——坐标；

h——压力水头；

ni——坡面的外法线方向向量；

p——降雨强度。

其边界上的水头应满足：

h≤0

(2)

(2)出现径流时

此时的降雨不能全部入渗，未入渗部分将在坡面形成径流，由于坡面具有一定坡度，假定径流可迅速流走而未形成积水，则此时边界上的水头应满足：

h=0

(3)

其边界上的流量应满足：

(4)

针对以上降雨边界条件，本文采用迭代算法对其进行处理：

(1)首先将上一时步降雨边界所处的状态(有无径流)作为下一时步降雨边界迭代的初始条件。

(2)假如处于无径流状态，则首先以式(1)为定解条件进行计算；然后将得到的边界上节点的水头计算结果代入式(2)进行校核，如全部满足则转入下一时步计算；若不满足则转入步骤(3)。

(3)假如处于有径流状态，则首先以式(3)作为定解条件进行计算；然后将得到的边界上节点的流量计算结果代入式(4)进行校核，如全部满足则转入下一时步计算；若不满足则转入步骤(2)。

(4)重复步骤(2)、(3)，直至降雨边界上所有节点均满足相应的定解及校核条件。

1.2 降雨条件下抗滑桩边坡稳定性分析的有限元强度折减法

有限元强度折减法为边坡稳定性分析提供了一条比较有效的途径[14-15]，从计算角度来看，降雨条件下的强度折减法比较复杂，其计算工作量较大[16]，同时，对降雨边界的迭代处理及桩-土间的相互作用更加大了其计算的复杂性。为了更加准确、高效的利用强度折减法进行降雨条件下抗滑桩边坡的稳定性分析，本文以大型有限元计算软件ABAQUS为平台，对其进行二次开发，来完成降雨条件下抗滑桩边坡稳定性的分析，基本思路如下：

(1)根据1.1节中的迭代算法，基于ABAQUS软件，利用Python语言对其单一流量边界进行二次开发，然后进行降雨条件下抗滑桩边坡的非稳定渗流分析，得到降雨过程中每一时刻的边坡水压分布。

(2)由(1)中得到的边坡水压分布，根据Lu等[17-18]提出的饱和、非饱和相统一的土体有效应力公式，利用Python编制程序求得由水压形成的等效结点力，并施加于各有限元节点上。

(3)根据李宁等[19]提出的基于场变量的有限元强度折减法，采用USDFLD.f对ABAQUS进行二次开发，对降雨条件下抗滑桩边坡进行强度折减有限元分析，得到降雨过程中每一时刻的抗滑桩边坡安全系数。

其计算流程图见图1。

图1 计算流程图Fig.1 Calculation flow chart

2 数值模拟及成果分析

前人[3,6]在不考虑降雨条件下对抗滑桩的桩间距及桩位对边坡稳定性的影响进行过研究，本节将在前人研究的基础上，进一步对降雨条件下抗滑桩桩距及桩位对边坡稳定性的影响进行研究；并把考虑降雨与不考虑降雨条件下得到的结论进行比较分析。

2.1 计算模型及材料参数

选取一典型抗滑桩边坡算例(图2)，边坡坡度为1∶1.5，坡高为10 m，地基深度为10 m；抗滑桩距坡脚的水平距离为Lx=7.5 m，桩径D=0.8 m，桩间距为S=3D，抗滑桩端部嵌固于基岩或稳定地层中。根据对称性，选取宽度为0.5S，抗滑桩取一半作为计算模型来进行三维数值模拟[6]。

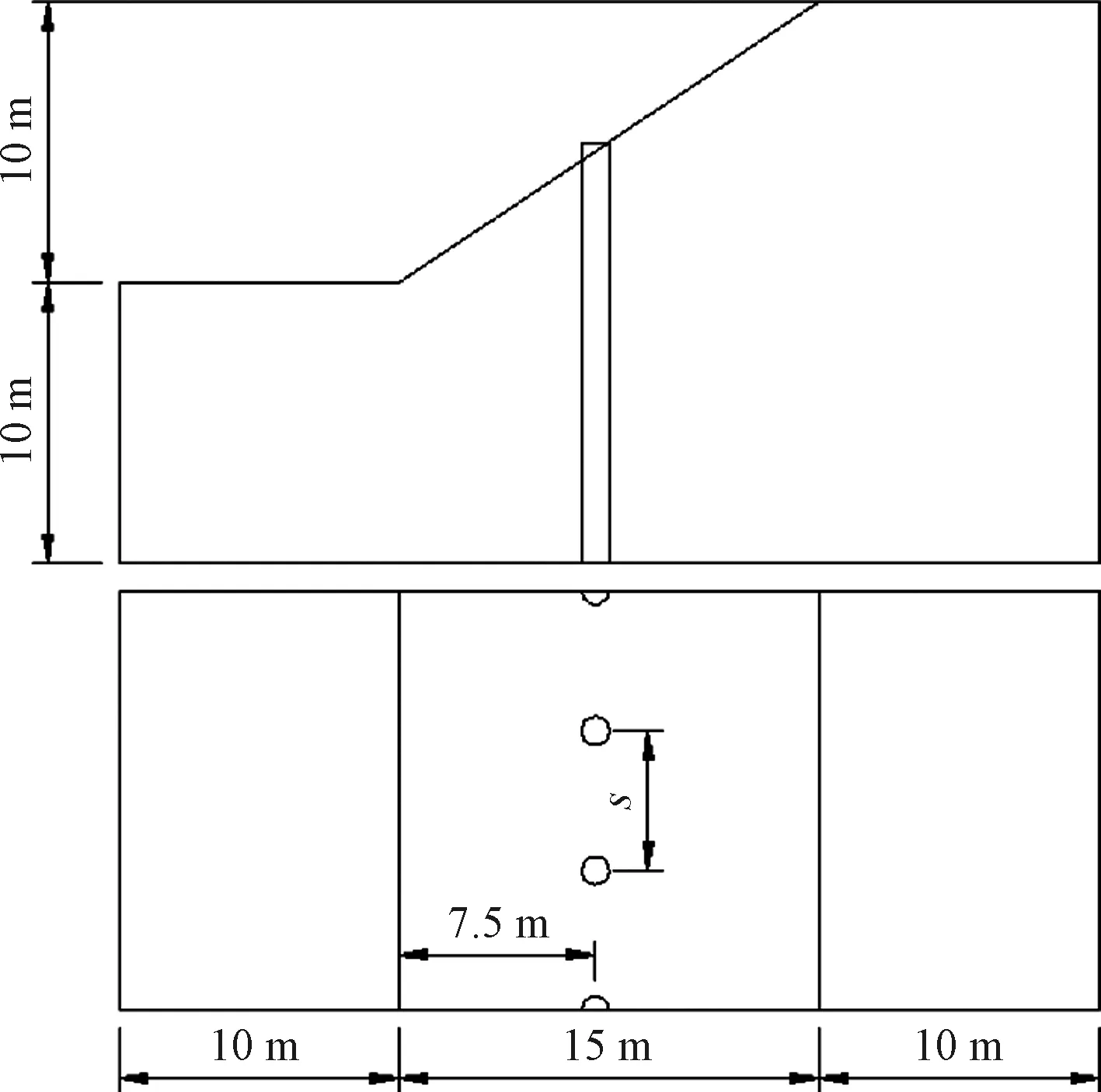
图2 抗滑桩-边坡模型Fig.2 Stabilizing pile-slope model

边坡土体与抗滑桩的力学参数参考文献[6]进行选取，具体见表1，桩-土之间的摩擦系数亦参考该文取为0.3；由于文献[6]中的数值模拟并未考虑降雨的影响，因此该文并未给出土体的水力特性参数，本文参考文献[6]中的土体类型，选取相应的土体水力参数[20](表2)。边坡中的初始地下水位位于坡脚处，且边坡上部施加强度为10 mm/h的降雨，持续10 h。

表1 桩、土力学参数

表2 土体水力特性参数

图4 不同桩径比边坡破坏时两桩中心剖面处的等效塑性应变云图Fig.4 Equivalent plastic strain contour for different pile diameter ratio

2.2 桩距对抗滑桩边坡稳定性的影响

采用前述算例，在抗滑桩处于坡中位置时，改变桩间距S值，使其在1.2D～6D之间变化，分别对不考虑降雨与考虑降雨条件下桩距对边坡稳定性的影响进行研究。

2.2.1不考虑降雨时

图3为不考虑降雨时抗滑桩边坡安全系数随桩间距与桩径比(S/D)(简称桩径比)的变化曲线，由图可知，在不考虑降雨时，随着桩间距的增加，边坡的安全系数将逐渐减小；这与Cai等[3]、年廷凯等[6]得到的结论是一致的。

以下通过不同桩径比条件下边坡破坏时的等效塑性应变云图，来对图3中得到的安全系数变化规律进行进一步的分析。

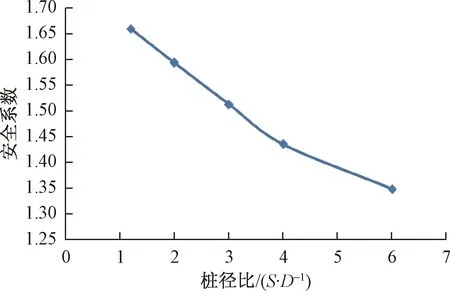
图3 不考虑降雨时安全系数随桩径比变化曲线Fig.3 Variation of safety factor with pile diameter ratio regardless of rainfall

图4给出了不同桩径比条件下边坡破坏时两桩中心剖面处的等效塑性应变云图，从图4中可以看出，当S=1.2D时边坡的滑面在抗滑桩位置处被分隔为上、下两部分，说明此时抗滑桩由于桩间距较小而发挥挡墙的功效，将边坡上下部土体隔离开，无法形成至上而下的贯通滑面，从而使整个抗滑桩边坡体系具有较高的安全系数；随着抗滑桩桩间距不断增加，当S=2D时，土体的塑性区在抗滑桩位置处沿桩长方向向边坡深处发展，说明此时抗滑桩的群桩效应在发挥作用，抗滑桩不断调动桩周土体并与之共同抗滑；随着抗滑桩间距进一步增加，当S=4D及S=6D时，边坡的滑面已基本发展为一条至下而上连续贯通的曲面，说明此时抗滑桩的群桩效应已不明显，因而整个抗滑桩边坡体系的安全系数较低。这与图3得到的结论是吻合的。

以上分析说明当不考虑降雨时，桩间距越小，抗滑桩边坡体系的安全系数越高。

2.2.2降雨条件下

图5为不同降雨时间安全系数随桩径比(S/D)的变化曲线，由图5可知，在降雨条件下，当桩间距从1.2D增加到2D时，此时的边坡安全系数是增加的，而当桩间距继续增加，从2D增加到6D时，边坡安全系数将逐渐减小；这说明在降雨条件下，当桩间距很小时，边坡安全系数反而会降低，抗滑桩并不能起到很好的抗滑效果，这与2.2.1节中不考虑降雨时得到的结论是不同的。

图5 考虑降雨时安全系数随桩径比变化曲线Fig.5 Variation of safety factor with pile diameter ratio under rainfall conditions

以下通过不同降雨时段桩间距为1.2D及2D条件下边坡内水压分布规律，来对造成这种差异的原因进行分析。

图6给出了不同降雨时段，对应于不同桩间距的边坡内的水压力分布图。为了便于确定浸润线的位置，将非饱和区采用黑色显示，饱和区仍保持彩色显示，两者的交界处即为浸润线。由图6可知，在相同的降雨时段，桩间距越小，浸润线的升高幅度越大，其饱和区的水压越大，非饱和区基质吸力越小。这主要是因为抗滑桩的渗透系数非常小，其存在阻碍了雨水在边坡土体中的流动，这相当于减小了坡体的有效排水断面，且桩间距越小，设桩位置处的有效排水断面越小；而有效排水断面越小，越不利于坡体中入渗雨水的流动及排出，从而导致其浸润线升高幅度越大。

因此在降雨条件下，一方面通过2.2.1节中的分析可知，较小的桩间距有利于抗滑桩边坡整体抗滑性能的发挥；而另一方面，通过本小节(2.2.2小节)的分析可知，较小的桩间距会大幅减小坡体的有效排水断面，造成入渗雨水不能及时排出，从而抬升了坡体内的浸润线，导致边坡土体的饱和程度增加，从而造成下滑力增大，阻滑力减小，进而对抗滑桩边坡整体抗滑性能产生不利影响；所以降雨条件下抗滑桩边坡的稳定性随桩间距的变化规律将由以上两方面因素共同决定，这在图5中也得到了反映。对于本节算例来说，当桩间距为2D时可以获得最大的安全系数。

2.3 桩位对抗滑桩边坡稳定性的影响

仍采用前述算例，保持桩间距S=3D时，改变抗滑桩在坡体中的位置，使抗滑桩距坡趾的水平距离Lx在3到12之间变化(采用相对位置ξ=Lx/L来反映这种变化，其中L为坡面水平长度)，分别对不考虑降雨与考虑降雨条件下桩位对边坡稳定性的影响进行研究。

2.3.1不考虑降雨时

图7为不考虑降雨时安全系数随桩位的变化曲线，由图可知，当设桩于坡中位置处(即Lx/L=0.5)，抗滑桩边坡体系获得最大的安全系数；当设桩于坡顶或坡脚处，抗滑桩的阻滑效果要小于坡中位置。这与文献[3]、[6]得到的研究成果是一致的。

图6 不同桩径比条件下的边坡水压分布图Fig.6 Pore pressure contour under different pile diameter ratio

图7 不考虑降雨时安全系数随桩位的变化曲线Fig.7 Variation of safety factor with pile position regardless of rainfall

以下通过不同桩位处边坡破坏时的等效塑性应变云图，来对图7中得到的安全系数变化规律进行进一步的分析。

图8分别给出了设桩于坡脚(Lx/L=0.2)、坡中(Lx/L=0.5)、坡顶(Lx/L=0.8)位置处边坡破坏时两桩中心剖面处的等效塑性应变云图。由图8可知，当抗滑桩位于坡脚位置时，滑面位于边坡的上部，说明此时主要发挥的是桩上部边坡土体的抗滑能力来维持整个抗滑桩边坡的稳定性；当抗滑桩位于坡中位置时，边坡的上部与下部均出现塑性区，且沿桩长向桩的深部发展，说明此时即可以充分调动桩上部边坡土体的抗滑能力，又可以将边坡上部的剩余下滑力通过抗滑桩传递到桩下部边坡土体及桩深部的稳定地层中，并充分调动桩下部边坡土体的抗滑能力来共同维持抗滑桩边坡的稳定性；当抗滑桩位于坡顶位置时，滑面位于边坡的下部，说明此时主要发挥的是桩下部边坡土体的抗滑能力来维持整个抗滑桩边坡的稳定性。

综上所述，相对于坡脚及坡顶位置，当将抗滑桩设置于坡中位置时，更容易调动抗滑桩上部边坡土体、下部边坡土体及抗滑桩深部稳定地层来共同抗滑，因此具有较好的抗滑效果。这与图7得到的安全系数变化规律也是吻合的。

图8 不同桩位处边坡破坏时两桩中心剖面处的等效塑性应变云图Fig.8 Equivalent plastic strain contour at different pile position

2.3.2降雨条件下

图9为考虑降雨时安全系数随桩位的变化曲线，由图可知，在降雨条件下，在坡中位置设置抗滑桩并未达到最佳的加固效果，而是在Lx/L=0.4处，也即从坡中向坡脚方向偏离1.5 m的位置设桩，可以使抗滑桩边坡系统获得最大的安全系数；此外，在坡脚位置处设桩比在相应的坡顶位置处设桩具有更好的加固效果，这与2.3.1节中不考虑降雨时得到的结论是不同的。

以下通过降雨条件下不同桩位处边坡内的流速矢量分布规律，来对造成这种差异的原因进行分析。

图10分别给出了设桩于坡脚(Lx/L=0.2)、坡中(Lx/L=0.5)、坡顶(Lx/L=0.8)位置时在降雨6 h后边坡内的流速矢量图。由图可以看出，坡体内部的雨水向坡脚处汇集并排出坡体，且无论抗滑桩是处于坡脚、坡中还是坡顶位置，其流速矢量均在坡脚处较大，这说明在坡脚处水头变化速率较大，具有较高的水力梯度，因此将对坡脚产生较大的朝向边坡临空面方向的渗透作用力，这对坡脚的稳定是不利的；如果此时将抗滑桩置于坡脚部位，抗滑桩将起到稳固坡脚的作用，有助于增强其稳定性；因此在坡脚位置处设桩比在相应的坡顶位置处设桩具有更好的加固效果。这在图9中也得到了反映。

图9 考虑降雨时安全系数随桩位的变化曲线Fig.9 Variation of safety factor with pile position under rainfall condition

图10 降雨6h后不同桩位处边坡内的流速矢量图Fig.10 Velocity vector at different pile position after 6 hours of rainfall

对于最佳设桩位置，一方面，通过2.3.1节中的分析可知，将桩设置于坡中位置更容易调动抗滑桩及边坡土体共同抗滑；而另一方面，由于降雨会对坡脚的稳定性产生不利影响，将桩置于坡脚位置将更容易稳定坡脚。因此，综合考虑这两方面因素，降雨条件下最佳桩位应位于坡中与坡脚之间。

以上分析与图9得到的降雨条件下抗滑桩边坡的安全系数变化规律也是吻合的，对于本节算例来说，在降雨条件下，当在坡中向坡脚方向偏离1.5 m处设桩，可以获得最大的安全系数。

3 结 论

前人对抗滑桩边坡的研究多集中于无雨条件下，本文在前人研究的基础上，进一步对降雨条件下抗滑桩边坡的稳定性进行了研究，并通过与无雨条件下的研究结果进行比较，发现：

(1)当不考虑降雨时，桩间距越小，抗滑桩边坡体系的安全系数越高，这与Cai等[3]、年廷凯等[6]前人的研究成果是一致的；但是在降雨条件下，桩间距的减小会使坡体的有效排水断面减小，从而导致抗滑桩的抗滑效果得不到很好的发挥。因此在降雨条件下设置抗滑桩，既要考虑到桩间距减小对抗滑桩边坡稳定性带来的有利影响，又要考虑到桩间距减小导致桩后地下水位抬升而对抗滑桩边坡稳定性带来的不利影响，综合选取桩间距。对于本文算例，在降雨条件下，当桩间距为2D时可以获得最大的安全系数。

(2)当不考虑降雨时，将抗滑桩置于边坡中部时，具有较好的抗滑效果，这与Cai等[3]、年廷凯等[6]前人的研究成果是一致的。但是在降雨条件下，坡脚处会产生较大的渗流作用力，因此在设桩时，既要考虑抗滑桩与土体的共同抗滑效应的发挥，又要兼顾坡脚处的稳定，因此，将抗滑桩置于坡脚与坡中之间的位置能起到较好的抗滑效果。对于本文算例，在降雨条件下，当在坡中向坡脚方向偏离1.5 m处设桩，可以获得最大的安全系数。

(3)限于篇幅，本文只对一典型抗滑桩边坡算例在特定降雨条件下的稳定性进行了研究，得到的桩间距与桩位具有一定的局限性，对于复杂的边坡形式及降雨形式下的桩间距和桩位的确定仍需进行进一步研究。但是通过本文的论证可以看出，考虑与不考虑降雨所得到的抗滑桩边坡系统的稳定性随桩间距与桩位的变化规律是不同的，这也说明在多雨地区进行抗滑桩设计，必须充分考虑当地降雨情况，才能合理的进行抗滑桩的设计，这也是本文的主要目的。