圆锥曲线定值问题研究

广西桂林市中山中学 秦 勇

本文通过对圆锥曲线定值问题的研究，总结归纳了解决圆锥曲线定值问题的主要策略。

一、参数法

几乎所有的圆锥曲线定值问题都涉及参数的选取，必须通过参数作为中间量进行计算，最后消去参数，得到定值。

（1）求椭圆C的方程。

（2）E，F是椭圆C上的两个动点，如果直线AE的斜率与AF的斜率互为相反数，证明直线EF的斜率为定值，并求出这个定值。

（2）如图1，设AE的斜率为k，则AF的斜率为－k。

二、特殊值法

除了参数法之外，我们还可以用另一种方法求解定值问题，我们可以先在特殊情况下求出定值，然后我们再证明定值与特殊情况无关，在一般情况下也成立。

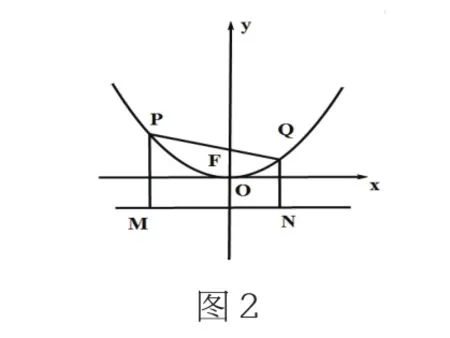
例2 过抛物线m：y=ax2（＞0）的焦点F作直线l交抛物线于P、Q两点，若线段PF与FQ的长分别为p，q，证明为定值。

证明：（1）在直线l与x轴平行的特殊情况下，有：

圆锥曲线定值问题是高中知识的一个难点，在详细研究了这类题型后，文中介绍了运用参数和特殊到一般这两种数学思想方法来解决圆锥曲线定值问题，希望能帮助读者从总体上认识圆锥曲线定值问题，增加在学习这部分知识时的信心，使我们在解决此类问题时很快地找到解题策略。