基于小波变换的ATM交易状态异常预警模型设计

南禹平 王健光

本文通过对ATM终端数据进行特征参数提取及小波变换信号放大的方法，建立ATM交易状态异常预警模型。模型建立采用多层分类，聚类分析等方法确定指标并提取特征参数；针对特征参数运用小波变换精确找出数据突变点及区间得到异常状态可能存在范围并建立联合预警函数。将故障程度分成高度预警、较高度预警、普通预警和情况正常四种预警等级进行信号预警。

一、特征参数构建

我们以某商业银行总行数据中心监控系统后台一至四月数据为样本，进行预警模型研究与构建。由于样本信息量庞大且存在信息杂糅，因此采用组间聚类分析方法对样本信息按照信息特征进行分类，并根据组间距离提取最具代表性三个指标即业务量、交易成功率及交易响应时间。

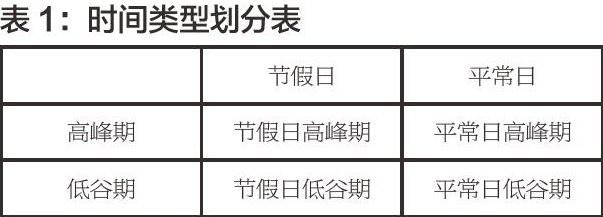
由于指标数据具有时间跨度大且取样密集的显著特点（见表1），我们采用二分法数据按时间跨度长短将时间类型大体分成四种：

由于比较不同组数据需使用相对量，而且本研究提供数据是时间序列数据，数据密集，可近似视为连续，为检验连续数据的突变值，本文采用平移标准差变化的方法处理状态特征參数指标，效果良好。

经检验，本研究提供数据当连续计算三个数据时效果最好，所以按照这种平移标准化的方式将两个状态特征参数成功率和响应时间标准化得到成功率的平移标准化值Xe和响应时间的平移标准化值X_S。

X=X_i-3+X_i-2+X_i-1/3

S_i=

二、信号的小波变换

由于数据特征分布具有非典型性（如图），交易量，特征参数与各种函数拟合程度均不明显。小波变换作为一种新的可达到时间域或频率域局部化的时频分析方法，具有空间局部性能，可聚焦于信号的局部结构，能很好地处理无典型函数分布特征的数据，因此对特征参数进行小波变换。小波变换步骤如下，首先设θ（t）是一个低通平滑函数，且满足条件：

假设θ（t）二次可导，并且定义中ψ（1）（t）和中ψ（2）（t）分别为θ（t）的一阶和二阶导数，以ψ（1）（t）和ψ（2）（t）为小波母函数。将小波母函数ψ（t）进行伸缩和平移得小波基函数： ψ_a，b（t）=a_-1/2ψ（t-b/a），a>0，b∈R

其中a为伸缩因子（又称尺度因子），b为平移因子。

通过以上小波变换，求解信号小波变换模的极值点，从而求出原始信号的突变点。通过对不同时期样本数据进行上述的小波变换，从各种形式的小波变换中选出最佳的参数，选择结果表2，表3所示：

根据小波变化参数运用MATLAB精确找出突变点及突变区间，（如图所示）并发现不同时期的特征参数小波变换结果具有明显差异。

三、交易异常状态模型设计

考虑到能够及时反映ATM故障并减少谎报误报的概率，并结合2.2中小波变换的结果，我们引入分段函数对不同类型，对不同时期的小波变换结果进行预警程度的度量。通过查阅相关文献，并结合实际检验情况，设立如下的分段预警函数：

其中，C_i（X_i）表示不同时期成功率预警函数，S_j（X_s）为不同时期响应时间预警函数，X_cX_s分别为成功率和响应时间的小波变换值，F（X）为联合预警函数，可以发现F（x）=3，2.5…，0.5，0，考虑到成功率与响应时间数据波动的特点，设置S_j（X_s）的值为C_j（X_c）值的两倍。

F（X）的不同取值表示了不同的预警状态，通过查找相关文献和进行数据分析，本文将预警程度分为四种。F（X）=3为高度预警，F（X）=2.5为较高度预警，F（X）=2为普通预警，F（x）<2为情况正常。

四、模型效果检验

通过对小波函数的相关参数进行变化，来观察函数的变化情况。选取3月24号高峰期早6点到晚10点的响应时间数据作为样本，分别变化小波函数的尺度因子（伸缩因子）参数a与平移因子参数b，代入MATLAB 2010中进行小波变换，发现结果与平常高峰期如3月31号高峰期的波形拟合度很高，从而说明模型具有较好的稳健性，能够正确识别并进行及时的预警。