朴素贝叶斯模型在法人银行机构不良贷款预测中的应用
2018-07-26刘翔鹏
刘翔鹏


商业银行信用风险管理一直是全面风险管理( ERM)的重要组成部分,对于地方法人银行机构而言,不良贷款预测分类是信用风险管理的重点和难点。针对我国中小法人银行面临的不良贷款信用风险问题,引入朴素贝叶斯模型对不良资产信用风险进行识别分类,并选取湖南S农商行和B农商行2017年末全部信贷数据进行实证。
金融是现代经济的核心,银行市现代金融的核心,现代商业银行在经营和发展过程中,因为筹集融通资金,中间环节会积累大量不良资产。由于历史上和现实上的原因,我国农信系统的地方法人金融机构累积了大量的不良资产,虽然经过央行票据置换和农商行改革已经置换、清收了大量的不良资产,但是由于地方法人银行机构信用风险管理能力较差,人才队伍培养滞后,故对不良资产的事前识别能力极弱。
目前国内银行业对不良资产信用风险评估方法主要是采用古典分析法和多元統计法。古典分析法是指银行经营者依赖一批训练有素的专家主观判断,对信贷项目进行判断打分,审贷会以此决策。多元统计分析的基本思路是根据历史积累的样本建立统计模型,对新样本发生的某种事件的可能性进行预测的方法,包括线性概率和判别分析法等。
以上所述方法虽然被广泛应用,但是他们只是针对某一方面如财务进行分析和统计,不能充分利用银行搜集的全面信息,尤其是一些边缘信息。大量的数据挖掘研究结果表明,很多边缘信息和侧面指标可以很好地补充单一财务指标的缺陷,使借款项目的特征更加鲜明,故本文引入朴素贝叶斯模型,试图用新办法解决信用风险识别、评估的旧问题。
一、模型设计
朴素贝叶斯分类的基础是对于给出的待分类项,求解在此项出现条件下各个类别出现的概率,哪个概率最大,就认为此待分类项属于哪个类别。该模型以简单的结构和良好的性能受到人们的关注,模型建立在类条件独立性假设的基础上:给定类结点后,个属性结点之间相互独立。根据朴素贝叶斯的类条件独立假设则有:P=(X|Ci)= (P(XKCi)
条件概率P(X1|Ci),P(X2Ci),…P(XKCi)可以从训练数据集中求得。根据此方法,对一个未知类别的样本X,可以先分别计算出X属于每一个类别Ci 概率P(X|Ci)P(Ci),然后选择其中概率最大的类别作为其类别。
朴素贝叶斯的正确步骤如下:
(1)设x={a1,a2,…,am)为一个待分类项,而a为该待分类项的每一个特征值。
(2)有类别集合C={y1,y2,…,ym}。
(3)计算P(y1|x.)P(y1x.)…,P(yn|x)。
(4)如果P(yK|x)=max{P(y1|x.)P(y2|x)…,P(yn|x},则x∈yk。
那么,现在的关键就是如何计算第三步骤的各个条件概率,可以按如下步骤计算:
(1)找到一个已知分类的待分类项集合,这个集合叫做训练样本集。
(2)统计得到各个类别下各个特征属性的条件概率估计,即P(a1|y1),P(a2|y1),…,P(am|y1);P(a1|y2),P(a2|y2),…P(am|y2)…
(3)如果得到在各个特征属性是条件独立的,则根据贝叶斯定理有如下推导。
P(yi|x)=P(x|yi)P(yi)/P(x)
分母对于所有类别为常数,因此只要将分子最大化即可,因为各特征属性是条件独立的,所以有:P(am|yi)P(yi)=P(yi)mΠj=1P(aj|yi)
二、实证分析
本文选取湖南永州境内S农商行和B农商行全部信贷数据作为实证样本。首先对数据进行处理,对缺损数据和重复数据进行了清洗,选取12450个样本,13个特征值作为有效数据。将数据库的英文字符和中文字符全部转化为双精度浮点型数据,然后利用虚拟变量函数对双精度浮点型数据全部进行编码,样本属性标签正常贷款和不良贷款分别用0和1表示。
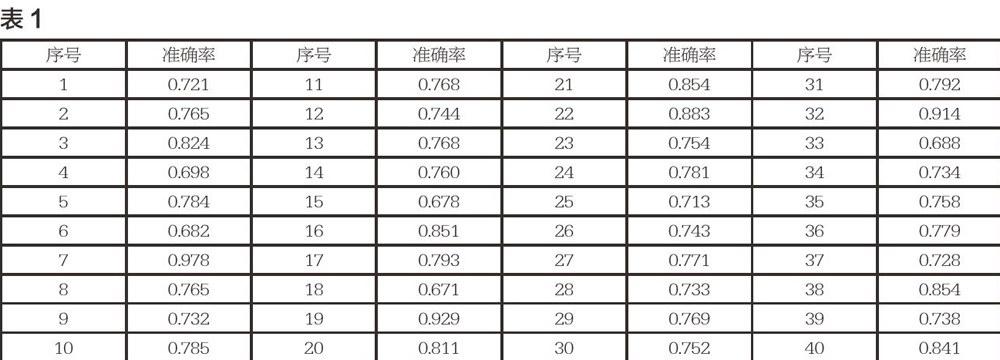
在实证环节,随机选取40%的样本作为测试样本,共进行40次交叉验证。40次交叉验证预测标签为1的不良贷款结果如下表1:
全部40次随机交叉验证的准确率均值为0.777,标准误差为0.069。由模型结果可以看出朴素贝叶斯分类器是健壮的,因为在从数据中估计条件概率时,这些点被平均。另外朴素贝叶斯模型可以处理属性值的遗漏问题,面对无关属性,该分类器依然是简单的,因为如果Xi是无关属性,那么P(Xi|Y)几乎要变成均匀分布,Xi的类条件概率不会对总的后验概率计算产生影响。属性如果相关可能会降低朴素贝叶斯分类器的性能,因为对这些属性,条件独立的假设已经不成立。
三、结论和建议
朴素贝叶斯模型的准确率很高,稳定性很强,在多次交叉验证后,得到较为稳定的准确率和较小的标准误差,故模型实用价值很高。但法人银行机构的关联交易和流动性状况是该模型不能识别的,股东的高额关联贷款给法人银行带来的信用风险是极大的,极端情况的流动性短缺会让法人银行机构经营困难,结合声誉风险,可能会被处置当局警告、早纠甚至接管。
