模拟自适应干扰对消系统对消速度分析*

(海军工程大学 舰船综合电力技术国防科技重点实验室，武汉 430033)

1 引 言

模拟自适应干扰对消系统是一种基于正交矢量合成的闭环干扰对消系统[1-2]。该技术目前主要应用于军事领域，对降低共平台辐射干扰，保证通信质量，提高频谱利用率具有重要意义[3]。

对消速度是模拟自适应干扰对消的重要性能指标。特别是对载波断续的信号，如跳频信号、振幅键控等，若对消速度过慢，在对消系统收敛过程中仍会有干扰信号影响通信，使得对消系统的实用性降低[4]。以跳频电台为例，现有跳频电台的跳频速率为100～1 000 hop/s，美国的CHESS电台跳频速率甚至可达5 000 hop/s。对于1 000 hop/s的跳频速率而言，要求对消所需时间要远小于1 ms。文献[4]给出了对消速度的基本数学模型。文献[5]在文献[4]基础上通过对实际系统进行分析，得出了在稳定情况下理想的模拟自适应干扰对消系统的对消速度模型。文献[6]对对消系统内的电调衰减器进行分析，得出了电调衰减器不同初始状态对系统对消速度的影响。文献[7]针对积分以及低通等多种不同的控制方式，得出了系统在稳定时过阻尼、临界阻尼以及欠阻尼时时域的误差收敛表达式，从误差收敛的角度反映了对消速度。

上述文献对系统对消速度模型的研究均基于理想的系统条件，对模拟系统的稳定性及电调衰减器的射频响应特性缺乏考量。相应地，其对消速度数学模型难以完整表征对消速度的特性。通过上述理想模型进行实用化对消系统参数设计，尤其是对消速度设计时，对于如何定量确定满足模拟系统稳定性条件下的最高对消速度，尚缺乏明确的设计方法。

本文对模拟自适应干扰对消系统的理想模型加入电调衰减器时域响应特性及环路的非理想特性的影响，通过仿真与实验，分析对消系统的对消速度性能，修正对消速度的理想数学模型。

2 自适应干扰对消速度

模拟自适应干扰对消系统的基本结构如图1所示[8]，实线与虚线标示了两个反馈控制环路。

图1 模拟自适应干扰对消系统结构Fig.1 Strucure of adaptive radiation interference cancellation system

通过求解系统时域的微分方程，系统的干扰对消比(Interference to Cancellation Ratio,ICR)可表示为[8]

ICR=20lg(1+K) 。

(1)

系统对消速度T可表示为[7]

(2)

式中：K是系统射频信号的环路增益，τ是系统时间常数。

3 理想对消速度数学模型的改进

3.1 反馈控制环路稳定性分析

以图中Q路为例，如图1中的实线所示，控制信号以乘法器为起点，经低通滤波器、电压电流转换电路、电调衰减器、功率合成器放大器1、合成器、误差反馈耦合器、放大器2、功分器，最后再回到乘法器，构成Q路反馈控制环路。

对于理想系统，系统会处于恒稳定或收敛状态[9]。对于模拟自适应干扰对消系统，上述反馈控制环路可视为由多级低通滤波特性的电路组成，如积分器电路、电压电流转换电路中的低通电路等，系统存在稳定性问题。定义系统低频分量Δf的环路增益kloop(Δf)，不妨设Q路乘法器误差端输入为

EF=acos[2π(f+Δf)t]+Eerrcos(2πf)。

(3)

式中：Eerr、a分别表示频率分量f、f+Δf的幅度。乘法器参考端输入为

CF=kokcERcos(2πf)，

(4)

ko、kc分别是正交功分器及耦合器的耦合系数。式(3)和式(4)相乘得乘法器输出中的Δf分量

(5)

E0为乘法器基准电压。对于高频量，低通滤波器以及电压电流转换电路的增益不会是固定值kτ和ks，而是kτ(Δf)和ks(Δf)。式(5)经过增益为kτ(Δf)的低通滤波器与增益为ks(Δf)的电压电流转换电路得

(6)

当不考虑电调衰减器自身插损，式(6)作为电调衰减器的控制信号与参考信号VR=koERcos(2πft)相乘得到

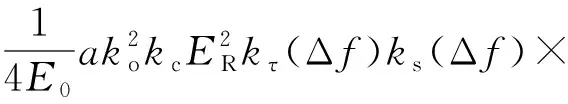
(cos[2π(f+Δf)t]+cos[2π(f-Δf)t])，

(7)

再乘以后续电路的增益得到

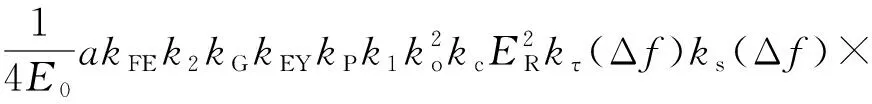
(cos[2π(f+Δf)t]+cos[2π(f-Δf)t])，

(8)

k1、k2、kG、kP、kEY、kFE分别为放大器1、放大器2、功分器、功率合成器、合成器、误差反馈耦合器各自的相关系数。对于f-Δf分量，也能得到式(8)结果，其则频率分量f+Δf的反馈环路增益可以表示为

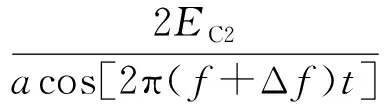
(9)

EC2表示EC中含频率分量f+Δf的项。根据负反馈电路的稳定性工作条件[9]，kloop(f+Δf)应当满足

(10)

式中：Δφloop表示反馈环路对频率分量Δf的相移。

3.2 电调衰减器响应速度分析

理想模型中，电调衰减器具有理想的幅相特性，对相同输入信号，其输出信号与控制信号始终呈线性关系，对信号没有延时，衰减与信号的频率无关。在实际模拟对消系统中，其衰减特性只在很小的范围内呈现线性，环路增益过大以及乘法器零漂等因素均可能使其控制电压进入饱和区，此时实际模拟对消系统在对消时会额外增加一段退饱和时间，会极大地降低对消速度[6]。

从电调衰减器的电路构成来看，电调衰减器射频部分主要是由PIN二极管构成的桥式电路或π形电路，控制部分由电压与电流的驱动电路组成[10]。其主要是利用PIN二极管的射频电阻随控制电流变化来控制衰减量，其电阻R与控制电流的关系如下：

(11)

式中：W是PIN二极管I区宽度，μ为PIN管载流子迁移率，τz为载流子寿命，IF为通过PIN二极管的直流电流。

当IF变化时，R随之变化，导致输出功率的变化，从而达到电控衰减。而PIN管在不同IF状态变化时，由于载流子的扩散与复合会有一定的响应时间，因此，PIN二极管对于射频信号幅度的调整是有一定响应时间的，相应地，电调衰减器对于射频信号的变化也有一定响应时间。假设电调衰减器从一个稳定状态进入另一个稳定状态时的响应时间为TD，则对消速度T满足

T≥TD。

(12)

3.3 对消速度修正模型

根据上述分析，实际模拟系统对消速度设计时，不仅需要满足稳定性条件，还要受到电调衰减器响应速度限制。因此，有必要对理想的对消速度计算模型进行修正。

首先引入稳定性条件，进行对消速度模型修正。对于实际模拟自适应干扰对消系统，式(2)未考虑反馈控制环路稳定性问题。

第二步，将对消速度公式修正为

(13)

进一步引入电调衰减器响应时间限制条件T≥TD，则修正的对消速度Tmod为

(14)

4 仿真与分析

4.1 电调衰减器响应时间仿真

搭建电调衰减器电路以及电压电流转换电路[11]进行仿真。为得到较精确的时域特性，其中PIN管模型利用的是Strollo模型[12]。

根据实际工作条件，参考信号为瓦级，经过功分器及耦合器后至电调衰减器射频输入端的功率为20～30 dBm，根据实际电路搭建的电调衰减器模型的控制电压线性工作区在-2～+2 V。在电调衰减器的射频输出端接纯阻性负载，测试电路如图1所示。利用方波信号作为驱动电路的控制信号，通过改变方波信号的上下电平，测试阻性负载前端的射频输出信号的波形，参数设置见表1。

图2 电调衰减器响应速度仿真测试示意图Fig.2 Sketch map of response time to electronic attenuator in simulation

仿真条件仿真参数备注方波控制信号高电平(Vhigh)/V2,1驱动电路线性工作的上限电压为2 V,额外再选取1 V进行对照低电平(Vlow) /V高于-2低于所设高电平,高于驱动电路线性工作的下限电压-2 V上升沿/ns1下降沿/ns1同时设定在10 μs时刻进入上升沿,210 μs时刻进入下降沿上电平宽度/μs200方波周期/μs400保留一定的时间裕量,使驱动电路能够响应完毕射频信号频率/MHz200,300,400超短频段典型信号频率功率/dBm0,10,20,30实际对消装置中进入电调衰减器射频输入端的功率为20～30 dBm初相0简化分析

改变射频输入信号的功率及频率对电调衰减器射频响应速度无影响，而改变控制电压对电调衰减器的响应速度影响较大。当射频输入功率为20 dBm、频率为30 MHz时，改变控制电压，仿真结果如图3所示。图3所用方波形的高电平Vhigh=2 V。通过改变方波信号低电平所得到的射频输出波形，图3(a)所示的是低电平与高电平的极性未变化时图像，图3(b)是高电平与低电平极性发生变化的图像。

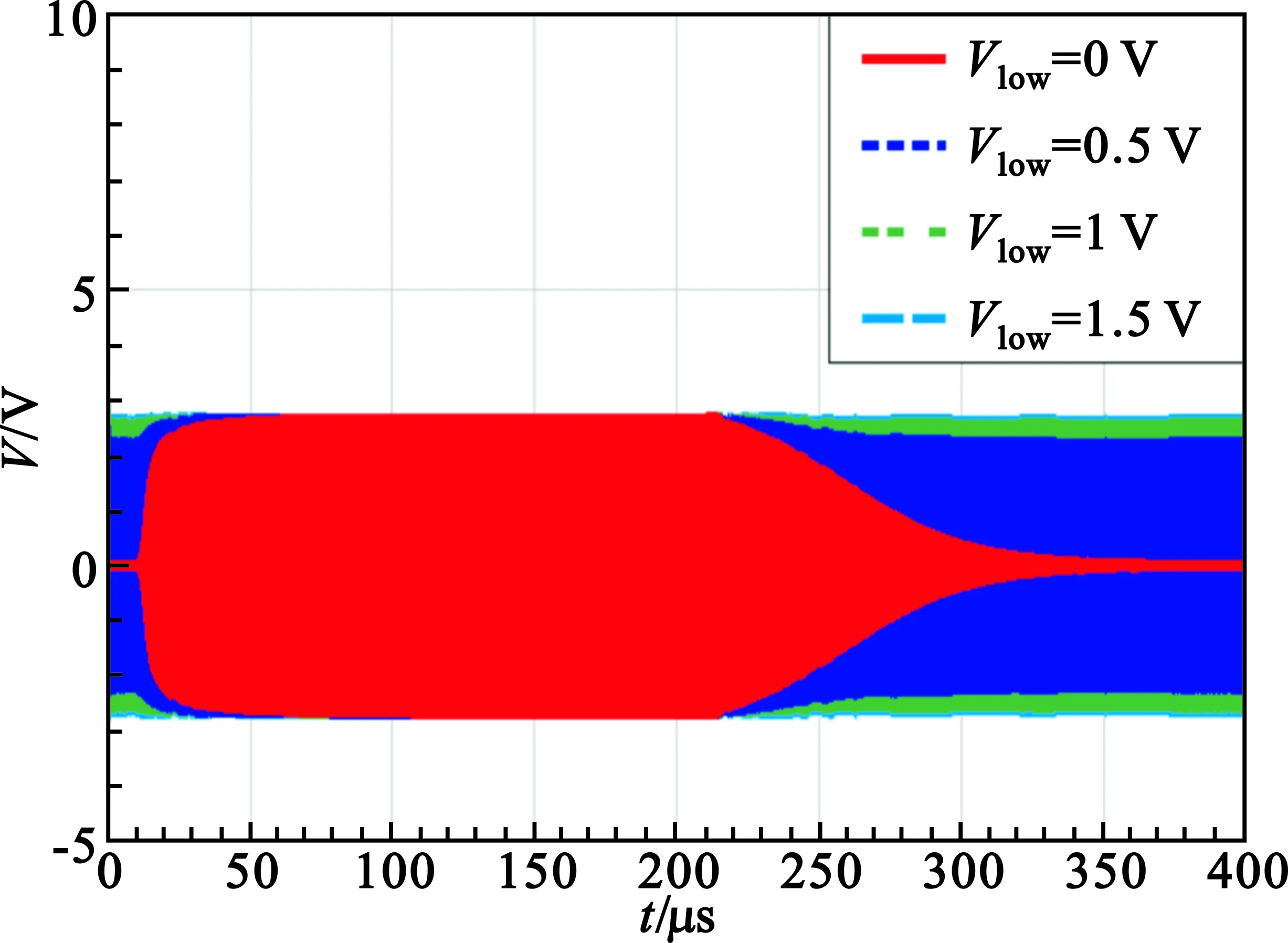
(a)低电平与高电平极性未变化

(b)低电平与高电平极性发生变化图3 不同控制电压条件下的电调衰减器响应速度仿真Fig.3 Response speed of electronic attenuator under different control voltage

由图3可知，电调衰减器的响应速度与控制电压变化的差值以及控制电压极性是否发生改变有关。当控制电压幅值变化极小且极性未发生改变时，其响应速度较快；当控制电压极性未发生但是幅值变化较大时，对方波信号的上升沿，其响应所花的时间小于50 μs，但是对方波信号的下降沿，其响应所花的时间在100 μs量级。当控制电压的极性发生改变时，由于对消系统所用电调衰减器是设计为双极性的，因此对于方波信号的上升沿以及下降沿其波形性质一致，其响应所花时间均在100 μs量级。事实上，由于对消系统是一个闭环负反馈控制系统，且由于前级滤波器的对于低频交流信号的滤波能力有限，控制电压不会是一个纯直流信号，对消系统完成对消所需时间远在100 μs以上，严重影响对消速度。

4.2 反馈控制环路仿真

由前面的分析可知，系统控制环路的振荡是由频率分量Δf引起的。系统控制环路内，各模拟器件对频率分量Δf的相移和足够大时，会使该频率分量满足振荡条件。实际系统中，频率分量Δf由于受到了控制环路中低通滤波器的滤波特性影响，其频率不会太高，而较低的频率引起的附加相移又不会达到系统振荡的条件，实际引起振荡的频率分量Δf一般处于kHz级别。对于该频率级别的频率分量，控制环路中的模拟器件的附加相移均研究较多，但对于电调衰减器对于控制信号中的具有的该频率分量Δf产生的相移研究较少。

现使驱动电路的控制信号为一直流量与交流量的叠加信号，使控制信号中的交流分量的幅值为0.1 V，直流量为0.1 V，射频输入信号的频率为300 MHz。为便于射频输出波形与控制信号的波形进行比较，射频信号的功率选为10 dBm。改变控制信号中交流分量频率，电调衰减器射频输出与控制信号的图像如图4所示。

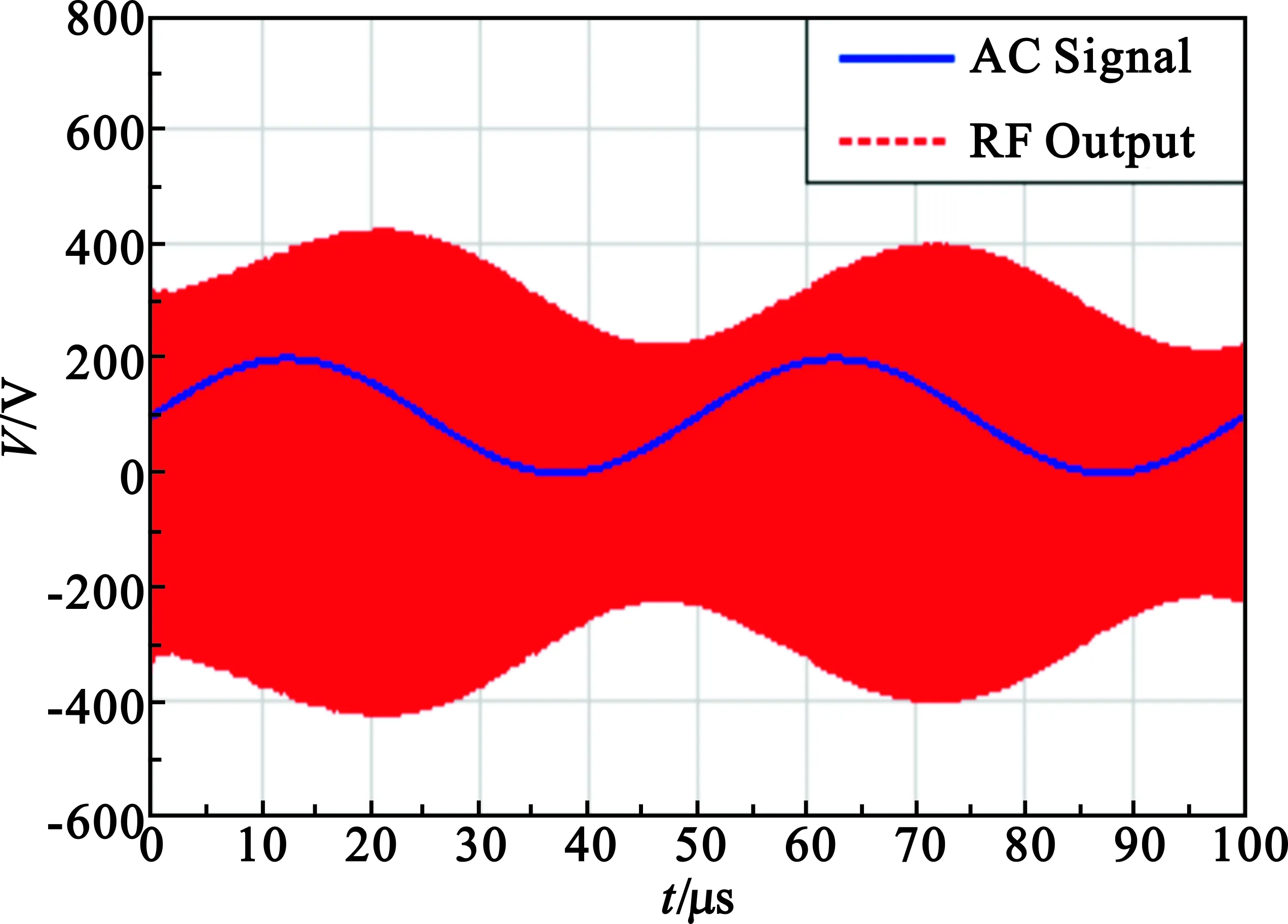
(a)Fac=20 kHz

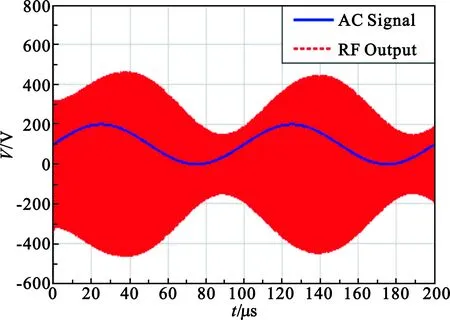
(b)Fac=10 kHz

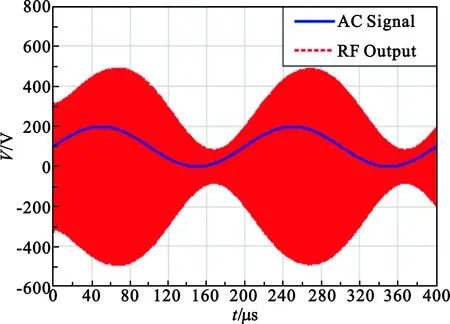
(c)Fac=5 kHz

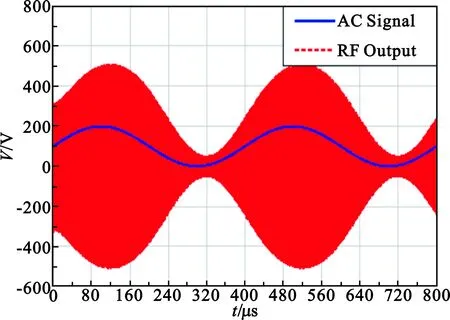
(d)Fac=2.5 kHz

由图4可知，对于kHz级别的交流信号，电调衰减器对其具有等效的相移的，在电调衰减器的射频输出中会得到体现。对于10 kHz，电调衰减器的等效相移可达到50°左右。而对于驱动电路，在不同控制电压Vdc下，其相移特性仿真曲线如图5所示。

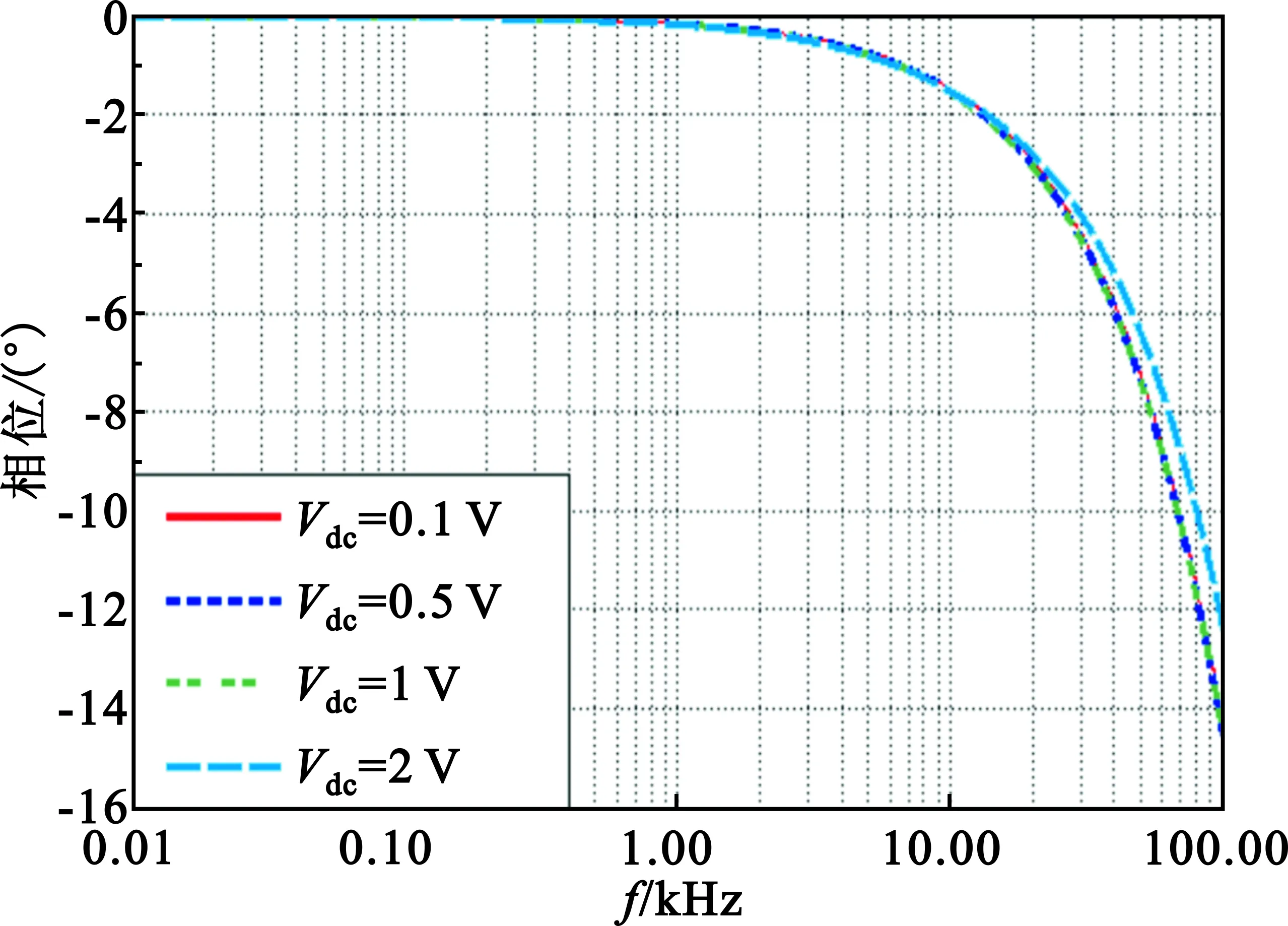
(a)正向电压相移仿真曲线

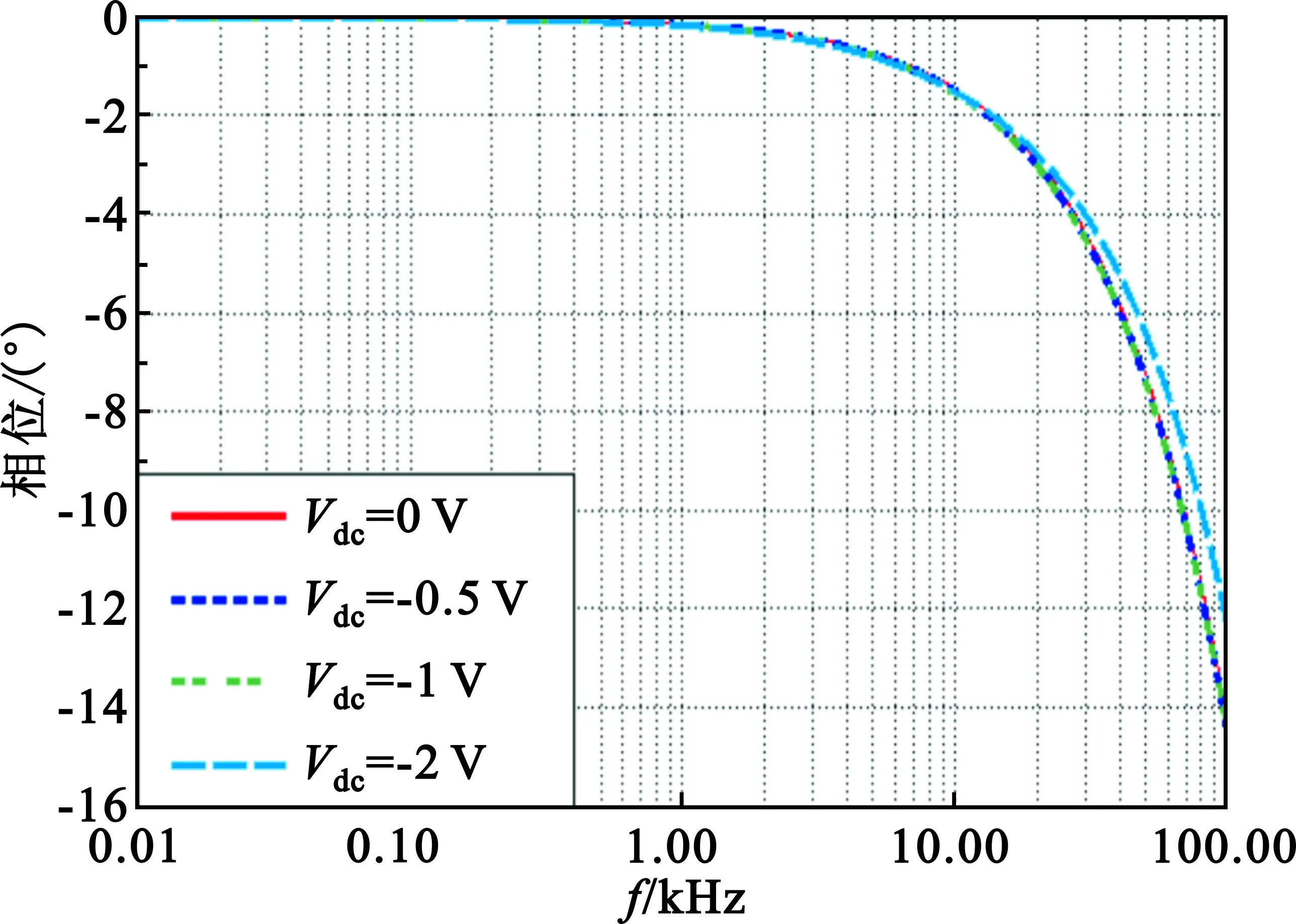
(b)反向电压相移仿真曲线

驱动电路在10 kHz以下的频段内带来的相移极小，因此可知，电调衰减器的衰减电路对控制信号中的交流分量的造成的等效相移影响较大。此相移足够大，对控制环路的稳定性会造成极大的影响。改变射频输入信号的功率及频率，控制信号中直流量以及交流量的幅值，不会影响到该相移。

5 试 验

5.1 电调衰减器响应时间测试

测试实际电调衰减的响应时间，图6所示的是射频输入信号功率为20 dBm、在控制电压由-2 V变为2 V时，射频输入信号的频率Fr下电调衰减器的瞬态特性。

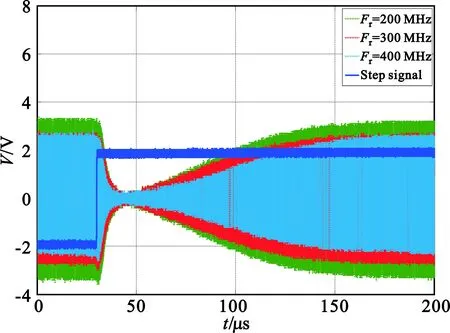
图6 不同输入功率条件下的电调衰减器瞬态特性Fig.6 Transient characteristics of electric adjustable attenuator under different input frequencies

实验结果也显示控制信号极性改变时，电调衰减器的响应时间可超过100 μs。通过实验测得电调衰减器对于一个阶跃信号，电调衰减器从一个稳定状态到另一个稳定状态所需的响应时间比仿真结果略长。这是由于对于实际电调而言，其桥臂所用的PIN二极管各参数不可能完全对称，桥臂的不平衡对其衰减特性有较大影响[14]，对其响应速度会造成影响。

5.2 反馈控制环路稳定性测试

通过前面仿真可知，电调衰减器的衰减电路会对控制信号中的交流分量具有较大等效相移。在此基础上搭建测试电路，如图7所示。由于驱动电路实际的相移很小，可认为电调衰减器衰减电路对于控制信号中交流分量的相移即为电调衰减器对于控制信号中交流分量的等效相移。选用300 MHz、20 dBm的射频输入信号，控制信号中直流量幅值为0.1 V，交流量幅值为0.05 V，改变交流信号的频率，选取一个周期观测，实验结果如图8所示。

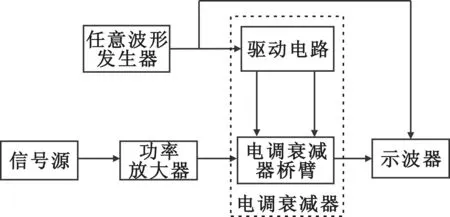
图7 电调衰减器衰减电路对控制信号中交流分量相移测试平台Fig.7 The platform for testing the influence on AC signal phase of attention circuit

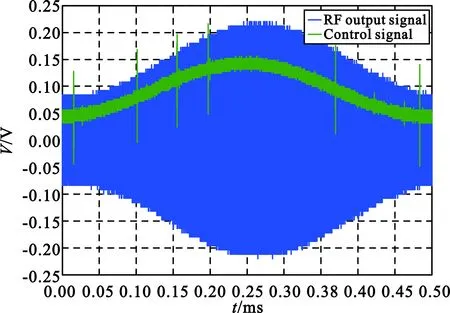
(a)Fac=2 kHz

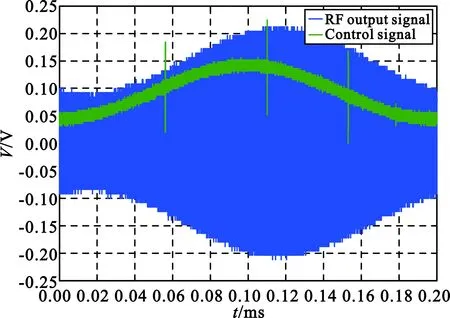
(b)Fac=5 kHz

(c)Fac=10 kHz图8 交流量频率对交流分量相移的影响Fig.8 The influence of AC signal frequency on AC signal phase

实验证实了电调衰减衰减电路对于控制信号中的交流信号具有等效相移，在10 kHz的相移约40°，且该相移与交流信号的频率有关。改变射频输入信号的功率及频率，控制信号中直流量以及交流量的幅值，不会影响到该相移。

对实际模拟对消装置进行测试，选取典型射频输入信号频率300 MHz，参考功率为30 dBm。当环路增益K=2 100时，通过改变时间常数τ，其对消速度关系变化如图9所示。由图9(a)可知，随着时间常数的增加，其对消速度变慢。对对消前后图像对比，如图9(b)所示，当系统时间常数较小时，在300 MHz处对消比基本无变化，但在300 MHz两侧有较高功率的峰值出现，系统发生环路振荡。

(a)不同时间常数对对消速度的影响

(b)不同时间常数对对消比的影响图9 时间常数与对消速度关系Fig.9 Relationship between time constant and cancellation speed

射频输入信号为300 MHz、参考功率为30 dBm，时间常数τ=0.9 s时，通过改变系统环路增益，其对消速度关系变化如图10(a)所示。随着环路增益的增加，其对消速度变快，且该频点对消后的功率更低。但是对对消前后图像对比，当环路增益K=2 700时，其对消后图像发生了振荡，在300 MHz两侧出现了较高功率的信号，如图10(b)所示。

(a)不同系统环路增益对对消速度的影响

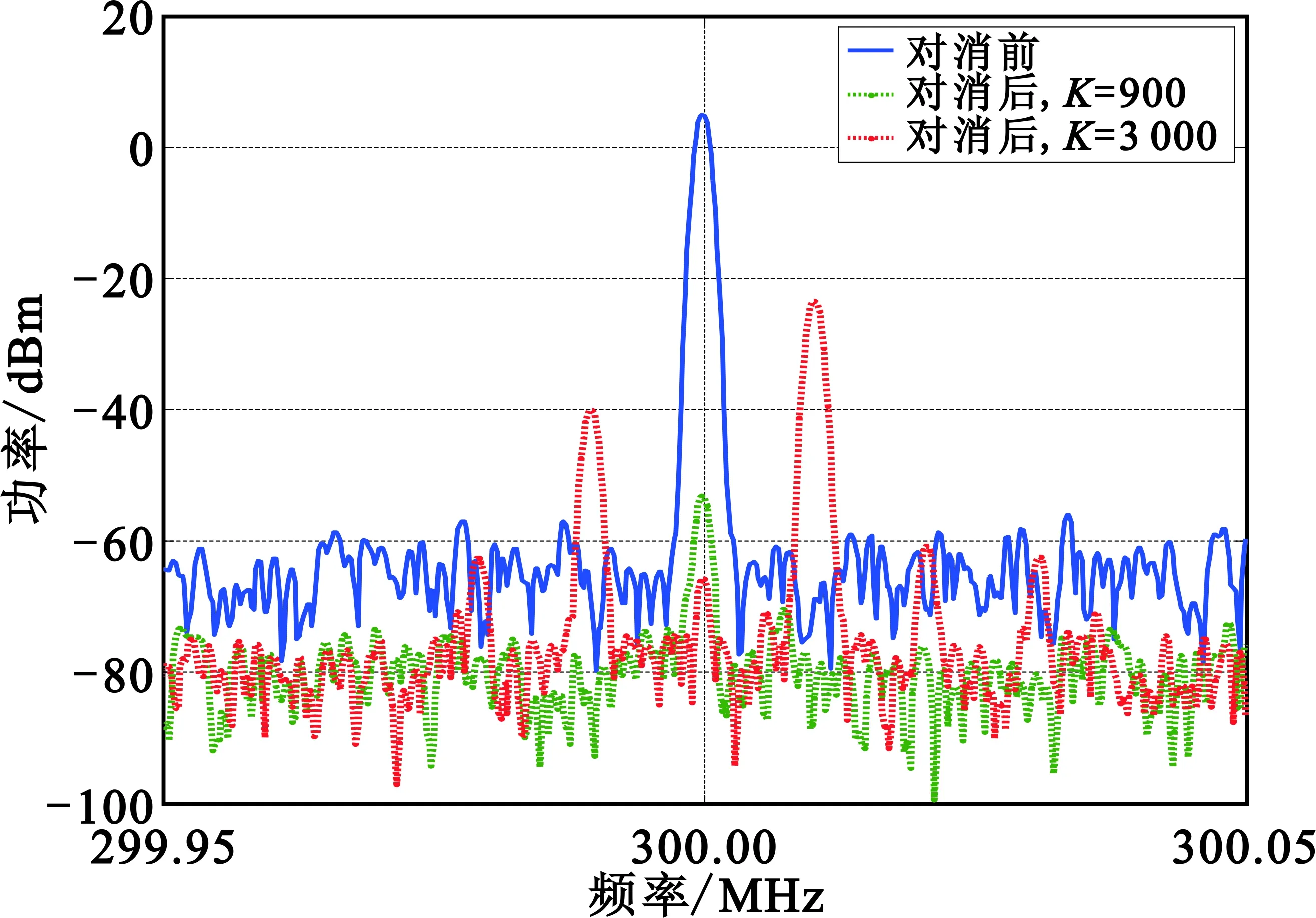
(b)不同系统环路增益对对消比的影响图10 系统环路增益与对消速度关系Fig.10 Relationship between system loop gain and cancellation speed

改变控制环路的环路增益以及时间常数会影响到系统的稳定裕度。由于控制环路中存在附加相移，通过前面的实验可知电调衰减衰减器电路对于控制信号中的交流分量具有等效相移，且在10 kHz的相移约为40°，在此条件下，对消系统的参数调整会受到系统稳定条件的限制，参数调整不合理将会引起系统振荡。

6 结束语

模拟自适应干扰对消系统对消速度的修正数学模型包含了对系统的稳定性以及电调衰减器射频响应特性的约束条件。电调衰减器的的响应时间超过100 μs，会对对消系统的对消速度造成较大影响。同时，由于电调衰减器衰减电路对于控制信号中交流分量的等效相移以及其余模拟器件的相移的累加，使得系统的稳定性受到影响，系统环路增益以及与系统时间常数的调整存在限制。修正模型对设计自适应干扰对消系统对消速度时的参数分配具有一定的指导意义，能够反映系统对消速度提升存在的制约条件。由于电调衰减器的衰减特性未能在模型中体现，对于计算最佳的兼顾对消比与对消速度的参数还存在难度。下一步可针对电调衰减器的衰减特性进一步修正对消速度模型，同时可结合系统的稳定裕度求解兼顾系统稳定裕度以及对消速度的数学模型。