结合全双工与协作干扰的无线网状网物理层安全策略*

(华南理工大学 电子与信息学院，广州510640)

1 引 言

传统的安全通信一般采用基于密码学的方法。物理层安全概念和窃听信道模型由Wyner在文献[1]中最先提出。物理层安全容量的大小由合法信道和窃听者信道之间的信道容量差决定。增强物理层安全的基本手段是提高合法用户间信道的质量，同时劣化窃听者接收信号的信道环境。

无线网状网有广泛的应用，目前已有文献专门研究协作中继通信中的物理层安全问题[2-4]，但物理层安全的方法都是基于半双工(Half-duplex,HD)的。近年来先进的自干扰消除技术的出现，使得同时同频全双工(Full-duplex,FD)传输方式吸引了大量的关注[5-8]。引入人工干扰降低窃听者解码能力的方案是目前提升物理层安全的主要手段之一[9-13]。

从相关工作可以看到，有关通过FD或协作干扰方法提升物理层安全性能的问题已经被人们关注。一方面，FD使接收节点在接收信号同时发射干扰信号，以提高保密性能；另一方面，加入协作干扰可以有效劣化窃听者信道环境，增强安全性能。但现有的基于FD或基于协作干扰的物理层安全方法大多假定窃听者的位置已知或窃听信道特性已知，因而具有很大的局限性。另外，现有的物理层安全方法很难同时对付潜在接收节点附近及远处的窃听者，如果只采用FD自干扰措施保护接收节点附近区域，则无法对抗可能潜伏在信号可达的较远位置的窃听者，此时窃听者之间可能通过协作从弱信号中获取信息；若仅考虑协作干扰技术保证信息传输安全，接收节点可能会受到位于其附近的协作节点发送的协作干扰信号的较大干扰。

针对上述问题，本文提出了一种在无线网状网中基于FD和协作干扰技术的增强物理层安全性能的方法，导出了在该方案下任意给定路径的安全连接概率(Secure Connection Probability,SCP)计算表达式。实验仿真结果验证了所得结果的合理性。与一般的无线网状网相比，所提方法可使网络安全性能显著提升。

2 系统模型

本文研究的无线网状网场景如图1所示，系统中包含了合法节点和窃听者两类节点。合法节点间的相对位置已知，而潜伏窃听者位置不可知。记任一传输路径的合法节点集合为{An|n=1,2,…,N}，其中A1为源节点，AN为目的节点，其他为中继节点，N表示该路径合法节点数，路径中的每一个节点An仅可接收来自路径中前一节点An-1的信息，所有中继均采用随机转发(Random-and-Forward,RaF)策略。根据已知传输路径节点相对位置及需保护的范围，选择网络中不参与信息传输的部分合法节点组成协作节点集合{Cm|m=1,2,…,M}发送干扰信号，其中M表示选取的协作节点数。对位于可能窃取信息位置的潜在窃听者进行干扰，因为协作干扰信号也可能会对信息传输路径上的接收节点(包含中继节点和目的节点)正常接收信号造成干扰，因此接收节点附近不能采用简单协作干扰的方式。本文采取的策略是：在信号可达范围且远离接收节点的位置，通过协作干扰对信息进行保护；而在接收节点附近，则通过接收节点自身发送的干扰对信息进行保护，接收节点可利用同时同频全双工技术中可有效抑制自发信号干扰的特点消除对自身接收信号的干扰，而对潜在窃听者面对的则是难以消除的随机干扰，由此可获得安全容量的提高。

图1 基于FD和协作干扰的物理层安全信息传输模型示意图Fig.1 The model diagram of physical layer security information transmission based on full-duplex and cooperative jamming

已知An与An+1节点间的距离dAnAn+1，假设An发送的信号的传输距离为dAnAn+1，即An+1处接收到的信号功率为接收端所需的最小接收功率Pt,在实际系统中，该值可根据采用的调制编码方式所需的信噪比决定。如果只考虑大尺度衰落，根据dAnAn+1可确定An发送信的功率，即取

P=Pt|D|α。

式中：P为发送功率；|D|-α是路损衰落，D为距离，α为路径损耗指数。接收节点An+1附近的区域由其自身发送同时同频的干扰信号提供安全保证，An+1自发干扰信号功率大小与其向下一接收节点发送信号功率一致。一般来说采用尽可能多的协作干扰节点，总是有利于降低窃听者的信干噪比，理论上位于发送信号覆盖范围以外的窃听者难以获得任何信息。综合考虑能效和复杂性等因素，以每个发送节点An为中心、2dAnAn+1为半径的圆内的其他合法节点可选为协作节点。上述节点中可能存在距离各个An+1较近的节点，其发送的协作干扰信号对An+1接收信号产生较大的干扰，又因An+1附近区域已通过自干扰获得较好保护，自干扰覆盖范围内的合法节点不参与协作。为避免协作干扰信号对各个An+1接收信号造成明显干扰，协作干扰信号的传输距离dCm应小于Cm与{An|n=2,3,…,N}间距离的最小值v=min(dCmAn)，取dCm=v-Δ，其中Δ是一干扰调整量，通过控制Δ取值的大小可以调整协作干扰信号的覆盖范围，取值过小会使协作节点发送的干扰信号对接收节点接收信号带来较严重的干扰，取值过大则将使协作干扰信号的保护范围减小，这都会使SCP降低。根据dCm由式P=Pt|D|α确定协作干扰信号的功率。

综上，本文所讨论的方法中有关协作节点选择及相关参数确定的算法(算法1)可归纳如下。

输入：网络中合法节点的位置信息以及网络拓扑结构；源节点A1与目的节点AN。

输出：

Step1 由源节点A1与目的节点AN，根据迪杰斯特拉(Dijkstra)算法确定传输路径和相应的节点集{An|n=2,3,…,N}；

Step2 确定发送节点An的信号发送功率；

Step3 根据Step 2中得到的功率值确定接收节点An+1发送自干扰信号功率；

Step4 在以每个发送节点An为中心、2dAnAn+1为半径的圆内区域选择协作干扰节点；

Step5 在Step 4中确定的区域内，除去存在于自干扰保护区域的协作节点；

Step6 确定协作干扰保护范围，得到协作节点Cm发送协作干扰信号功率取值。

算法的相应流程如图2表示。

图2 协作节点选择及相关参数确定算法流程图Fig.2 The flow chart for the algorithm of jammers selection and related parameters determination

由此可以确定所选传输路径、协作节点以及各个节点的发送信号功率。

假定合法节点的密度为λ，合法节点具有同时同频全双工的能力，合法节点间的拓扑结构和相互间距离已知。窃听者为齐次泊松点过程(Poisson Point Process,PPP)分布[8]，位置未知，其密度为λe。考虑最不利的情况，假定窃听者间可协作。信道中的噪声设为零均值单位方差的加性高斯白噪声(Additive White Gaussian Noise,AWGN)。由此，An+1接收An发送信号的信干噪比和任一窃听者el接收An发送信号的信干噪比可以分别表示为

(1)

(2)

根据文献[15]，从An到An+1的单跳传输链路的安全速率为

[lb(1+SINRn+1)-lb(1+SINRen)]+。

(3)

式中：[x]+=max(x,0)；SINRen表示节点An发送信号时，窃听者集合Φe中各个窃听者的信干燥比。本文假设窃听者间可协作，潜伏在不同位置的窃听者可将各自窃听到的信息重新组合，获得协作分集的增益。从通信安全角度看，这是一种最不利的场景。根据最大比合并(Maximal-Ratio Combiner,MRC)算法，SINRen可表示为各个窃听者所得信号的信干噪比之和[4]，即

(4)

因为潜在的窃听者位置不知，无法得到其信道状态信息(Channel State Information,CSI)，一般只能采用SCP来描述传输路径的安全特性。采用文献[15]中关于安全连接的定义，如果在某条已选定的路径上，安全速率大于零，则该路径安全。由于所有中继均采用RaF策略，路径上的每一跳之间均相互独立，因此需要保证每一跳的安全速率均为正，即应有

lb(1+SINRn+1)-lb(1+SINRen)>0,n=1,2,…,N-1 。

(5)

由上可得，对于一条给定路径，第n跳的SCP可以表示为

SCPn=P[lb(1+SINRn+1)-lb(1+SINRen)>0] 。

(6)

因此，路径的SCP为

(7)

3 基于全双工和协作干扰的物理层安全

本节首先分析任意给定两节点间的SCP,一般的有如下的引理。

引理1 若X是均值为1的独立指数分布随机变量，且A、B、C均为正数，则有

(8)

(9)

因篇幅有限，引理的证明略。

另外，若Y是均值为1的独立指数分布随机变量，由文献[8]可得

(10)

将式(1)～(2)代入式(6)，可以得到

(11)

对于指数分布随机变量X，其分布函数为

P(X>x)=exp(-λx)。

(12)

(13)

(14)

式中：

根据文献[16]，有以下不等式：

(15)

(16)

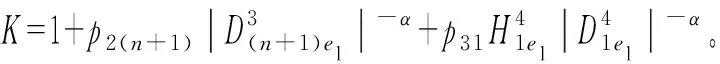
(17)

式中：

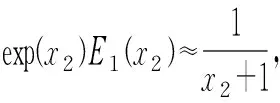
(18)

(19)

式中：

(20)

根据文献[17]，齐次PPP的概率母泛函(Probability Generating Functional,PGFL)可以表示为

(21)

因此，式(20)可以整理为

(22)

当使用一个以上协作节点时，通过采取与上述使用一个协作节点时相同的推导方法，可以得到当采用M个协作节点对窃听者进行干扰时，SCP的一般表达式为

(23)

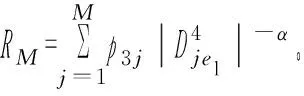
由于采用多跳随机转发中继传输方式，每一跳的过程均为相互独立，根据式(7)，可以导出采用M个协作节点时，对于整个传输过程的SCP表达式可以表示为

(24)

由于窃听者可能位于网络中的任意位置，窃听者与任一合法节点间的距离在统计平均意义上是相等的，在这样的假设下，可将式(24)整理为

(25)

式中：Γ函数虽不是严格意义上的闭合表达式，但利用计算机可以很方便地计算其数值。在下一节中，蒙特卡洛仿真结果表明式(25)与仿真结果有很好的符合性。

4 数值仿真和性能分析

仿真设定在2 000×2 000大小的网络区域中，随机产生密度为10-2的合法节点，即节点间的平均距离为10，取α=4、η=0.2。实验表明取干扰调整量为平均距离的20%时有较好的折中结果，因此仿真中取Δ=2。仿真中每个场景针对按照PPP随机分布的不同窃听者密度即单位面积的窃听者数(10-5～10-2)，分别进行10 000次蒙特卡洛仿真，对仿真数据求取统计平均值获得仿真结果。图3给出的是仿真过程中的一个实例。

图3 研究场景节点位置图Fig.3 The position of nodes in the study scenario

图4比较了结合FD和协作干扰时的蒙特卡洛仿真与仅依赖FD自干扰或协作干扰情况下的蒙特卡洛仿真结果。通过结果可以发现，在FD自干扰和协作干扰结合的情况下，相比仅依赖FD自干扰或协作干扰的方式，SCP获得较为显著的提升，尤其是窃听者密度在10-4～5×10-3时，这个提升更为明显，有利于保证可靠的信息安全传输。但当窃听者密度增大到10-2时，即与合法节点密度相同时，SCP将接近0，显然此时已经不可能实现安全连接。此外还可发现，在相同场景下，信息传输经过的跳数N越多，3种方法下的SCP均将变得越来越小，同时提出的方法获得的性能提升也将逐渐减弱，这是由于在跳数增加时，协作的窃听者可以通过组合在每跳中窃取的信号获取更多的信息，对抗各项干扰，从而导致安全性下降。

图4 结合FD和协作干扰、仅FD、仅协作干扰情况下的蒙特卡洛仿真结果对比Fig.4 Monte Carlo simulation results of scenarios combining FD and cooperative jamming,with FD,and with cooperative jamming

图5 同一场景下蒙特卡洛仿真结果和SCP近似表达式的结果对比Fig.5 Comparison between the Monte Carlo simulation result and SCP approximation in the same scenario

5 结束语

本文提出了一种无线网状网中基于FD和协作干扰的一种有效提升物理层安全性能的方法。在存在随机分布且位置未知窃听者的无线网状网中，每个信息传输中继节点在接收信号时采用FD方式干扰窃听者，并通过自干扰消除技术来降低FD方式对接收到信号的影响,同时结合协作干扰技术，通过协作干扰信号有效劣化窃听者信道环境。与仅采用FD或协作干扰情况下的物理层安全方法性能进行比较与分析，仿真结果表明基于全双工和协作干扰的方法可有效提高无线网状网中的信息传输安全性能。对该场景下任意给定路径的SCP进行了分析并导出了近似表达式，且通过实验仿真结果验证了表达式的合理性。本课题将进一步研究网络动态变化以及传输跳数增加时如何获得现有安全性能的提升等问题。